2.4: Adición de vectores complejos
- Page ID
- 153474
Si se agregan vectores con ángulos poco comunes, sus magnitudes (longitudes) se suman de manera bastante diferente a la de las magnitudes escalares: (Figura a continuación)
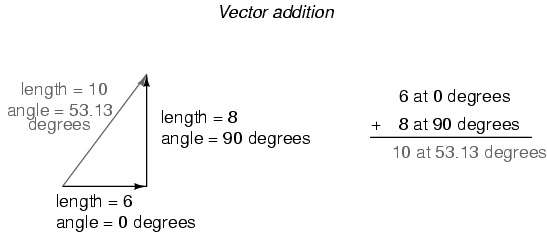
Las magnitudes vectoriales no se suman directamente para ángulos desiguales.
Si dos voltajes de CA, 90 o fuera de fase, se suman al estar conectados en serie, sus magnitudes de voltaje no suman ni restan directamente como ocurre con los voltajes escalares en CC. En cambio, estas cantidades de voltaje son cantidades complejas, y al igual que los vectores anteriores, que se suman de manera trigonométrica, una fuente de 6 voltios a 0 o añadida a una fuente de 8 voltios a 90 o da como resultado 10 voltios en un ángulo de fase de 53.13 o: (Figura a continuación)
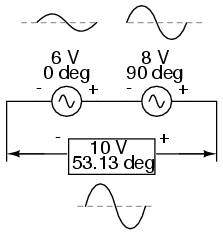
Las fuentes de 6V y 8V se suman a 10V con la ayuda de la trigonometría.
En comparación con el análisis de circuitos de CC, esto es realmente muy extraño. Tenga en cuenta que es posible obtener indicaciones de voltímetro de 6 y 8 voltios, respectivamente, a través de las dos fuentes de voltaje de CA, ¡pero solo se leen 10 voltios para un voltaje total!
No hay una analogía de CC adecuada para lo que estamos viendo aquí con dos voltajes de CA ligeramente desfasados. Los voltajes de CC solo pueden ayudar directamente o oponerse directamente, sin nada en el medio. Con CA, dos voltajes pueden ayudar u oponerse entre sí en cualquier grado entre totalmente auxiliar y completamente opuesto, inclusive. Sin el uso de notación vectorial (número complejo) para describir las cantidades de CA, sería muy difícil realizar cálculos matemáticos para el análisis de circuitos de CA.
En la siguiente sección, aprenderemos a representar cantidades vectoriales en forma simbólica en lugar de gráfica. Los diagramas vectoriales y triangulares bastan para ilustrar el concepto general, pero se deben utilizar métodos más precisos de simbolismo si se quiere realizar algún cálculo serio sobre estas cantidades.
Revisar
Los voltajes de CC solo pueden ayudar directamente o oponerse directamente entre sí cuando se conectan en serie. Los voltajes de CA pueden ayudar u oponerse en cualquier grado dependiendo del desplazamiento de fase entre ellos.


