8.5: Efectos de circuito
- Page ID
- 153280
El principio de formas de onda no sinusoidales, repetitivas que son equivalentes a una serie de ondas sinusoidales a diferentes frecuencias es una propiedad fundamental de las ondas en general y tiene gran importancia práctica en el estudio de los circuitos de CA. Significa que cada vez que tenemos una forma de onda que no es perfectamente en forma de onda sinusoidal, el circuito en cuestión reaccionará como si tuviera una matriz de diferentes voltajes de frecuencia impuestos sobre él a la vez.
Cuando un circuito de CA se somete a una tensión de fuente que consiste en una mezcla de frecuencias, los componentes en ese circuito responden a cada frecuencia constituyente de una manera diferente. Cualquier componente reactivo, como un condensador o un inductor, presentará simultáneamente una cantidad única de impedancia para todas y cada una de las frecuencias presentes en un circuito. Agradecidamente, el análisis de tales circuitos se hace relativamente fácil aplicando el Teorema de Superposición, considerando la fuente de frecuencia múltiple como un conjunto de fuentes de voltaje de frecuencia única conectadas en serie, y analizando el circuito para una fuente a la vez, sumando los resultados al final a determinar el total agregado:
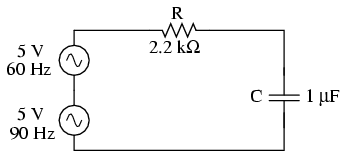
Circuito accionado por una combinación de frecuencias: 60 Hz y 90 Hz.
Circuito de análisis solo para fuente de 60 Hz:
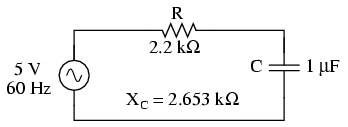
Circuito para resolver 60 Hz.
Analizando el circuito solo para la fuente de 90 Hz:
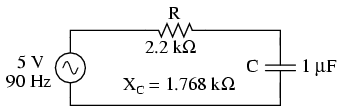
Circuito de resolución de 90 Hz.
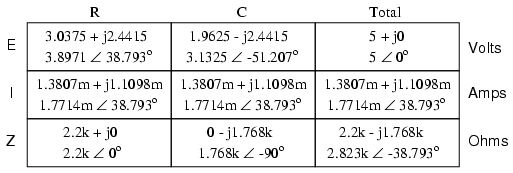
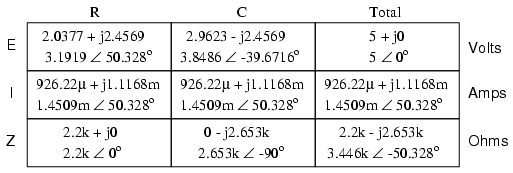
Superponiendo las caídas de voltaje a través de R y C, obtenemos:
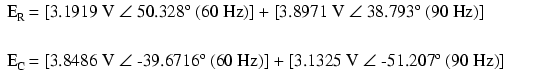
Debido a que los dos voltajes a través de cada componente están a frecuencias diferentes, no podemos consolidarlos en una sola cifra de voltaje como podríamos si estuviéramos sumando dos voltajes de diferente amplitud y/o ángulo de fase a la misma frecuencia. La notación numérica compleja nos da la capacidad de representar la amplitud de la forma de onda (magnitud polar) y el ángulo de fase (ángulo polar), pero no la frecuencia.
Lo que podemos decir de esta aplicación del teorema de superposición es que habrá una caída de voltaje mayor de 60 Hz a través del condensador que una tensión de 90 Hz. Justo lo contrario es cierto para la caída de voltaje de la resistencia. Esto es digno de mención, sobre todo a la luz de que los dos voltajes de fuente son iguales. Es este tipo de respuesta de circuito desigual a señales de diferente frecuencia lo que será nuestro enfoque específico en el próximo capítulo.
También podemos aplicar el teorema de superposición al análisis de un circuito alimentado por una tensión no sinusoidal, como una onda cuadrada. Si conocemos la serie de Fourier (equivalente de onda sinusoidal múltiple) de esa onda, podemos considerarla como originaria de una cadena conectada en serie de múltiples fuentes de voltaje sinusoidales a las amplitudes, frecuencias y desplazamientos de fase apropiados. No hace falta decir que esto puede ser una tarea laboriosa para algunas formas de onda (se considera que una serie precisa de Fourier de onda cuadrada se expresa al noveno armónico, ¡o cinco ondas sinusoidales en total!) , pero es posible. Menciono esto no para asustarte, sino para informarte de la complejidad potencial que acecha detrás de formas de onda aparentemente simples. Un circuito de la vida real responderá de la misma manera a ser alimentado por una onda cuadrada que a ser alimentado por una serie infinita de ondas sinusoidales de frecuencias impares múltiples y amplitudes decrecientes. Se sabe que esto se traduce en resonancias inesperadas del circuito, sobrecalentamiento del núcleo del transformador e inductor debido a corrientes parásitas, ruido electromagnético en amplios rangos del espectro de frecuencia y similares. Los técnicos e ingenieros deben ser conscientes de los efectos potenciales de las formas de onda no sinusoidales en los circuitos reactivos.
También se sabe que los armónicos manifiestan sus efectos en forma de radiación electromagnética. Se han realizado estudios sobre los peligros potenciales del uso de computadoras portátiles a bordo de aviones de pasajeros, citando el hecho de que las señales de voltaje de “reloj” de onda cuadrada de alta frecuencia de las computadoras son capaces de generar ondas de radio que podrían interferir con el funcionamiento de la navegación electrónica de la aeronave equipo. Ya es bastante malo que las frecuencias típicas de la señal de reloj del microprocesador estén dentro del rango de las bandas de radiofrecuencia de los aviones, pero peor aún es el hecho de que los múltiplos armónicos de esas frecuencias fundamentales abarcan un rango aún mayor, debido a que los voltajes de la señal de reloj son de onda cuadrada en forma y no onda sinusoidal.
Las “emisiones” electromagnéticas de esta naturaleza también pueden ser un problema en aplicaciones industriales, ya que los armónicos abundan en cantidades muy grandes debido al control electrónico (no lineal) de la potencia del motor y del horno eléctrico. La frecuencia fundamental de la línea eléctrica puede ser solo de 60 Hz, pero esos múltiplos de frecuencia armónicos teóricamente se extienden en rangos de frecuencia infinitamente altos. El voltaje y la corriente de la línea eléctrica de baja frecuencia no irradian al espacio muy bien como la energía electromagnética, pero las frecuencias altas sí.
Además, el “acoplamiento” capacitivo e inductivo causado por conductores de proximidad cercana suele ser más severo a altas frecuencias. El cableado de señal cercano al cableado de alimentación tenderá a “captar” la interferencia armónica del cableado de alimentación en un grado mucho mayor que la interferencia pura de ondas sinusoidales. Este problema puede manifestarse en la industria cuando los viejos controles de motor son reemplazados por nuevos controles electrónicos de motor de estado sólido que proporcionan una mayor eficiencia energética. De repente, puede haber un ruido eléctrico extraño que se impresiona en el cableado de la señal que nunca solía estar allí, porque los viejos controles nunca generaban armónicos, y esos voltajes y corrientes armónicos de alta frecuencia tienden a “acoplarse” inductiva y capacitivamente mejor a los conductores cercanos que cualquier señal de 60 Hz de los controles antiguos acostumbrados a.
Revisar
- Cualquier forma de onda regular (repetitiva), no sinusoidal es equivalente a una serie particular de ondas senoidales de diferentes frecuencias, fases y amplitudes, más un voltaje de compensación de CC si es necesario. El proceso matemático para determinar la forma de onda sinusoidal equivalente para cualquier forma de onda se denomina análisis de Fourier.
- Las fuentes de voltaje de frecuencia múltiple se pueden simular para su análisis conectando varias fuentes de voltaje de frecuencia única en serie. El análisis de voltajes y corrientes se realiza utilizando el teorema de superposición. NOTA: no se pueden sumar tensiones y corrientes superpuestas de diferentes frecuencias en forma de número complejo, ya que los números complejos solo dan cuenta de amplitud y desplazamiento de fase, ¡no de frecuencia!
- Los armónicos pueden causar problemas al impresionar señales de voltaje no deseadas (“ruido”) en circuitos cercanos. Estas señales no deseadas pueden venir por medio de acoplamiento capacitivo, acoplamiento inductivo, radiación electromagnética o una combinación de los mismos.


