1.3: Pitágoras
- Page ID
- 151435
¿Quién es este Pitágoras y por qué le importa?
Pitágoras fue un filósofo griego que vivió alrededor del 500 a.C. Se le atribuye como filósofo y matemático. Gran parte de lo que sabemos de Pitágoras es de escritos que fueron copiados cientos de años después de su muerte, por lo que la validez de lo que sí sabemos es cuestionable. Se le atribuye el teorema de Pitágoras cuando en realidad se ha demostrado que babilonios e indios estaban usando variaciones del mismo durante cientos de años antes incluso de que él llegara. Se puede encontrar más sobre él en este artículo.
Gracias por la lección de historia, ¡pero sigue adelante con ella!
El teorema de Pitágoras, también conocido como teorema de Pitágoras, es una relación en la geometría euclidiana entre los tres lados de un triángulo rectángulo. 'Afirma que el cuadrado de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de los otros dos lados.
No es tan malo como parece. Básicamente, el teorema de Pitágoras dice que puedes averiguar cualquier lado de un triángulo rectángulo siempre y cuando tengas los otros dos lados, usando la ecuación:
\[A^2 + B^2 = C^2\]
Cuando miramos la fórmula, hay una cosa importante para recordar: siempre\(C\) es el lado más largo. \(A\)y\(B\) puede intercambiarse alrededor, pero al usar esta fórmula, siempre\(C\) es el lado más largo (que también es el lado opuesto al ángulo de 90 grados).
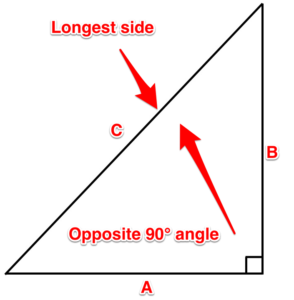
Figura 15. Triángulo lateral más largo
¡Video! Este video explica cómo aplicar el teorema de Pitágoras en un triángulo rectángulo.


