1.6: Básculas absolutas en dB
- Page ID
- 153682
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Un sonido que mide 40 dB en la escala sonora de decibelios sería 10 4 veces mayor que el umbral de audición. Un sonido de 100 dB sería 10 10 (diez mil millones) veces mayor que el umbral de audición.
Debido a que el oído humano no es igualmente sensible a todas las frecuencias de sonido, se han desarrollado variaciones de la escala de potencia sonora de decibelios para representar intensidades de sonido fisiológicamente equivalentes a diferentes frecuencias. Algunos instrumentos de intensidad sonora fueron equipados con redes de filtro para dar indicaciones desproporcionadas a través de la escala de frecuencia, cuya intención de representar mejor los efectos del sonido en el cuerpo humano. Tres escalas filtradas se conocían comúnmente como las escalas ponderadas “A”, “B” y “C”. Las indicaciones de intensidad sonora de decibelios medidas a través de estas respectivas redes de filtrado se dieron en unidades de dBA, dBb y dBc. Hoy en día, la “escala ponderada A” se usa más comúnmente para expresar el impacto fisiológico equivalente en el cuerpo humano, y es especialmente útil para calificar fuentes de ruido peligrosamente fuertes.
Se ha establecido otro sistema normalizado de medición de potencia en la unidad de decibelios para su uso en sistemas de telecomunicaciones. A esto se le llama la escala dBm. (Figura a continuación) El punto de referencia, 0 dBm, se define como 1 milivatio de energía eléctrica disipada por una carga de 600 Ω. Según esta escala, 10 dBm es igual a 10 veces la potencia de referencia, o 10 milivatios; 20 dBm es igual a 100 veces la potencia de referencia, o 100 milivatios. Algunos voltímetros de CA vienen equipados con un rango o escala de dBm (a veces etiquetado como “DB”) destinado a su uso en la medición de la potencia de la señal de CA a través de una carga de 600 Ω. 0 dBm en esta escala es, por supuesto, elevado por encima de cero porque representa algo mayor que 0 (en realidad, representa 0.7746 voltios a través de una carga de 600 Ω, siendo igual a la raíz cuadrada de potencia por resistencia; la raíz cuadrada de 0.001 multiplicada por 600). Cuando se ve en la cara de un movimiento de medidor analógico, esta escala de dBm aparece comprimida en el lado izquierdo y expandida a la derecha de una manera no diferente a una escala de resistencia, debido a su naturaleza logarítmica.
Las mediciones de potencia de radiofrecuencia para señales de bajo nivel encontradas en receptores de radio utilizan mediciones de dBm referidas a una carga de 50 Ω. Los generadores de señal para la evaluación de receptores de radio pueden emitir una señal nominal dBm ajustable. El nivel de señal es seleccionado por un dispositivo llamado atenuador, descrito en la siguiente sección.
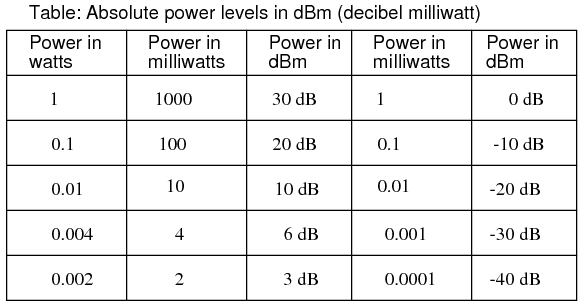
Niveles de potencia absoluta en dBm (decibelios referenciados a 1 milivatio).
Una adaptación de la escala dBm para la intensidad de la señal de audio se utiliza en la ingeniería de grabación de estudio y broadcast para estandarizar los niveles de volumen, y se denomina escala VU. Los medidores VU se ven frecuentemente en los instrumentos de grabación electrónica para indicar si la señal grabada excede o no el límite de nivel máximo de señal del dispositivo, donde se producirá una distorsión significativa. Esta escala de “indicador de volumen” se calibra de acuerdo con la escala de dBm, pero no indica directamente dBm para ninguna señal que no sean tonos de onda sinusoidal constante. La unidad de medida adecuada para un medidor de VU son las unidades de volumen.
Cuando se tratan señales relativamente grandes, y una escala de dB absoluta sería útil para representar el nivel de señal, a veces se utilizan escalas de decibelios especializadas con puntos de referencia mayores que el 1 mW utilizado en dBm. Tal es el caso de la escala dBW, con un punto de referencia de 0 dBW establecido en 1 Watt. Otra medida absoluta de potencia llamada escala dBk hace referencia a 0 dBk a 1 kW, o 1000 Watts.
Revisar
- La unidad del bel o decibelio también se puede usar para representar una medición absoluta de la potencia en lugar de solo una ganancia o pérdida relativa. Para las mediciones de potencia sonora, 0 dB se define como un punto de referencia estandarizado de potencia igual a 1 picovatio por metro cuadrado. Otra escala de dB adecuada para mediciones de intensidad de sonido se normaliza a los mismos efectos fisiológicos que un tono de 1000 Hz, y se llama escala dBA. En este sistema, 0 dBA se define como cualquier sonido de frecuencia que tenga la misma equivalencia fisiológica que un tono de 1 picovatio-pormetro cuadrado a 1000 Hz.
- Se ha realizado una escala eléctrica dB con un punto de referencia absoluto para su uso en sistemas de telecomunicaciones. Llamada escala dBm, su punto de referencia de 0 dBm se define como 1 milivatio de potencia de señal de CA disipada por una carga de 600 Ω.
- Un medidor de VU lee el nivel de señal de audio de acuerdo con el dBm para señales de onda sinusoidal. Debido a que su respuesta a señales distintas a las ondas sinusoidales constantes no es lo mismo que el dBm verdadero, su unidad de medida son las unidades de volumen.
- Las escalas dB con puntos de referencia absolutos mayores que la escala dBm se han inventado para señales de alta potencia. La escala dBW tiene su punto de referencia de 0 dBW definido como 1 Watt de potencia. La báscula dBk establece 1 kW (1000 Watts) como referencia de punto cero.


