Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

7.3: Identidades algebraicas booleanas

Última actualización

31 oct 2022
Guardar como PDF
- 7.2: Aritmética booleana
- 7.4: Propiedades algebraicas booleanas

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

En matemáticas, una identidad es una afirmación verdadera para todos los valores posibles de su variable o variables. La identidad algebraica de x + 0 = x nos dice que cualquier cosa (x) agregada a cero es igual a la “cualquier cosa” original, sin importar qué valor pueda ser esa “cualquier cosa” (x). Al igual que el álgebra ordinaria, el álgebra booleana tiene sus propias identidades únicas basadas en los estados bivalentes de las variables booleanas.

La primera identidad booleana es que la suma de cualquier cosa y cero es la misma que la “cualquier cosa” original. Esta identidad no es diferente de su equivalente algebraico de número real:

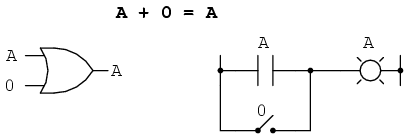
No importa cuál sea el valor de A, la salida siempre será la misma: cuando A=1, la salida también será 1; cuando A=0, la salida también será 0.

La siguiente identidad es definitivamente diferente de cualquier vista en álgebra normal. Aquí descubrimos que la suma de cualquier cosa y uno es uno:

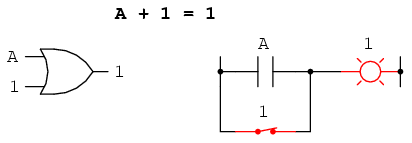
No importa cuál sea el valor de A, la suma de A y 1 siempre será 1. En cierto sentido, la señal “1” anula el efecto de A en el circuito lógico, dejando la salida fija en un nivel lógico de 1.

A continuación, examinamos el efecto de sumar A y A juntos, que es lo mismo que conectar ambas entradas de una puerta OR entre sí y activarlas con la misma señal:

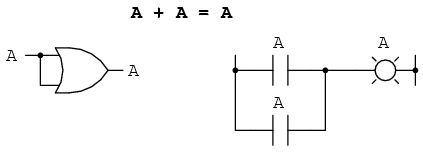
En el álgebra de números reales, la suma de dos variables idénticas es el doble del valor de la variable original (x + x = 2x), pero recuerde que no hay concepto de “2” en el mundo de las matemáticas booleanas, solo 1 y 0, por lo que no podemos decir que A + A = 2A. Así, cuando agregamos una cantidad booleana a sí mismo, la suma es igual a la cantidad original: 0 + 0 = 0, y 1 + 1 = 1.

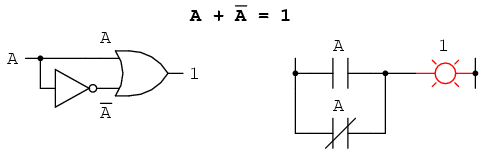
Introduciendo el concepto booleano único de complementación en una identidad aditiva, encontramos un efecto interesante. Dado que debe haber un valor “1” entre cualquier variable y su complemento, y dado que la suma de cualquier cantidad booleana y 1 es 1, la suma de una variable y su complemento debe ser 1:

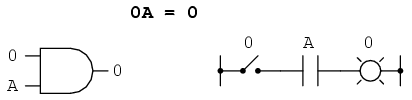
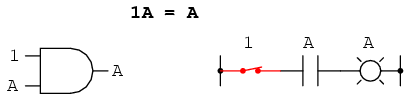
Así como hay cuatro identidades aditivas booleanas (A+0, A+1, A+A y A+A'), también hay cuatro identidades multiplicativas: Ax0, Ax1, AxA y Axa'. De estos, los dos primeros no son diferentes de sus expresiones equivalentes en álgebra regular:

La tercera identidad multiplicativa expresa el resultado de una cantidad booleana multiplicada por sí misma. En álgebra normal, el producto de una variable y en sí mismo es el cuadrado de esa variable (3 x 3 = 3 ² = 9). No obstante, el concepto de “cuadrado” implica una cantidad de 2, que no tiene significado en álgebra booleana, por lo que no podemos decir que A x A = A ². En cambio, encontramos que el producto de una cantidad booleana y en sí misma es la cantidad original, ya que 0 x 0 = 0 y 1 x 1 = 1:

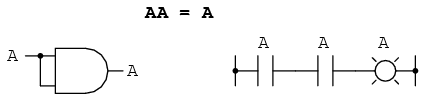
La cuarta identidad multiplicativa no tiene equivalente en álgebra regular porque utiliza el complemento de una variable, concepto único de las matemáticas booleanas. Dado que debe haber un valor “0” entre cualquier variable y su complemento, y como el producto de cualquier cantidad booleana y 0 es 0, el producto de una variable y su complemento debe ser 0:

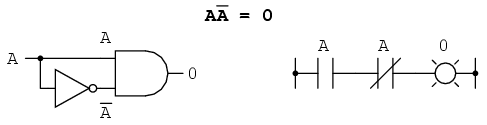
Para resumir, entonces, tenemos cuatro identidades booleanas básicas para la suma y cuatro para la multiplicación:

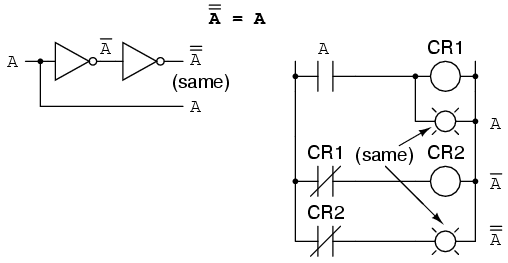
Otra identidad que tiene que ver con la complementación es la del doble complemento: una variable invertida dos veces. Complementar una variable dos veces (o cualquier número par de veces) da como resultado el valor booleano original. Esto es análogo a negar (multiplicar por -1) en álgebra de número real: un número par de negaciones se cancela para dejar el valor original:

Support Center

How can we help?