1.2: Formas de onda de CA
- Page ID
- 153396
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Cuando un alternador produce voltaje de CA, el voltaje cambia la polaridad con el tiempo, pero lo hace de una manera muy particular. Cuando se grafica a lo largo del tiempo, la “onda” trazada por este voltaje de polaridad alterna de un alternador adquiere una forma distinta, conocida como onda sinusoidal: Figura a continuación
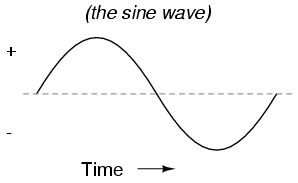
Gráfica de voltaje de CA a lo largo del tiempo (la onda sinusoidal).
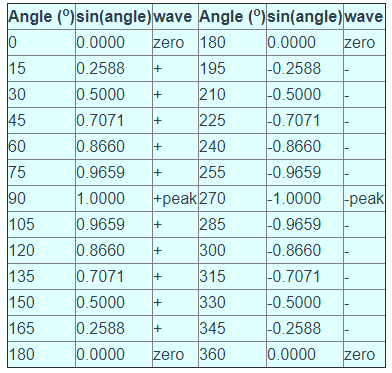
En la gráfica de voltaje de un alternador electromecánico, el cambio de una polaridad a otra es suave, cambiando el nivel de voltaje más rápidamente en el punto cero (“crossover”) y más lentamente en su pico. Si tuviéramos que graficar la función trigonométrica de “seno” en un rango horizontal de 0 a 360 grados, encontraríamos exactamente el mismo patrón que en la Tabla siguiente.
Función trigonométrica “sinusoidal”.
La razón por la que un alternador electromecánico emite CA de onda sinusoidal se debe a la física de su funcionamiento. El voltaje producido por las bobinas estacionarias por el movimiento del imán giratorio es proporcional a la velocidad a la que el flujo magnético está cambiando perpendicular a las bobinas (Ley de Inducción Electromagnética de Faraday). Esa tasa es mayor cuando los polos magnéticos están más cerca de las bobinas, y menos cuando los polos magnéticos están más alejados de las bobinas. Matemáticamente, la tasa de cambio de flujo magnético debido a un imán giratorio sigue la de una función sinusoidal, por lo que el voltaje producido por las bobinas sigue esa misma función.
Si tuviéramos que seguir el voltaje cambiante producido por una bobina en un alternador desde cualquier punto del gráfico de onda sinusoidal hasta ese punto cuando la forma de onda comienza a repetirse, habríamos marcado exactamente un ciclo de esa onda. Esto se muestra más fácilmente abarcando la distancia entre picos idénticos, pero puede medirse entre cualquier punto correspondiente en la gráfica. Las marcas de grado en el eje horizontal de la gráfica representan el dominio de la función sinusoidal trigonométrica, y también la posición angular de nuestro eje alternador simple de dos polos a medida que gira: Figura abajo
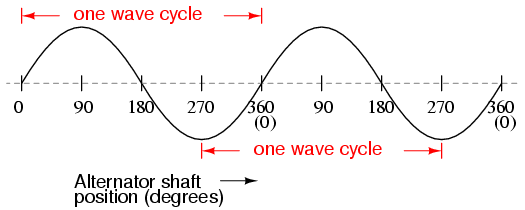
Voltaje del alternador en función de la posición del eje (tiempo).
Dado que el eje horizontal de esta gráfica puede marcar el paso del tiempo así como la posición del eje en grados, la dimensión marcada para un ciclo a menudo se mide en una unidad de tiempo, la mayoría de las veces segundos o fracciones de segundo. Cuando se expresa como una medida, esto a menudo se llama el período de una onda. El período de una onda en grados es siempre 360, pero la cantidad de tiempo que ocupa un período depende de la tasa de voltaje oscila de un lado a otro.
Una medida más popular para describir la tasa alterna de un voltaje de CA o una onda de corriente que el período es la tasa de esa oscilación de ida y vuelta. A esto se le llama frecuencia. La unidad moderna para frecuencia es el Hertz (abreviado Hz), que representa el número de ciclos de onda completados durante un segundo de tiempo. En los Estados Unidos de América, la frecuencia estándar de la línea eléctrica es de 60 Hz, lo que significa que el voltaje de CA oscila a una velocidad de 60 ciclos completos de ida y vuelta cada segundo. En Europa, donde la frecuencia del sistema de alimentación es de 50 Hz, el voltaje de CA solo completa 50 ciclos cada segundo. Un transmisor de estación de radio que emite a una frecuencia de 100 MHz genera un voltaje de CA que oscila a una velocidad de 100 millones de ciclos cada segundo.
Antes de la canonización de la unidad Hertz, la frecuencia se expresaba simplemente como “ciclos por segundo”. Los medidores más antiguos y los equipos electrónicos a menudo tenían unidades de frecuencia de “CPS” (Ciclos por segundo) en lugar de Hz. Mucha gente cree que el cambio de unidades autoexplicativas como CPS a Hertz constituye un paso atrás en claridad. Un cambio similar ocurrió cuando la unidad de “Celsius” reemplazó a la de “Centígrados” para la medición métrica de temperatura. El nombre Centígrado se basó en una escala de 100 conteos (“Centi-”) (“-grado”) que representa los puntos de fusión y ebullición de H 2 O, respectivamente. El nombre Celsius, en cambio, no da ninguna pista en cuanto al origen o significado de la unidad.
Periodo y frecuencia son recíprocos matemáticos entre sí. Es decir, si una onda tiene un periodo de 10 segundos, su frecuencia será de 0.1 Hz, o 1/10 de un ciclo por segundo:
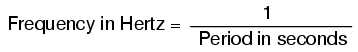
Un instrumento llamado osciloscopio, Figura a continuación, se utiliza para mostrar un voltaje cambiante a lo largo del tiempo en una pantalla gráfica. Puede estar familiarizado con la apariencia de una máquina de ECG o ECG (electrocardiógrafo), utilizada por los médicos para graficar las oscilaciones del corazón de un paciente a lo largo del tiempo. El ECG es un osciloscopio de propósito especial diseñado expresamente para uso médico. Los osciloscopios de propósito general tienen la capacidad de mostrar voltaje de prácticamente cualquier fuente de voltaje, trazados como un gráfico con el tiempo como variable independiente. La relación entre el período y la frecuencia es muy útil para conocer al momento de mostrar una forma de onda de voltaje o corriente de CA en una pantalla de osciloscopio. Al medir el periodo de la onda en el eje horizontal de la pantalla del osciloscopio y alternar ese valor de tiempo (en segundos), se puede determinar la frecuencia en Hertz.
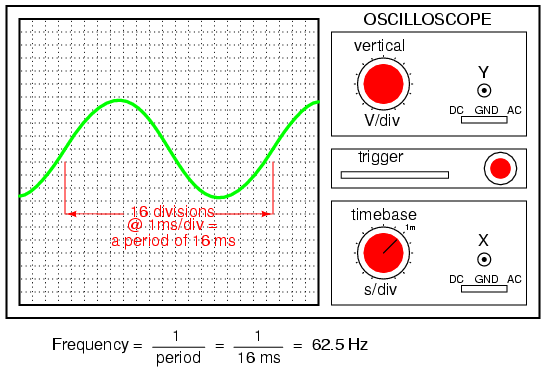
El voltaje y la corriente no son de ninguna manera las únicas variables físicas sujetas a variación a lo largo del tiempo. Mucho más común a nuestra experiencia cotidiana es el sonido, que no es más que la alternancia de compresión y descompresión (ondas de presión) de las moléculas de aire, interpretadas por nuestros oídos como una sensación física. Debido a que la corriente alterna es un fenómeno de onda, comparte muchas de las propiedades de otros fenómenos de onda, como el sonido. Por esta razón, el sonido (especialmente la música estructurada) proporciona una excelente analogía para relacionar conceptos de AC.
En términos musicales, la frecuencia es equivalente al tono. Las notas de tono bajo como las producidas por una tuba o fagot consisten en vibraciones de moléculas de aire que son relativamente lentas (baja frecuencia). Las notas de tono alto como las producidas por una flauta o silbato consisten en el mismo tipo de vibraciones en el aire, solo que vibran a una velocidad mucho más rápida (frecuencia más alta). La siguiente figura es una tabla que muestra las frecuencias reales para una gama de notas musicales comunes.

La frecuencia en Hertz (Hz) se muestra para diversas notas musicales.
Observadores astutos notarán que todas las notas sobre la mesa que llevan la misma designación de letra están relacionadas por una relación de frecuencia de 2:1. Por ejemplo, la primera frecuencia mostrada (designada con la letra “A”) es de 220 Hz. La siguiente nota “A” más alta tiene una frecuencia de 440 Hz, exactamente el doble de ciclos de ondas sonoras por segundo. La misma relación 2:1 se mantiene cierta para la primera A aguda (233.08 Hz) y la siguiente A aguda (466.16 Hz), y para todos los pares de notas que se encuentran en la tabla.
Audiblemente, dos notas cuyas frecuencias son exactamente el doble entre sí suenan notablemente similares. Esta similitud en el sonido es reconocida musicalmente, llamándose octava el lapso más corto en una escala musical que separa tales pares de notas. Siguiendo esta regla, la siguiente nota “A” más alta (una octava por encima de 440 Hz) será 880 Hz, la siguiente “A” más baja (una octava por debajo de 220 Hz) será de 110 Hz. Una vista de un teclado de piano ayuda a poner esta escala en perspectiva: Figura abajo
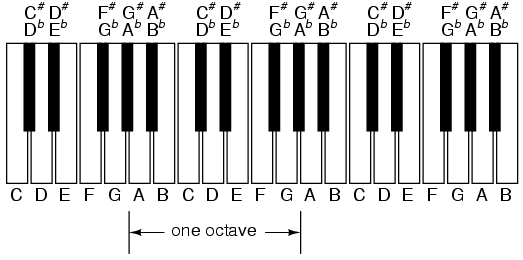
Una octava se muestra en un teclado musical.
Como puede ver, una octava equivale a siete teclas blancas de distancia en un teclado de piano. El familiar mnemotécnico musical (doe-ray-mee-fah-so-lah-tee) —sí, el mismo patrón inmortalizado en la caprichosa canción de Rodgers y Hammerstein cantada en
El sonido de la música: abarca una octava de C a C.
Si bien los alternadores electromecánicos y muchos otros fenómenos físicos producen naturalmente ondas sinusoidales, este no es el único tipo de onda alterna que existe. Otras “formas de onda” de CA se producen comúnmente dentro de los circuitos electrónicos. Aquí hay solo algunas formas de onda de muestra y sus designaciones comunes en la figura a continuación
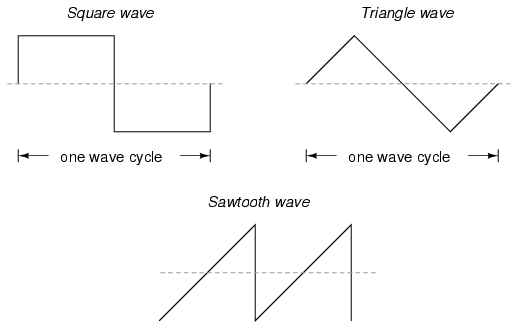
- REVISIÓN:
La CA producida por un alternador electromecánico sigue la forma gráfica de una onda sinusoidal.
Un ciclo de una ola es una evolución completa de su forma hasta el punto en que está lista para repetirse.
El periodo de una ola es la cantidad de tiempo que se tarda en completar un ciclo.
La frecuencia es el número de ciclos completos que una onda completa en una cantidad de tiempo determinada. Generalmente se mide en Hertz (Hz), siendo 1 Hz igual a un ciclo de onda completo por segundo.
Frecuencia = 1/ (periodo en segundos)


