11.3: Cálculo del factor de potencia
- Page ID
- 153445
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Como se mencionó anteriormente, el ángulo de este “triángulo de poder” indica gráficamente la relación entre la cantidad de potencia disipada (o consumida) y la cantidad de potencia absorbida/devuelta. También pasa a ser el mismo ángulo que el de la impedancia del circuito en forma polar. Cuando se expresa como una fracción, esta relación entre la potencia verdadera y la potencia aparente se denomina factor de potencia para este circuito. Debido a que la potencia verdadera y la potencia aparente forman los lados adyacente e hipotenusa de un triángulo rectángulo, respectivamente, la relación del factor de potencia también es igual al coseno de ese ángulo de fase. Usando valores del último circuito de ejemplo:

Cabe señalar que el factor de potencia, como todas las mediciones de relación, es una cantidad sin unidad.
Para el circuito puramente resistivo, el factor de potencia es 1 (perfecto), porque la potencia reactiva es igual a cero. Aquí, el triángulo de potencia se vería como una línea horizontal, porque el lado opuesto (potencia reactiva) tendría longitud cero.
Para el circuito puramente inductivo, el factor de potencia es cero, porque la potencia verdadera es igual a cero. Aquí, el triángulo de potencia se vería como una línea vertical, porque el lado adyacente (potencia verdadera) tendría longitud cero.
Lo mismo podría decirse de un circuito puramente capacitivo. Si no hay componentes disipativos (resistivos) en el circuito, entonces la verdadera potencia debe ser igual a cero, haciendo que cualquier potencia en el circuito sea puramente reactiva. El triángulo de potencia para un circuito puramente capacitivo volvería a ser una línea vertical (apuntando hacia abajo en lugar de hacia arriba como lo era para el circuito puramente inductivo).
El factor de potencia puede ser un aspecto importante a considerar en un circuito de CA debido a que cualquier factor de potencia menor a 1 significa que el cableado del circuito tiene que transportar más corriente de la que sería necesaria con una reactancia cero en el circuito para entregar la misma cantidad de energía (verdadera) a la carga resistiva. Si nuestro último ejemplo de circuito hubiera sido puramente resistivo, habríamos podido entregar 169.256 watts completos a la carga con los mismos 1.410 amperios de corriente, en lugar de los meros 119.365 vatios que actualmente está disipando con esa misma cantidad de corriente. El factor de potencia deficiente lo convierte en un sistema de suministro de energía ineficiente.
El factor de potencia deficiente puede corregirse, paradójicamente, agregando otra carga al circuito dibujando una cantidad igual y opuesta de potencia reactiva, para cancelar los efectos de la reactancia inductiva de la carga. La reactancia inductiva solo se puede cancelar por reactancia capacitiva, por lo que tenemos que agregar un condensador en paralelo a nuestro circuito de ejemplo como carga adicional. El efecto de estas dos reactancias opuestas en paralelo es llevar la impedancia total del circuito igual a su resistencia total (para hacer que el ángulo de fase de la impedancia sea igual, o al menos más cercano, a cero).
Como sabemos que la potencia reactiva (no corregida) es 119.998 VAR (inductiva), necesitamos calcular el tamaño correcto del condensador para producir la misma cantidad de potencia reactiva (capacitiva). Dado que este condensador estará directamente en paralelo con la fuente (de voltaje conocido), usaremos la fórmula de potencia que comienza a partir del voltaje y la reactancia:
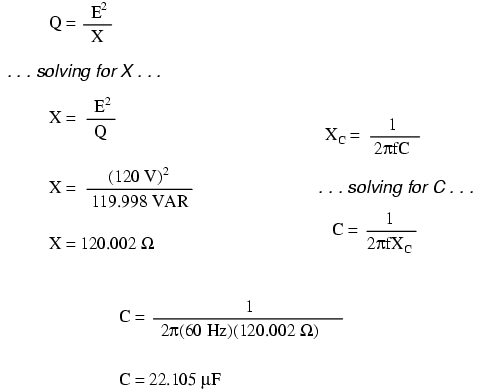
Usemos un valor de condensador redondeado de 22 µF y veamos qué sucede con nuestro circuito: (Figura a continuación)
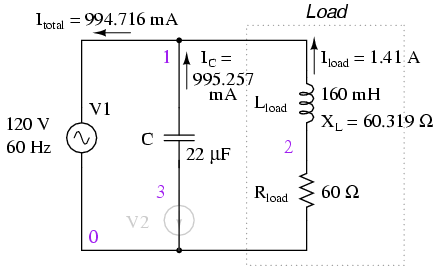
El condensador paralelo corrige el factor de potencia de retraso de la carga inductiva. V2 y los números de nodo: 0, 1, 2 y 3 están relacionados con SPICE y pueden ignorarse por el momento.

El factor de potencia para el circuito, en general, se ha mejorado sustancialmente. La corriente principal se ha reducido de 1.41 amperios a 994.7 miliamperios, mientras que la potencia disipada en la resistencia de carga permanece sin cambios en 119.365 vatios. El factor de potencia está mucho más cerca de ser 1:

Dado que el ángulo de impedancia sigue siendo un número positivo, sabemos que el circuito, en general, sigue siendo más inductivo que capacitivo. Si nuestros esfuerzos de corrección del factor de potencia hubieran estado perfectamente en el blanco, habríamos llegado a un ángulo de impedancia de exactamente cero, o puramente resistivo. Si hubiéramos agregado un condensador demasiado grande en paralelo, habríamos terminado con un ángulo de impedancia que era negativo, indicando que el circuito era más capacitivo que inductivo.
Una simulación SPICE del circuito de (Figura anterior) muestra que el voltaje total y la corriente total están casi en fase. El archivo de circuito SPICE tiene una fuente de voltaje de cero voltios (V2) en serie con el condensador para que se pueda medir la corriente del condensador. El tiempo de inicio de 200 ms (en lugar de 0) en la sentencia de análisis transitorio permite que las condiciones de CC se estabilicen antes de recopilar datos. Ver listado de SPICE “factor de potencia pf.cir”.
La gráfica de nuez moscada de las diversas corrientes con respecto a la tensión aplicada V total se muestra en (Figura a continuación). La referencia es V total, con lo que se comparan todas las demás mediciones. Esto se debe a que el voltaje aplicado, V total, aparece a través de las ramas paralelas del circuito. No hay corriente única común a todos los componentes. Podemos comparar esas corrientes con V total.
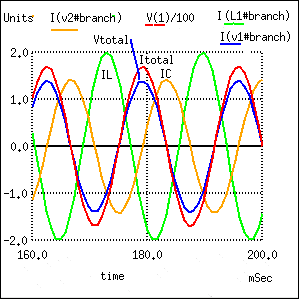
Ángulo de fase cero debido al total V en fase y I total. El rezagado I L con respecto al total de V se corrige con un I C líder.
Tenga en cuenta que la corriente total (I total) está en fase con la tensión aplicada (V total), lo que indica un ángulo de fase cercano a cero. Esto no es una coincidencia. Tenga en cuenta que la corriente rezagada, I L del inductor habría provocado que la corriente total tuviera una fase de retraso en algún lugar entre (I total) e I L. Sin embargo, la corriente principal del condensador, I C, compensa la corriente del inductor rezagado. El resultado es un ángulo de fase de corriente total en algún lugar entre las corrientes del inductor y el condensador. Además, esa corriente total (I total) se vio obligada a estar en fase con el voltaje total aplicado (V total), mediante el cálculo de un valor de condensador apropiado.
Dado que el voltaje y la corriente totales están en fase, el producto de estas dos formas de onda, la potencia, siempre será positivo a lo largo de un ciclo de 60 Hz, potencia real como en la Figura anterior. Si el ángulo de fase no hubiera sido corregido a cero (PF=1), el producto habría sido negativo donde porciones positivas de una forma de onda se superponían a partes negativas de la otra como en la Figura anterior. La energía negativa se retroalimenta al generador. No se puede vender; sin embargo, hace desperdicio de energía en la resistencia de las líneas eléctricas entre carga y generador. El condensador paralelo corrige este problema.
Tenga en cuenta que la reducción de las pérdidas de línea se aplica a las líneas desde el generador hasta el punto donde se aplica el condensador de corrección del factor de potencia. En otras palabras, todavía hay corriente circulante entre el condensador y la carga inductiva. Esto normalmente no es un problema porque la corrección del factor de potencia se aplica cerca de la carga infractora, como un motor de inducción.
Cabe señalar que demasiada capacitancia en un circuito de CA dará como resultado un factor de potencia bajo igual de bien como demasiada inductancia. Debe tener cuidado de no corregir en exceso al agregar capacitancia a un circuito de CA. También debe tener mucho cuidado al usar los condensadores adecuados para el trabajo (clasificados adecuadamente para los voltajes del sistema de energía y el pico de voltaje ocasional de los rayos, para el servicio continuo de CA y capaz de manejar los niveles esperados de corriente).
Si un circuito es predominantemente inductivo, decimos que su factor de potencia está rezagado (porque la onda de corriente para el circuito va por detrás de la onda de voltaje aplicada). Por el contrario, si un circuito es predominantemente capacitivo, decimos que su factor de potencia es líder. Así, nuestro circuito de ejemplo comenzó con un factor de potencia de 0.705 rezagado, y se corrigió a un factor de potencia de 0.999 rezagado.
Revisar
- El factor de potencia deficiente en un circuito de CA puede ser “corregido”, o restablecido a un valor cercano a 1, agregando una reactancia paralela opuesta al efecto de la reactancia de la carga. Si la reactancia de la carga es de naturaleza inductiva (que casi siempre lo será), la capacitancia paralela es lo que se necesita para corregir el factor de potencia deficiente.


