11.4: Corrección práctica del factor de potencia
- Page ID
- 153446
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Cuando surja la necesidad de corregir el factor de potencia deficiente en un sistema de alimentación de CA, probablemente no tendrá el lujo de conocer la inductancia exacta de la carga en henrys para usar en sus cálculos.
Puede que tengas la suerte de tener un instrumento llamado medidor de factor de potencia para decirte cuál es el factor de potencia (un número entre 0 y 1), y la potencia aparente (que se puede calcular tomando un voltímetro leyendo en voltios y multiplicando por una lectura de amperímetro en amperios). En circunstancias menos favorables, es posible que tenga que usar un osciloscopio para comparar formas de onda de voltaje y corriente, medir el desplazamiento de fase en grados y calcular el factor de potencia por el coseno de ese desplazamiento de fase.
Lo más probable es que tenga acceso a un vatímetro para medir la potencia verdadera, cuya lectura puede comparar con un cálculo de potencia aparente (a partir de multiplicar las mediciones de voltaje total y corriente total). A partir de los valores de potencia verdadera y aparente, puede determinar la potencia reactiva y el factor de potencia.
Hagamos un problema de ejemplo para ver cómo funciona esto: (Figura abajo)
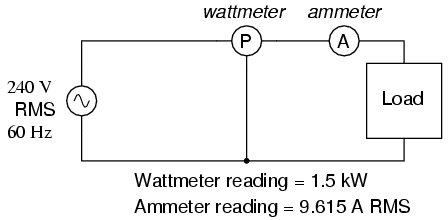
El vatímetro lee la potencia real; producto de las lecturas de voltímetro y amperímetro produce potencia aparente.
Cómo calcular la potencia aparente en kVA
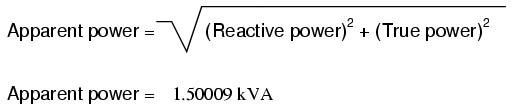
Primero, necesitamos calcular la potencia aparente en kVA. Podemos hacer esto multiplicando el voltaje de carga por la corriente de carga:

Como podemos ver, 2.308 kVA es una cifra mucho mayor que 1.5 kW, lo que nos dice que el factor de potencia en este circuito es bastante pobre (sustancialmente menor que 1). Ahora, calculamos el factor de potencia de esta carga dividiendo el verdadero poder por el poder aparente:

Usando este valor para el factor de potencia, podemos dibujar un triángulo de potencia, y a partir de eso determinar la potencia reactiva de esta carga: (Figura a continuación)
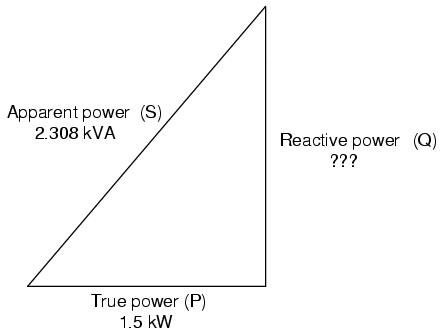
La potencia reactiva puede calcularse a partir de la potencia verdadera y la potencia aparente.
Cómo Usar el Teorema de Pitágoras para Determinar la Cantidad Desconocida del Triángulo
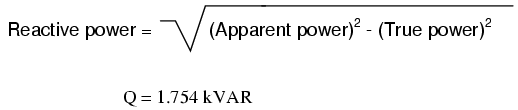
Para determinar la cantidad desconocida del triángulo (poder reactivo), usamos el Teorema de Pitágoras “al revés”, dada la longitud de la hipotenusa (poder aparente) y la longitud del lado adyacente (poder verdadero):
Cómo corregir el factor de potencia con un condensador
Si esta carga es un motor eléctrico o casi cualquier otra carga de CA industrial, tendrá un factor de potencia rezagado (inductivo), lo que significa que tendremos que corregirlo con un condensador de tamaño apropiado, cableado en paralelo. Ahora que conocemos la cantidad de potencia reactiva (1.754 kVar), podemos calcular el tamaño del condensador necesario para contrarrestar sus efectos:

Redondeando esta respuesta a 80 µF, podemos colocar ese tamaño de condensador en el circuito y calcular los resultados: (Figura a continuación)
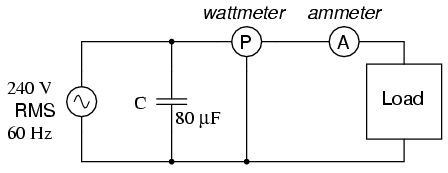
El condensador paralelo corrige la carga de retraso (inductivo).
Un condensador de 80 µF tendrá una reactancia capacitiva de 33.157 Ω, dando una corriente de 7.238 amperios, y una potencia reactiva correspondiente de 1.737 kVar (solo para el condensador). Dado que la corriente del condensador es 180 o desfasada de la contribución inductiva de la carga al consumo de corriente, la potencia reactiva del condensador restará directamente de la potencia reactiva de la carga, resultando en:
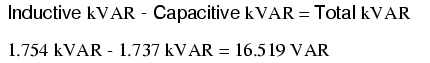
Esta corrección, por supuesto, no cambiará la cantidad de energía verdadera consumida por la carga, sino que dará como resultado una reducción sustancial de la potencia aparente, y de la corriente total extraída de la fuente de 240 voltios: (Figura a continuación)
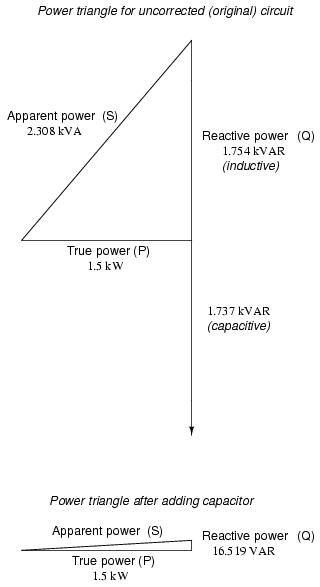
Triángulo de potencia antes y después de la corrección del condensador.
El nuevo poder aparente se puede encontrar a partir de los valores de potencia reactiva verdadero y nuevo, utilizando la forma estándar del Teorema de Pitágoras: