2.1: Gráficas de las funciones coseno y seno
- Page ID
- 113302
Preguntas de enfoque
Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.
- ¿Cuáles son las gráficas y las propiedades importantes de las gráficas de\(y = \cos(x)\) y\(y = \sin(x)\)?
- ¿Cuáles son los dominios de las funciones seno y coseno? ¿Cuáles son los rangos de las funciones seno y coseno?
- ¿Cuáles son los periodos de las funciones seno y coseno? ¿Qué significa period?
- ¿Qué es la amplitud? ¿Cómo afecta la amplitud a la gráfica del seno o coseno?
Actividad de inicio
La forma más básica de dibujar la gráfica de una función es trazar puntos. Utilice los valores en la tabla dada para trazar los puntos en la gráfica de\(y = \sin(x)\) y luego dibujar la gráfica de\(y = \sin(t)\) for\(0 < t < 2\pi\). Nota: En el\(t\) eje -las líneas de cuadrícula están separadas por\(\dfrac{\pi}{12}\) unidades y en el\(y\) eje -las líneas de cuadrícula están separadas por 0.1 de una unidad.

| \(t\) | \(\sin(t)\) | \(\sin(t)\)(aprox.) |
|---|---|---|
| \ (t\)” style="vertical-align: middle; ">0 | \ (\ sin (t)\)” style="vertical-align: middle; ">0 | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">0 |
| \ (t\)” style="vertical-align: middle; ">\(\dfrac{\pi}{6}\) | \ (\ sin (t)\)” style="vertical-align: middle; ">\(\dfrac{1}{2}\) | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">0.5 |
| \ (t\)” style="vertical-align: middle; ">\(\dfrac{\pi}{4}\) | \ (\ sin (t)\)” style="vertical-align: middle; ">\(\dfrac{\sqrt{2}}{2}\) | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">0.707 |
| \ (t\)” style="vertical-align: middle; ">\(\dfrac{\pi}{3}\) | \ (\ sin (t)\)” style="vertical-align: middle; ">\(\dfrac{\sqrt{3}}{2}\) | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">0.866 |
| \ (t\)” style="vertical-align: middle; ">\(\dfrac{\pi}{2}\) | \ (\ sin (t)\)” style="vertical-align: middle; ">1 | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">1 |
| \ (t\)” style="vertical-align: middle; ">\(\dfrac{2\pi}{3}\) | \ (\ sin (t)\)” style="vertical-align: middle; ">\(\dfrac{\sqrt{3}}{2}\) | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">0.866 |
| \ (t\)” style="vertical-align: middle; ">\(\dfrac{3\pi}{4}\) | \ (\ sin (t)\)” style="vertical-align: middle; ">\(\dfrac{\sqrt{2}}{2}\) | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">0.714 |
| \ (t\)” style="vertical-align: middle; ">\(\dfrac{5\pi}{6}\) | \ (\ sin (t)\)” style="vertical-align: middle; ">\(\dfrac{1}{2}\) | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">0.5 |
| \ (t\)” style="vertical-align: middle; ">\(\pi\) | \ (\ sin (t)\)” style="vertical-align: middle; ">0 | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">0 |
| \ (t\)” style="vertical-align: middle; ">\(\dfrac{7\pi}{6}\) | \ (\ sin (t)\)” style="vertical-align: middle; ">\(-\dfrac{1}{2}\) | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">-0.5 |
| \ (t\)” style="vertical-align: middle; ">\(\dfrac{5\pi}{4}\) | \ (\ sin (t)\)” style="vertical-align: middle; ">\(-\dfrac{\sqrt{2}}{2}\) | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">-0.707 |
| \ (t\)” style="vertical-align: middle; ">\(\dfrac{4\pi}{3}\) | \ (\ sin (t)\)” style="vertical-align: middle; ">\(-\dfrac{\sqrt{3}}{2}\) | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">-0.866 |
| \ (t\)” style="vertical-align: middle; ">\(\dfrac{3\pi}{2}\) | \ (\ sin (t)\)” style="vertical-align: middle; ">-1 | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">-1 |
| \ (t\)” style="vertical-align: middle; ">\(\dfrac{5\pi}{3}\) | \ (\ sin (t)\)” style="vertical-align: middle; ">\(-\dfrac{\sqrt{3}}{2}\) | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">-0.866 |
| \ (t\)” style="vertical-align: middle; ">\(\dfrac{7\pi}{4}\) | \ (\ sin (t)\)” style="vertical-align: middle; ">\(-\dfrac{\sqrt{2}}{2}\) | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">-0.707 |
| \ (t\)” style="vertical-align: middle; ">\(\dfrac{11\pi}{6}\) | \ (\ sin (t)\)” style="vertical-align: middle; ">\(-\dfrac{1}{2}\) | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">-0.5 |
| \ (t\)” style="vertical-align: middle; ">\(2\pi\) | \ (\ sin (t)\)” style="vertical-align: middle; ">0 | \ (\ sin (t)\) (aprox)” style="vertical-align: middle; ">0 |
También podemos usar una calculadora gráfica u otro dispositivo gráfico para dibujar la gráfica de la función sinusoidal. Asegúrese de que el dispositivo esté configurado en modo radián y úselo para dibujar el gráfico de\(y = \sin(t)\) uso\(-2\pi \leq t \leq 4\pi\) y\(-1.2 \leq t \leq 1.2\). Nota: Muchas utilidades gráficas requieren el uso de\(x\) como variable independiente. Para este tipo de dispositivos, necesitamos usar\(y = \sin(x)\). Esto no hará diferencia en la gráfica de la función.
- Compárelo con la gráfica de la parte (1). ¿Cuáles son las similitudes? ¿Cuáles son las diferencias?
- Encuentra cuatro valores separados de\(t\) donde la gráfica de la función sinusoidal cruza el\(t\) eje -axis. Tales valores se llaman\(t\) - intercepciones de la función sinusoidal (o raíces o ceros).
- A partir de las gráficas, lo que parece ser el valor máximo de\(\sin(t)\). Determinar dos valores diferentes de los\(t\) que dan este valor máximo de\(\sin(t)\).
- A partir de las gráficas, lo que parece ser el valor mínimo de\(\sin(t)\). Determinar dos valores diferentes de los\(t\) que dan este valor mínimo de\(\sin(t)\).
Los periodos de las funciones sinusoidales y cosenales
Una cosa que podemos observar a partir de las gráficas de la función sinusoidal en la actividad inicial es que la gráfica parece tener forma de “onda” y que esta “onda” se repite a medida que nos movemos por el eje horizontal. Vemos que la porción de la gráfica entre 0 y\(2\pi\) parece idéntica a la porción de la gráfica entre\(2\pi\) y\(4\pi\) y a la porción de la gráfica entre\(-2\pi\) y 0. La gráfica de la función sinusoidal está exhibiendo lo que se conoce como una propiedad periódica. La Figura 2.1 muestra la gráfica de\(y = \sin(t)\) para tres ciclos.
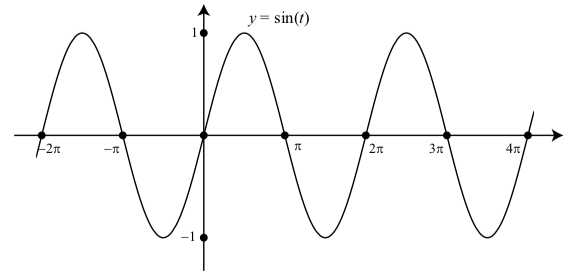
Figura\(\PageIndex{1}\): Gráfica de\(y = \sin(t)\) con\(-2\pi \leq t \leq 4\pi\)
Decimos que la función seno es una función periódica. Tales funciones se utilizan a menudo para modelar fenómenos repetitivos como un péndulo que se balancea hacia adelante y hacia atrás, un peso unido a un resorte y una cuerda de guitarra vibrante.
La razón por la que la gráfica de\(y = \sin(t)\) repeticiones es que el valor de\(\sin(t)\) es la coordenada y de un punto a medida que se mueve alrededor del círculo unitario. Dado que la circunferencia del círculo unitario es\(2\pi\) unidades, un arco de longitud\((t + 2\pi)\) tendrá el mismo punto terminal que un arco de longitud t, ya que\(\sin(t)\) es la coordenada y de este punto, vemos eso\(\sin(t + 2\pi) = \sin(t)\). Esto quiere decir que el periodo de la función sinusoidal es\(2\pi\). A continuación se presenta una definición más formal de una función periódica.
Definición
Definición. Una función\(f\) es periódica con punto\(p\) si\(f(t + p) = f(t)\) para todos\(t\) en el dominio de\(f\) y\(p\) es el número positivo más pequeño que tiene esta propiedad.
Observe que si\(f\) es una función periódica con punto\(p\), entonces si agregamos 2\(p\) a\(t\), obtenemos\[f(t + 2p) = f((t+p)+p) = f(t + p) =f(t).\]
Podemos seguir repitiendo este proceso y ver que para cualquier entero\(k\),\[f(t + kp) =f(t).\]
Hasta ahora, hemos estado discutiendo solo la función sinusoidal, pero obtenemos un comportamiento similar con la función coseno. Recuerde que la función de envoltura envuelve la línea numérica alrededor del círculo unitario de una manera que se repite en segmentos de longitud\(2\pi\). Este es un comportamiento periódico y conduce a un comportamiento periódico tanto de las funciones seno como coseno ya que el valor de la función sinusoidal es la\(y\) coordenada -de un punto en el círculo unitario y el valor de la función coseno es la\(x\) coordenada -del mismo punto en el círculo unitario, el seno y las funciones coseno se repiten cada vez que hacemos una envoltura alrededor del círculo unitario. Es decir,\[\cos(t + 2\pi) = \cos(t) \space and \space \sin(t + 2\pi) = \sin(t).\]
es importante reconocer que\(2\pi\) es el número más pequeño que hace que esto suceda. Por lo tanto, las funciones coseno y seno son periódicas con periodo\(2\pi\).
Ejercicio\(\PageIndex{1}\)
Podemos, por supuesto, utilizar una utilidad gráfica para dibujar la gráfica de la función coseno. Sin embargo, sí ayuda a entender la gráfica si realmente dibujamos la gráfica a mano como hicimos para la función sinusoidal en la actividad inicial. Utilice los valores en la tabla dada para trazar los puntos en la gráfica de\(y = \cos(t)\) y luego dibujar la gráfica de\(y = \cos(t)\) for\(0 \leq t \leq 2\pi\).

| \(t\) | \(\cos(t)\) | \(\cos(t)\)(aprox.) |
|---|---|---|
| \ (t\) ">\(0\) | \ (\ cos (t)\) ">\(1\) | \ (\ cos (t)\) (aprox) ">\(1\) |
| \ (t\) ">\(\dfrac{\pi}{6}\) | \ (\ cos (t)\) ">\(\dfrac{\sqrt{3}}{2}\) | \ (\ cos (t)\) (aprox) ">\(0.866\) |
| \ (t\) ">\(\dfrac{\pi}{4}\) | \ (\ cos (t)\) ">\(\dfrac{\sqrt{2}}{2}\) | \ (\ cos (t)\) (aprox) ">\(0.707\) |
| \ (t\) ">\(\dfrac{\pi}{3}\) | \ (\ cos (t)\) ">\(\dfrac{1}{2}\) | \ (\ cos (t)\) (aprox) ">\(0.5\) |
| \ (t\) ">\(\dfrac{\pi}{2}\) | \ (\ cos (t)\) ">\(0\) | \ (\ cos (t)\) (aprox) ">\(0\) |
| \ (t\) ">\(\dfrac{2\pi}{3}\) | \ (\ cos (t)\) ">\(-\dfrac{1}{2}\) | \ (\ cos (t)\) (aprox) ">\(-0.5\) |
| \ (t\) ">\(\dfrac{3\pi}{4}\) | \ (\ cos (t)\) ">\(-\dfrac{\sqrt{2}}{2}\) | \ (\ cos (t)\) (aprox) ">\(-0.714\) |
| \ (t\) ">\(\dfrac{5\pi}{6}\) | \ (\ cos (t)\) ">\(-\dfrac{\sqrt{3}}{2}\) | \ (\ cos (t)\) (aprox) ">\(-0.866\) |
| \ (t\) ">\(\pi\) | \ (\ cos (t)\) ">\(-1\) | \ (\ cos (t)\) (aprox) ">\(-1\) |
| \ (t\) ">\(\dfrac{7\pi}{6}\) | \ (\ cos (t)\) ">\(-\dfrac{\sqrt{3}}{2}\) | \ (\ cos (t)\) (aprox) ">\(-0.866\) |
| \ (t\) ">\(\dfrac{5\pi}{4}\) | \ (\ cos (t)\) ">\(-\dfrac{\sqrt{2}}{2}\) | \ (\ cos (t)\) (aprox) ">\(-0.714\) |
| \ (t\) ">\(\dfrac{4\pi}{3}\) | \ (\ cos (t)\) ">\(-\dfrac{1}{2}\) | \ (\ cos (t)\) (aprox) ">\(-0.5\) |
| \ (t\) ">\(\dfrac{3\pi}{2}\) | \ (\ cos (t)\) ">\(0\) | \ (\ cos (t)\) (aprox) ">\(-1\) |
| \ (t\) ">\(\dfrac{5\pi}{3}\) | \ (\ cos (t)\) ">\(\dfrac{1}{2}\) | \ (\ cos (t)\) (aprox) ">\(0.5\) |
| \ (t\) ">\(\dfrac{7\pi}{4}\) | \ (\ cos (t)\) ">\(-\dfrac{\sqrt{2}}{2}\) | \ (\ cos (t)\) (aprox) ">\(0.707\) |
| \ (t\) ">\(\dfrac{11\pi}{6}\) | \ (\ cos (t)\) ">\(\dfrac{\sqrt{3}}{2}\) | \ (\ cos (t)\) (aprox) ">\(-0.866\) |
| \ (t\) ">\(2\pi\) | \ (\ cos (t)\) ">\(1\) | \ (\ cos (t)\) (aprox) ">\(1\) |
- Contestar
-
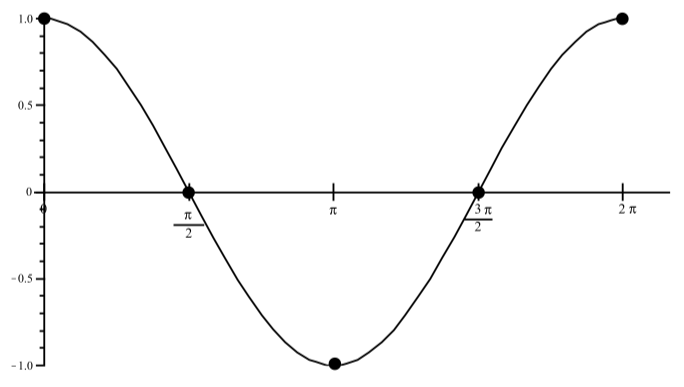
No se trazan todos los puntos, pero la siguiente es una gráfica de un periodo completo de\(y = \cos(t)\) para\(0 \leq t \leq 2\pi\).
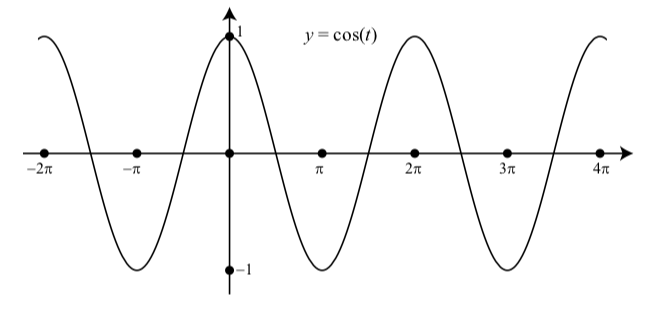
Figura\(\PageIndex{2}\): Gráfica de\(y = \cos(t)\) con\(-2\pi \leq t \leq 4\pi\)
Ejercicio\(\PageIndex{2}\)
- Compara la gráfica en Figura\(\PageIndex{2}\) con la gráfica de Ejercicio\(\PageIndex{1}\). ¿Cuáles son las similitudes? ¿Cuáles son las diferencias?
- Encuentra cuatro valores separados de\(t\) donde la gráfica de la función coseno cruza el\(t\) eje -eje. Tales valores se llaman\(t\) - intercepciones de la función coseno (o raíces o ceros).
- A partir de las gráficas, lo que parece ser el valor máximo de\(\cos(t)\). Determinar dos valores diferentes de los\(t\) que dan este valor máximo de\(\cos(t)\).
- A partir de las gráficas, lo que parece ser el valor mínimo de\(\cos(t)\). Determinar dos valores diferentes de los\(t\) que dan este valor mínimo de\(\cos(t)\).
- Contestar
-
- La diferencia es que la gráfica de la Figura\(\PageIndex{2}\) muestra tres periodos completos de\(y = \cos(t)\) sobre el intervalo\([-2\pi, 4\pi]\).
- La gráfica de\(y = \cos(t)\) tiene\(t\) -intercepta en\(t = -\dfrac{3\pi}{2}, t = -\dfrac{\pi}{2}, t = \dfrac{\pi}{2}, t = \dfrac{3\pi}{2}, t = \dfrac{5\pi}{2}\), y\(t = \dfrac{7\pi}{2}\)
- El valor máximo de\(y = \cos(t)\) es\(1\). La gráfica alcanza este máximo en\(t = -2\pi, t = 0, t = 2\pi\), y\(t = 4\pi\).
- El valor mínimo de\(y = \cos(t)\) es\(-1\). La gráfica alcanza este mínimo en\(t = -\pi, t = \pi\), y\(t = 3\pi\)
Actividad 2.3 (Las gráficas de las funciones seno y coseno).
Ahora hemos construido la gráfica de las funciones seno y coseno trazando puntos y utilizando una utilidad gráfica. Podemos tener una mejor comprensión de estas gráficas si podemos ver cómo se relacionan estas gráficas con las definiciones de círculo unitario de\(\sin(t)\) y\(\cos(t)\). Utilizaremos dos applets de Geogebra para ayudarnos a hacer esto.
El primer applet se llama Sine Graph Generator. La dirección web es Gvsu.edu/s/ly
Para comenzar, basta con mover el control deslizante para\(t\) hasta obtener\(t = 1\) y observar la imagen resultante. A la izquierda, habrá una copia del círculo unitario con un arco dibujado que tiene longitud\(1\). También se mostrará la\(y\) coordenada -del punto terminal de este arco (\(0.84\)redondeado a la centésima más cercana). La línea horizontal se conectará al punto\((1, 0.84)\) en la gráfica de\(y = \sin(t)\). A medida que los valores de\(t\) se cambian con el deslizador, se dibujarán más puntos de esta manera en la gráfica de\(y = \sin(t)\).
El otro applet se llama Cosine Graph Generator y funciona de manera similar a Sine Graph Generator. La dirección web de este applet es http://gvsu.edu/s/Lz
Propiedades de las Gráficas de las Funciones Seno y Cosino
Las gráficas de\(y = \sin(t)\) y\(y = \cos(t)\) se denominan ondas sinusoidales y las funciones seno y coseno se denominan funciones sinusoidales. Ambas ondas sinusoidales particulares tienen un período de\(2\pi\). La gráfica a lo largo de un periodo se denomina ciclo de la gráfica. Al igual que con otras funciones en nuestro estudio previo del álgebra, otra propiedad importante de las gráficas son sus intercepciones, en particular, las intercepciones horizontales o los puntos donde la gráfica cruza el eje horizontal. Una gran diferencia con el álgebra es que las funciones seno y coseno tienen infinitamente muchas intercepciones horizontales.
En Ejercicio\(\PageIndex{2}\), utilizamos Figura\(\PageIndex{2}\) y determinamos que\(-\dfrac{\pi}{2}, \dfrac{\pi}{2}, \dfrac{3\pi}{2}, \dfrac{5\pi}{2}, \dfrac{7\pi}{2}\) son\(t\) -intercepciones en la gráfica de\(y = \cos(t)\). En particular, en el intervalo\([0, 2\pi]\), las únicas\(t\) -intercepciones de\(y = \cos(t)\) son\(t = \dfrac{\pi}{2}\) y\(t = \dfrac{3\pi}{2}\).
Hay, por supuesto, otros\(t\) -interceptos, y aquí es donde el periodo de\(2\pi\) es útil. Podemos generar cualquier otra\(t\) -intercepción de\(y = \cos(t)\) agregando múltiplos enteros del período\(2\pi\) a estos dos valores. Por ejemplo, si sumamos\(6\pi\) a cada uno de ellos, vemos eso\(t = \dfrac{13\pi}{2}\) y\(t = \dfrac{15\pi}{2}\) son\(t\) intercepciones de\(y = \cos(t)\).
Ejercicio\(\PageIndex{3}\)
Utilice una gráfica para determinar las\(t\) -intercepciones de\(y = \sin(t)\) en el intervalo\([0, 2\pi]\). Luego use la propiedad period de la función sinusoidal para determinar las\(t\) -intercepciones de\(y = \sin(t)\) en el intervalo\([-2\pi, 4\pi]\). Compare este resultado con la gráfica de la Figura 2.1. Finalmente, determinar dos\(t\) -intercepciones de\(y = \sin(t)\) que no están en el intervalo\([-2\pi, 4\pi]\).
- Contestar
-
La gráfica de\(y = \sin(t)\) tiene\(t\) -intercepciones de\(t = 0, t = \pi\), y\(t = 2\pi\) en el intervalo\([0, 2\pi]\).
Si sumamos el periodo de\(2\pi\) a cada una de estas\(t\) -intercepciones y restamos el periodo\(2\pi\) de de cada una de estas\(t\) -intercepciones, vemos que la gráfica de\(y = \sin(t)\) tiene\(t\) -intercepciones de\(t = -2\pi, t = -\pi, t = 0, t = \pi, t = 2\pi, t = 3\pi\), y\(t = 4\pi\) en el intervalo\([-2\pi, 4\pi]\).Podemos determinar otras\(t\) -intercepciones de sumando o\(y = \sin(t)\) restando repetidamente el período de\(2\pi\). Por ejemplo, hay una\(t\) -intercepción en:
- \(t = 3\pi + 2\pi = 5\pi\)
- \(t = 5\pi + 2\pi = 7\pi\)
No obstante, si miramos con más atención la gráfica de\(y = \sin(t)\), vemos que las\(t\) -intercepciones son\(\pi\) unidades espaciadas entre sí. Esto quiere decir que podemos decir que\(t = 0 + k\pi\), donde\(k\) hay algún entero, es una\(t\) -intercepción de\(y = \sin(t)\).
Actividad 2.5 (Exploración de gráficos de funciones sinusoidales)
Haga una de las siguientes acciones:
- Dibuja las gráficas de\(y = \sin(t)\),\(y = \dfrac{1}{2}\sin(t)\) y\(y = 2\sin(t)\),\(y = -\sin(t)\), y\(y = 2\sin(t)\) sobre los mismos ejes. Asegúrese de que su utilidad gráfica esté en modo radián y use\(-2\pi \leq x \leq 2\pi\) y\(-2.5 \leq x \leq 2.5\).
- Utilice el applet de Geogebra Amplitud de una Sinusoide en la siguiente dirección web: http://gvsu.edu/s/LM
La expresión for se\(g(t)\) puede cambiar pero dejarla establecida en\(g(t) = \sin(t)\). El deslizador se puede mover para cambiar el valor de A y se\(y = A\sin(t)\) dibujará la gráfica de. Explore estas gráficas cambiando los valores de A asegurándose de usar valores negativos de A así como valores positivos de A. (Es posible cambiar esto\(g(t) = \cos(t)\) y explorar las gráficas de\(y = A\sin(t)\).
La amplitud de las funciones sinusoidales y cosenales
Las gráficas de las funciones de la Actividad 2.5 deberían haber parecido a una de las gráficas de la Figura 2.3. Ambas gráficas son gráficas de\(y = A\sin(t)\), pero la de la izquierda es para\(A > 0\) y la de la derecha es para\(A < 0\). Tenga en cuenta que cuando\(A < 0\),\(-A > 0\). Otra característica importante de una onda sinusoidal es la amplitud. La amplitud de cada una de las gráficas de la Figura 2.3 está representada por la longitud de las líneas discontinuas, y vemos que esta longitud es igual a\(|A|\).
Definición: amplitud
La amplitud de una onda sinusoidal es la mitad de la distancia entre los valores funcionales máximo y mínimo.
\[\text{Amplitude} = \dfrac{1}{2}|(\text{ max y-coordinate}) - (\text{min y-coordinate})|\]
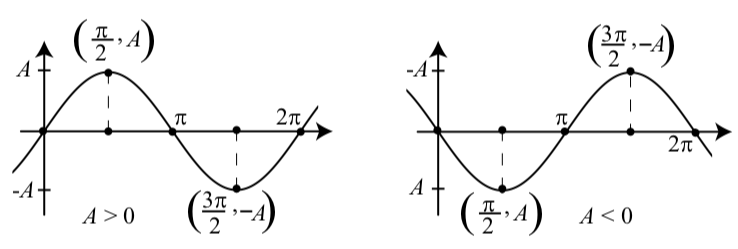
Figura\(\PageIndex{3}\): Gráficas de\(y = A\sin(t)\)
Ejercicio\(\PageIndex{4}\)
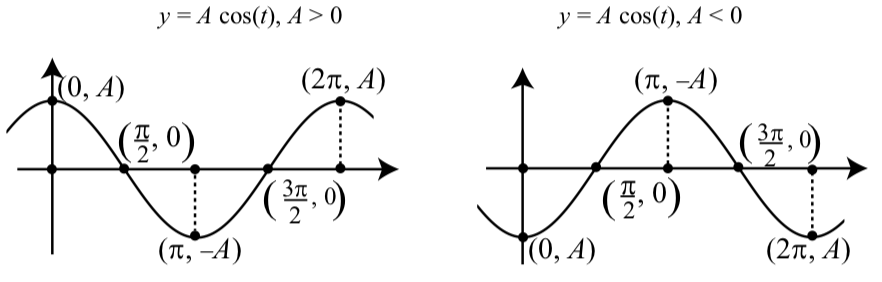
Dibujar gráficas de\(y = A\cos(t)\) para\(A > 0\) y para\(A < 0\) similares a las gráficas para\(y = A\sin(t)\) en la Figura\(\PageIndex{3}\).
- Contestar
-
Uso de una Utilidad Gráfica
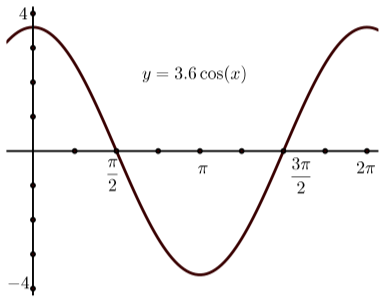
A menudo utilizaremos una utilidad gráfica para dibujar la gráfica de una función sinusoidal. Al hacerlo, es una buena idea usar la amplitud para ayudar a establecer una ventana de visualización adecuada. La idea básica es que la pantalla de la utilidad gráfica muestre algo más de un periodo de la sinusoide. Por ejemplo, si estamos tratando de dibujar una gráfica de\(y = 3.6\cos(t)\), podríamos usar la siguiente ventana de visualización. \[-0.5 \leq x \leq 6.5 \space and \space -4 \leq y \leq 4.\]Si es posible, establezca las marcas\(x\) -tickmarks para que sean todas\(\dfrac{\pi}{4}\) o\(\dfrac{\pi}{2}\) unidades.
Ejercicio\(\PageIndex{5}\)
- Utilice una utilidad gráfica para dibujar la gráfica de\(y = 3.6\cos(t)\) usar la ventana de visualización indicada antes de esta prueba de progreso.
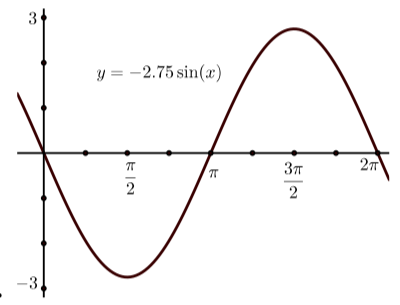
- Utilice una utilidad gráfica para dibujar la gráfica de\(y = -2.75\sin(t)\).
- Contestar
-
1.
2.
La simetría y las identidades negativas
Examine la gráfica de la que\(y = \cos(t)\) se muestra en la Figura 2.2. Si nos enfocamos en esa porción de la gráfica entre\(-2\pi\) y\(2\pi\), podemos notar que el lado izquierdo de la gráfica es la “imagen especular” del lado derecho de la gráfica. Para ver esto mejor, usa el applet Geogebra Simetría de la Gráfica de\(y = \cos(t)\) en el siguiente enlace: http://gvsu.edu/s/Ot
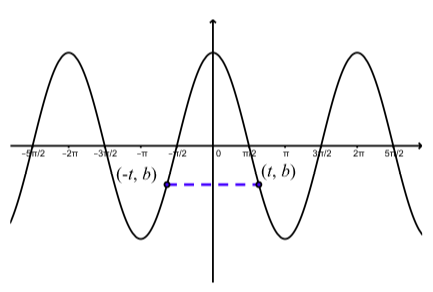
Figura\(\PageIndex{4}\): Gráfica que muestra la simetría de\(y = \cos(t)\)
La figura\(\PageIndex{4}\) muestra una imagen típica de este applet. Dado que la segunda coordenada de un punto en la gráfica es el valor de la función en la primera coordenada, esta figura (y applet) están indicando que\(b = \cos(t)\) y\(b = \cos(-t)\). Es decir, esto está ilustrando el hecho de que\(\cos(-t) = \cos(t)\). La siguiente actividad proporciona una explicación de por qué esto es cierto.
Actividad 2.8: Arcos positivos y Negativos
Para esta actividad, utilizaremos el applet de Geogebra llamado Dibujar un Arco Positivo y un Arco Negativo en el Círculo Unitario. Un enlace a este applet es http://gvsu.edu/s/Ol
A medida que se usa el deslizador para\(t\) en el applet, se dibujará un arco de longitud t en azul y se\(-t\) dibujará un arco de longitud en rojo. Además, se mostrarán las coordenadas de los puntos terminales tanto de los arcos\(t\) como de\(-t\) los arcos. Estudiar las coordenadas de estos dos puntos para diversos valores de\(t\). ¿Qué observas? Teniendo en cuenta que las coordenadas de estos puntos también se pueden representar como\[(\cos(t), \sin(t))\space and \space (\cos(-t), \sin(-t)),\]
¿Qué parecen indicar estos sobre la relación entre\(\cos(-t)\) y\(\cos(t)\)? ¿Y la relación entre\(\sin(-t)\) y\(\sin(t)\)?
La figura\(\PageIndex{5}\) muestra una situación típica ilustrada en la Actividad 2.8. Un arco y su correspondiente arco negativo han sido dibujados en el círculo unitario. Lo que hemos visto
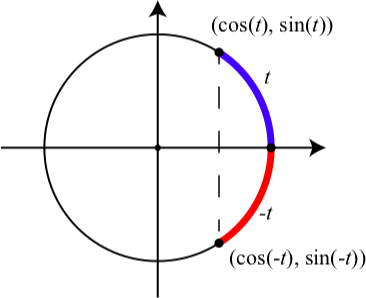
Figura\(\PageIndex{5}\): Un arco y un arco negativo en el círculo unitario
es que si el punto terminal del arco\(t\) es\((a, b)\), entonces por la simetría del círculo, vemos que el punto terminal del arco\(-t\) es\((a, -b)\). Entonces el diagrama ilustra los siguientes resultados, que a veces se denominan identidades de arco negativo.
Definición: Identidades de arco negativo
Por cada número real\(t\),\[\sin(-t) = -\sin(t) \space \cos(-t) = \cos(t).\]
Para verificar aún más las identidades de arco negativo para seno y coseno, use una utilidad gráfica para:
- Dibuja la gráfica de\(y = \cos(-x)\) usar\(0 \leq x \leq 2\pi\). La gráfica debe ser idéntica a la gráfica de\(y = \cos(x)\).
- Dibuja la gráfica de\(y = \sin(-x)\) usar\(0 \leq x \leq 2\pi\). La gráfica debe ser idéntica a la gráfica de\(y = \sin(x)\).
Estas llamadas identidades de arco negativo nos dan una manera de observar la simetría de las gráficas de las funciones coseno y seno. Ya hemos ilustrado la simetría de la función coseno en la Figura\(\PageIndex{4}\). Debido a esto, decimos que la gráfica de\(y = \cos(t)\) es simétrica alrededor del eje y.
¿Qué pasa con la simetría en la gráfica de la función sinusoidal? La figura\(\PageIndex{6}\) ilustra lo que\(\sin(-t) = \sin(t)\) implica la identidad negativa sobre la simetría de\(y = \sin(t)\). En este caso, decimos que la gráfica de\(y = \sin(t)\) es simétrica sobre el origen.
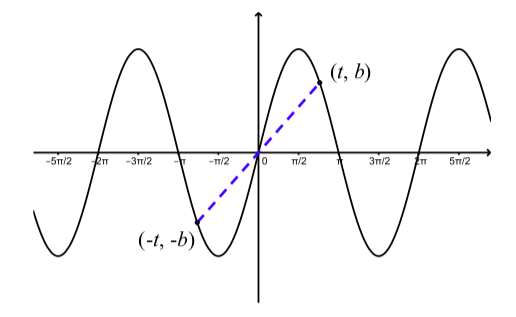
Figura\(\PageIndex{6}\): Gráfica que muestra la simetría de\(y = \sin(t)\).
Para ver mejor la simetría de la gráfica de la función sinusoidal, utilice el applet Geogebra Simetría de la Gráfica de\(y = \sin(t)\) en el siguiente enlace: http://gvsu.edu/s/Ou
Resumen
En esta sección, estudiamos los siguientes conceptos e ideas importantes:
- Las características importantes de las funciones sinusoidales de la forma\(y = A\sin(t)\) o\(y = A\cos(t)\) se muestran en la Tabla 2.1.
- La información en la Tabla 2.1 puede parecer mucho para recordar, y de hecho, en las siguientes secciones, obtendremos mucha más información sobre las ondas sinusoidales. Entonces, en lugar de tratar de recordar todo en la Tabla 2.1, es mejor recordar las formas básicas de las gráficas como se muestra en Figura\(\PageIndex{7}\) y Figura\(\PageIndex{8}\).
| \(y = A\sin(t)\) | \(y = A\cos(t)\) | |
|---|---|---|
| \ (y = A\ sin (t)\) ">Todos los números reales | dominio | \ (y = A\ cos (t)\) ">Todos los números reales |
| \ (y = A\ sin (t)\) ">\(2\pi\) | periodo | \ (y = A\ cos (t)\) ">\(2\pi\) |
| \ (y = A\ sin (t)\) ">\(|A|\) | amplitud | \ (y = A\ cos (t)\) ">\(|A|\) |
| \ (y = A\ sin (t)\) ">\((0, 0)\) | \(y\)-interceptar | \ (y = A\ cos (t)\) ">\((0, A)\) |
| \ (y = A\ sin (t)\) ">\(t = 0\) y\(t = \pi\) | \(t\)-interceptar en\([0, 2\pi)\) | \ (y = A\ cos (t)\) ">\(t = \dfrac{\pi}{2}\) y\(t = \dfrac{3\pi}{2}\) |
| \ (y = A\ sin (t)\) ">\(|A|\) | valor máximo | \ (y = A\ cos (t)\) ">\(|A|\) |
| \ (y = A\ sin (t)\) ">\(-|A|\) | valor mínimo | \ (y = A\ cos (t)\) ">\(-|A|\) |
| \ (y = A\ sin (t)\) ">El intervalo\([-|A|, |A|]\) | gama | \ (y = A\ cos (t)\) ">El intervalo\([-|A|, |A|]\) |
| \ (y = A\ sin (t)\) ">\(t = \dfrac{\pi}{2}\) | cuando\(A > 0\), el máximo ocurre en | \ (y = A\ cos (t)\) ">\(t = 0\) |
| \ (y = A\ sin (t)\) ">\(t = \dfrac{3\pi}{2}\) | cuando\(A > 0\), el máximo ocurre en | \ (y = A\ cos (t)\) ">\(t = \pi\) |
| \ (y = A\ sin (t)\) ">\(t = \dfrac{3\pi}{2}\) | cuando\(A < 0\), el máximo ocurre en | \ (y = A\ cos (t)\) ">\(t = \pi\) |
| \ (y = A\ sin (t)\) ">\(t = \dfrac{\pi}{2}\) | cuando\(A < 0\), el máximo ocurre en | \ (y = A\ cos (t)\) ">\(t = 0\) |
| \ (y = A\ sin (t)\) ">el origen | simetría con respecto a | \ (y = A\ cos (t)\) ">el\(y\) eje |
- Una forma de recordar la ubicación de las marcas de marca en el\(t\) eje es recordar que el espaciado para estas marcas es un cuarto de período y el período es\(2\pi\). Entonces el espaciado\(\dfrac{2\pi}{4} = \dfrac{\pi}{2}\).
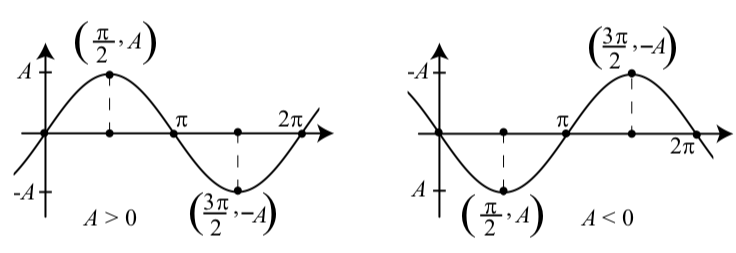
Figura\(\PageIndex{7}\): Gráficas de\(y = A\sin(t)\).
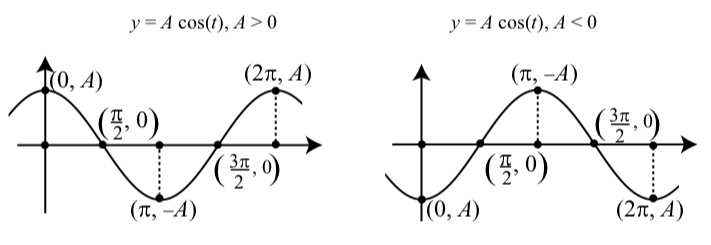
Figura\(\PageIndex{8}\): Gráficas de\(y = A\cos(t)\).
Material suplementario: funciones pares e impares
Hay un contexto matemático más general para este tipo de simetría, y eso tiene que ver con lo que se llaman funciones pares y funciones impares.
Definiciones: funciones pares e impares
- Una función\(f\) es una función par si\(f(-x) = f(x)\) para todos\(x\) en el dominio de\(f\).
- Una función\(f\) es una función impar si\(f(-x) = -f(x)\) para todos\(x\) en el dominio de\(f\).
Entonces con estas definiciones, podemos decir que la función coseno es una función par y la función seno es una función impar. ¿Por qué utilizamos estos términos? Una explicación es que los conceptos de funciones pares y funciones impares se utilizan para describir funciones\(f\) de la forma\(f(x) = x^n\) para algún entero positivo\(n\), y las gráficas de estas funciones exhiben diferentes tipos de simetría cuando\(n\) es par versus cuando\(n\) es impar.
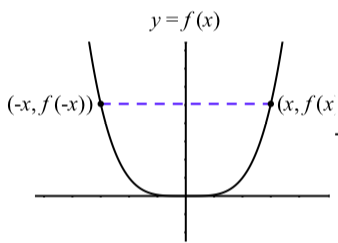
Figura\(\PageIndex{9}\):\(f(x) = x^n\), n par y\(f(-x) = f(x)\)
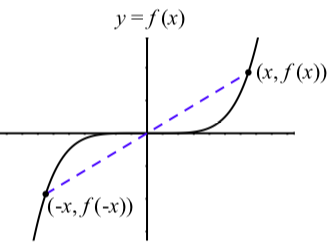
Figura\(\PageIndex{10}\):\(f(x) = x^n\),\(n\) impar y\(f(-x) = -f(x)\).
En Figura\(\PageIndex{9}\), vemos que cuando\(n\) es par,\(f(-x) = f(x)\) ya que\((-x)^n = x^n\). Entonces la gráfica es simétrica alrededor del\(y\) eje -eje. Cuando\(n\) es impar como en la Figura\(\PageIndex{10}\),\(f(-x) = -f(x)\) ya que\((-x)^n = -x^n\). Entonces la gráfica es simétrica sobre el origen. Es por esto que usamos el término funciones pares para aquellas funciones\(f\) para las cuales\(f(-x) = f(x)\), y usamos el término funciones impares para esas funciones para las cuales\(f(-x) = -f(x)\).


