2.2: Gráficas de Funciones Sinusoidales

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

Dejar\(A, B, C\), y\(D\) ser constantes con\(B > 0\) y considerar la gráfica de\(f(t) = A\sin(B(t - C)) + D\) o\(f(t) = A\cos(B(t - C)) + D\).

• ¿Cómo\(A\) afecta el valor de la gráfica de\(f\)? ¿Cómo se relaciona A con la amplitud de\(f\)?
• ¿Cómo\(B\) afecta el valor de la gráfica de\(f\)? ¿Cómo se relaciona B con el periodo de\(f\)?
• ¿Cómo\(C\) afecta el valor de la gráfica de\(f\)?
• ¿Cómo\(D\) afecta el valor de la gráfica de\(f\)?
• ¿Qué hace un desplazamiento de fase a una gráfica de seno o coseno? ¿Cómo reconocemos un desplazamiento de fase a partir de la ecuación de la sinusoide?
• ¿Cómo dibujamos con precisión la gráfica de\(f(t) = A\sin(B(t - C)) + D\) o\(f(t) = A\cos(B(t - C)) + D\) sin calculadora y cómo describimos correctamente los efectos de las constantes\(A, B, C\), y\(D\) en la gráfica?

Actividad de inicio

En esta sección, estudiaremos las gráficas de funciones cuyas ecuaciones son\(f(t) = A\sin(B(t - C)) + D\) y\(f(t) = A\cos(B(t - C)) + D\) dónde\(A, B, C\), y\(D\) son números reales. Estas funciones se denominan funciones sinusoidales y sus gráficas se denominan ondas sinusoidales. Primero nos centraremos en funciones cuyas ecuaciones son\(y = \sin(Bt)\) y\(y = \cos(Bt)\). Ahora completa la Parte 1 o la Parte 2 de esta actividad inicial.

Parte 1 — Uso de un applet de Geogebra

Para comenzar nuestra exploración, utilizaremos un applet de Geogebra llamado Period of a Sinusoid. La dirección web de este applet es http://gvsu.edu/s/LY

Después de abrir el applet, observe que hay un cuadro de entrada en la parte superior de la pantalla donde puede ingresar una función. Por ahora, deja este set en\(g(t) = \sin(t)\). Se debe mostrar el gráfico de la función sinusoidal. El deslizador en la parte superior se puede utilizar para cambiar el valor de B. Cuando esto se hace, se\(y = A\sin(t)\) mostrará la gráfica de para el valor actual de B junto con la gráfica de\(y = \sin(t)\).

1. Utilice el control deslizante para cambiar el valor de B. Explique en detalle la diferencia entre la gráfica de\(y = g(t) = \sin(t)\) y\(y = f(t) = \sin(Bt)\) para una constante\(B > 0\). Presta mucha atención a las gráficas y determina el periodo cuando\[(a)B = 2 \space (b) B = 3\space (c) B = 4 \space(d) B = 0.5\]. En particular, ¿de qué manera\(y = \sin(Bt)\) parece depender el periodo de\(B\)? Nota: Considera hacer dos casos separados: uno cuando\(B > 1\) y el otro cuando\(0< B <1\).
2. Ahora haga clic en el botón de reinicio en la esquina superior derecha de la pantalla. Esto restablecerá el valor de la B a su configuración inicial de\(B = 1\).
3. Cambie la función a\(g(t) = \cos(t)\) y repita la parte (1) para la función coseno. ¿El cambio del valor de B afecta a la gráfica\(y = \cos(Bt)\) de la misma manera que cambiar el valor para B afecta a la gráfica de\(t = \sin(Bt)\)?

Parte 2: Uso de una utilidad de gráficos

Asegúrese de que su utilidad gráfica esté establecida en modo radianes. Nota: La mayoría de las utilidades gráficas requieren el uso de\(x\) (o\(X\)) como la variable independiente (entrada) para una función. Utilizaremos\(x\) para la variable independiente cuando discutamos el uso de una utilidad gráfica.

1. Primero examinaremos la gráfica de\(y = \sin(Bx)\) para tres valores diferentes de\(B\). Grafica las tres funciones:\[y = \sin(x) \space\space y = \sin(2x) \space\space y = \sin(4x)\] usando los siguientes ajustes para la ventana de visualización:\(0 \leq x \leq 4\pi\) y\(-1.5 \leq y \leq 1.5\). Si es posible en su utilidad de gráficos, configúrela de manera que las marcas en el eje x estén espaciadas en\(\dfrac{\pi}{2}\) las unidades. Examine estas gráficas de cerca y determine el período para cada onda sinusoidal. En particular, ¿de qué manera\(y = \sin(Bx)\) parece depender el periodo de\(B\)?
2. Despeja la pantalla gráfica. Ahora examinaremos la gráfica de\(y = \sin(Bx)\) para tres valores diferentes de\(B\). Grafique las siguientes tres funciones:\[y = \sin(x) \space\space y = \sin(\dfrac{1}{2}x) \space\space y = \sin(\dfrac{1}{4}x)\] usando los siguientes ajustes para la ventana de visualización:\(0 \leq x \leq \pi\) y\(-1.5 \leq y \leq 1.5\) Si es posible en su utilidad de gráficos, configúrela de manera que las marcas en el eje x estén espaciadas en\(\dfrac{\pi}{2}\) unidades. Examine estas gráficas de cerca y determine el período para cada onda sinusoidal. En particular, ¿cómo el periodo de\(y = \sin(Bx)\) parece depender de B?
3. ¿Cómo\(y = \sin(Bx)\) aparece la gráfica de estar relacionada con la gráfica de\(y = \sin(x)\). Nota: Considera hacer dos casos separados: uno cuando\(B > 1\) y el otro cuando\(0 < B < 1\).

El Periodo de una Sinusoide

Cuando discutimos una expresión como\(\sin(t)\) o\(\cos(t)\), a menudo nos referimos a la expresión dentro de los paréntesis como el argumento de la función. En la actividad inicial, examinamos situaciones en las que el argumento era\(Bt\) para algún número\(B\). También vimos que este número afecta el periodo de la sinusoide. Si examinamos las gráficas lo suficientemente cerca, vimos que el periodo de\(y = \sin(Bt)\) y\(y = \cos(Bt)\) es igual a\(\dfrac{2\pi}{B}\). Los gráficos de la Figura 2.11 ilustran esto.

Observe que la gráfica de\(y = \sin(2t)\) tiene un ciclo completo sobre el intervalo\([0, \pi]\) y así lo es su periodo\(\pi = \dfrac{2\pi}{2}\). La gráfica de\(y = \sin(4t)\) tiene un ciclo completo a lo largo del intervalo\([0, \dfrac{\pi}{2}]\) y así lo es su periodo\(\dfrac{\pi}{2} = \dfrac{2\pi}{4}\). En estos dos casos, tuvimos\(B > 1 \) en\(y = \sin(Bt)\). ¿Obtenemos el mismo resultado cuando\(0 < B < 1\)? La Figura 2.12 muestra gráficas para\(y = \sin(\dfrac{1}{2}t)\) y\(y = \sin(\dfrac{1}{4}t)\)?

Observe que la gráfica de\(y = \sin(\dfrac{1}{2}t)\) tiene un ciclo completo a lo largo del intervalo\([0, 4\pi]\)

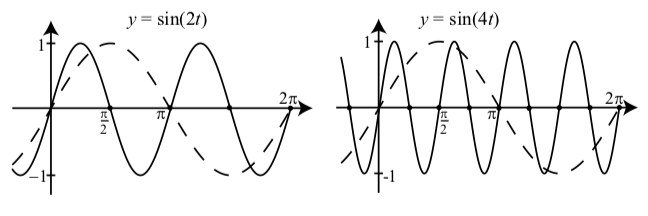
Figura\(\PageIndex{1}\): Gráficas de\(y = \sin(2t)\) y\(y = \sin(4t)\). También\(y = \sin(t)\) se muestra la gráfica de (guiones).

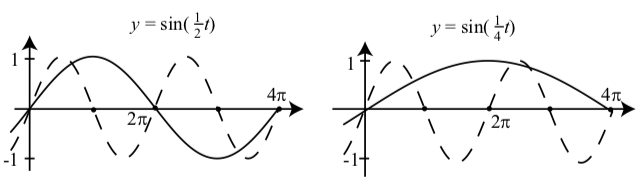
Figura\(\PageIndex{2}\): Gráficas de\(y = \sin(\dfrac{1}{2}t)\) y\(y = \sin(\dfrac{1}{4}t)\). También\(y = \sin(t)\) se muestra la gráfica de (guiones).

El periodo de\(y = \sin(\dfrac{1}{2}t)\) es\(4\pi = \dfrac{2\pi}{\dfrac{1}{2}}\).

La gráfica de\(y = \sin(\dfrac{1}{4}t)\) tiene la mitad de un ciclo completo sobre el intervalo\([0, 4\pi]\) y así el periodo de\(y = \sin(\dfrac{1}{4}t)\) es\(8\pi = \dfrac{2\pi}{\dfrac{1}{4}}\).
Una buena pregunta ahora es: “¿Por qué son los periodos de\(y = \sin(Bt)\) e\(y = \cos(Bt)\) iguales a\(\dfrac{2\pi}{B}\)?” La idea es que cuando multiplicamos la variable independiente\(t\) por una constante\(B\), puede cambiar la entrada que necesitamos para obtener una salida específica. Por ejemplo, la entrada de\(t = 0\) in\(y = \sin(t)\) y\(y = \sin(Bt)\) produce la misma salida. Para completar un periodo en\(y = \sin(Bt)\) necesitamos pasar por intervalo de longitud\(2\pi\) para que nuestra entrada sea\(2\pi\). No obstante, para que el argumento\((Bt)\) en\(y = \sin(Bt)\) sea\(2\pi\), necesitamos\(Bt = 2\pi\) y si resolvemos esto por\(t\), obtenemos\(t = \dfrac{2\pi}{B}\). Entonces la función dada por\(y = \sin(Bt)\) (o\(y = \cos(Bt)\)) completará un ciclo completo cuando\(t\) varíe de\(t = 0\) a\(t = \dfrac{2\pi}{B}\), y por lo tanto, el periodo es\(\dfrac{2\pi}{B}\). Observe que si usamos\(y = A\sin(Bt)\) o\(y = A\cos(Bt)\), el valor de A solo afecta la amplitud de la sinusoide y no afecta el periodo.

Si\(A\) es un número real y\(B\) es un número real positivo, entonces el periodo de las funciones dadas por\(y = A\sin(Bt)\) y\(y = A\cos(Bt)\) es\(\dfrac{2\pi}{B}\).

Ejercicio\(\PageIndex{1}\)

1. Determinar la amplitud y periodo de las siguientes funciones sinusoidales.:\[(a) y = 3\cos(\dfrac{1}{3}t)\]\[(b) y = -2\sin(\dfrac{\pi}{2}t)\]
2. La gráfica a continuación es una gráfica de una función sinusoidal. Determinar una ecuación para esta función.

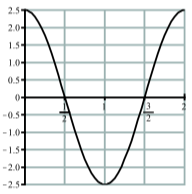
Contestar

1. (a) Porque\(y = 3\cos(\dfrac{1}{3}t)\), la amplitud es\(3\) y el periodo es\(\dfrac{2\pi}{\dfrac{1}{3}} = 6\pi\)

(b) Porque\(y = -2\sin(\dfrac{\pi}{2}t)\), la amplitud es\(2\) y el periodo es\(\dfrac{2\pi}{\dfrac{pi}{2}} = 4\).

2. De la gráfica, la amplitud es\(2.5\) y el periodo es\(2\). Usando una función coseno, tenemos\(A = 2.5\) y\(\dfrac{2\pi}{B} = 2\). Resolviendo para\(B\) da\(B = \pi\). Entonces una ecuación es\(y = 2.5\cos(\pi t)\).

Desplazamiento de fase

Ahora investigaremos el efecto de restar una constante del argumento (variable independiente) de una función circular. Es decir, investigaremos qué efecto\(C\) tiene el valor de un número real la gráfica de\(y = \sin(t - C)\) y\(y = \cos(t - C)\).

Actividad 2.10 (La Gráfica de\(y = \sin(t - C)\))

Completa la Parte 1 o la Parte 2 de esta actividad.

Parte 1 — Uso de un applet de Geogebra

Usaremos un applet de Geogebra llamado Sinusoid — Phase Shift. La dirección web de este applet es http://gvsu.edu/s/Mu

Después de abrir el applet, observe que hay un cuadro de entrada en la parte superior de la pantalla donde puede ingresar una función. Por ahora, deja este set en\(g(t) = \sin(t)\). Se debe mostrar el gráfico de la función sinusoidal. El deslizador en la parte superior se puede utilizar para cambiar el valor de C. Cuando esto se hace, se\(y = A\sin(t - C)\) mostrará la gráfica de para el valor actual de C junto con la gráfica de\(y = \sin(t)\).

1. Utilice el control deslizante para cambiar el valor de\(C\). Explique en detalle la diferencia entre la gráfica de\(y = g(t) = \sin(t)\) y\(y = f(t) = \sin(t - C)\) para una constante C. Preste mucha atención a las gráficas y determine el desplazamiento horizontal cuando\[(a) C=1\space (b) C=2\space(c) C=3\space (d) C=-1\space (e) C=-2\space (f) C=-3.\] En particular, describa la diferencia entre la gráfica de\(y = \sin(t - C)\) y la gráfica de\(y = \sin(t)\)? Nota: Considera hacer dos casos separados: uno cuando\(C >0\) y el otro cuando\(C < 0\).
2. Ahora haga clic en el botón de reinicio en la esquina superior derecha de la pantalla. Esto restablecerá el valor de la C a su configuración inicial de\(C = 0\).
3. Cambie la función a\(g(t) = \cos(t)\) y repita la parte (1) para la función coseno. ¿El cambio del valor de C afecta a la gráfica de\(y = \cos(t - C)\) afecta a la onda sinusoidal de la misma manera que cambiar el valor para C afecta a la gráfica de\(y = \sin(t - C)\)?

Parte 2: Uso de una utilidad de gráficos

Asegúrese de que su utilidad gráfica esté establecida en modo radianes.

1. Primero examinaremos la gráfica de\(y = \sin(t - C)\) para dos valores diferentes de\(C\). Grafica las tres funciones:\[y = \sin(x) \space y = \sin(x - 1) \space y = \sin(x - 2)\] usando los siguientes ajustes para la ventana de visualización:\(0 \leq x \leq 4\pi\) y\(-1.5 \leq y \leq 1.5\). Examine estas gráficas de cerca y describa la diferencia entre la gráfica de\(y = \sin(x - C)\) y la gráfica de\(y = \sin(x)\) para estos valores de C.
2. Despeja la pantalla gráfica. Ahora examinaremos la gráfica de\(y = \sin(x - C)\) para dos valores diferentes de C. Grafique las siguientes tres funciones:\[y = \sin(x)\]\[y = \sin(x + 1) = \sin(x-(-1))\]\[y = \sin(x)\]\[y = \sin(x + 2) = \sin(x-(-2))\] usando los siguientes ajustes para la ventana de visualización:\(0 \leq x \leq \pi\) y\(-1.5 \leq y \leq 1.5\). Examine estas gráficas de cerca y describa la diferencia entre la gráfica de\(y = \sin(t - C)\) y la gráfica de\(y = \sin(t)\) para estos valores de C.
3. Describir la diferencia entre la gráfica de\(y = \sin(x - C)\) y la gráfica de\(y = \sin(x)\)? Nota: Considera hacer dos casos separados: uno cuando\(C > 0\) y el otro cuando\(C < 0\).

Al explorar las gráficas en la Actividad 2.10, debemos notar que cuando\(C > 0\), la gráfica de\(y = \sin(t - C)\) es la gráfica de traducida\(y = \sin(t)\) horizontalmente a la derecha por unidades C. De manera similar, la gráfica de\(y = \cos(t - C)\) es la gráfica de traducida\(y = \cos(t)\) horizontalmente a la derecha por unidades C. Cuando se trabaja con una gráfica sinusoidal, dicha traslación horizontal se denomina desplazamiento de fase. Esto se ilustra en la Figura 2.13, que muestra las gráficas de\(y = \sin(t)\) y\(y = \sin(t - \dfrac{\pi}{2})\). Para referencia, también\(y = \sin(t)\) se muestra la gráfica de.

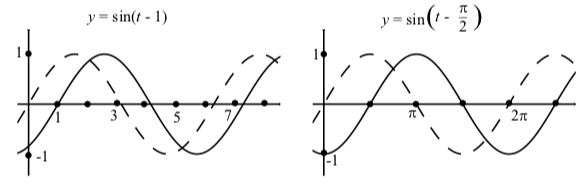
Figura\(\PageIndex{3}\): Gráficas de\(y = \sin(t - 1)\) y\(y = \sin(t - \dfrac{\pi}{2})\). También\(y = \sin(t)\) se muestra la gráfica de (guiones).

Entonces, ¿por qué estamos viendo este cambio de fase? La razón es que la gráfica de\(y = \sin(t)\) pasará por un ciclo completo a lo largo del intervalo definido por\(0 \leq t \leq 2\pi\). De igual manera, la gráfica de\(y = \sin(t - C)\) pasará por un ciclo completo a lo largo del intervalo definido por\(0 \leq t - C \leq 2\pi\). Resolviendo para\(t\), vemos eso\(C \leq t \leq 2\pi + C\). Entonces vemos que este ciclo para\(y = \sin(t)\) ha sido desplazado por unidades C.

Este argumento también funciona cuando\(C < 0\) y cuando usamos la función coseno en lugar de la función seno. La Figura 2.14 ilustra esto con\(y = \cos(t - (-1))\) y\(y = \cos(t - (-\dfrac{\pi}{2}))\). Observe que podemos reescribir estas dos ecuaciones de la siguiente manera:\[y = \cos(t - (-1))\]\[y = \cos(t + 1))\]\[y = \cos(t - (-\dfrac{\pi}{2}))\]\[y = \cos(t + \dfrac{\pi}{2})\]

Resumimos los resultados para el cambio de fase de la siguiente manera:

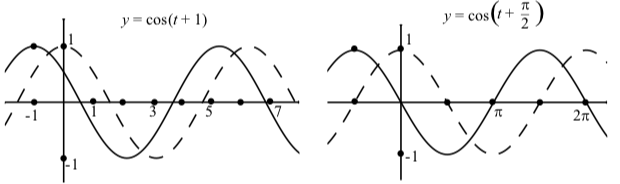
Figura\(\PageIndex{4}\): Gráficas de\(y = \cos(t + 1))\) y\(y = \cos(t + \dfrac{\pi}{2})\). También\[y = \cos(t)\] se muestra la gráfica de (guiones).

Para\(y = \sin(t - C)\) y\(y = \cos(t - C)\), donde C es cualquier número real distinto de cero:

• La gráfica de\(y = \sin(t)\) (o\(y = \cos(t)\)) se desplaza horizontalmente\(|C|\) unidades. A esto se le llama el desplazamiento de fase de la sinusoide.
• Si\(C > 0\), la gráfica de\(y = \sin(t)\) (o\(y = \cos(t)\)) se desplaza horizontalmente unidades C hacia la derecha. Es decir, hay un desplazamiento de fase de las unidades C a la derecha.
• Si\(C < 0\), la gráfica de\(y = \sin(t)\) (o\(y = \cos(t)\)) se desplaza horizontalmente unidades C hacia la izquierda. Es decir, hay un desplazamiento de fase de unidades C a la izquierda.

Ejercicio\(\PageIndex{2}\)

1. Determinar la amplitud y el desplazamiento de fase de las siguientes funciones sinusoidales. \[(a) y = 3.2(\sin(t - \dfrac{\pi}{3})) \]\[(b) y = 4\cos(t + \dfrac{\pi}{6})\]
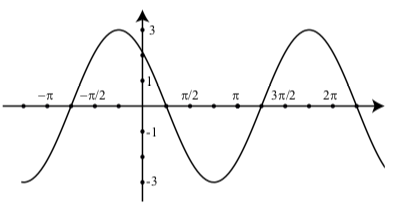
2. El siguiente gráfico es un gráfico de una función sinusoidal (a) Determinar una ecuación para esta función. (b) Determinar una segunda ecuación para esta función.

Contestar

1. (a) For\(y = 3.2(\sin(t - \dfrac{\pi}{3}))\), la amplitud es\(3.2\) y el desplazamiento de fase es\(\dfrac{\pi}{3}\)
(b) For\(y = 4\cos(t + \dfrac{\pi}{6})\), note que\(y = 4\cos(t - (-\dfrac{\pi}{6}))\). Entonces la amplitud es\(4\) y el desplazamiento de fase es\(-\dfrac{\pi}{6}\).

2. Existen varias ecuaciones posibles para esta sinusoide. Algunas de estas ecuaciones son:

\[y = 3\sin(t + \dfrac{3\pi}{4})\]

\[y = -3\sin(t - \dfrac{\pi}{4})\]

\[y = 3\cos(t + \dfrac{\pi}{4})\]

\[y = -3\cos(t - \dfrac{3\pi}{4})\]

Se puede utilizar una utilidad gráfica para verificar que cualquiera de estas ecuaciones produzca la gráfica dada.

Desplazamiento vertical

Tenemos una transformación más de una sinusoide para explorar, el llamado desplazamiento vertical. Esta es una mediante la adición de una constante a la ecuación para una sinusoide y se explora en la siguiente actividad.

Actividad 2.12 (El desplazamiento vertical de una sinusoide)

Completa la Parte 1 o la Parte 2 de esta actividad.

Parte 1 — Uso de un applet de Geogebra

Ahora investigaremos el efecto de agregar una constante a una función sinusoidal. Es decir, investigaremos qué efecto\(D\) tiene el valor de un número real la gráfica de\(y = A\sin(B(t - C)) + D\) y\(y = A\cos(B(t - C)) + D\). Completa la Parte 1 o la Parte 2 de esta actividad. Usaremos un applet de Geogebra llamado Exploring a Sinusoid. La dirección web de este applet es http://gvsu.edu/s/LX

Después de abrir el applet, observe que hay un cuadro de entrada en la parte superior de la pantalla donde puede ingresar una función. Por ahora, deja este set en\(g(t) = \sin(t)\). Se debe mostrar el gráfico de la función sinusoidal. Hay cuatro deslizadores en la parte superior que se pueden utilizar para cambiar los valores de\(A, B, C\), y\(D\).

1. Deja los valores\(A = 1, B = 1\) y\(C = 0\) establece. Utilice el control deslizante de D para cambiar el valor de C. Cuando esto se haga, se\(y = \sin(t) + D\) mostrará la gráfica de para el valor actual de D junto con la gráfica de\(y = \sin(t)\).

(a) Use el control deslizante para cambiar el valor de D. Explique en detalle la diferencia entre la gráfica de\(y = g(t) = \sin(t)\) y\(y = f(t) = \sin(t) + D\) para una constante D. Preste mucha atención a las gráficas y determine el desplazamiento vertical cuando\[i. D = 1.\]\[ii. D = 2.\]\[iii. D = 3.\]\[iv. D = -1.\]\[v. D = -2.\]\[vi. D = -3.\] En particular, describa la diferencia entre la gráfica de\(y = \sin(t) + D\) y la gráfica de\(y = \sin(t)\)? Nota: Considera hacer dos casos separados: uno cuando\(D > 0\) y el otro cuando\(D < 0\).

(b) Ahora haga clic en el botón de reinicio en la esquina superior derecha de la pantalla. Esto restablecerá el valor de la C a su configuración inicial de\(C = 0\).

(c) Cambiar la función a\(g(t) = \cos(t)\) y repetir la parte (1) para la función coseno. ¿El cambio del valor de D afecta a la gráfica de\(y = \cos(t) + D\) afecta a la onda sinusoidal de la misma manera que cambiar el valor para D afecta a la gráfica de\(y = \sin(t) + D\)?

2. Ahora cambie el valor de A a 0.5, el valor de B a 2 y el valor de C a 0.5. El gráfico de\(g(t) = \cos(t)\) seguirá mostrándose pero ahora lo tendremos\(f(t) = 0.5\cos(2(t - 0.5)) + D\). ¿El cambio del valor de D afecta a la gráfica de\(y = 0.5\cos(2(t - 0.5)) + D\) afecta a la onda sinusoidal de la misma manera que cambiar el valor para D afecta a la gráfica de\(y = \cos(t)\)?

Parte 2: Uso de una utilidad de gráficos

Asegúrese de que su utilidad gráfica esté establecida en modo radianes.

1. Primero examinaremos la gráfica de\(y = \cos(t) + D\) para cuatro valores diferentes de\(D\). Grafica las cinco funciones:\[y = \cos(x)\]\[y = \cos(x) + 1\]\[y = \cos(x) - 1\]\[y = \cos(x) + 2\]\[y = \cos(x) - 2\] usando los siguientes ajustes para la ventana de visualización:\(0 \leq x \leq 2\pi\) y\(-3 \leq y \leq 3\). Examine estas gráficas de cerca y describa la diferencia entre la gráfica de\(y = \cos(x) + D\) y la gráfica de\(y = \cos(x)\) para estos valores de D.
2. Despeja la pantalla gráfica. Ahora examinaremos la gráfica de\(y = 0.5\cos(2(x - 0.5))\) para dos valores diferentes de\(D\). Grafique las siguientes tres funciones:\[y = 0.5\cos(2(x - 0.5))\]\[y = 0.5\cos(2(x - 0.5)) + 2\]\[y = 0.5\cos(2(x - 0.5)) - 2\] usando los siguientes ajustes para la ventana de visualización:\(0 \leq x \leq 2\pi\) y\(-3 \leq y \leq 3\). Examine estas gráficas de cerca y describa la diferencia entre la gráfica de\(y = 0.5\cos(2(x - 0.5)) + D\) y la gráfica de\(y = 0.5\cos(2(x - 0.5))\) para estos valores de\(D\).

Al explorar las gráficas en la Actividad 2.12, debemos notar que la gráfica de algo así como\(y = A\sin(B(t - C)) + D\) es la gráfica de las unidades\(y = A\sin(B(t - C))\) desplazadas hacia arriba cuando\(D > 0\) y\(D\) las unidades\(|D|\) desplazadas hacia abajo cuando\(D < 0\). Cuando se trabaja con una gráfica sinusoidal, dicha traslación vertical se denomina desplazamiento vertical. Esto se ilustra en la Figura 2.15 para una situación en la que\(D > 0\).

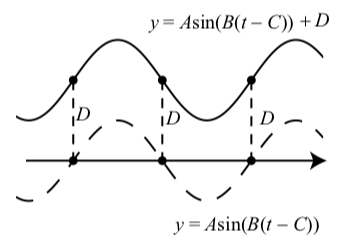
Figura\(\PageIndex{5}\): Gráficas de\(y = A\sin(B(t - C))\) (guiones) y\(y = A\sin(B(t - C)) + D\) (sólidos) para\(D > 0\).

El\(y\) eje -no se muestra en la Figura\(\PageIndex{5}\) porque ésta muestra una gráfica general con un desplazamiento de fase.

Lo que hemos hecho en la Actividad 2.12 es comenzar con una gráfica como por ejemplo\(y = A\sin(B(t - C))\) y sumar una constante a la variable dependiente para obtener\(y = A\sin(B(t - C)) + D\). Entonces, cuando t permanece igual, estamos agregando\(D\) a la variable dependiente. El efecto es traducir toda la gráfica hacia arriba por\(D\) unidades si\(D > 0\) y hacia abajo por\(|D|\) unidades si\(D < 0\).

Amplitud, Período, Desplazamiento de Fase y Desplazamiento Vertical

El siguiente es un resumen del trabajo que hemos realizado en esta sección que trata de amplitud, periodo, desplazamiento de fase y desplazamiento vertical para una función sinusoidal.

Dejar\(A, B, C\), y\(D\) ser números reales distintos de cero con\(B > 0\). Para\(y = A\sin(B(t - C)) + D\) y\(y = A\cos(B(t - C)) + D\)

La amplitud de la gráfica sinusoidal es\(|A|\).

• Si\(|A| > 1\), entonces hay un estiramiento vertical de la sinusoide pura por un factor de\(|A|\).
• Si\(|A| > 1\), entonces hay una contracción vertical de la sinusoide pura por un factor de\(|A|\).

El periodo de la gráfica sinusoidal es\(2\pi\).

• Cuando\(B > 1\), hay una compresión horizontal de las gráficas.
• Cuando\(0 < B < 1\), hay un tramo horizontal de la gráfica.

El desplazamiento de fase de la gráfica sinusoidal es\(|C|\).

• Si\(C > 0\), hay un desplazamiento horizontal de\(C\) unidades a la derecha.
• Si\(C < 0\), hay un desplazamiento horizontal de\(|C|\) unidades hacia la izquierda.

El desplazamiento vertical de la gráfica sinusoidal es\(|D|\).

• Si\(D > 0\), el desplazamiento vertical es\(D\) unidades hacia arriba.
• Si\(D < 0\), el desplazamiento vertical es\(|D|\) unidades hacia abajo.

Ejemplo\(\PageIndex{1}\): The Graph of a Sinusoid

Este ejemplo ilustrará cómo utilizar las características de una sinusoide y servirá de introducción a la discusión más general que sigue. La gráfica de\(y = 3\sin(4(t - \dfrac{\pi}{8})) + 2\) tendrá el siguiente aspecto: Observe que los ejes aún no han sido dibujados. Queremos exponer las coordenadas de los puntos\(P, Q, R, S\), y\(T\). Hay varias opciones pero haremos que el punto\(P\) sea lo más cercano posible al origen. Las siguientes son las características importantes de esta sinusoide:

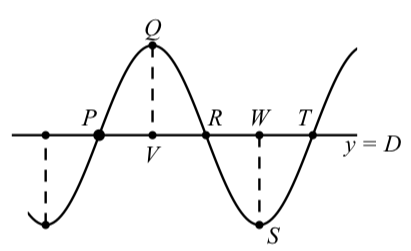
Figura\(\PageIndex{6}\): Gráfica de una sinusoide

• El desplazamiento de fase es\(\dfrac{\pi}{8}\).
• La amplitud es\(3\).
• El periodo es\(\dfrac{2\pi}{4} = \dfrac{\pi}{2}\)
• El desplazamiento vertical es\(2\).

Entonces, para la gráfica en Figura\(\PageIndex{6}\), podemos sacar las siguientes conclusiones.

• Dado que el desplazamiento vertical es\(2\), la línea horizontal que es la línea central de la sinusoide es\(y = 2\).
• Dado que el desplazamiento de fase es\(\dfrac{\pi}{8}\) y esta es una función sinusoidal, las coordenadas de\(P\) son\((\dfrac{\pi}{8}, 2)\).
• Ya que el periodo es\(\dfrac{\pi}{2}\), la\(t\) coordenada -de\(R\) es\(\dfrac{\pi}{8} + \dfrac{1}{2}(\dfrac{\pi}{2}) = \dfrac{3\pi}{8}\). Entonces las coordenadas de\(R\) son\((\dfrac{3\pi}{8}, 2)\).
• Ya que el periodo es\(\dfrac{\pi}{2}\), la\(t\) coordenada -de\(T\) es\(\dfrac{\pi}{8} + \dfrac{\pi}{2} = \dfrac{5\pi}{8}\). Entonces las coordenadas de\(R\) son\((\dfrac{5\pi}{8}, 2)\).
• Ya que el periodo es\(\dfrac{\pi}{2}\), la\(t\) coordenada -de\(Q\) es\(\dfrac{\pi}{8} + \dfrac{1}{4}(\dfrac{\pi}{2}) = \dfrac{\pi}{4}\) .También, dado que la amplitud es\(3\), la\(y\) -coordenada de\(Q\) es\(2 + 3 = 5\). Entonces las coordenadas de\(Q\) son\((\dfrac{\pi}{4}, 5)\).
• Ya que el periodo es\(\dfrac{\pi}{2}\), la\(t\) coordenada -de\(S\) es\(\dfrac{\pi}{8} + \dfrac{3}{4}(\dfrac{\pi}{2}) = \dfrac{\pi}{2}\) .También, dado que la amplitud es\(3\), la\(y\) -coordenada de\(S\) es\(2 - 3 = -1\). Entonces las coordenadas de\(S\) son\((\dfrac{\pi}{2}, -1)\).

Podemos verificar todos estos resultados mediante el uso de una utilidad gráfica para dibujar la gráfica de\(y = 3\sin(4(t - \dfrac{\pi}{8})) + 2\) usar\(0 \leq t \leq \dfrac{5\pi}{8}\) y\(-2\ leq y \leq 6\). Si la utilidad lo permite, establezca la escala t en un cuarto de período, que es\(\dfrac{\pi}{8}\).

Notas Importantes sobre los Sinusoides

• Para\(y = A\sin(B(t - C)) + D\) y\(y = A\cos(B(t - C)) + D\), la amplitud, el periodo, y el desplazamiento vertical serán los mismos.
• La gráfica para ambas funciones se verá como la que se muestra en la Figura\(\PageIndex{7}\). La diferencia entre\(y = A\sin(B(t - C)) + D\) y\(y = A\cos(B(t - C)) + D\) será el desplazamiento de fase.
• La línea horizontal mostrada no es el eje t. Es la línea horizontal\(y = D\), a la que a menudo llamamos la línea central para la sinusoide.

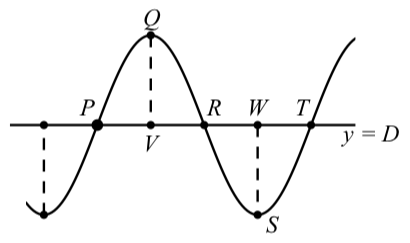
Figura\(\PageIndex{7}\): Gráfica de una sinusoide

Entonces, para usar los resultados sobre sinusoides y Figura\(\PageIndex{7}\), tenemos:

1. La amplitud, que llamaremos amp, es igual a las longitudes de los segmentos\(QV\) y\(WS\).

2. El periodo, al que llamaremos per, es igual a\(\dfrac{2\pi}{B}\). Además, la longitud de los segmentos\(PV,VR,RW\), y\(WT\) son iguales a\(\dfrac{1}{4} per\).
3. Para\(y = A\sin(B(t - C)) + D\), podemos usar el punto\(P\) para el desplazamiento de fase. Entonces la\(t\) coordenada -del punto\(P\) es\(C\) y\(P\) tiene coordenadas\((C, D)\). Podemos determinar las coordenadas de los otros puntos según sea necesario utilizando la amplitud y el periodo. Por ejemplo:

   El punto\(Q\) tiene coordenadas\((C + \dfrac{1}{4} per, D + amp)\)

   El punto\(R\) tiene coordenadas\((C + \dfrac{1}{2} per, D)\)

   El punto\(S\) tiene coordenadas\((C + \dfrac{3}{4} per, D - amp)\)

   El punto\(T\) tiene coordenadas\((C + per, D)\)

4. Para\(y = A\cos(B(t - C)) + D\), podemos usar el punto\(Q\) para el desplazamiento de fase. Entonces la\(t\) coordenada -del punto\(Q\) es\(C\) y\(Q\) tiene coordenadas\((C, D + amp)\). Podemos determinar las coordenadas de los otros puntos según sea necesario utilizando la amplitud y el periodo. Por ejemplo:

   El punto\(P\) tiene coordenadas\((C - \dfrac{1}{4} per, D)\)

   El punto\(R\) tiene coordenadas\((C + \dfrac{1}{4} per, D)\)

5. El punto\(S\) tiene coordenadas\((C + \dfrac{1}{2} per, D - amp)\)

   El punto\(T\) tiene coordenadas\((C + \dfrac{3}{4} per, D)\)

Tenga en cuenta que no es necesario tratar de recordar todos los hechos en los ítems (3) y (4). Lo que debemos recordar es cómo utilizar los conceptos de un cuarto de período y la amplitud ilustrada en los ítems (3) y (4). Esto se hará en las próximas dos comprobaciones de avance, que en realidad son ejemplos guiados.

Ejercicio\(\PageIndex{3}\)

Las características de una sinusoide pueden ser útiles para establecer una ventana de visualización adecuada cuando se produce un gráfico útil de una sinusoide en una utilidad gráfica. Esto es especialmente cierto cuando el periodo es pequeño o grande. Por ejemplo, considere la función sinusoidal\[y = 6.3\cos(50\pi(t + 0.01)) + 2\]

1. ¿Cuál es la amplitud?

2. ¿Cuál es el cambio de fase?

3. ¿Cuál es el periodo?

4. ¿Cuál es el desplazamiento vertical?

5. Utilice esta información para determinar las coordenadas para el punto\(Q\) en el siguiente diagrama.

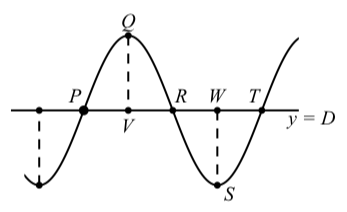
6. Ahora determinar las coordenadas de los puntos\(P, R, S\), y\(T\).

7. Utilice esta información y una utilidad gráfica para dibujar una gráfica de (un poco más de) un periodo de esta sinusoide que muestre los puntos\(P, Q\), y\(T\).

Contestar

1. La amplitud es\(6.3\).
2. El periodo es\(\dfrac{2\pi}{50\pi} = \dfrac{1}{25}\)
3. Escribimos\(y = 6.3\cos(50\pi(t - (-0.01))) + 2\) y vemos que el desplazamiento de fase es\(-0.01\) o\(0.01\) unidades a la izquierda.
4. El desplazamiento vertical es\(2\).
5. Debido a que estamos usando un coseno y el desplazamiento de fase es\(-0.01\), podemos usar\(-0.01\) como la\(t\) coordenada de\(Q\). La\(y\) coordenada -será el desplazamiento vertical más la amplitud. Entonces la\(y\) -coordenada es\(8.3\). El punto\(Q\) tiene coordenadas\((-0.01, 8.3)\)
6. Ahora utilizamos el hecho de que la distancia horizontal entre\(P\) y\(Q\) es de un cuarto de período. Ya que el periodo es\(\dfrac{1}{25} = 0.04\), vemos que un cuarto de periodo lo es\(0.01\). El punto\(P\) también se encuentra en la línea central, que es\(y = 2\). Entonces las coordenadas de\(P\) son\((-0.02, 2)\).

Ahora utilizamos el hecho de que la distancia horizontal entre\(Q\) y\(R\) es de un cuarto de período. El punto\(R\) está en la línea central de la sinusoide y así lo\(R\) ha hecho las coordenadas\((0, 2)\).

El punto\(S\) es un punto bajo en la sinusoide. Entonces su\(y\) -coordenada será\(D\) menos la amplitud, que es\(2 - 6.3 = -4.3\). Utilizando el hecho de que la distancia horizontal de\(R\) a\(S\) es de un cuarto de período, las coordenadas de\(S\) son\((0.01, -4.3)\). Dado que el punto\(T\) está en la línea central y la distancia horizontal de\(S\) a\(T\) es de un cuarto de período, las coordenadas de\(T\) son\((0.03, 2)\).

7. Utilizaremos una ventana de visualización que esté un cuarto de período a la izquierda\(P\) y un cuarto de período a la derecha de\(T\). Entonces usaremos\ (-0.03

leq t\ leq 0.03\). Ya que el valor máximo es\(8.3\) y el valor mínimo es\(-4.3\), vamos a utilizar\(-5 \leq y \leq 9\).

Ejercicio\(\PageIndex{4}\)

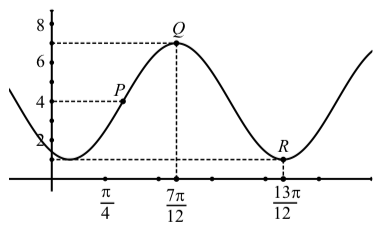
Determinaremos dos ecuaciones para la sinusoide mostrada en la Figura\(\PageIndex{8}\).

1. Determinar las coordenadas de los puntos\(Q\) y\(R\). La distancia vertical entre estos dos puntos es igual a dos veces la amplitud. Utilice las coordenadas y de estos puntos para determinar dos veces la amplitud y luego la amplitud.
2. La línea central para la sinusoide está a medio camino entre el punto alto\(Q\) y el punto bajo\(R\). Utilice las coordenadas\(Q\) y de y\(R\) para determinar la línea central\(y = D\). Este será el desplazamiento vertical.

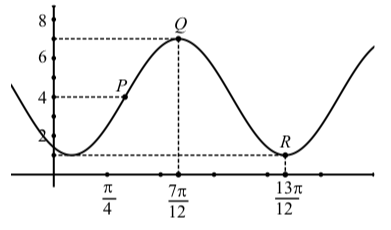
Figura\(\PageIndex{8}\): El gráfico de una sinusoide

3. La distancia horizontal entre\(Q\) y\(R\) es igual a la mitad de un período. Utilice las coordenadas t de\(Q\) y\(R\) para determinar la longitud de la mitad de un período y por lo tanto, el período. Utilice esto para determinar el valor de\(B\).
4. Ahora encontraremos una ecuación de la forma\(y = A\cos(B(t - C)) + D\). Todavía necesitamos el cambio de fase\(C\). Utilice el punto\(Q\) para determinar el desplazamiento de fase y por lo tanto, el valor de\(C\). Ahora tenemos valores para\(A, B, C\), y\(D\) para la ecuación\(y = A\cos(B(t - C)) + D\).
5. Para determinar una ecuación de la forma\(y = A\sin(B(t - C')) + D\)., utilizaremos el punto\(P\) para determinar el desplazamiento de fase\(C'\). (Se utilizó un símbolo diferente porque\(C'\) será diferente que\(C\) en la parte (4).) Observe que la coordenada y de\(P\) es 4 y así\(P\) se encuentra en la línea central. Podemos utilizar el hecho de que la distancia horizontal entre P y\(Q\) es igual a un cuarto de período. Determinar la coordenada t de\(P\), que será igual a\(C'\). Ahora escribe la ecuación\(y = A\sin(B(t - C')) + D\). usando los valores de\(A, B, C'\), y\(D\) que hemos determinado.

Podemos verificar las ecuaciones que encontramos en las partes (4) y (5) graficando estas ecuaciones usando una utilidad gráfica.

Contestar

1. Las coordenadas de\(Q\) son\((\dfrac{7\pi}{12}, 7)\) y las coordenadas de\(R\) son\((\dfrac{13\pi}{12}, 1)\). Entonces dos veces la amplitud es\(7 - 1 = 6\) y la amplitud es\(3\).

2. Agregamos la amplitud al\(y\) valor más bajo para determinar\(D\). Esto da\(D = 1 + 3 = 4\) y la línea central es\(y = 4\).

3. La distancia horizontal entre\(Q\) y\(R\) es\(\dfrac{13\pi}{12} - \dfrac{7\pi}{12} = \dfrac{6\pi}{12}\). Entonces vemos que la mitad de un periodo es\(\dfrac{\pi}{2}\) y el periodo lo es\(\pi\). Entonces\(B = \dfrac{2\pi}{\pi} = 2\).

4. Para\(y = A\cos(B(t - c)) + D\), podemos usar el punto\(Q\) para determinar un desplazamiento de fase de\(\dfrac{7\pi}{12}\). Entonces una ecuación para esta sinusoide es\[y = 3\cos(2(t - \dfrac{7\pi}{12})) + 4.\]

5. El punto\(P\) está en la línea central y por lo tanto la distancia horizontal entre\(P\) y\(Q\) es un cuarto de período. Entonces esta distancia horizontal es\(\dfrac{\pi}{4}\) y la\(t\) -coordenada de\(P\) es\[\dfrac{7\pi}{12} - \dfrac{\pi}{4} = \dfrac{4\pi}{12} = \dfrac{\pi}{3}.\]
Esto puede ser el desplazamiento de fase para\(y = A\sin(B(t - C')) + D\). Entonces otra ecuación para esta sinusoide es\[y = 3\sin(2(t - \dfrac{\pi}{3})) + 4\]

Resumen

En esta sección, estudiamos los siguientes conceptos e ideas importantes: Para una función sinusoidal de la forma\(f(t) = A\sin(B(t - C)) + D\) o\(f(t) = A\cos(B(t - C)) + D\) dónde\(A, B, C\), y\(D\) son números reales con\(B > 0\):

• El valor de\(|A|\) es la amplitud de la función sinusoidal.
• El valor de\(B\) determina el periodo de la función sinusoidal. el periodo es igual a\(2\pi\).
• El valor de\(C\) es el desplazamiento de fase (desplazamiento horizontal) de la función sinusoidal. La gráfica se desplaza hacia la derecha si\(C > 0\) y se desplaza hacia la izquierda si\(C < 0\).
• El valor de\(D\) es el desplazamiento vertical de la sinusoide. La línea horizontal\(y = D\) es la llamada línea central para la gráfica de la función sinusoidal.
• Las notas importantes sobre sinusoides en la página 103.