3.1: Funciones trigonométricas de los ángulos

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

• ¿Cómo definimos el coseno y el seno como funciones de los ángulos?
• ¿Cómo se definen las funciones trigonométricas en ángulos usando círculos de cualquier radio?

Actividad Inicial

1. ¿Cómo definimos un ángulo cuya medida es un radián? Consulte la definición en la página 27.
2. Dibuja un ángulo en posición estándar con una medida de\(\dfrac{\pi}{4}\) radianes. Dibuja un ángulo en posición estándar con una medida de\(\dfrac{5\pi}{3}\) radianes.
3. ¿Cuál es la fórmula para la longitud del arco\(s\) en un círculo de radio\(r\) que es interceptado por un ángulo con medida de radianes\(\theta\)? Ver página 36. ¿Por qué implica esta fórmula que los radianes son una cantidad adimensional y que una medición en radianes puede considerarse como un número real?

Algunos resultados previos

En la Sección 1.2, definimos la función coseno y la función seno usando el círculo unitario. En particular, aprendimos que podíamos definir\(\cos(t)\) y\(\sin(t)\) para cualquier número real donde el número real\(t\) podría pensarse como la longitud de un arco en el círculo unitario.

En la Sección 1.3, aprendimos que la medida radianes de un ángulo es la longitud del arco en el círculo unitario que es interceptado por el ángulo. Es decir,

Un ángulo (en posición estándar) de\(t\) radianes corresponderá a un arco de longitud\(t\) en el círculo unitario, y esto nos permite pensar\(\cos(t)\) y\(\sin(t)\) cuándo\(t\) es la medida radianes de un ángulo.

Entonces, cuando pensamos en\(\cos(t)\) y\(\sin(t)\) (y las otras funciones trigonométricas), podemos considerar\(t\) que son:

• un número real;
• la longitud de un arco con punto inicial\((1, 0)\) en el círculo unitario;
• la medida radianes de un ángulo en posición estándar.

La figura\(\PageIndex{1}\) muestra un arco en el círculo unitario con el ángulo correspondiente.

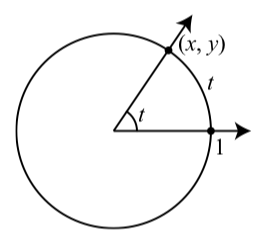
Figura\(\PageIndex{1}\): Un ángulo en posición estándar con el círculo unitario

Funciones trigonométricas de un ángulo

Con la notación en la Figura 3.1, vemos que\(\cos(t) = x\) y\(\sin(t) = y\). En este contexto, muchas veces las funciones coseno y seno circulares porque están definidas por puntos en el círculo unitario. Ahora queremos enfocarnos en la perspectiva el coseno y el seno como funciones de ángulos. Al usar esta perspectiva nos referiremos al coseno y al seno como funciones trigonométricas. Técnicamente, tenemos dos tipos diferentes de cosenos y senos: uno definido como funciones de arcos y otro como funciones de ángulos. Sin embargo, la conexión es tan cercana y la distinción tan menor que a menudo intercambiaremos los términos circular y trigonométrico. Un ítem notacional es que cuando pensamos en las funciones trigonométricas como funciones de ángulos, a menudo usamos letras griegas para los ángulos. Los más comunes son\(\theta\) (theta),\(\alpha\) (alfa),\(\beta\) (beta) y\(\phi\) (phi).

Si bien la definición de las funciones trigonométricas utiliza el círculo unitario, será bastante útil ampliar esta idea para permitirnos determinar el coseno y el seno de los ángulos relacionados con círculos de cualquier radio. El concepto principal que usaremos para hacer esto serán triángulos similares. Utilizaremos los triángulos mostrados en la Figura 3.2.

En esta figura, el ángulo\(\theta\) está en posición estándar, el punto\(P(u, v)\) está en el círculo unitario y el punto\(Q\) está en un círculo de radio\(r\). Entonces vemos eso\[\cos(\theta) = u\] y\[\sin(\theta) = v\]

Ahora usaremos los triángulos\(\triangle PAO\) y\(\triangle PAO\) para escribir\(\cos(\theta)\) y\(\sin(\theta)\) términos de\(x, y\), y\(r\). La Figura 3.3 muestra estos triángulos por sí mismos sin los círculos.

Los dos triángulos de la Figura 3.2 son triángulos similares ya que los ángulos correspondientes de los dos triángulos son iguales. (Ver página 421 en el Apéndice C.) Debido a esto, podemos escribir\[\dfrac{u}{1} = \dfrac{x}{r}\]\[u = \dfrac{x}{r}\]\[\cos(\theta) = \dfrac{x}{r}\] y\[\dfrac{u}{1} = \dfrac{y}{r}\]\[v = \dfrac{y}{r}\]\[\sin(\theta) = \dfrac{y}{r}\]

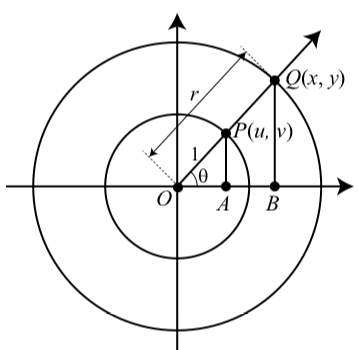
Figura\(\PageIndex{2}\): Un ángulo en posición estándar

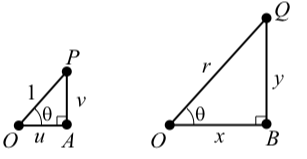
Figura\(\PageIndex{3}\): Triángulos similares a partir de la figura\(\PageIndex{2}\)

Además, tenga en cuenta que\(u^{2} + v^{2} = 1\) y\(x^{2} + y^{2} = r^{2}\). Por lo que hemos obtenido los siguientes resultados, que muestran que una vez que conocemos las coordenadas de un punto en el lado terminal de un ángulo\(\theta\) en posición estándar, podemos determinar las seis funciones trigonométricas de ese ángulo.

Para\((x, y)\) cualquier punto que no sea el origen en el lado terminal de un ángulo\(\theta\) en posición estándar, las funciones trigonométricas de se\(\theta\) definen como:\[\cos(\theta) = \dfrac{x}{r}\]\[\sin(\theta) = \dfrac{y}{r}\]\[\tan(\theta) = \dfrac{y}{x}, x \neq 0\]\[\sec(\theta) = \dfrac{r}{x}, x \neq 0\]\[\csc(\theta) = \dfrac{r}{y}, y \neq 0\]\[\cot(\theta) = \dfrac{x}{y}, y \neq 0\] dónde\(r^{2} = x^{2} + y^{2}\)\(r > 0\) y así\(r = \sqrt{x^{2}+y^{2}}\).
Observe que las otras funciones trigonométricas también se pueden determinar en términos de\(x, y\), y\(r\). Por ejemplo, si\(x \neq 0\), entonces\[\tan(\theta) = \dfrac{\sin(\theta)}{\cos(\theta)} = \dfrac{\dfrac{y}{r}}{\dfrac{x}{r}} = \dfrac{y}{r}\cdot \dfrac{r}{x} = \dfrac{y}{x}\]\[\sec(\theta) = \dfrac{1}{\cos(\theta)} = \dfrac{1}{\dfrac{x}{r}} = 1 \cdot \dfrac{r}{x} = \dfrac{r}{x}\]

Por ejemplo, si el punto\((3, -1)\) está en el lado terminal del ángulo\(\theta\), entonces podemos usar\(x = 3\),\(y = -1\), y\(r = \sqrt{(-3)^{2}+1^{2}} = \sqrt{10}\), y así

\[\cos(\theta) = \dfrac{3}{\sqrt{10}}\]\[\sin(\theta) = -\dfrac{1}{\sqrt{10}}\]\[\tan(\theta) = -\dfrac{1}{3}\]\[\cot(\theta) = -\dfrac{3}{1}\]\[\sec(\theta) = \dfrac{\sqrt{10}}{3}\]\[\csc(\theta) = -\dfrac{\sqrt{10}}{1}\]

Los dos siguientes ejercicios proporcionarán cierta práctica con el uso de estos resultados.

Ejercicio\(\PageIndex{1}\)

Supongamos que sabemos que el punto\(P(3, 7)\) está en el lado terminal del ángulo\(\theta\) en posición estándar.

1. Dibuja un sistema de coordenadas, traza el punto\(P\) y dibuja el lado terminal del ángulo\(\theta\).
2. Determinar el radio r del círculo centrado en el origen que pasa por el punto\(P(-5, 13)\). Pista:\(x^{2} + y^{2} = r^{2}\).
3. Ahora determinar los valores de las seis funciones trigonométricas de\(\theta\).

Contestar

1.

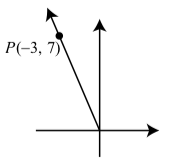
2. \(r = \sqrt{(-3)^{2} + 7^{2}} = \sqrt{58}\)

3. \[\cos(\theta) = -\dfrac{3}{\sqrt{58}}\]

\[\sin(\theta) = \dfrac{7}{\sqrt{58}}\]

\[\tan(\theta) = -\dfrac{7}{3}\]

\[\cos(\theta) = -\dfrac{3}{7}\]

\[\sec(\theta) = -\dfrac{\sqrt{58}}{3}\]

\[\tan(\theta) = \dfrac{\sqrt{58}}{7}\]

Ejercicio\(\PageIndex{2}\)

Supongamos que\(\alpha\) es un ángulo\(\tan(\alpha) = \dfrac{2}{3}\), eso, y cuando\(\alpha\) está en posición estándar, su lado terminal está en el tercer cuadrante.

1. Dibuje un sistema de coordenadas, dibuje el lado terminal del ángulo\(\alpha\) en posición estándar.
2. Determinar un punto que se encuentra en el lado terminal de\(\alpha\).
3. Determinar las seis funciones trigonométricas de\(\alpha\).

Contestar

1.

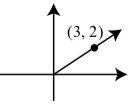
2. Ya que\(\tan(\alpha) = \dfrac{2}{3}\), podemos concluir que el punto\((3, 2)\) se encuentra en el lado terminal de\(\alpha\).

3. Ya que\((3, 2)\) está en el lado terminal de\(\alpha\) podemos usar\(x = 3, y = 2\), y\(r = \sqrt{3^{2} + 2^{2}}\). Entonces

\[\cos(\theta) = \dfrac{2}{\sqrt{13}}\]

\[\sin(\theta) = \dfrac{3}{\sqrt{13}}\]

\[\tan(\theta) = \dfrac{2}{3}\]

\[\cos(\theta) = \dfrac{3}{2}\]

\[\sec(\theta) = -\dfrac{\sqrt{13}}{2}\]

\[\tan(\theta) = \dfrac{\sqrt{13}}{3}\]

La identidad pitagórica

Quizás la identidad más importante para las funciones circulares es la llamada Identidad Pitagórica, que establece que para cualquier número real\(t\),\[\cos^{2}(t) + \sin^{2}(t) = 1\]

No debe sorprender que esta identidad también se mantenga para las funciones trigonométricas cuando consideramos que estas son funciones de ángulos. Esto se verificará en la próxima comprobación de progreso.

Ejercicio\(\PageIndex{3}\)

Dejar\(\theta\) ser un ángulo y asumir que\((x, y)\) es un punto en el lado terminal de\(\theta\) en posición estándar. Entonces dejamos\(r^{2} = x^{2} + y^{2}\). Entonces vemos que\[\cos(\theta)^{2} + \cos(\theta)^{2} = (\dfrac{x}{r})^{2} + (\dfrac{y}{r})^{2}.\]

1. Usa álgebra para reescribir\((\dfrac{x}{r})^{2} + (\dfrac{y}{r})^{2}\) como una sola fracción con denominador su lado terminal está en el tercer cuadrante.
2. Ahora usa el hecho de que\(x^{2} + y^{2} = r^{2}\) para probar que\((\dfrac{x}{r})^{2} + (\dfrac{y}{r})^{2} = 1\)
3. Por último, concluir que\[\cos(\theta)^{2} + \sin(\theta)^{2} = 1\]

Contestar

El trabajo terminado debe verse algo así como lo siguiente:

\[\cos^{2}(\theta) + \sin^{2}(\theta) = (\dfrac{x}{r})^{2} + (\dfrac{y}{r})^{2} = \dfrac{x^{2}}{r^{2}} + \dfrac{y^{2}}{r^{2}} = \dfrac{x^{2} + y^{2}}{r^{2}} = \dfrac{r^{2}}{r^{2}} = 1\]

La siguiente comprobación de progreso muestra cómo utilizar la Identidad Pitagórica para ayudar a determinar las funciones trigonométricas de un ángulo.

Ejercicio\(\PageIndex{4}\)

Supongamos que\(\theta\) es un ángulo en posición estándar y eso\(\sin(\theta) = \dfrac{1}{3}\) y\(\dfrac{\pi}{2} < \theta < \pi\).

1. Utilizar la Identidad Pitagórica para determinar\(\cos^{2}(\theta)\) y luego usar el hecho de que\(\dfrac{\pi}{2} < \theta < \pi\) para determinar\(\cos(\theta)\).
2. Utilice la identidad\(\tan(\theta) = \dfrac{\sin(\theta)}{\cos(\theta)}\) para determinar el valor de\(\tan(\theta)\).
3. Determinar los valores de las otras tres funciones trigonométricas de\(\theta\).

Contestar

1. Usando la Identidad Pitagórica, vemos eso\(\cos^{2}(\theta) + (\dfrac{1}{3})^{2} = 1\) y así\(\cos^{2}(\theta) = \dfrac{8}{9}\). Ya que\(\dfrac{\pi}{2} < \theta < \pi\),\(\cos(\theta) < 0\). De ahí,\(\cos(\theta) = -\dfrac{\sqrt{8}}{3}\).

2. \(\tan(\theta) = \dfrac{\dfrac{1}{3}}{-\dfrac{\sqrt{8}}{3}} = -\dfrac{1}{\sqrt{8}}\).

3. \(\cot(\theta) = -\sqrt{8}, \csc(\theta) = 3\), y\(\sec(\theta) = -\dfrac{3}{\sqrt{8}}\)

Las funciones trigonométricas inversas

En la Sección 2.5, estudiamos las funciones trigonométricas inversas cuando consideramos que las funciones trigonométricas (circulares) son funciones de un número real\(t\). Al inicio de esta sección, sin embargo, vimos que también\(t\) podría considerarse como la longitud de un arco en el círculo unitario, o la medida radianes de un ángulo en posición estándar. En ese momento, estábamos usando el círculo unitario para determinar la medida radianes de un ángulo pero ahora podemos usar cualquier punto en el lado terminal del ángulo para determinar el ángulo. Lo importante es que estas son ahora funciones de ángulos y así podemos usar las funciones trigonométricas inversas para determinar ángulos. Podemos usar medida de radianes o medida de grado para los ángulos. Los resultados que necesitamos se resumen a continuación.

1. \(\theta = \arcsin(x) = \sin^{-1}(x)\)medios\(\sin(\theta) = x\) y\(-\dfrac{\pi}{2} \leq \theta \leq \dfrac{\pi}{2}\) o\(-90^\circ \leq \theta \leq 90^\circ\).
2. \(\theta = \arccos(x) = \cos^{-1}(x)\)medios\(\cos(\theta) = x\) y\(0 \leq \theta \leq \pi\) o\(0^\circ \leq \theta \leq 180^\circ\).
3. \(\theta = \arctan(x) = \tan^{-1}(x)\)medios\(\tan(\theta) = x\) y\(-\dfrac{\pi}{2} < \theta < \dfrac{\pi}{2}\) o\(-90^\circ < \theta < 90^\circ\).

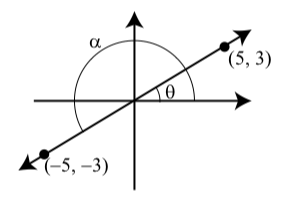
Lo importante a recordar es que una ecuación que involucra la función trigonométrica inversa puede traducirse en una ecuación que involucra la función trigonométrica correspondiente y que el ángulo debe estar en un cierto rango. Por ejemplo, si sabemos que el punto\((5, 3)\) está en el lado terminal de un ángulo\(\theta\) y eso\(0 \leq \theta < \pi\), entonces sabemos que\[\tan(\theta) = \dfrac{y}{x} = \dfrac{3}{5}\]

Podemos usar la función tangente inversa para determinar (y aproximar) el ángulo ya que la función tangente inversa da un ángulo (en medida de radianes) entre\(-\dfrac{\pi}{2}\) y\(\dfrac{\pi}{2}\). Ya que\(\tan(\theta) > 0\), obtendremos un ángulo entre 0 y\(\dfrac{\pi}{2}\). \[\theta = \arctan(\dfrac{3}{5}) \approx 0.54042\]

Si usáramos medida de grado, obtendríamos\(\dfrac{\pi}{2}\). \[\theta = \arctan(\dfrac{3}{5}) \approx 30.96376^\circ\]

Es importante señalar que al utilizar las funciones trigonométricas inversas, debemos tener cuidado con las restricciones en los ángulos. Por ejemplo, si hubiéramos dicho eso\(\tan(\alpha) = \dfrac{5}{3}\) y\(\pi < \alpha < \dfrac{3\pi}{2}\), entonces la función tangente inversa no daría el resultado correcto. Todavía podríamos usar\[\theta = \arctan(\dfrac{3}{5}) \approx 0.54042\] pero ahora tendríamos que usar este resultado y el hecho de que el lado terminal de\(\alpha\) está en el tercer cuadrante. Entonces\[\alpha = \theta + \pi\]\[\alpha = \arctan(\dfrac{3}{5}) + \pi\]\[\alpha \approx 3.68201\]

Ahora deberíamos usar una calculadora para verificar que\(\tan(\alpha) = \dfrac{3}{5}\)

La relación entre los ángulos\(\alpha\) y\(\theta\) se muestra en la Figura\(\PageIndex{4}\).

Ejercicio\(\PageIndex{1}\)

Supongamos que el punto\((-2, 5)\) está en el lado terminal del ángulo\(\theta\) en posición estándar y eso\(0 \leq \theta < 360^\circ\). Entonces lo sabemos\(\tan(\theta) = -\dfrac{5}{2} = -2.5\).

Figura\(\PageIndex{4}\): Dos ángulos con el mismo valor tangente

1. Dibuja una imagen del ángulo\(\theta\).
2. Utilice una calculadora para aproximar el valor de\(\tan^{-1}(-2.5)\) a tres decimales.
3. Observe que\(\tan^{-1}(-2.5)\) es un ángulo negativo y no puede igualar\(\theta\) ya que\(\theta\) es un ángulo positivo. Utilice la aproximación para\(\tan^{-1}(-2.5)\) para determinar una aproximación de\(\theta\) hasta tres decimales.

Contestar

2. \(\tan^{-1}(-2.5) \approx -68.199^\circ\)

3. \(\theta = -68.199^\circ + 180^\circ \approx 111.801^\circ\)

En el siguiente ejemplo, determinaremos el valor exacto de un ángulo que se da en términos de una función trigonométrica inversa.

Ejemplo\(\PageIndex{1}\): Determining an Exact Value

Determinaremos el valor exacto de\(\cos(\arcsin(-\dfrac{2}{7}))\). Observe que podemos usar una calculadora para determinar que\[\cos(\arcsin(-\dfrac{2}{7})) \approx 0.958315\]

A pesar de que esto es correcto a seis decimales, no es el valor exacto. Podemos usar esta aproximación, sin embargo, para consultar nuestro trabajo a continuación.

Nos\(\theta = \arcsin(-\dfrac{2}{7})\) lo dejamos saber entonces\[\sin(\theta) = -\dfrac{2}{7}\] y\[-\dfrac{\pi}{2} \leq \theta \leq \dfrac{\pi}{2}\]

Observamos que desde\(\sin(\theta) < 0\), en realidad sabemos eso\(-\dfrac{\pi}{2} \leq \theta \leq 0\).

Así podemos usar la Identidad Pitagórica para determinar de la\(\cos^{2}(\theta)\) siguiente manera:\[\cos^{2}(\theta) + \sin^{2}(\theta) = 1\]\[\cos^{2}(\theta) = 1 - (-\dfrac{2}{7})^{2}\]\[\cos^{2}(\theta) = \dfrac{45}{49}\]

Ya que\(-\dfrac{\pi}{2} \leq \theta \leq 0\), vemos eso\(\cos(\theta) = \dfrac{\sqrt{45}}{7}\). Eso es\[\cos(\arcsin(-\dfrac{2}{7})) = \dfrac{\sqrt{45}}{7}.\]

Ahora podemos usar una calculadora para verificar eso\(\dfrac{\sqrt{45}}{7} \approx 0.958315\).

Resumen

En esta sección, se estudiaron los siguientes conceptos e ideas importantes:

Las funciones trigonométricas se pueden definir usando cualquier punto en el lado terminal de un ángulo en posición estándar. Para\((x, y)\) cualquier punto que no sea el origen en el lado terminal de un ángulo\(\theta\) en posición estándar, las funciones trigonométricas de\(\theta\) se definen como:

\[\cos(\theta) = \dfrac{x}{r}\]\[\sin(\theta) = \dfrac{y}{r}\]\[\tan(\theta) = \dfrac{y}{x}, x \neq 0\]\[\sec(\theta) = \dfrac{r}{x}, x \neq 0\]\[\csc(\theta) = \dfrac{r}{y}, y \neq 0\]\[\cot(\theta) = \dfrac{x}{y}, y \neq 0\]dónde\(r^{2} = x^{2} + y^{2}\)\(r > 0\) y así\(r = \sqrt{x^{2}+y^{2}}\). La pitagoreanidentidad sigue siendo cierta cuando utilizamos las funciones trigonométricas de un ángulo. Es decir, para cualquier ángulo,\[\cos(\theta)^{2} + \sin(\theta)^{2} = 1.\]
además, todavía tenemos las funciones trigonométricas inversas. En particular,

• \(\theta = \arcsin(x) = \sin^{-1}(x)\)medios\(\sin(\theta) = x\) y\(-\dfrac{\pi}{2} \leq \theta \leq \dfrac{\pi}{2}\) o\(-90^\circ \leq \theta \leq 90^\circ\).
• \(\theta = \arccos(x) = \cos^{-1}(x)\)medios\(\cos(\theta) = x\) y\(0 \leq \theta \leq \pi\) o\(0^\circ \leq \theta \leq 180^\circ\).
• \(\theta = \arctan(x) = \tan^{-1}(x)\)medios\(\tan(\theta) = x\) y\(-\dfrac{\pi}{2} < \theta < \dfrac{\pi}{2}\) o\(-90^\circ < \theta < 90^\circ\).