3.2: Triángulos rectos

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

• ¿Cómo relaciona el coseno lados y ángulos agudos en un triángulo rectángulo? ¿Por qué?
• ¿Cómo relaciona el seno lados y ángulos agudos en un triángulo rectángulo? ¿Por qué?
• ¿Cómo relaciona la tangente lados y ángulos agudos en un triángulo rectángulo? ¿Por qué?
• ¿Cómo podemos usar el coseno, el seno y la tangente de un ángulo en un triángulo rectángulo para ayudar a determinar partes desconocidas de ese triángulo?

Actividad de inicio

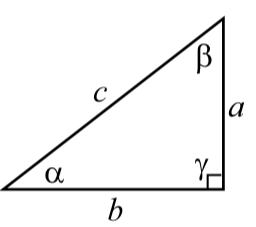
El siguiente diagrama muestra un típico triángulo rectángulo. Las longitudes de los tres lados del triángulo rectángulo se etiquetan como\(a\),\(b\), y\(c\). Los ángulos opuestos a los lados de las longitudes\(a\)\(b\),, y\(c\) están etiquetados\(\alpha\) (alfa),\(\beta\) (beta) y\(\gamma\) (gamma), respectivamente. (Alfa, beta y gamma son las tres primeras letras del alfabeto griego). El pequeño cuadrado con el ángulo\(\gamma\) indica que este es el ángulo recto en el triángulo recto. El triángulo, por supuesto, tiene tres lados. Llamamos al lado opuesto al ángulo recto (el lado de longitud\(c\) en el diagrama) la hipotenusa del triángulo rectángulo.

Cuando trabajamos con triángulos, los ángulos suelen medirse en grados y así diríamos que\(\gamma\) es un ángulo de\(90^\circ\).

1. ¿Qué podemos concluir sobre\(a\)\(b\), y\(c\) a partir del Teorema de Pitágoras? Cuando se trabaja con triángulos, generalmente medimos ángulos en grados. Para la parte fraccional de la medida de grado de un ángulo, a menudo usamos decimales pero también usamos frecuentemente minutos y segundos.
2. ¿Cuál es la suma de los ángulos en un triángulo? En este caso, ¿qué es\(\alpha + \beta + \gamma\)?
3. Cuál es la suma de los dos ángulos agudos en un triángulo rectángulo. En este caso, ¿qué es\(\alpha + \beta\)?
4. ¿Cuántos minutos hay en un grado? ¿Cuántos segundos hay en un minuto?
5. Determinar la solución de la ecuación\(7.3 = \dfrac{118.8}{x}\) correcta a la milésima más cercana. (Deberías poder demostrarlo\(x \approx 2.575\).)
6. Determinar la solución de la ecuación\((\sin^\circ) = \dfrac{5}{x}\) correcta a la diezmilésima más cercana. (Deberías poder demostrarlo\(x \approx 9.4354\).)

Supongamos que desea encontrar la altura de un objeto alto como un asta de bandera (o un árbol o un edificio). Podría ser inconveniente (o incluso peligroso) subir al asta de la bandera y medirlo, entonces, ¿qué puedes hacer? Podría ser fácil medir la longitud de la sombra que proyecta el asta de la bandera y también el ángulo\(\theta\) determinado por el nivel del suelo al sol (llamado ángulo de elevación del objeto) como en la Figura\(\PageIndex{1}\). En esta sección aprenderemos a usar las funciones trigonométricas para relacionar longitudes de lados con ángulos en triángulos rectos y resolver este problema así como muchos otros.

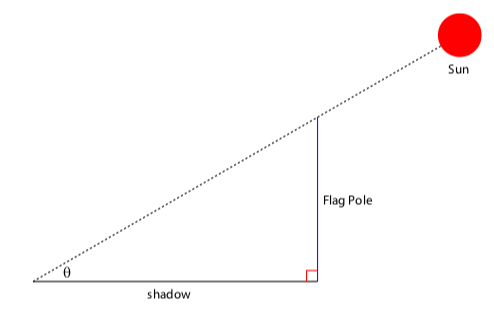
Figura\(\PageIndex{1}\): Encontrar la altura de un asta de bandera (dibujo no a escala)

Funciones trigonométricas y triángulos rectos

Hemos visto cómo determinamos los valores de las funciones trigonométricas de un ángulo\(\theta\) colocando\(\theta\) en posición estándar y dejando\((x, y)\) ser el punto de intersección del lado terminal del ángulo\(\theta\) con un círculo de radio\(r\). Entonces

1. \(\cos(\theta) = \dfrac{x}{r}\)
2. \(\sin(\theta) = \dfrac{y}{r}\)
3. \(\tan(\theta) = \dfrac{y}{x}\)si\(x \neq 0\)
4. \(\sec(\theta) = \dfrac{r}{x}\)si\(x \neq 0\)
5. \(\csc(\theta) = \dfrac{r}{y}\)si\(y \neq 0\)
6. \(\cot(\theta) = \dfrac{x}{y}\)si\(y \neq 0\)

En nuestro trabajo con triángulos rectos, utilizaremos únicamente las funciones seno, coseno y tangente.

Ahora veremos cómo relacionar las funciones trigonométricas con ángulos en triángulos rectos. Supongamos que tenemos un triángulo rectángulo con lados de longitud\(x\) y\(y\) e hipotenusa de longitud\(r\). Dejar\(\theta\) ser el ángulo opuesto al lado de longitud\(y\) como se muestra en la Figura\(\PageIndex{2}\). Ahora podemos colocar nuestro triángulo de tal manera que el ángulo\(\theta\) esté en posición estándar en el plano y el triángulo encaje en el círculo de radio\(r\) como se muestra a la derecha en la Figura\(\PageIndex{3}\).

Por la definición de nuestras funciones trigonométricas tenemos entonces

\[\cos(\theta) = \dfrac{x}{r}\]

\[\sin(\theta) = \dfrac{y}{r}\]

\[\tan(\theta) = \dfrac{y}{x}\]

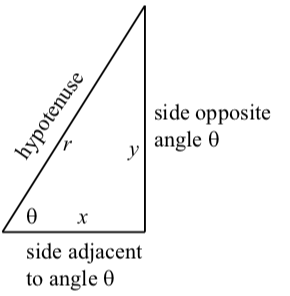
Si en lugar de usar\(x\)\(y\),\(r\), y, etiquetamos\(y\) como la longitud del lado opuesto al ángulo agudo\(\theta\),\(x\) como la longitud del lado adyacente al ángulo agudo\(\theta\), y\(r\) como la longitud de la hipotenusa, obtenemos la siguiente figura:

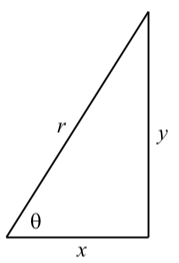
Figura\(\PageIndex{2}\): Un triángulo rectángulo

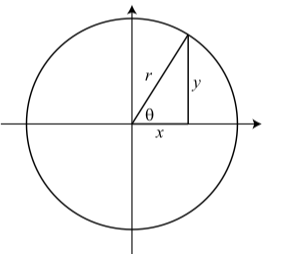
Figura\(\PageIndex{3}\): Triángulo recto en posición estándar

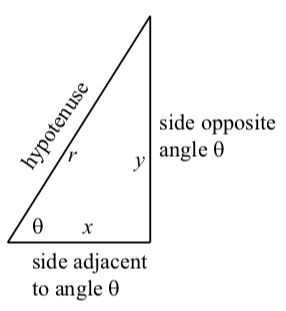
Entonces vemos que

\[\sin(\theta) = \dfrac{length \space of \space side \space opposite\space \theta}{length \space of \space hypotenuse} \space\space \sin(\theta) = \dfrac{opposite}{hypotenuse}\]

\[\cos(\theta) = \dfrac{length \space of \space side \space adjacent\space to \space \theta}{length \space of \space hypotenuse} \space\space \cos(\theta) = \dfrac{adjacent}{hypotenuse}\]

\[\tan(\theta) = \dfrac{length \space of \space side \space opposite\space \theta}{length \space of \space side \space adjacent\space to \space \theta} \space\space \tan(\theta) = \dfrac{opposite}{adjacent}\]

Las ecuaciones de la derecha son abreviaturas convenientes de las ecuaciones correctas a la izquierda.

Ejercicio\(\PageIndex{1}\)

Debemos tener cuidado cuando usamos los términos opuestos y adyacentes porque el significado de estos términos depende del ángulo que estemos usando. Utilice los diagramas de la Figura 3.8 para determinar fórmulas para cada una de las siguientes en términos de a, b y c.

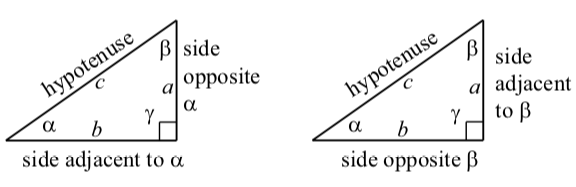
Figura\(\PageIndex{4}\): Etiquetas para un triángulo rectángulo

1. \(\cos(\alpha) = ?\)
2. \(\sin(\alpha) = ?\)
3. \(\tan(\alpha) = ?\)
4. \(\cos(\beta) = ?\)
5. \(\sin(\beta) = ?\)
6. \(\tan(\beta) = ?\)

También hay que señalar que con el etiquetado del triángulo rectángulo que se muestra en la Figura\(\PageIndex{4}\), podemos utilizar el Teorema de Pitágoras y el hecho de que la suma de los ángulos de un triángulo es\(180\) grados para concluir que\[a^{2} + b^{2} = c^{2}\] y\[\alpha + \beta + \gamma = 180^\circ\]\[\gamma = 90^\circ\]\[\alpha + \beta = 90^\circ\]

Ejemplo\(\PageIndex{1}\)

Supongamos que uno de los ángulos agudos de un triángulo rectángulo tiene una medida de\(35^\circ\) y que el lado adyacente a este ángulo es de 8 pulgadas de largo. Determinar el otro ángulo agudo del triángulo rectángulo y las longitudes de los otros dos lados.

Solución

Lo primero que hacemos es dibujar una imagen del triángulo. (La imagen no tiene que ser perfecta pero debería reflejar razonablemente la información dada). Al hacer el diagrama, también debemos etiquetar las partes desconocidas del triángulo. Una forma de hacerlo se muestra en el diagrama.

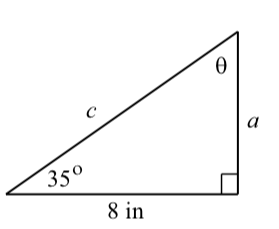
Una cosa que notamos es que\(35^\circ + \theta = 90^\circ\) y\(\theta = 55^\circ\). También podemos usar el coseno y la tangente de\(35^\circ\) para determinar los valores de\(a\) y\(c\).

\[ \begin{align*} \cos(35^\circ) &= \dfrac{8}{c} \\[4pt] c\cos(35^\circ) &= 8 \\[4pt] c &= \dfrac{8}{\cos(35^\circ)} \\[4pt] c &\approx 9.76620 \end{align*}\]

\[ \begin{align*} \tan(35^\circ) &= \dfrac{a}{8} \\[4pt] 8\tan(35^\circ) &= a \\[4pt] a &\approx 5.60166 \end{align*}\]

Antes de decir que este ejemplo está completo, debemos verificar nuestros resultados. Una forma de hacerlo es verificar que las longitudes de los tres lados del triángulo rectángulo satisfacen la fórmula para el Teorema de Pitágoras. Usando el valor dado para un lado y los valores calculados de\(a\) y\(c\), vemos que

\[8^{2} + a^{2} \approx 95.379\]\[c^{2} \approx 95.379 \nonumber\]

Entonces vemos que nuestro trabajo comprueba con el Teorema de Pitágoras.

Resolviendo triángulos rectos

Lo que hicimos en Ejemplo\(\PageIndex{1}\) es lo que se llama resolver un triángulo rectángulo. Tenga en cuenta que esta frase es engañosa porque realmente no se puede “resolver” un triángulo. Desafortunadamente, esta frase está encajada en la lengua vernácula de la trigonometría y así seguiremos utilizándola. La idea es que si se nos da suficiente información sobre las longitudes de los lados y las medidas de los ángulos en un triángulo rectángulo, entonces podemos determinar todos los demás valores. El siguiente chequeo de progreso es también un ejemplo de “resolver un triángulo rectángulo”.

Ejercicio\(\PageIndex{2}\)

La longitud de la hipotenusa de un triángulo rectángulo es\(17\) pies y la longitud de un lado de este triángulo rectángulo es\(5\) pies. Determinar la longitud del otro lado y los dos ángulos agudos para este triángulo rectángulo.

Pista: Dibuje una imagen y etiquete el tercer lado del triángulo rectángulo con una variable y etiquete los dos ángulos agudos como\(\alpha\) y\(\beta\).

Contestar

Dejamos\(\alpha\) ser el ángulo opuesto al lado de longitud\(5\) pies y dejamos\(\beta\) ser el ángulo adyacente a ese lado. Entonces vemos que

\[\sin(\alpha) = \dfrac{5}{17}\]\[\alpha = \arcsin(\dfrac{5}{17})\]\[\alpha \approx 17.1046^\circ\]

\[\cos(\beta) = \dfrac{5}{17}\]\[\beta = \arccos(\dfrac{5}{17})\]\[\beta \approx 72.8954^\circ\]

Como cheque, lo notamos\(\alpha + \beta = 90^\circ\). Podemos usar el teorema de Pitágoras para determinar el tercer lado, que usando nuestra notación, es\(b\). Entonces\[5^{2} + b^{2} = 17^{2}\]

y así vemos que\(b = \sqrt{264} \approx 16.2481\) los pies.

Aplicaciones de Triángulos Retos

Como los ejemplos han ilustrado hasta este punto, al trabajar en problemas que involucran triángulos rectos (incluyendo problemas de aplicación), debemos:

• Dibuja un diagrama para el problema.
• Identifica las cosas que sabes sobre la situación. En su caso, incluya esta información en su imagen.
• Identificar la cantidad que hay que determinar y dar a esta cantidad un nombre de variable. En su caso, incluya esta información en su diagrama.
• Encontrar una ecuación que relacione lo que se sabe con lo que se debe determinar. Esto a menudo implicará una función trigonométrica o el Teorema de Pitágoras.
• Resuelve la ecuación para lo desconocido. Entonces piensa en esta solución para asegurarte de que tenga sentido en el contexto del problema.
• Si es posible, encuentra la manera de verificar el resultado.

Volvemos al ejemplo dado en la introducción a esta sección de la página 179. En este ejemplo, se utilizó el término ángulo de elevación. Este es un término común (así como ángulo de depresión) en problemas que involucran triángulos. Podemos definir un ángulo de elevación de un objeto para que sea un ángulo cuyo lado inicial sea horizontal y tenga una rotación para que el lado terminal esté por encima de la horizontal. Un ángulo de depresión es entonces un ángulo cuyo lado inicial es horizontal y tiene una rotación para que el lado terminal esté por debajo de la horizontal (Figura 3.9).

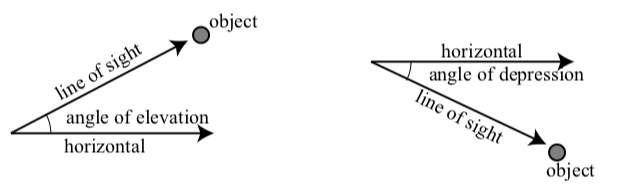
Figura\(\PageIndex{5}\): Ángulo de elevación y ángulo de depresión

Ejemplo\(\PageIndex{2}\): Determining the Height of a Flagpole

Supongamos que queremos determinar la altura de un asta de bandera y no podemos medir la altura directamente. Supongamos que medimos la longitud de la sombra del asta de la bandera para ser\(44\) pies,\(5\) pulgadas. Además, medimos el ángulo de elevación del sol a ser\(33^\circ15'\).

Contestar

Lo primero que hacemos es dibujar el diagrama. En el diagrama, dejamos\(h\)

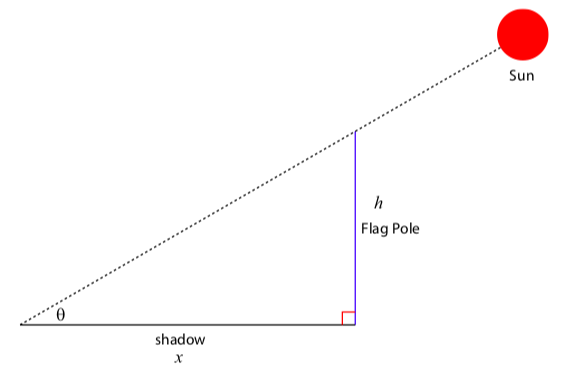
Figura\(\PageIndex{6}\): Encontrar la altura de un asta de bandera (dibujo no a escala)

ser la altura del asta de la bandera,\(x\) ser la longitud de la sombra, y\(\theta\) ser el ángulo de elevación. Se nos dan valores para\(x\) y\(\theta\), y vemos que

\[\tan(\theta) = \dfrac{h}{x}\]\[x\tan(\theta) = h\]

Entonces ahora podemos determinar el valor de\(h\), pero debemos tener cuidado de usar un valor decimal (o fraccionario) para\(x\) (equivalente a 44 pies, 5 pulgadas) y un valor decimal (o fraccionario) para\(\theta\) (equivalente a\(33^\circ15'\)). Entonces usaremos\[x = 44 + \dfrac{5}{12}\] y\[\theta = (33 + \dfrac{15}{60})^\circ\]

Usando esto y la ecuación (1), vemos que\[h = (44 + \dfrac{5}{12})\tan(33 + \dfrac{15}{60})^\circ\]\[h \approx 29.1208 \space feet\]

La altura del asta de la bandera es de unos\(29.12\) pies o\(29\) pies,\(1.4\) pulgadas.

Ejercicio\(\PageIndex{3}\)

Una empresa necesita construir una rampa accesible para sillas de ruedas a su entrada. Los Lineamientos de la Ley de Estadounidenses con Discapacidades para Edificios e Instalaciones para rampas establecen que “La pendiente máxima de una rampa en nueva construcción será”\(1:12\).

1. La\(1:12\) pauta significa que por cada 1 pie de subida en la rampa debe haber\(12\) pies de carrera. ¿Cuál es el ángulo de elevación (en grados) de tal rampa?
2. Si la entrada de la compañía está a\(7.5\) pies sobre el suelo nivelado, utilice la trigonometría para aproximar la longitud de la rampa que la compañía necesitará construir utilizando la pendiente máxima. Explica tu proceso.

Contestar

Con un ascenso de\(1\) pie por cada\(12\) pie de carrera, vemos si dejamos\(\theta\) ser el ángulo de elevación, entonces

\[\tan(\theta) = \dfrac{1}{12}\]

\[\theta = \arctan(\dfrac{1}{12})\]

\[\theta \approx 4.7636^\circ\]

La longitud de la rampa será la hipotenusa del triángulo rectángulo. Entonces si dejamos\(h\) ser la longitud de la hipotenusa, entonces

\[\sin(\theta) = \dfrac{7.5}{h}\]

\[h = \dfrac{7.5}{\sin(\theta)}\]

\[h \approx 90.3120\]

La longitud de la hipotenusa es de aproximadamente\(90.3\) pies. Podemos verificar nuestro resultado determinando la longitud del tercer lado, que es\(7.5 \cdot 12\) o\(90\) pies y luego verificando el resultado del teorema de Pitágoras. Podemos verificar que

\[7.5^{2} + 90^{2} \approx 90.3120^{2}.\]

Ejercicio\(\PageIndex{4}\)

Esta es una variación del Ejemplo 3.19. Supongamos que el asta se asienta en lo alto de un cerro y que no podemos medir directamente la longitud de la sombra del asta como se muestra en la Figura 3.19.

Algunas cantidades han sido etiquetadas en el diagrama. Ángulos\(\alpha\) y\(\beta\) son ángulos de elevación a la parte superior del asta de la bandera desde dos puntos diferentes en terreno llano. Estos puntos están a\(d\) pies de distancia y directamente en línea con el asta de la bandera. El problema

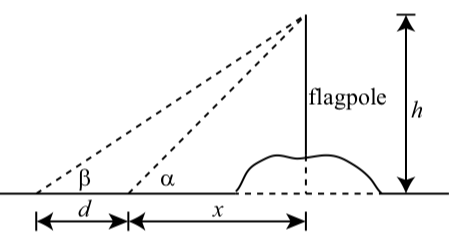
Figura\(\PageIndex{7}\): Asta de bandera en una colina

es determinar\(h\), la altura desde el suelo nivelado hasta la parte superior del asta de la bandera. Se han registrado las siguientes mediciones.

\[\alpha = 43.2^\circ\]\[\beta = 34.7^\circ\]\[d = 22.75 feet\]

Observe que no\(x\) se dio un valor para porque es la distancia desde el primer punto hasta un punto imaginario directamente debajo del asta de la bandera e incluso con terreno nivelado.

Por favor, tenga en cuenta que probablemente sea más fácil escribir fórmulas en términos de\(\alpha\),\(\beta\),\(\gamma\) y esperar hasta el final para usar los valores numéricos. Por ejemplo, vemos eso\[\tan(\alpha) = \dfrac{h}{x}\] y\[\tan(\beta) = \dfrac{h}{d + x}\]

En la ecuación (1), observe que conocemos el valor de\(\alpha\). Esto significa que si podemos determinar un valor para cualquiera\(x\) o\(h\), podemos usar la ecuación (1) para determinar el valor del otro. Primero determinaremos el valor de\(x\).

1. Resolver la ecuación (1) para h y luego sustituirla por la ecuación (2). Llama a esta ecuación (3).
2. Uno de los términos de la ecuación (3) tiene un denominador. Multiplique ambos lados de la ecuación (3) por este denominador.
3. Ahora resuelve la ecuación resultante para\(x\) (en términos de\(\alpha\),\(\beta\), y\(\gamma\)).
4. Sustituir los valores dados por\(\alpha\)\(\beta\),, y\(\gamma\) para determinar el valor de\(x\) y

   luego use este valor y la ecuación (1) para determinar el valor de\(h\).

5. ¿Hay alguna manera de verificar para asegurarse de que el resultado es correcto?

Contestar

1. \(h = x\tan(\alpha)\). Entonces\[\tan(\beta) = \dfrac{x\tan(\alpha)}{d + x}\]

2. \(\tan(\beta)(d + x) = x\tan(\alpha)\)

3. Podemos proceder a resolver para x de la siguiente manera:

\[d\tan(\beta) + x\tan(\beta) = x\tan(\alpha)\]

\[d\tan(\beta) = x\tan(\alpha) - x\tan(\beta)\]

\[d\tan(\beta) = x(\tan(\alpha) - \tan(\beta))\]

\[\dfrac{d\tan(\beta)}{\tan(\alpha) - \tan(\beta)} = x\]

Entonces vemos eso\(x = \dfrac{22.75\tan(34.7^\circ)}{\tan(43.2^\circ) - \tan(34.7^\circ)} \approx 63.872\). Usando este valor\(x\) obtenemos\(h = x\tan(43.2^\circ) \approx 59.980\). Entonces la parte superior del asta de la bandera está a unos\(59.98\) pies sobre el suelo.

4. Hay varias formas de verificar este resultado. Una es usar los valores para\(d, h\), y\(x\) y la función tangente inversa para determinar los valores para\(\alpha\) y\(\beta\). Si utilizamos valores aproximados para\(d, h\), y\(x\), estas comprobaciones pueden no ser exactas. Por ejemplo,

\[\alpha = \arctan(\dfrac{h}{x}) \approx \arctan(\dfrac{59.98}{63.872}) \approx 43.2^\circ\]

\[\beta = \arctan(\dfrac{h}{d + x}) \approx \arctan(\dfrac{59.980}{22.75 + 63.872}) \approx 34.7^\circ\]

Otro método para verificar los resultados es usar el seno de\(\alpha\) o\(\beta\) determinar la longitud de la hipotenusa de uno de los triángulos rectos y luego verificar usando el Teorema de Pitágoras.

Resumen

En esta sección, estudiamos los siguientes conceptos e ideas importantes:

Dada suficiente información sobre las longitudes de los lados y las medidas de los ángulos en un triángulo rectángulo, podemos determinar todos los demás valores usando las siguientes relaciones:

\[\sin(\theta) = \dfrac{opposite}{hypotenuse}\]

\[\cos(\theta) = \dfrac{adjacent}{hypotenuse}\]

\[\tan(\theta) = \dfrac{opposite}{adjacent}\]