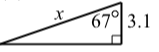3.E: Triángulos y Vectores (Ejercicios)

Ejercicio\(\PageIndex{1}\)

En cada una de las siguientes, se dan las coordenadas de un punto\(P\) en el lado terminal de un ángulo\(\theta\). Para cada una de las siguientes:

Trazar el punto\(P\) en un sistema de coordenadas y dibujar el lado terminal del ángulo.

Determinar el radio\(r\) del círculo centrado en el origen que pasa por el punto\(P\).

Determinar los valores de las seis funciones trigonométricas del ángulo\(\theta\).

1. \(P(3, 3)\)
2. \(P(5, 8)\)
3. \(P(-2, -2)\)
4. \(P(5, -2)\)
5. \(P(-1, -4)\)
6. \(P(2\sqrt{3}, 2)\)
7. \(P(-3, 4)\)
8. \(P(3, -3\sqrt{3})\)
9. \(P(2, -1)\)

Contestar

(a) Eso lo vemos\(r = \sqrt{3^{2} + 3^{2}} = \sqrt{18}\). Entonces

\[\cos(\theta) = \dfrac{3}{\sqrt{18}} = \dfrac{3}{3\sqrt{2}} = \dfrac{1}{\sqrt{2}}\]

\[\tan(\theta) = \dfrac{3}{3} = 1\]

\[\sec(\theta) = \dfrac{\sqrt{18}}{3} = \sqrt{2}\]

\[\sin(\theta) = \dfrac{3}{\sqrt{18}} = \dfrac{3}{3\sqrt{2}} = \dfrac{1}{\sqrt{2}}\]

\[\cot(\theta) = \dfrac{3}{3} = 1\]

\[\csc(\theta) = \dfrac{\sqrt{18}}{3} = \sqrt{2}\]

b)

Eso lo vemos\(r = \sqrt{5^{2} + 8^{2}} = \sqrt{89}\). Entonces

\[\cos(\theta) = \dfrac{5}{\sqrt{89}}\]

\[\tan(\theta) = \dfrac{8}{5}\]

\[\sec(\theta) = \dfrac{\sqrt{89}}{5}\]

\[\sin(\theta) = \dfrac{8}{\sqrt{89}}\]

\[\cot(\theta) = \dfrac{5}{8} = 1\]

\[\csc(\theta) = \dfrac{\sqrt{89}}{8}\]

(e)

Eso lo vemos\(r = \sqrt{(-1)^{2} + (-4)^{2}} = \sqrt{26}\). Entonces

\[\cos(\theta) = \dfrac{-3}{\sqrt{26}}\]

\[\tan(\theta) = 4\]

\[\sec(\theta) = -\dfrac{\sqrt{26}}{4}\]

\[\sin(\theta) = \dfrac{-3}{\sqrt{26}}\]

\[\cot(\theta) = \dfrac{1}{4} = 1\]

\[\csc(\theta) = -\sqrt{26}\]

Ejercicio\(\PageIndex{2}\)

Para cada una de las siguientes, dibuje el lado terminal del ángulo indicado en un sistema de coordenadas y determine los valores de las seis funciones trigonométricas de ese ángulo

1. El lado terminal del ángulo\(\alpha\) está en el primer cuadrante y\(\sin(\alpha) = \dfrac{1}{\sqrt{3}}\)
2. El lado terminal del ángulo\(\beta\) está en el segundo cuadrante y\(\cos(\beta) = -\dfrac{2}{3}\)
3. El lado terminal del ángulo\(\gamma\) está en el segundo cuadrante y\(\tan(\gamma) = -\dfrac{1}{2}\)
4. El lado terminal del ángulo\(\theta\) está en el segundo cuadrante y\(\sin(\theta) = \dfrac{1}{3}\)

Contestar

2. Primero usamos la Identidad Pitagórica y obtenemos\(\sin^{2}(\beta) = \dfrac{5}{9}\). Dado que el lado terminal de\(\beta\) está en el segundo cuadrante,\(\sin(\beta) = \dfrac{\sqrt{5}}{3}\). Además,

\[\tan(\beta) = -\dfrac{\sqrt{5}}{2}\]

\[\cot(\beta) = -\dfrac{2}{\sqrt{5}}\]

\[\sec(\beta) = -\dfrac{3}{2}\]

\[\csc(\beta) = \dfrac{3}{\sqrt{5}}\]

Ejercicio\(\PageIndex{3}\)

Para cada una de las siguientes, determinar una aproximación para el ángulo\(\theta\) en grados (a tres decimales) cuando\(0^\circ \leq \theta \leq 360^\circ\).

1. El punto\((3, 5)\) está en el lado terminal de\(\theta\).
2. El punto\((2, -4)\) está en el lado terminal de\(\theta\).
3. \(\sin(\theta) = \dfrac{2}{3}\)y el lado terminal de\(\theta\) está en el segundo cuadrante.
4. \(\sin(\theta) = -\dfrac{2}{3}\)y el lado terminal de\(\theta\) está en el cuarto cuadrante.
5. \(\cos(\theta) = -\dfrac{1}{4}\)y el lado terminal de\(\theta\) está en el segundo cuadrante.
6. \(\cos(\theta) = -\dfrac{3}{4}\)y el lado terminal de\(\theta\) está en el tercer cuadrante.

Contestar

3. Dado que el lado terminal de\(\theta\) está en el segundo cuadrante, no\(\theta\) es el seno inverso de\(\dfrac{2}{3}\). Así que dejamos\(\alpha = \arcsin(\dfrac{2}{3})\). Usando\(\alpha\) como ángulo de referencia, entonces vemos que\[\theta = 180^\circ - \arcsin(\dfrac{2}{3}) \approx 138.190^\circ\]

5. \(\theta = \arccos(-\dfrac{1}{4}) \approx 104.478^\circ\), o use\ (\ alpha\ =\ arccos (\ dfrac {1} {4})) para el ángulo de referencia.

\[\theta = 180^\circ - \arccos(\dfrac{1}{4}) \approx 104.478^\circ.\]

Ejercicio\(\PageIndex{4}\)

Para cada uno de los ángulos en el Ejercicio (3), determinar la medida radián de\(\theta\) if\(0 \leq \theta \leq 2\pi\).

Contestar

3. \(\theta = \pi - \arcsin(\dfrac{2}{3}) \approx 2.142.\)

5. \(\theta = \pi - \arccos(\dfrac{1}{4}) \approx 1.823.\)

Ejercicio\(\PageIndex{5}\)

Determinar el valor exacto de cada uno de los siguientes. Consulta todos los resultados con una calculadora.

1. \(\cos(\arcsin(\dfrac{1}{5}))\)
2. \(\tan(\cos^{-1}(\dfrac{2}{3}))\)
3. \(\sin(\tan^{-1}(2))\)
4. \(\cos(\arcsin(-\dfrac{1}{5}))\)
5. \(\sin(\arccos(-\dfrac{3}{5}))\)

Contestar

2. Vamos\(\theta = \cos^{-1}(\dfrac{2}{3})\). Entonces\(\cos(\theta) = \dfrac{2}{3}\) y\(0 \leq \theta \leq \pi\). Entonces\(\sin(\theta) > 0\) y\(\sin^{2}(\theta) = 1 - \cos^{2}(\theta) = \dfrac{5}{9}\). Entonces

\[\tan(\cos^{-1}(\dfrac{2}{3})) = \tan(\theta) = \dfrac{\sin(\theta)}{\cos(\theta)} = \dfrac{\dfrac{\sqrt{5}}{3}}{\dfrac{2}{3}} = \dfrac{\sqrt{5}}{2}\]

Usando una calculadora, obtenemos

\[\tan(\cos^{-1}(\dfrac{2}{3})) \approx 1.11803\]y\[\dfrac{\sqrt{5}}{2} \approx 1.11803\]

Ejercicio\(\PageIndex{6}\)

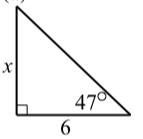
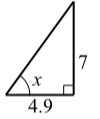
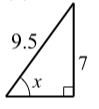
Para cada uno de los siguientes triángulos rectos, determine el valor de\(x\) correcto a la milésima más cercana.

1. 
2. 
3. 
4. 

Contestar

1. \(x = 6\tan(47^\circ) \approx 6.434\).
2. \(x = 3.1\cos(67^\circ) \approx 1.211\).
3. \(x = \tan^{-1}(\dfrac{7}{4.9}) \approx 55.008^\circ\).
4. \(x = \sin^{-1}(\dfrac{7}{9.5}) \approx 47.463^\circ\).

Ejercicio\(\PageIndex{7}\)

Un ángulo en un triángulo recto es\(55^\circ\) y el lado opuesto a ese ángulo es de 10 pies de largo. Determinar la longitud del otro lado, la longitud de la hipotenusa y la medida del otro ángulo agudo.

Ejercicio\(\PageIndex{8}\)

Un ángulo en un triángulo rectángulo es\(37.8^\circ\) y la longitud de la hipotenusa es de 25 pulgadas. Determinar la longitud de los otros dos lados del triángulo rectángulo.

Ejercicio\(\PageIndex{9}\)

Un ángulo en un triángulo rectángulo es\(27^\circ 12'\) y la longitud del lado adyacente a este ángulo es de 4 pies. Determinar el otro ángulo agudo en el triángulo, la longitud del lado opuesto a este ángulo, y la longitud de la hipotenusa.
Nota: La notación significa que el ángulo es de 27 grados, 12 segundos. Recuerda que 1 segundo es\(\dfrac{1}{60}\) de grado.

Contestar

El otro ángulo agudo es\(64^\circ 48'\).

El lado opuesto al\(27^\circ 12'\) ángulo son\(4\tan(27^\circ 12') \approx 2.056\) pies.

La hipotenusa es\(\dfrac{4}{\cos(27^\circ 12')} \approx 4.497\) pies.

Tenga en cuenta que el Teorema de Pitágoras se puede utilizar para verificar los resultados mostrando eso\(4^{2} + 2.056^{2} \approx 4.497^{2}\). La comprobación no será exacta porque las\(2.056\) y\(4.497\) son aproximaciones de los valores exactos.

Ejercicio\(\PageIndex{10}\)

Si sólo conocemos las medidas de los tres ángulos de un triángulo rectángulo, ex- llano por qué no es posible determinar las longitudes de los lados de este triángulo rectángulo.

Ejercicio\(\PageIndex{11}\)

Supongamos que conocemos la medida\(\theta\) de uno de los ángulos agudos en un triángulo rectángulo y conocemos la longitud\(x\) del lado opuesto al ángulo\(\theta\). Explicar cómo determinar la longitud del lado adyacente al ángulo\(\theta\) y la longitud de la hipotenusa.

Ejercicio\(\PageIndex{12}\)

En el diagrama de la derecha, determine los valores de\(a\),\(b\), y\(h\) a la milésima más cercana.
Los valores dados son:

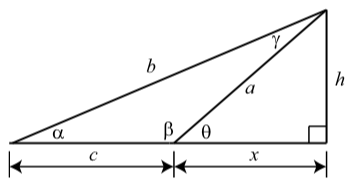
Figura\(\PageIndex{1}\)

\[\alpha = 23^\circ\]

\[\beta = 140^\circ\]

\[c = 8\]

Contestar

Primero señalamos eso\(\theta = 40^\circ\). Utilizamos las siguientes dos ecuaciones para determinar\(x\).

\[\tan(\alpha) = \dfrac{h}{c + x}\]\[\tan(x) = \dfrac{h}{x}\]

Sustituir\(h = x\tan(\theta)\) en la primera ecuación y resolver por\(x\) da\[x = \dfrac{c\tan(\alpha)}{\tan(\theta) - \tan(\alpha)} \approx 8.190.\]

Luego podemos usar triángulos rectos para obtener\(h \approx 6.872\space ft, a \approx 10.691\space ft, and b \approx 17.588\space ft\)

Ejercicio\(\PageIndex{13}\)

Un árbol alto de hoja perenne ha sido dañado por un fuerte viento. La parte superior del árbol está agrietada y doblada, tocando el suelo como si el tronco estuviera abisagrado. La punta del árbol toca el suelo a 20 pies y 6 pulgadas de la base del árbol (donde el árbol y el suelo se encuentran). La punta del árbol forma un ángulo de 17 grados donde toca el suelo. Determinar la altura original del árbol (antes de que se rompiera) a la décima de pie más cercana. Supongamos que la base del árbol es perpendicular al suelo.

Ejercicio\(\PageIndex{14}\)

Supongamos que una persona está parada en lo alto de un edificio y que tiene un instrumento que le permite medir ángulos de depresión. Hay dos puntos que están a 100 pies de distancia y se encuentran en una línea recta que es perpendicular a la base del edificio.

Ahora supongamos que mide el ángulo de depresión al punto más cercano a ser\(35.5^\circ\) y que mide el ángulo de depresión al otro punto a ser\(29.8^\circ\). Determinar la altura del edificio.

Ejercicio\(\PageIndex{15}\)

Una empresa cuenta con una escalera de 35 pies que utiliza para limpiar las ventanas de su edificio. Por razones de seguridad, la escalera nunca debe hacer un ángulo de más que\(50^\circ\) con el suelo.

1. Cuál es la mayor altura que puede alcanzar la escalera en el edificio si el ángulo que hace con el suelo no es mayor que\(50^\circ\).
2. Supongamos que el edificio tiene 40 pies de altura. Nuevamente, siguiendo las pautas de seguridad, ¿qué longitud de escalera se necesita para que la escalera llegue a la parte superior del edificio?

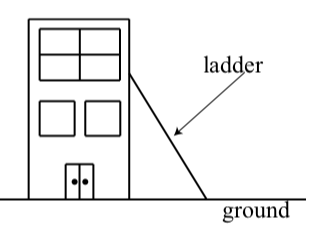
Figura\(\PageIndex{2}\)

Nota

Para Ejercicios\(\PageIndex{16}\) a través de\(\PageIndex{19}\), use la Ley de los Senos.

Ejercicio\(\PageIndex{16}\)

Dos ángulos de un triángulo son\(42^\circ\) y\(73^\circ\). El lado opuesto al\(73^\circ\) ángulo es de 6.5 pies de largo. Determinar el tercer ángulo del triángulo y las longitudes de los otros dos lados.

Contestar

El tercer ángulo es\(65^\circ\). El lado opuesto al\(42^\circ\) ángulo es de\(4.548\) pies de largo. El lado opuesto al\(65^\circ\) ángulo es de\(6.160\) pies de largo.

Ejercicio\(\PageIndex{17}\)

Un triángulo tiene un lado que tiene 4.5 metros de largo y este lado es adyacente a un ángulo de\(110^\circ\). Además, el lado opuesto al\(110^\circ\) ángulo tiene 8 metros de largo. Determinar los otros dos ángulos del triángulo y la longitud del tercer lado.

Ejercicio\(\PageIndex{18}\)

Un triángulo tiene un lado que mide 5 pulgadas de largo que es adyacente a un ángulo de\(61^\circ\). El lado opuesto al\(61^\circ\) ángulo es de 4.5 pulgadas de largo. Determinar los otros dos ángulos del triángulo y la longitud del tercer lado.

Contestar

Hay dos triángulos que satisfacen estas condiciones. El seno del ángulo opuesto al lado de la\(5\) pulgada es aproximadamente\(0.9717997\).

Ejercicio\(\PageIndex{19}\)

En un triángulo dado, el lado opuesto a un ángulo de\(107^\circ\) tiene 18 pulgadas de largo. Uno de los lados adyacentes al\(107^\circ\) ángulo mide 15.5 pulgadas de largo. Determinar los otros dos ángulos del triángulo y la longitud del tercer lado.

Nota

Para Ejercicios\(\PageIndex{20}\) a través de\(\PageIndex{21}\), utilizar la Ley de Cosinos.

Ejercicio\(\PageIndex{20}\)

Los tres lados de un triángulo miden 9 pies de largo, 5 pies de largo y 7 pies de largo. Determinar los tres ángulos del triángulo.

Contestar

El ángulo opuesto al lado largo del\(9\) pie es\(95.739^\circ\). El ángulo opuesto al lado largo del\(7\) pie es\(50.704^\circ\). El ángulo opuesto al lado largo del\(5\) pie es\(33.557^\circ\).

Ejercicio\(\PageIndex{21}\)

Un triángulo tiene dos lados de longitudes 8.5 metros y 6.8 metros. El ángulo formado por estos dos lados es\(102^\circ\). Determinar la longitud del tercer lado y los otros dos ángulos del triángulo

Nota

Para los ejercicios restantes, utilice un método adecuado para resolver el problema.

Ejercicio\(\PageIndex{22}\)

Dos ángulos de un triángulo son\(81.5^\circ\) y\(34^\circ\). La longitud del lado opuesto al tercer ángulo es de 8.8 pies. Determinar el tercer ángulo y las longitudes de los otros dos lados del triángulo.

Ejercicio\(\PageIndex{23}\)

En el siguiente diagrama, determine el valor de\(\gamma\) (a la centésima de grado más cercana) y determine los valores de\(h\) y\(d\) (a la milésima más cercana) si se le da que\[a = 4\]\[b = 8\]\[c = 10\]\[\theta = 26^\circ\]

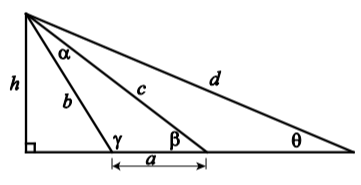
Figura\(\PageIndex{3}\)

Ejercicio\(\PageIndex{24}\)

En el siguiente diagrama, se da que:

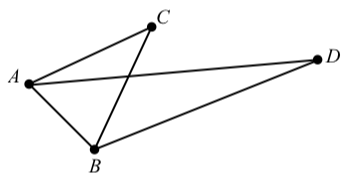
Figura\(\PageIndex{4}\)

• La longitud de\(AC\) es\(2\).
• La longitud de\(BC\) es\(2\).
• \(\angle ACB = 40^\circ\)
• \(\angle CAD = 20^\circ\)
• \(\angle CBD = 45^\circ\)

Determinar las longitudes de\(AB\) y\(AD\) a la milésima más cercana.

Ejercicio\(\PageIndex{25}\)

Se va a construir un remonte a lo largo de la ladera de una montaña de punto\(A\) a punto\(B\) en el siguiente diagrama. Deseamos determinar la longitud de este remonte.

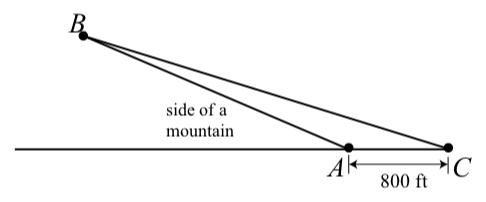
Figura\(\PageIndex{5}\)

Un topógrafo determina la medición del ángulo\(BAC\) a ser\(155.6^\circ\) y luego mide una distancia de 800 pies de Punto\(A\) a Punto\(C\). Finalmente, determina la medida del ángulo\(BCA\) a ser\(17.2^\circ\). ¿Cuál es la longitud del telesilla (de punto\(A\) a punto\(B\))?

Contestar

El remonte mide unos\(1887.50\) pies de largo.

Ejercicio\(\PageIndex{26}\)

Un barco navega desde Muskegon con destino a Chicago, una distancia de navegación de 121 millas. El barco mantiene una velocidad constante de 15 millas por hora. Después de encontrarse con fuertes vientos cruzados, la tripulación se encuentra fuera de rumbo\(20^\circ\) después de 4 horas. Una imagen cruda se muestra en el siguiente diagrama, donde\(\alpha = 20^\circ\).

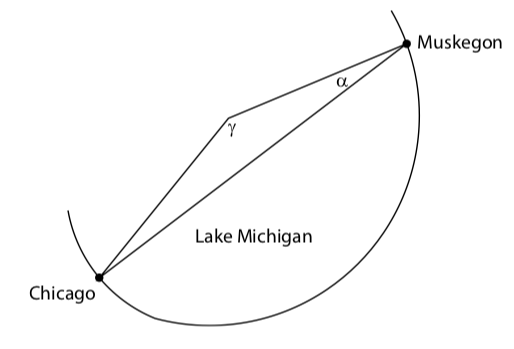
Figura\(\PageIndex{6}\)

1. ¿A qué distancia está el velero de Chicago en este momento?
2. ¿Cuál es la medida de grado del ángulo\(\gamma\) (al décimo más cercano) en el diagrama? ¿A través de qué ángulo debe girar el barco para corregir su rumbo y dirigirse directo a Chicago?
3. Suponiendo que el barco mantenga una velocidad de\(15\) millas por hora, ¿cuánto tiempo han agregado a su viaje al estar fuera de rumbo?

Contestar

1. El barco está\(67.8\) a unos kilómetros de Chicage.
2. \(\gamma \approx 142.4^\circ\). Entonces el barco debe girar a través de un ángulo de aproximadamente\(180^\circ - 142.4^\circ = 37.6^\circ\)
3. El viaje directo de Muskegon a Chicago tomaría\(\dfrac{121}{15}\) horas o aproximadamente\(8.07\) horas. Al salir del curso, el viaje ahora tomará\(\dfrac{127.8}{15}\) horas o aproximadamente\(8.52\) horas.

Ejercicio\(\PageIndex{27}\)

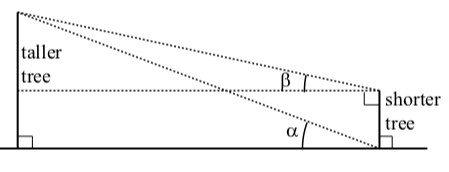
Figura\(\PageIndex{7}\)

Dos árboles están en lados opuestos de un río. Se sabe que la altura más alta del menor de los dos árboles es\(13\) metros. Una persona realiza las siguientes medidas de ángulo:

El ángulo de elevación desde la base del árbol más corto hasta la parte superior del árbol más alto es\(\alpha = 20^\circ\).

El ángulo de elevación desde la parte superior del árbol más corto hasta la parte superior del árbol más alto es\(\beta = 12^\circ\).

Determinar la distancia entre las bases de los dos árboles y la altura del árbol más alto.

Ejercicio\(\PageIndex{28}\)

Una de las Siete Maravillas del Mundo originales, la Gran Pirámide de Giza (también conocida como la Pirámide de Khufu o la Pirámide de Keops), se creía que fue construida en un período de\(10\) hasta un\(20\) año concluyendo alrededor de\(2560\) B.C.E. También se cree que la altura original de la pirámide era \(146.5\)metros pero que ahora es más corto debido a la erosión y la pérdida de algunas piedras más altas.

Para determinar su altura actual, se midió el ángulo de elevación desde una distancia de\(30\) metros de la base de la pirámide para ser\(46.12^\circ\), y luego se midió el ángulo de elevación para ser\(40.33^\circ\) desde una distancia de\(60\) metros de la base de la pirámide como se muestra en lo siguiente diagrama. Usa esta información para determinar la altura\(h\) de la pirámide. (\(138.8\)metros)

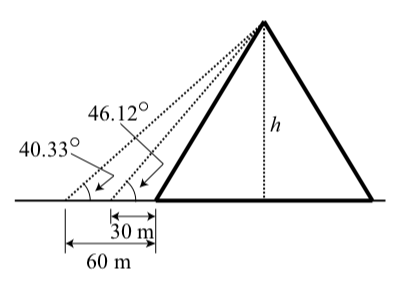
Figura\(\PageIndex{8}\)

Ejercicio\(\PageIndex{29}\)

Dos lados de un triángulo tienen\(2.5\) metros de longitud y\(3.5\) metros, y el ángulo formado por estos dos lados tiene una medida de\(60^\circ\). Determinar el área del triángulo. Nota: Este es el triángulo en Progreso Comprobación 3.17 en la página 200.

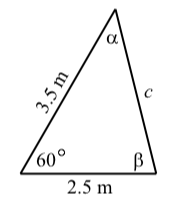
Figura\(\PageIndex{9}\)

Ejercicio\(\PageIndex{30}\)

Un campo tiene la forma de un cuadrilátero que no es un paralelogramo. Como se muestra en el siguiente diagrama, tres lados miden\(50\) yardas,\(60\) yardas y\(70\) yardas. Debido a algún humedal a lo largo del cuarto lado, la longitud del cuarto lado no se pudo medir directamente. Los dos ángulos mostrados en el diagrama miden\(127^\circ\) y\(132^\circ\).

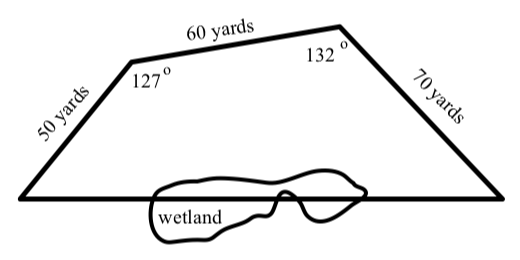
Figura\(\PageIndex{10}\)

Determinar la longitud del cuarto lado del cuadrilátero, las medidas de los otros dos ángulos en el cuadrilátero y el área del cuadrilátero. Las longitudes deben ser precisas a la centésima de yarda más cercana, las medidas del ángulo deben ser correctas a la centésima de grado más cercana, y el área debe ser correcta a la centésima de yarda cuadrada más cercana.

Ejercicio\(\PageIndex{31}\)

En cada uno de los siguientes diagramas, uno de los vectores\(\textbf{u}\),\(\textbf{v}\), y\(\textbf{u} + \textbf{v}\) está etiquetado. Etiquetar los vectores los otros dos vectores para hacer del diagrama una representación válida de\(\textbf{u} + \textbf{v}\)

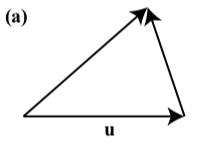
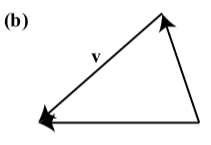
Contestar

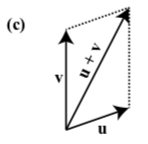
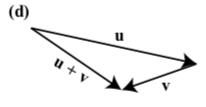
Ejercicio\(\PageIndex{32}\)

En el siguiente diagrama, dibuje los vectores\(\textbf{u} + \textbf{v}\),\(\textbf{u} - \textbf{v}\),\(2\textbf{u} + \textbf{v}\), y\(2\textbf{u} - \textbf{v}\).

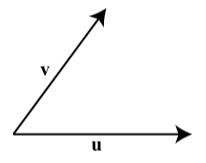
Figura\(\PageIndex{11}\)

Contestar

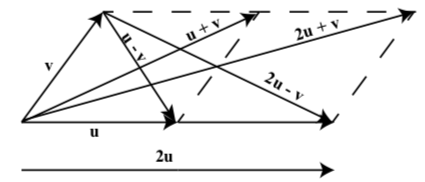
Figura\(\PageIndex{12}\)

Ejercicio\(\PageIndex{33}\)

En el siguiente diagrama,\(|\textbf{a}| = 10\) y\(|\textbf{a}| + |\textbf{b}| = 14\). Además, el ángulo\(\theta\) entre los vectores\(\textbf{a}\) y\(\textbf{b}\) es\(30^\circ\). Determinar la magnitud del vector\(\textbf{b}\) y el ángulo entre los vectores\(\textbf{a}\) y\(\textbf{a} + \textbf{b}\).

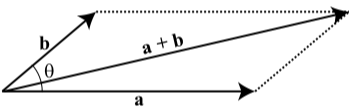
Figura\(\PageIndex{13}\)

Contestar

El ángulo entre los vectores\(\textbf{a}\) y\(\textbf{a} + \textbf{b}\) es aproximadamente\(9.075^\circ\). Además,\(|\textbf{b}| \approx 4.416\).

Ejercicio\(\PageIndex{34}\)

Supongamos que\(\textbf{a}\) los vectores y\(\textbf{b}\) tienen magnitudes de 125 y 180, respectivamente. También supongamos que el ángulo entre estos dos vectores es\(35^\circ\). Determinar la magnitud del vector\(\textbf{a} + \textbf{b}\) y la medida del ángulo entre los vectores\(\textbf{a}\) y\(\textbf{a} + \textbf{b}\).

Ejercicio\(\PageIndex{35}\)

Un automóvil que pesa\(3250\) libras se encuentra en un plano inclinado que hace un ángulo de\(4.5^\circ\) con la horizontal. Determinar la magnitud de la fuerza del automóvil en el plano inclinado, y determinar la magnitud de la fuerza sobre el automóvil hacia abajo del avión debido a la gravedad. ¿Cuál es la magnitud de la fuerza más pequeña necesaria para evitar que el automóvil ruede por el avión?

Ejercicio\(\PageIndex{36}\)

Un experimento determinó que una fuerza de\(45\) libras es necesaria para evitar que un objeto\(250\) libra se deslice por un plano inclinado. Determinar el ángulo que hace el plano inclinado con la horizontal.

Ejercicio\(\PageIndex{37}\)

Un cable que puede soportar una fuerza de\(4500\) libras se utiliza para tirar de un objeto hacia arriba por un plano inclinado que forma un ángulo de 15 grados con la horizontal. ¿Cuál es el objeto más pesado que se puede levantar por este avión con el cable? (Supongamos que la fricción puede ser ignorada.)

Ejercicio\(\PageIndex{38}\)

Determinar la magnitud y el ángulo de dirección de cada uno de los siguientes vectores.

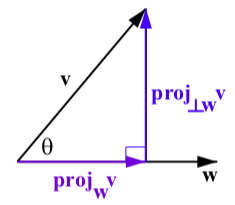
Figura\(\PageIndex{14}\): La\(\textbf{v}\) proyección de\(\textbf{w}\)

1. \[\textbf{v} = 3\textbf{i} + 5\textbf{j}\]
2. \[\textbf{w} = \langle -3, 6 \rangle\]
3. \[\textbf{a} = 4\textbf{i} - 7\textbf{j}\]
4. \[\textbf{u} = \langle -3, -5 \rangle\]

Contestar

1. \(|\textbf{v}| = \sqrt{34}\). El ángulo de dirección es aproximadamente\(59.036^\circ\).
2. \(|\textbf{w}| = \sqrt{45}\). El ángulo de dirección es aproximadamente\(116.565^\circ\).

Ejercicio\(\PageIndex{39}\)

Determinar los componentes horizontal y vertical de cada uno de los siguientes vectores. Escribe cada vector en\(\textbf{i}\),\(\textbf{j}\) forma.

El vector\(\textbf{v}\) con magnitud 12 y ángulo de dirección\(50^\circ\)?

El vector\(\textbf{u}\) con\(\textbf{u} = \sqrt{20}\) y ángulo de dirección\(125^\circ\).

El vector\(\textbf{w}\) con magnitud\(5.25\) y ángulo de dirección\(200^\circ\).

Contestar

1. \(\textbf{v} = 12\cos(50^\circ) + 12\sin(50^\circ) \approx 7.713\textbf{i} + 9.193\textbf{j}\).
2. \(\textbf{u} = \sqrt{20}\cos(125^\circ) + \sqrt{20}\sin(125^\circ) \approx -2.565\textbf{i} + 3.663\textbf{j}\)

Ejercicio\(\PageIndex{40}\)

Vamos\(\textbf{u} = 2\textbf{i} + 3\textbf{j}\),\(\textbf{v} = -\textbf{i} + 5\textbf{j}\), y\(\textbf{w} = 4\textbf{i} - 2\textbf{j}\). Determinar la\(\textbf{i}\)\(\textbf{j}\) forma de cada uno de los siguientes:

1. \[5\textbf{u} - \textbf{v}\]
2. \[2\textbf{v} + 7\textbf{w}\]
3. \[\textbf{u} + \textbf{v} + \textbf{w}\]
4. \[3\textbf{u} + 5\textbf{w}\]

Contestar

1. \(5\textbf{u} - \textbf{v} = 11\textbf{i} + 10\textbf{j}\)

3. \(\textbf{u} + \textbf{v} + \textbf{w} = 5\textbf{i} + 6\textbf{j}\)

Ejercicio\(\PageIndex{41}\)

Determinar el valor del producto punto para cada uno de los siguientes pares de vectores.

1. \(\textbf{v} = 2\textbf{i} + 5\textbf{j}\)y\(\textbf{w} = 3\textbf{i} - 2\textbf{j}\)
2. \(\textbf{a}\)y\(\textbf{b}\) dónde\(|\textbf{a}| = 6\),\(|\textbf{w}| = 3\), y el ángulo entre\(\textbf{v}\) y\(\textbf{w}\) es\(30^\circ\)
3. \(\textbf{a}\)y\(\textbf{b}\) dónde\(|\textbf{a}| = 6\),\(|\textbf{w}| = 3\), y el ángulo entre\(\textbf{v}\) y\(\textbf{w}\) es\(150^\circ\)
4. \(\textbf{a}\)y\(\textbf{b}\) dónde\(|\textbf{a}| = 6\),\(|\textbf{w}| = 3\), y el ángulo entre\(\textbf{v}\) y\(\textbf{w}\) es\(50^\circ\)
5. \(\textbf{a} = 5\textbf{i} - 2\textbf{j}\)y\(\textbf{b} = 2\textbf{i} + 5\textbf{j}\)

Contestar

1. \(\textbf{v}\cdot\textbf{w} = -4\).

2. \(\textbf{a}\cdot\textbf{b} = 9\sqrt{3}\).

Ejercicio\(\PageIndex{42}\)

Determinar el ángulo entre cada uno de los siguientes pares de vectores.

1. \[\textbf{v} = 2\textbf{i} + 5\textbf{j}\]y\[\textbf{w} = 3\textbf{i} - 2\textbf{j}\]
2. \[\textbf{a} = 5\textbf{i} - 2\textbf{j}\]y\[\textbf{b} = 2\textbf{i} + 5\textbf{j}\]
3. \[\textbf{v} = 3\textbf{i} - 2\textbf{j}\]y\[\textbf{w} = -\textbf{i} + 4\textbf{j}\]

Contestar

1. El ángulo entre\(\textbf{v}\) y\(\textbf{w}\) es\(\cos^{-1}(\dfrac{-4}{\sqrt{29}\sqrt{13}}) \approx 101.89^\circ\).

Ejercicio\(\PageIndex{43}\)

Para cada par de vectores\(\textbf{proj}_{\textbf{v}}\textbf{w}\), determine\(\textbf{proj}_{\perp\textbf{v}}\textbf{w}\) y verifique que

\(\textbf{w} = \textbf{proj}_{\perp\textbf{w}}\textbf{v} + \textbf{proj}_{\textbf{w}}\textbf{v}\). Dibuja un cuadro que muestre todos los vectores involucrados en esto.

1. \[\textbf{v} = 2\textbf{i} + 5\textbf{j}\]y\[\textbf{w} = 3\textbf{i} - 2\textbf{j}\]
2. \[\textbf{v} = \langle -2, 3 \rangle\]y\[\textbf{w} = \langle 1, 1 \rangle\]

Contestar

1. \[\textbf{proj}_{v}\textbf{w} = \dfrac{\textbf{w}\cdot \textbf{v}}{\textbf{v}\cdot \textbf{v}}\textbf{v} = \dfrac{-4}{29}(2\textbf{i} + 5\textbf{j}) = -\dfrac{8}{29}\textbf{i} - \dfrac{20}{29}\textbf{j}\]

\[\textbf{proj}_{\perp_\textbf{v}}\textbf{w} = \textbf{w} - \textbf{proj}_{v}\textbf{w} = \dfrac{95}{29}\textbf{i} - \dfrac{38}{29}\textbf{j}\]