3.6: Vectores desde un punto de vista algebraico

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

• ¿Cómo encontramos la forma componente de un vector?
• ¿Cómo encontramos la magnitud y la dirección de un vector escrito en forma de componente?
• ¿Cómo sumamos y restamos vectores escritos en forma de componente y cómo encontramos el producto escalar de un vector escrito en forma de componente?
• ¿Cuál es el producto dot de dos vectores?
• ¿Qué nos dice el producto punto sobre el ángulo entre dos vectores?
• ¿Cómo encontramos la proyección de un vector sobre otro?

Introducción y Terminología

Hemos visto que un vector está completamente determinado por la magnitud y la dirección. Entonces dos vectores que tienen la misma magnitud y dirección son iguales. Eso significa que podemos posicionar nuestro vector en el plano e identificarlo de diferentes maneras. Por un lado, podemos colocar la punta de un vector\(\textbf{v}\) en el origen y la cola terminará en algún momento\((v_{1}, v_{2})\) como se ilustra en la Figura\(\PageIndex{1}\).

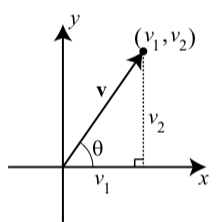
Figura\(\PageIndex{1}\): Un vector en posición estándar

Se dice que un vector con su punto inicial en el origen está en posición estándar y es representado por\(\textbf{v} = \langle v_{1}, v_{2} \rangle\). Tenga en cuenta la importante distinción en notación entre el vector\(\textbf{v} = \langle v_{1}, v_{2} \rangle\) y el punto\((v_{1}, v_{2})\). Las coordenadas del punto terminal\((v_{1}, v_{2})\) se denominan los componentes del vector\(\textbf{v}\). Llamamos a\(\textbf{v} = \langle v_{1}, v_{2} \rangle\) la forma componente del vector\(\textbf{v}\). La primera coordenada\(\textbf{v}_{1}\) se llama\(x\) -componente o componente horizontal del vector\(\textbf{v}\), y la primera coordenada\(\textbf{v}_{2}\) se llama\(y\) -componente o componente vertical del vector\(\textbf{v}\). El ángulo no negativo\(\theta\) entre el vector y el\(x\) eje positivo (con\(0 \leq \theta \leq 360^\circ\)) se denomina ángulo de dirección del vector. Ver Figura\(\PageIndex{1}\).

Uso de vectores de base

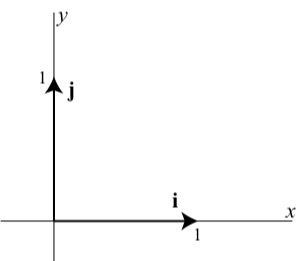
Hay otra manera de escribir algebraicamente un vector si se conocen los componentes del vector. Esto utiliza los llamados vectores base estándar para los vectores en el plano. Estos dos vectores se denotan por\(\textbf{i}\) y\(\textbf{j}\) y se definen de la siguiente manera y se muestran en el diagrama siguiente.

\(\textbf{i} = \langle 1, 0 \rangle\)y\(\textbf{j} = \langle 0, 1 \rangle\)

El diagrama de la Figura 3.28 muestra cómo usar los vectores\(\textbf{i}\) y\(\textbf{j}\) representar un vector\(\textbf{v} = \langle a, b \rangle\).

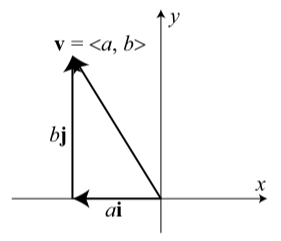
Figura\(\PageIndex{2}\): Usando los Vectores\(\textbf{i}\) y\(\textbf{j}\)

El diagrama muestra que si colocamos la base del vector\(\textbf{j}\) en la punta del vector\(\textbf{i}\), vemos que\[\textbf{v} = \langle a, b \rangle = a\textbf{i} + b\textbf{j}\]

Esto a menudo se llama la\(\textbf{j}\) forma\(\textbf{i}\), de un vector, y el número real\(a\) se llama el componente\(\textbf{i}\) - de\(\textbf{v}\) y el número real\(b\) se llama el componente\(\textbf{j}\) - de\(\textbf{v}\)

Fórmulas algebraicas para propiedades geométricas de un vector

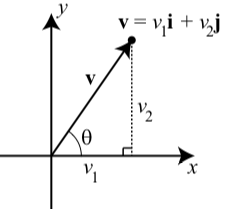
Los vectores tienen ciertas propiedades geométricas como la longitud y un ángulo de dirección. Con el uso de la forma componente de un vector, podemos escribir fórmulas algebraicas para estas propiedades. Usaremos el diagrama a la derecha para ayudar a explicar estas fórmulas.

• La magnitud (o longitud) del vector\(\textbf{v}\) es la distancia desde el origen hasta el punto\((v_{1}, v_{2})\) y así\[|\textbf{v}| = \sqrt{v_{1}^{2} + v_{2}^{2}}\]
• El ángulo de dirección de\(\textbf{v}\) es\(0 \leq \theta < 360^\circ\), dónde\[\cos(\theta) = \dfrac{v_{1}}{|\textbf{v}|}\] y\[\sin(\theta) = \dfrac{v_{2}}{|\textbf{v}|}\]
• La componente horizontal y componente y vertical del vector\(\textbf{v}\) y el ángulo de dirección\(\theta\) son\[v_{1} = |\textbf{v}|\cos(\theta)\] y\[v_{2} = |\textbf{v}|\sin(\theta)\]

Ejercicio\(\PageIndex{1}\)

1. Supongamos que el componente horizontal de un vector\(\textbf{v}\) es 7 y el componente vertical es\(-3\). Así que tenemos\(\textbf{v} = 7\textbf{i} + (-3)\textbf{j} = 7\textbf{i} - 3\textbf{j}\). Determinar la magnitud y el ángulo de dirección de\(\textbf{v}\).
2. Supongamos que un vector\(\textbf{w}\) tiene una magnitud de 20 y un ángulo de dirección de\(-200^\circ\). Determinar los componentes horizontales y verticales de\(\textbf{w}\) y escribir\(\textbf{w}\) en\(\textbf{i}\)\(\textbf{j}\) forma.

Contestar

1. \(\textbf{v} = 7\textbf{i} + (-3)\textbf{j}\). Entonces\(|\textbf{v}| = \sqrt{7^{2} + (-3)^{2}} = \sqrt{58}\). Además,\[\cos(\theta) = \dfrac{7}{\sqrt{58}}\space\text{and}\space\sin(\theta) = \dfrac{-3}{\sqrt{58}}\]

Entonces el lado terminal de\(\theta\) está en el cuarto cuadrante, y podemos escribir\[\theta = 360^\circ - \arccos(\dfrac{7}{\sqrt{58}}).\] So\(\theta \approx 336.80^\circ\).

2. Nos dan\(|\textbf{w}| = 20\) y el ángulo\(\theta\) de dirección de\(\textbf{w}\) es\(200^\circ\). Entonces, si escribimos\(\textbf{w} = w_{1}\textbf{i} + w_{2}\textbf{j}\). Entonces

\[w_{1} = 20\cos(200^\circ) \approx -1.794\]

\[w_{1} = 20\cos(200^\circ) \approx -6.840\]

Operaciones en vectores

En la Sección 3.5 aprendimos a sumar dos vectores y a multiplicar un vector por un escalar. En ese momento, las descripciones de estas operaciones eran de naturaleza geométrica. Ahora conocemos la forma componente de un vector. Entonces una buena pregunta es: “¿Podemos usar la forma componente de vectores para sumar vectores y multiplicar un vector por un escalar?”

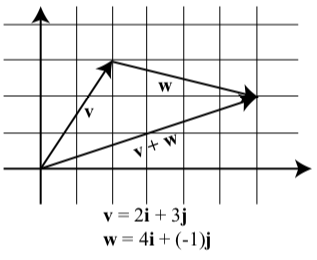
Para ilustrar la idea, veremos el Avance Check 3.25 en la página 223, donde agregamos dos vectores\(\textbf{v}\) y\(\textbf{w}\). Aunque no utilizamos las formas componentes de estos vectores, ahora podemos ver eso\[\textbf{v} = \langle 2, 3 \rangle = 2\textbf{i} + 3\textbf{j}\] y\[\textbf{w} = \langle 4, -1 \rangle = 4\textbf{i} + (-1)\textbf{j}\]

El diagrama anterior formaba parte de las soluciones para esta comprobación de progreso pero ahora muestra los vectores en un plano de coordenadas.

Observe que\[\textbf{v} + \textbf{w} = 6\textbf{i} + 2\textbf{j}\]\[\textbf{v} + \textbf{w} = (2 + 4)\textbf{i} + (3 + (-1))\textbf{j}\]

La Figura 3.29 muestra un diagrama más general con\[\textbf{v} = \langle a, b \rangle = a\textbf{i} + b\textbf{j}\]\[\textbf{w} = \langle c, d \rangle = c\textbf{i} + d\textbf{j}\]

en posición estándar. Este diagrama muestra que el punto terminal de\(\textbf{v} + \textbf{w}\) en posición estándar es\((a + c, b + d)\) y así

\[\textbf{v} + \textbf{w} = \langle a + c, b + d \rangle = (a + c)\textbf{i} + (b + d)\textbf{j}\]

Esto significa que podemos agregar dos vectores sumando sus componentes horizontales y sumando sus componentes verticales. La siguiente comprobación de progreso ilustrará algo similar para la multiplicación escalar.

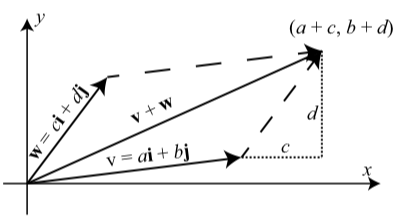
Figura\(\PageIndex{3}\): La suma de dos vectores

Ejercicio\(\PageIndex{2}\)

Vamos\(\textbf{v} = \langle 3, -2 \rangle\). Dibuja el vector v en posición estándar y luego dibuja los vectores\(2\textbf{v}\) y\(-2\textbf{v}\) en posición estándar. ¿Cuáles son las formas componentes de los vectores\(2\textbf{v}\) y\(-2\textbf{v}\)?

En general, ¿cómo crees que\(c\) debería definirse un múltiplo escalar de un vector\(\textbf{a} = \langle a_{1}, a_{2} \rangle\) por un escalar? Escribe una definición formal de un múltiplo escalar de un vector basado en tu intuición.

Contestar

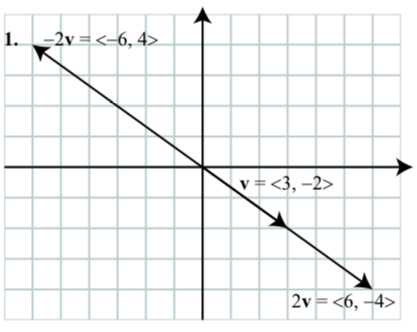
2. Para un vector\(\textbf{a} = \langle a_{1}, a_{2} \rangle\) y un escalar\(c\), definimos que el múltiplo\(c\textbf{a}\) escalar sea\[c\textbf{a} = \langle ca_{1}, ca_{2} \rangle.\]

Con base en el trabajo que hemos realizado, hacemos las siguientes definiciones formales.

Definición

Para vectores\(\textbf{v} = \langle v_{1}, v_{2} \rangle = v_{1}\textbf{i} + v_{2}\textbf{j}\)\(\textbf{w} = \langle w_{1}, w_{2} \rangle = w_{1}\textbf{i} + w_{2}\textbf{j}\) y y escalar\(c\), hacemos la siguiente definición:

\[\textbf{v} + \textbf{w} = \langle v_{1} + w_{1}, v_{2} + w_{2}\rangle\]
\[\textbf{v} + \textbf{w} = (v_{1} + w_{1})\textbf{i} + (v_{2} + w_{2})\textbf{j}\]
\[\textbf{v} - \textbf{w} = \langle v_{1} - w_{1}, v_{2} - w_{2}\rangle\]
\[\textbf{v} - \textbf{w} = (v_{1} - w_{1})\textbf{i} + (v_{2} - w_{2})\textbf{j}\]
\[c\textbf{v} = \langle cv_{1}, cv_{2}\rangle\]
\[c\textbf{v} = (cv_{1})\textbf{i} + (cv_{2})\textbf{j}\]

Ejercicio\(\PageIndex{3}\)

Vamos\(\textbf{u} = \langle 1, -2 \rangle\),\(\textbf{u} = \langle 0, 4 \rangle\), y\(\textbf{u} = \langle -5, 7 \rangle\).

1. Determinar la forma componente del vector\(2\textbf{u} - 3\textbf{v}\).
2. Determinar la magnitud y el ángulo de dirección para\(2\textbf{u} - 3\textbf{v}\).
3. Determinar la forma componente del vector u\(\textbf{u} + 2\textbf{v} - 7\textbf{w}\).

Contestar

Vamos\(\textbf{u} = \langle 1, -2 \rangle\), y\(\textbf{w} = \langle -5, 7 \rangle\).

1. \(2\textbf{u} - 3\textbf{v} = \langle 2, -4 \rangle - \langle 0, 12 \rangle = \langle 2, -16 \rangle\)

2. \(|2\textbf{u} - 3\textbf{v}| = \sqrt{2^{2} + (-16)^{2}} = \sqrt{260}\). Así que ahora deja\(\theta\) ser el ángulo de dirección de\(2\textbf{u} - 3\textbf{v}\). Entonces

\[\cos(\theta) = \dfrac{2}{\sqrt{260}}\space \text{and} \space \sin(\theta) = \dfrac{-16}{\sqrt{260}}.\]

Entonces el lado terminal de\(\theta\) está en el cuarto cuadrante. Eso lo vemos\(\arcsin(\dfrac{-16}{\sqrt{260}}) \approx -82.87^\circ\). Dado que el ángulo de dirección\(\theta\) debe satisfacer\(a \leq \theta < 360^circ\), eso lo vemos\(\theta \approx -82.87^\circ + 360^\circ \approx 277.13^\circ\).

3. \(\textbf{u} + 2\textbf{v} - 7\textbf{w} = \langle 1, -2 \rangle + \langle 0, 8 \rangle - \langle -35, 49 \rangle = \langle 36, -43 \rangle\).

El producto de punto de dos vectores

Encontrar soluciones óptimas a los sistemas es un problema importante en las matemáticas aplicadas. A menudo ocurre que no podemos encontrar una solución exacta que satisfaga ciertas restricciones, por lo que buscamos en cambio la “mejor” solución que satisfaga las limitaciones. Un ejemplo de esto es ajustar una curva de mínimos cuadrados a un conjunto de datos como hacen nuestras calculadoras al calcular una curva de regresión sinusoidal. El producto punto es útil en estas situaciones para encontrar las “mejores” soluciones a ciertos tipos de problemas. Aunque no lo veremos en este curso, tener colecciones de vectores perpendiculares es muy importante ya que permite cálculos rápidos y eficientes. El producto punto de los vectores nos permite medir el ángulo entre ellos y así determinar si los vectores son perpendiculares. El producto punto tiene muchas aplicaciones, por ejemplo, encontrar componentes de fuerzas que actúan en diferentes direcciones en física e ingeniería. Introducimos e investigamos productos dot en esta sección.

Hemos visto cómo sumar vectores y multiplicar vectores por escalares, pero aún no hemos introducido un producto de vectores. En general, un producto de vectores debería darnos otro vector, pero resulta que no hay una manera realmente útil de definir tal producto de vectores. Sin embargo, hay un punto “producto” de vectores cuya salida es un escalar en lugar de un vector, y el producto punto es un producto muy útil (aunque no sea un producto de vectores en un sentido técnico).

Recordemos que la magnitud (o longitud) del vector\(\textbf{u} = \langle u_{1}, u_{2} \rangle\) es:\[|\textbf{u}| = \sqrt{u_{1}^{2} + u_{2}^{2}} = \sqrt{u_{1}u_{1} + u_{2}u_{2}}\]

La expresión bajo la segunda raíz cuadrada es importante y la extendemos y le damos un nombre especial.

Definición

Dejar\(\textbf{u} = \langle u_{1}, u_{2} \rangle\) y\(\textbf{v} = \langle v_{1}, v_{2} \rangle\) ser vectores en el plano. El punto producto de\(\textbf{u}\) y\(\textbf{v}\) es el escalar\[\textbf{u}\cdot \textbf{v} = u_{1}v_{1} + u_{2}v_{2}.\]

Esto puede parecer un número extraño de calcular, pero resulta que el producto punto de dos vectores es útil para determinar el ángulo entre dos vectores. Recordemos que en Progreso Comprobación 3.27 en la página 225, se utilizó la Ley de Cosinos para determinar la suma de dos vectores y luego se utilizó la Ley de Sines para determinar el ángulo entre la suma y uno de esos vectores. Ahora hemos visto lo fácil que es calcular la suma de dos vectores cuando los vectores están en forma de componentes. El producto punto nos permitirá determinar el coseno del ángulo entre dos vectores en forma de componente. Esto se debe al siguiente resultado:

El producto de punto y el ángulo entre dos vectores

Si\(\theta\) es el ángulo entre dos vectores distintos de cero\(\textbf{u}\) y\(\textbf{v}\) (\(0^\circ \leq \theta \leq 180^\circ\)), entonces

\[\textbf{u}\cdot \textbf{v} = |\textbf{u}||\textbf{v}|\cos(\theta)\]o\[\cos(\theta) = \dfrac{\textbf{u}\cdot \textbf{v}}{|\textbf{u}||\textbf{v}|}\]

Observe que si hemos escrito los vectores\(\textbf{v}\) y\(\textbf{w}\) en forma de componentes, entonces tenemos fórmulas para calcular\(|\textbf{v}|, |\textbf{w}|\), y\(\textbf{v}\cdot \textbf{w}\). Este resultado puede parecer sorprendente pero es una consecuencia bastante directa de la Ley de Cosinos como ahora mostraremos. Dejar\(\theta\) ser el ángulo entre\(\textbf{u}\) y\(\textbf{v}\) como se ilustra en la Figura 3.30.

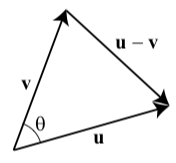
Figura\(\PageIndex{4}\): El ángulo entre\(\textbf{u}\) y\(\textbf{v}\)

Podemos aplicar la Ley de Cosinos para determinar el ángulo de la\(\theta\) siguiente manera:

\[|\textbf{u} - \textbf{v}|^{2} = |\textbf{u}|^{2} + |\textbf{v}|^{2} - 2|\textbf{u}||\textbf{v}|\cos(\theta)\]
\[(\textbf{u} - \textbf{v})\cdot (\textbf{u} - \textbf{v}) = |\textbf{u}|^{2} + |\textbf{v}|^{2} - 2|\textbf{u}||\textbf{v}|\cos(\theta)\]
\[(\textbf{u} \cdot \textbf{u}) -2(\textbf{u} \cdot \textbf{v}) + (\textbf{v} \cdot \textbf{v})= |\textbf{u}|^{2} + |\textbf{v}|^{2} - 2|\textbf{u}||\textbf{v}|\cos(\theta)\]
\[|\textbf{u}|^{2} -2(\textbf{u} \cdot \textbf{v}) + |\textbf{v}|^{2}= |\textbf{u}|^{2} + |\textbf{v}|^{2} - 2|\textbf{u}||\textbf{v}|\cos(\theta)\]
\[-2(\textbf{u} \cdot \textbf{u}) = -2|\textbf{u}||\textbf{v}|\cos(\theta)\]
\[\textbf{u} \cdot \textbf{u} = |\textbf{u}||\textbf{v}|\cos(\theta)\]

Ejercicio\(\PageIndex{4}\)

1. Determinar el ángulo\(\theta\) entre los vectores\(\textbf{u} = 3\textbf{i} + \textbf{j}\) y\(\textbf{v} = -5\textbf{i} + 2\textbf{j}\).

2. Determinar todos los vectores perpendiculares a\(\textbf{u} = \langle 1, 3 \rangle\). ¿Cuántos de esos vectores hay? Insinuación: Vamos\(\textbf{v} = \langle a, b \rangle\). ¿Bajo qué condiciones será el ángulo entre\(\textbf{u}\) y\(\textbf{v}\) será\(90^\circ\)?

Contestar

1. Si\(\theta\) es el ángulo entre\(\textbf{u} = 3\textbf{i} + \textbf{j}\) y\(\textbf{v} = -5\textbf{i} + 2\textbf{j}\), entonces

\[\cos(\theta) = \dfrac{\textbf{u}\cdot\textbf{v}}{|\textbf{u}||\textbf{v}|} = \dfrac{-13}{\sqrt{10}\sqrt{29}}\]

\[\theta = \cos^{-1}( \dfrac{-13}{\sqrt{10}\sqrt{29}})\]

así\(\theta \approx 139.764^\circ\).

2. Si\(\textbf{v} = \langle a, b \rangle\) es perpendicular a\(\textbf{u} = \langle 1, 3 \rangle\), entonces el ángulo\(\theta\) entre ellos es\(90^\circ\) y así\(\cos(\theta) = 0\). Entonces debemos tener\(\textbf{u}\cdot\textbf{v} = 0\) y esto significa que\(a + 3b = 0\). Entonces cualquier vector\(\textbf{v} = \langle a, b \rangle\) donde\(a = -3b\) será perpendicular a\(\textbf{v}\), y hay infinitamente muchos de esos vectores. Un vector perpendicular a\(\textbf{u}\) es\(\langle -3, 1 \rangle\).

Uno de los propósitos de la Comprobación de Progreso 3.34 fue usar la fórmula\[\cos(\theta) = \dfrac{\textbf{u}\cdot \textbf{v}}{|\textbf{u}||\textbf{v}|}\]

para determinar cuándo dos vectores son perpendiculares. Dos vectores\(\textbf{u}\) y\(\textbf{v}\) serán perpendiculares si y sólo si el ángulo\(\theta\) entre ellos es\(90^\circ\). Ya que\(\cos(90^\circ) = 0\), vemos que esta fórmula implica eso\(\textbf{u}\) y\(\textbf{v}\) será perpendicular si y sólo si\(\textbf{u}\cdot \textbf{v} = 0\) (Esto se debe a que una fracción será igual a\(0\) sólo cuando el numerador es igual a\(0\) y el denominador no es cero.) Así que tenemos:

Dos vectores son perpendiculares si y solo si su producto de punto es igual a\(0\).

Nota

Cuando dos vectores son perpendiculares, también decimos que son ortogonales.

Proyecciones

Otra aplicación útil del producto punto es encontrar la proyección de un vector sobre otro. Un ejemplo de dónde es útil dicho cálculo es el siguiente.

Usain Bolt de Jamaica emocionó al mundo del atletismo en 2008 con sus actuaciones récord mundial en la pista. Bolt ganó la carrera de 100 metros en un tiempo récord mundial de 9.69 segundos. Desde entonces ha mejorado ese tiempo con una carrera de 9.58 segundos con una asistencia de viento de 0.9 metros por segundo en Berlín el 16 de agosto de 20092. La asistencia del viento es una medida de la velocidad del viento que está ayudando a empujar a los corredores por la pista. Es mucho más fácil correr una carrera muy rápida si el viento sopla fuerte en la dirección de la carrera. Para que los récords mundiales no dependan de las condiciones climáticas, los tiempos solo se registran como tiempos récord si el viento que ayuda a los corredores es menor o igual a 2 metros por segundo. La velocidad del viento para una carrera es registrada por un medidor de viento que se configura cerca de la pista. Es importante señalar, sin embargo, que el clima no siempre es tan cooperativo como nos gustaría. El viento no siempre sopla exactamente en la dirección de la vía, por lo que el ancho debe dar cuenta del ángulo que hace el viento con la pista.

Si el viento sopla en la dirección del vector\(\textbf{u}\) y la pista está en la dirección del vector\(\textbf{v}\) en la Figura 3.31, entonces solo una parte del vector de viento total realmente está trabajando para ayudar a los corredores.

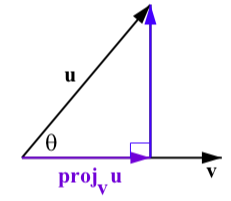
Figura\(\PageIndex{5}\): La\(\textbf{u}\) proyección de\(\textbf{v}\)

Esta parte se llama la proyección del vector\(\textbf{u}\) sobre el vector\(\textbf{v}\) y se denota\(\textbf{proj}_\textbf{v}\textbf{u}\).

Podemos encontrar esta proyección con un poco de trigonometría. Para ello, dejamos\(\theta\) ser el ángulo entre\(\textbf{u}\) y\(\textbf{v}\) como se muestra en la Figura\(\PageIndex{5}\). Usando trigonometría de triángulo rectángulo, vemos que\[|\textbf{proj}_\textbf{v}\textbf{u}| = |\textbf{u}|\cos(\theta) = |\textbf{u}|\dfrac{\textbf{u}\cdot \textbf{v}}{|\textbf{u}||\textbf{v}|} = \dfrac{\textbf{u}\cdot \textbf{v}}{|\textbf{v}|}\]
La cantidad que acabamos de derivar se llama la proyección escalar (o componente) de\(\textbf{u}\) onto\(\textbf{v}\) y se denota por\(\textbf{comp}_\textbf{v}\textbf{u}\). Así\(\textbf{comp}_\textbf{v}\textbf{u} = \dfrac{\textbf{u}\cdot \textbf{v}}{|\textbf{v}|}\)
Esto nos da la longitud de la proyección vectorial. Entonces, para determinar el vector, usamos un múltiplo escalar de esta longitud por un vector unitario en la misma dirección, que es\(\dfrac{1}{|\textbf{v}|}\textbf{v}\). Así obtenemos

\[\textbf{proj}_\textbf{v}\textbf{u} =|\textbf{proj}_\textbf{v}\textbf{u}|(\dfrac{1}{|\textbf{v}|}) = \dfrac{\textbf{u}\cdot \textbf{v}}{|\textbf{v}|}(\dfrac{1}{|\textbf{v}|}) = \dfrac{\textbf{u}\cdot \textbf{v}}{|\textbf{v}|^{2}}\textbf{v}\]

También podemos escribir la proyección de\(\textbf{u}\) onto\(\textbf{v}\) como

\[\textbf{proj}_\textbf{v}\textbf{u} = \dfrac{\textbf{u}\cdot \textbf{v}}{|\textbf{v}|^{2}}\textbf{v} = \dfrac{\textbf{u}\cdot \textbf{v}}{\textbf{v}\cdot \textbf{v}}\textbf{v}\]

El componente de viento que actúa perpendicular a la dirección de\(\textbf{v}\) en la Figura\(\PageIndex{5}\) se denomina proyección de\(\textbf{u}\) ortogonal a\(\textbf{v}\) y se denota\(\textbf{proj}_{\perp\textbf{v}}\textbf{u}\) como se muestra en la Figura 3.32. Ya que\(\textbf{u} = \textbf{proj}_{\perp\textbf{v}}\textbf{u} + \textbf{proj}_{\textbf{v}}\textbf{u}\), tenemos que

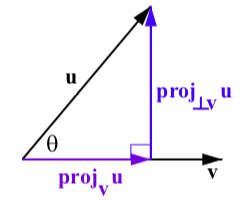
Figura\(\PageIndex{6}\): La\(\textbf{u}\) proyección de\(\textbf{v}\)

\[\textbf{proj}_{\perp\textbf{v}}\textbf{u} = \textbf{u} - \textbf{proj}_{\textbf{v}}\textbf{u}\]

A continuación se presenta un resumen de los resultados que hemos obtenido.

Para vectores distintos de cero\(\textbf{u}\) y\(\textbf{v}\), la proyección del vector\(\textbf{u}\) sobre el vector\(\textbf{v}\)\(\textbf{proj}_\textbf{v}\textbf{u}\), viene dada por

\[\textbf{proj}_\textbf{v}\textbf{u} = \dfrac{\textbf{u}\cdot \textbf{v}}{|\textbf{v}|^{2}}\textbf{v} = \dfrac{\textbf{u}\cdot \textbf{v}}{\textbf{v}\cdot \textbf{v}}\textbf{v}\]

Ver Figura\(\PageIndex{6}\). La proyección de\(\textbf{u}\) ortogonal a\(\textbf{v}\), denotada\(\textbf{proj}_{\perp\textbf{v}}\textbf{u}\), es

\[\textbf{proj}_{\perp\textbf{v}}\textbf{u} = \textbf{u} - \textbf{proj}_{\textbf{v}}\textbf{u}\]

Observamos que\[\textbf{u} = \textbf{proj}_{\perp\textbf{v}}\textbf{u} + \textbf{proj}_{\textbf{v}}\textbf{u}\]

Ejercicio\(\PageIndex{5}\)

Dejar\(\textbf{u} = \langle 7, 5 \rangle\) y\(\textbf{v} = \langle 10, -2\rangle\). Determinar\(\textbf{proj}_{\textbf{v}}\textbf{u}\) y\(\textbf{proj}_{\perp\textbf{v}}\textbf{u}\), y verificar eso\(\textbf{u} = \textbf{proj}_{\perp\textbf{v}}\textbf{u} + \textbf{proj}_{\textbf{v}}\textbf{u}\). Dibuja un cuadro que muestre todos los vectores involucrados en esto.

Contestar

Dejar\(\textbf{u} = \langle 7, 5 \rangle\) y\(\textbf{v} = \langle 10, -2\rangle\). Entonces

\[\textbf{proj}_{v}\textbf{u} = \dfrac{\textbf{u} \cdot \textbf{v}}{\textbf{|v|}^{2}}\textbf{v} = \langle \dfrac{600}{104}, \dfrac{-120}{104} \rangle \approx \langle 5.769, -1.154 \rangle\]
\[\textbf{proj}_{\perp\textbf{v}}\textbf{u} = \textbf{u} - \dfrac{\textbf{u} \cdot \textbf{v}}{\textbf{|v|}^{2}}\textbf{v}= \langle 7, 5 \rangle - \langle \dfrac{600}{104}, \dfrac{-120}{104} \rangle = \langle \dfrac{128}{104}, \dfrac{640}{104} \rangle \approx \langle 1.231, 6.154 \rangle\]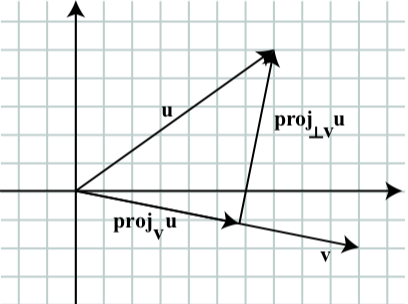

Resumen de la Sección 3.6

En esta sección, se estudiaron los siguientes conceptos e ideas importantes:

La forma componente de un vector\(\textbf{v}\) se escribe como\(\textbf{v} = \langle v_{1}, v_{2} \rangle\) y la\(\textbf{i},\textbf{j}\) forma del mismo vector es\(\textbf{v} = v_{1}\textbf{i} + v_{2}\textbf{j} \). Usando esta notación, tenemos

• La magnitud (o longitud) del vector\(\textbf{v}\) es\(\textbf{v} = \sqrt{v_{1}^{2} + v_{2}^{2}}\).
• El ángulo de dirección de\(\textbf{v}\) es\(\theta\)\(0^\circ \leq \theta < 360^\circ\), dónde y\[\cos(\theta) = \dfrac{v_{1}}{|\textbf{v}|}\] y\[\sin(\theta) = \dfrac{v_{2}}{|\textbf{v}|}\]
• La componente horizontal y componente y vertical del vector\(\textbf{v}\) y el ángulo de dirección\(\theta\) son\[v_{1} = |\textbf{v}|\cos(\theta)\] y\[v_{2} = |\textbf{v}|\sin(\theta)\]

Para dos vectores\(\textbf{v}\) y\(\textbf{w}\) con\(\textbf{v} = \langle v_{1}, v_{2} \rangle = v_{1}\textbf{i} + v_{2}\textbf{j}\)\(\textbf{w} = \langle w_{1}, w_{2} \rangle = w_{1}\textbf{i} + w_{2}\textbf{j}\) y y un escalar\(c\):

• \[\textbf{v} + \textbf{w} = \langle v_{1} + w_{1}, v_{2} + w_{2}\rangle = (v_{1} + w_{1})\textbf{i} + (v_{2} + w_{2})\textbf{j}\]
• \[\textbf{v} - \textbf{w} = \langle v_{1} - w_{1}, v_{2} - w_{2}\rangle = (v_{1} - w_{1})\textbf{i} + (v_{2} - w_{2})\textbf{j}\]
• \[c\textbf{v} = \langle cv_{1}, cv_{2}\rangle = (cv_{1})\textbf{i} + (cv_{2})\textbf{j}\]
• El producto de punto de\(\textbf{v}\) y\(\textbf{w}\) es\(\textbf{u}\cdot \textbf{v} = u_{1}v_{1} + u_{2}v_{2}.\)
• Si\(\theta\) es el ángulo entre\(\textbf{v}\) y\(\textbf{w}\), entonces\[\textbf{u} \cdot \textbf{u} = |\textbf{u}||\textbf{v}|\cos(\theta)\] o\[\cos(\theta) = \dfrac{\textbf{u}\cdot \textbf{v}}{|\textbf{u}||\textbf{v}|}\]
• La proyección del vector\(\textbf{v}\) sobre el vector\(\textbf{w}\)\(\textbf{proj}_\textbf{w}\textbf{v}\), viene dada por

  \[\textbf{proj}_\textbf{w}\textbf{v} = \dfrac{\textbf{v}\cdot \textbf{w}}{|\textbf{w}|^{2}}\textbf{w} = \dfrac{\textbf{v}\cdot \textbf{w}}{\textbf{w}\cdot \textbf{w}}\textbf{w}\]

  La proyección de\(\textbf{v}\) ortogonal a\(\textbf{w}\), denotada\(\textbf{proj}_{\perp\textbf{w}}\textbf{v}\), es
  \[\textbf{proj}_{\perp\textbf{w}}\textbf{v} = \textbf{v} - \textbf{proj}_{\textbf{w}}\textbf{v}\]

  Observamos que\[\textbf{w} = \textbf{proj}_{\perp\textbf{w}}\textbf{v} + \textbf{proj}_{\textbf{w}}\textbf{v}\] Ver Figura\(\PageIndex{7}\).

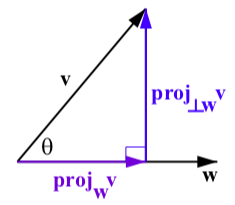
Figura\(\PageIndex{7}\): La\(\textbf{v}\) proyección de\(\textbf{w}\)