4.2: Ecuaciones Trigonométricas

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

• ¿Qué es una ecuación trigonométrica?
• ¿Qué significa resolver una ecuación trigonométrica?
• ¿En qué se diferencia una ecuación trigonométrica de una identidad trigonométrica?

Ya hemos aprendido a resolver ciertos tipos de ecuaciones trigonométricas. En la Sección 2.6 aprendimos a usar funciones trigonométricas inversas para resolver ecuaciones trigonométricas.

Actividad inicial

Refiérase al método de la Sección 2.6 para encontrar todas las soluciones a la ecuación\(\sin(x) = 0.4\).

Ecuaciones Trigonométricas

Cuando un rayo de luz de un punto se\(P\) refleja en una superficie en un punto\(R\) para iluminar un punto\(Q\) como se muestra a la izquierda en la Figura 4.1, la luz hace dos ángulos\(\alpha\) y\(\beta\) con una perpendicular a la superficie. El ángulo\(\alpha\) se llama ángulo de incidencia y el ángulo\(\beta\) se llama ángulo de reflexión. La Ley de Reflexión establece que cuando la luz se refleja en una superficie, el ángulo de incidencia es igual al ángulo de reflexión. ¿Qué sucede si la luz viaja a través de un medio (digamos aire) desde un punto\(P\), se desvía hacia otro medio (digamos agua) para viajar a un punto\(Q\)? Piensa en lo que sucede si miras un objeto en un vaso de agua. Ver Figura 4.1 a la derecha. Nuevamente la luz hace dos ángulos\(\alpha\) y\(\beta\) con una perpendicular a la superficie. El ángulo\(\alpha\) se llama ángulo de incidencia y el ángulo\(\beta\) se llama ángulo de refracción. Si la luz viaja del aire al agua, la Ley de Refracción dice que\[\dfrac{\sin(\alpha)}{\sin(\beta)} = \dfrac{c_{a}}{c_{w}}\]

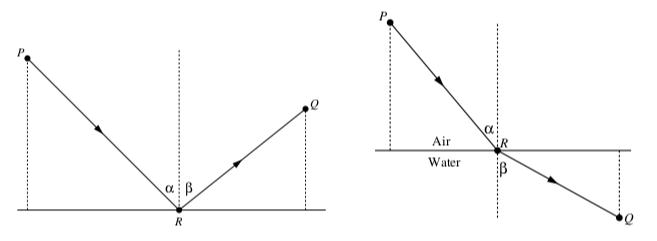
Figura\(\PageIndex{1}\): Reflexión y refracción.

donde\(c_{a}\) esta la velocidad de la luz en el aire y\(c_{w}\) es la velocidad de la luz en el agua. La relación entre\(\dfrac{c_{a}}{c_{w}}\) la velocidad de la luz en el aire y la velocidad de la luz en el agua se puede calcular por experimento. En la práctica, la velocidad de la luz en cada medio se compara con la velocidad de la luz en un vacío. La relación entre la velocidad de la luz en el vacío y la velocidad de la luz en el agua es de alrededor de 1.33. A esto se le llama el índice de refracción para el agua. El índice de refracción para el aire es muy cercano a 1, por lo que la relación\(\dfrac{c_{a}}{c_{w}}\) es cercana a 1.33. Normalmente podemos medir el ángulo de incidencia, por lo que la Ley de Refracción puede decirnos cuál es el ángulo de refracción resolviendo la ecuación (6).

Las ecuaciones trigonométricas surgen en una variedad de situaciones, como en la Ley de Refracción, y en una variedad de disciplinas que incluyen física, química e ingeniería. A medida que desarrollemos identidades trigonométricas en este capítulo, también las usaremos para resolver ecuaciones trigonométricas.

Recordemos que la Ecuación (6) es una ecuación condicional porque no es cierta para todos los valores permitidos de la variable. Resolver una ecuación condicional significa encontrar todos los valores para las variables que hacen que las dos expresiones a cada lado de la ecuación sean iguales entre sí.

Ecuaciones de Tipo Lineal

La sección 2.6 nos mostró cómo resolver ecuaciones trigonométricas que son reducibles a ecuaciones lineales. Revisamos esa idea en nuestro primer ejemplo.

Ejemplo\(\PageIndex{1}\): (Solving an Equation of Linear Type)

Considerar la ecuación\[2\sin(x) = 1.\]
Queremos encontrar todos los valores de\(x\) que satisfagan esta ecuación. Observe que esta ecuación se parece mucho a la ecuación lineal\(2y = 1\), con\(\sin(x)\) en lugar de\(y\). Entonces esta ecuación trigonométrica es de tipo lineal y decimos que es lineal en\(\sin(x)\). Sabemos resolver\(2y = 1\), simplemente dividimos ambos lados de la ecuación por 2 para obtener\(y = \dfrac{1}{2}\). Podemos aplicar la misma operación algebraica\(2\sin(x) = 1\) para obtener la ecuación\[\sin(x) = \dfrac{1}{2}.\]

Ahora podríamos proceder de un par de maneras. De trabajos anteriores sabemos que\(\sin(x) = \dfrac{1}{2}\) cuando\(x = \dfrac{\pi}{6}\). Alternativamente, podríamos aplicar el seno inverso a ambos lados de nuestra ecuación para ver que una solución es\(x = \sin^{-1}(\dfrac{1}{2}) = \dfrac{\pi}{6}\).

Recordemos, sin embargo, esta no es la única solución. La primera tarea es encontrar todas las soluciones en un periodo completo de la función sinusoidal. Podemos usar el intervalo con\(0 \leq x \leq 2\pi\) pero a menudo usamos el intervalo\(-\pi \leq x \leq \pi\). En este caso, no hace diferencia ya que la función sinusoidal es positiva en el segundo cuadrante. Usando\(\dfrac{\pi}{6}\) como ángulo de referencia, vemos que\(x = \pi - \dfrac{\pi}{6} = \dfrac{5\pi}{6}\) es otra solución de esta ecuación. (Use una calculadora para verificar esto).
Ahora usamos el hecho de que la función seno es punto con un periodo de\(2\pi\) para escribir fórmulas que puedan ser utilizadas para generar todas las soluciones de la ecuación\(2\sin(x) = 1\).

Entonces los ángulos en el primer cuadrante son\(\dfrac{\pi}{6} + k(2\pi)\). y los ángulos en el segundo cuadrante son\(\dfrac{5\pi}{6} + k(2\pi)\) donde\(k\) es un entero. Entonces para las soluciones de la ecuación\(2\sin(x) = 1\), escribimos\(x = \dfrac{\pi}{6} + k(2\pi)\) o\(x = \dfrac{5\pi}{6} + k(2\pi)\), donde\(k\) está un entero.

Siempre podemos verificar nuestras soluciones graficando ambos lados de la ecuación para ver dónde se cruzan las dos expresiones. La Figura 4.2 muestra que las gráficas de\(y = 2\sin(x)\) y\(y = 1\) sobre el intervalo\([-2\pi, 3\pi]\). Podemos ver que los puntos de intersección de estas dos curvas ocurren exactamente en las soluciones que encontramos para esta ecuación.

Ejercicio\(\PageIndex{1}\)

Encuentra los valores exactos de todas las soluciones a la ecuación\(4\cos(x) = 2\sqrt{2}\). Haga esto primero encontrando todas las soluciones en un período completo de la función coseno y

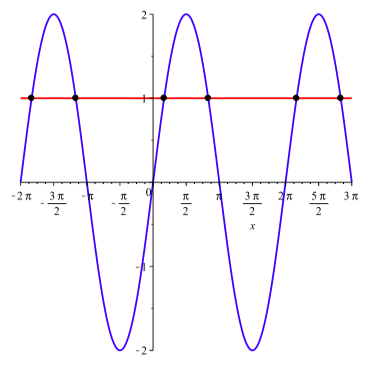
Figura\(\PageIndex{2}\): Las gráficas de\(y = 2\sin(x)\) y\(y = 1\)

luego usando la propiedad periódica para escribir fórmulas que se pueden usar para generar todas las soluciones de la ecuación. Dibuja gráficas apropiadas para ilustrar tus soluciones.

Contestar

Dividimos ambos lados de la ecuación\(4\cos(x) = 2\sqrt{2}\) para obtener\(\cos(x) = \dfrac{\sqrt{2}}{2}\). Entonces\[x = \dfrac{\pi}{4} + k(2\pi)\] o\[x = \dfrac{7\pi}{4} + k(2\pi)\]
donde\(k\) es un entero.

Resolver una ecuación usando una función inversa

Cuando resolvimos la ecuación\(2\sin(x) = 1\), usamos el hecho de que sabemos eso\(\sin(\dfrac{\pi}{6}) = \dfrac{1}{2}\). Cuando no podemos usar uno de los arcos comunes, utilizamos el método más general de usar una función trigonométrica inversa. Esto es lo que hicimos en la Sección 2.6. Consulte “Una estrategia para resolver una función trigonométrica” en la página 158. Ilustraremos esta estrategia con la ecuación\(\cos(x) = 0.7\). Comenzamos aplicando la función coseno inversa a ambos lados de esta ecuación para obtener

\[\cos(x) = 0.7\]
\[\cos^{-1}(\cos(x)) = \cos^{-1}(0.7)\]
\[x = \cos^{-1}(0.7)\]

Esto da la única solución para la ecuación que está en intervalo\([0, \pi]\). Antes de usar la propiedad periódica, necesitamos determinar las otras soluciones para la ecuación en un periodo completo de la función coseno. Podemos usar el intervalo\([0, 2\pi]\) pero es más fácil usar el intervalo\([-\pi, \pi]\). Una de las razones de ello es la siguiente llamada “identidad de arco negativo” señalada en la página 82.

\[\cos(-x) = \cos(x)\]por cada número real\(x\).

De ahí que ya que una solución para la ecuación es\(x = \cos^{-1}(0.7)\), otra solución lo es\(x = -\cos^{-1}(0.7)\). Esto quiere decir que las dos soluciones de la ecuación\[x = \cos(x)\] sobre el intervalo\([-\pi, \pi]\) son\(x = \cos^{-1}(0.7)\) y\(x = -\cos^{-1}(0.7)\)
Dado que el periodo ide la función coseno es\(2\pi\), podemos decir que cualquier solución de la ecuación\(\cos(x) = 0.7\) será de la forma\(x = \cos^{-1}(0.7) + k(2\pi)\) y\(x = -\cos^{-1}(0.7) + k(2\pi)\) donde \(k\)es algún número entero.

Nota

Nota: La actividad inicial para esta sección tuvo la ecuación\(\sin(x) = 0.4\). Las soluciones para esta ecuación son
\(x = \arcsin(0.4) + k(2\pi)\) y\(x = (\pi - \arcsin(0.4)) + k(2\pi)\) dónde\(k\) está algún número entero.

Podemos escribir las soluciones en forma aproximada como\(x = 0.41152 + k(2\pi)\) y\(x = 2.73008 + k(2\pi)\) donde\(k\) es un entero.

Ejercicio\(\PageIndex{2}\)

1. Determinar fórmulas que se pueden utilizar para generar todas las soluciones a la ecuación\(5\sin(x) = 2\). Dibuja gráficas apropiadas para ilustrar tus soluciones en un periodo de la función sinusoidal.
2. Aproximar, a dos decimales, el ángulo de refracción de la luz que pasa del aire al agua si el ángulo de incidencia es\(40^\circ\).

Contestar

1. Dividimos ambos lados de la ecuación\(5\sin(x) = 2\) por\(5\) para obtener\(\sin(x) = 0.4\).

Así\[x = \sin^{-1}(0.4) + k(2\pi)\] o\[x = (\pi - \sin^{-1}(0.4)) + k(2\pi)\]

donde\(k\) es un entero.
2. Utilizamos\(\alpha = 40^\circ\) y\(\dfrac{c_{a}}{c_{w}} = 1.33\) en la Ley de Refracción.

\[\dfrac{\sin(40^\circ)}{\sin(\beta)} = 1.33\]

\[\sin(\beta) = \dfrac{\sin(40^\circ)}{1.33} \approx 0.483299\]

\[\beta \approx 28.90^\circ\]

El ángulo de refracción es aproximadamente\(28.90^\circ\).

Resolver ecuaciones trigonométricas usando identidades

Podemos usar identidades trigonométricas conocidas para ayudarnos a resolver ciertos tipos de ecuaciones trigonométricas.

Ejemplo\(\PageIndex{1}\): (Using Identities to Solve Equations)

Considerar la ecuación trigonométrica\[\cos^{2}(x) - \sin^{2}(x) = 1\]

Esta ecuación se complica por el hecho de que hay dos funciones trigonométricas diferentes involucradas. En este caso utilizamos la Identidad Pitagórica\[\sin^{2}(x) + \cos^{2}(x) = 1\] resolviendo\(\cos^{2}(x)\) para obtener\[\cos^{2}(x) = 1- \sin^{2}(x).\]

Ahora podemos sustituir en la ecuación (7) para obtener

\[(1 - \sin^{2}(x)) - \sin^{2}(x) = 1\]
Tenga en cuenta que todo es en términos de solo la función sinusoidal y podemos proceder a resolver la ecuación desde aquí:\[(1 - \sin^{2}(x)) - \sin^{2}(x) = 1\]
\[1 - 2\sin^{2}(x) = 1\]
\[-2\sin^{2}(x) = 0\]
\[\sin^{2}(x) = 0\]
\[\sin(x) = 0\]
Sabemos que\(\sin(x) = 0\) cuando \(x = \pi k\)para cualquier entero\(k\), por lo que las soluciones a la ecuación\(\cos^{2}(x) - \sin^{2}(x) = 1\) son\(x = \pi k\) para cualquier entero\(k\).

Esto se ilustra mediante la Figura\(\PageIndex{3}\).

Ejercicio\(\PageIndex{3}\)

Encuentra los valores exactos de todas las soluciones a la ecuación\(\sin^{2}(x) = 3\cos^{2}(x)\). Dibuja gráficas apropiadas para ilustrar tus soluciones.

Contestar

Usaremos la identidad\(\cos^{2}(x) = 1 - \sin(x)\). Así que tenemos

\[\sin^{2}(x) = 3(1 - \sin^{2}(x))\]

\[\sin^{2}(x) = \dfrac{3}{4}\]

Entonces tenemos\(\sin(x) = \dfrac{\sqrt{3}}{2}\) o\(\sin(x) = -\dfrac{\sqrt{3}}{2}\). Para la primera ecuación, vemos que

\[x = \dfrac{\pi}{3} + 2\pi k\]o\[x = -\dfrac{\pi}{3} + 2\pi k\]

donde\(k\) es un entero, y para la segunda ecuación, tenemos

\[x = \dfrac{\pi}{3} + 2\pi k\]o\[x = \dfrac{\pi}{3} + 2\pi k\]

donde\(k\) es un entero. Las gráficas de\(y^{2} = \sin^{2}(x)\) y\(y^{2} = 3\cos^{2}(x)\) mostrarán\(4\) puntos de intersección en el intervalo\([0, 2\pi]\).

Otros métodos para resolver ecuaciones trigonométricas

Al igual que hicimos con las ecuaciones lineales, podemos ver algunas ecuaciones trigonométricas como de naturaleza cuadrática y usar herramientas del álgebra para resolverlas.

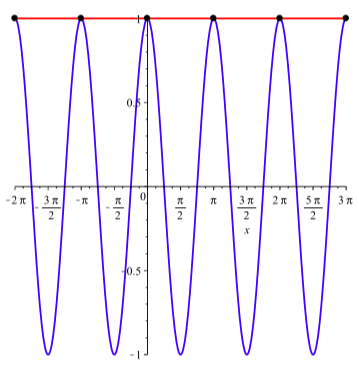
Figura\(\PageIndex{3}\): Las gráficas de\(y = \cos^{2}(x) - \sin^{2}(x)\) y\(y = 1\)

Ejemplo\(\PageIndex{2}\): (Solving Trigonometric Equations of Quadratic Type)

Considerar la ecuación trigonométrica\[\cos^{2}(x) - 2\cos(x) + 1 = 0\]

Esta ecuación parece una ecuación cuadrática familiar\(y^{2} - 2y + 1 = 0\). Podemos resolver esta ecuación cuadrática factorizando a obtener\((y - 1)^{2} = 0\). Así podemos aplicar la misma técnica a la ecuación trigonométrica\(\cos^{2}(x) - 2\cos(x) + 1 = 0\). Factorizar los rendimientos del lado izquierdo\[(\cos(x) - 1)^{2} = 0\]

La única manera que\((\cos(x) - 1)^{2} = 0\) puede ser 0 es si\((\cos(x) - 1)^{2}\) es 0. Esto reduce nuestra ecuación trigonométrica cuadrática a una ecuación trigonométrica lineal. Para resumir el proceso hasta el momento\[\cos^{2}(x) - 2\cos(x) + 1 = 0\]
\[(\cos(x) - 1)^{2} = 0\]
\[\cos(x) - 1 = 0\]
\[\cos(x) = 1\]
tenemos Sabemos que\(\cos(x) = 1\) cuando\(x = 2\pi k\) para valores enteros de\(k\). Por lo tanto, las soluciones a nuestra ecuación original son

\[x = 2\pi k\]

donde\(k\) es cualquier entero. A modo de comprobación, la gráfica de\(y = \cos^{2}(x) - 2\cos(x) + 1\) se muestra en la Figura\(\PageIndex{4}\). La figura parece mostrar que la gráfica de\(y = \cos^{2}(x) - 2\cos(x) + 1\) cruza el\(x\) eje -en exactamente los puntos que encontramos, por lo que nuestra solución es validada por medios gráficos.

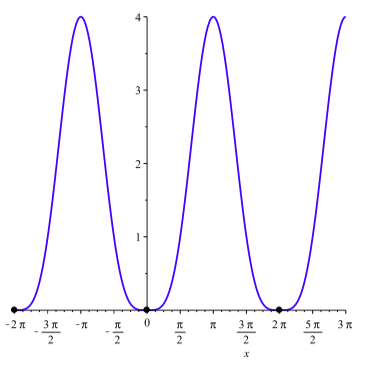
Figura\(\PageIndex{4}\): la gráfica de\(y = \cos^{2}(x) - 2\cos(x) + 1\)

Ejercicio\(\PageIndex{4}\)

Encuentra los valores exactos de todas las soluciones a la ecuación\(\sin^{2}(x - 4\sin(x) = -3)\). Dibuja gráficas apropiadas para ilustrar tus soluciones.

Contestar

Escribimos la ecuación como\(\sin(x) - 4\sin(x) + 3 = 0\) y factorizamos el lado derecho para obtener\((\sin(x) - 3)(\sin(x) - 1) = 0\). Entonces vemos eso\(\sin(x) - 3 = 0\) o\(\sin(x) - 1 = 0\). Sin embargo, la ecuación\(\sin(x) - 3 = 0\) es equivalente a\(\sin(x) = 3\), y esta ecuación no tiene solución. Escribimos\(\sin(x) - 1 = 0\) como\(\sin(x) = 1\) y así las soluciones son

\[x = \dfrac{\pi}{2} + 2\pi k\]

donde\(k\) es un entero.

Resumen

En esta sección, se estudiaron los siguientes conceptos e ideas importantes:

Una ecuación trigonométrica es una ecuación condicional que involucra funciones trigonométricas. Si es posible escribir la ecuación en la forma

\(\text{“some trigonometric function of } x \text{"} = \text{a number}\)

podemos usar la siguiente estrategia para resolver la ecuación:

• Encuentra todas las soluciones de la ecuación dentro de un periodo de la función. Esto a menudo se hace mediante el uso de propiedades de la función trigonométrica. Muy a menudo, habrá dos soluciones dentro de un solo periodo.
• Utilice el período de la función para expresar fórmulas para todas las soluciones agregando múltiplos enteros del período a cada solución encontrada en el primer paso. Por ejemplo, si la función tiene un periodo de\(2\pi\) y\(x_{1}\) y\(x_{2}\) son las dos únicas soluciones en un periodo completo, entonces escribiríamos las soluciones para la ecuación como\[x = x_{1} + k(2\pi), x = x_{2} + k(2\pi)\] donde\(k\) es un entero:

A veces podemos usar identidades trigonométricas para ayudar a reescribir una ecuación dada en forma de ecuación (1).