4.3: Suma y Diferencia de Identidades

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

• ¿Cuáles son las identidades de diferencia coseno y suma?
• ¿Cuáles son las identidades de diferencia sinusoidal y suma?
• ¿Cuáles son las identidades de diferencia tangente y suma?
• ¿Cuáles son las Identidades de Cofunción?
• ¿Por qué son útiles las identidades de diferencia y suma?

Las siguientes identidades que investigaremos son las identidades de suma y diferencia para el coseno y el seno. Estas identidades nos ayudarán a encontrar valores exactos para las funciones trigonométricas en muchos más ángulos y también proporcionarán un medio para derivar aún más identidades.

Actividad de inicio

1. ¿Es\(\cos(A - B) = \cos(A) - \cos(B)\) una identidad? Explique.
2. ¿Es\(\sin(A - B) = \sin(A) - \sin(B)\) una identidad? Explique.
3. Utilice una utilidad gráfica para dibujar la gráfica de\(y = \sin(\dfrac{\pi}{2} - x)\) y\(y = \cos(x)\) sobre el intervalo\([-2\pi, 2\pi]\) en el mismo conjunto de ejes. ¿Crees que\(y = \sin(\dfrac{\pi}{2} - x) = \cos(x)\) es una identidad? ¿Por qué o por qué no?

La identidad de la diferencia del coseno

A este punto conocemos los valores exactos de las funciones trigonométricas en solo unos pocos ángulos. Las identidades trigonométricas pueden ayudarnos a extender esta lista de ángulos en los que conocemos los valores exactos de las funciones trigonométricas. Consideremos, por ejemplo, el problema de encontrar el valor exacto de\(\cos(\dfrac{\pi}{12})\). Las definiciones e identidades que tenemos hasta ahora no nos ayudan con este problema. No obstante, podríamos notar eso\(\dfrac{\pi}{12} = \dfrac{\pi}{3} - \dfrac{\pi}{4}\) y si supiéramos cómo se comportaba el coseno con respecto a la diferencia de dos ángulos, entonces podríamos encontrar\(\cos(\dfrac{\pi}{12})\). En nuestra Actividad de Inicio, sin embargo, vimos que la ecuación no\(\cos(A - B) = \cos(A) - \cos(B)\) es una identidad, por lo que necesitamos entender cómo\(\cos(A - B)\) relacionarnos con cosenos y senos de\(A\) y\(B\).

A continuación señalamos la Identidad de Diferencia de Coseno. Esta identidad no es obvia, y se da una verificación de la identidad más adelante en este apartado. Por ahora nos enfocamos en usar la identidad.

Identidad de diferencia de coseno

Para cualquier número real\(A\) y\(B\) tenemos\[\cos(A - B) = \cos(A)\cos(B) + \sin(A)\sin(B)\]

Ejemplo\(\PageIndex{1}\): (Using the Cosine Difference Identity)

Volvamos a nuestro problema de encontrar\(\cos(\dfrac{\pi}{12})\). Como sabemos\(\dfrac{\pi}{12} = \dfrac{\pi}{3} - \dfrac{\pi}{4}\), podemos usar la Identidad de Diferencia de Coseno con\(A = \dfrac{\pi}{3}\) y\(B = \dfrac{\pi}{4}\) para obtener

\[\cos(\dfrac{\pi}{12}) = \cos(\dfrac{\pi}{3} - \dfrac{\pi}{4}) = \cos(\dfrac{\pi}{3})\cos(\dfrac{\pi}{4}) + \sin(\dfrac{\pi}{3}\sin(\dfrac{\pi}{4})) = (\dfrac{1}{2})(\dfrac{\sqrt{2}}{2}) + (\dfrac{\sqrt{3}}{2})(\dfrac{\sqrt{2}}{2}) = \dfrac{\sqrt{2}+\sqrt{6}}{4}.\]

Entonces vemos que\(\cos(\dfrac{\pi}{12}) = \dfrac{\sqrt{2}+\sqrt{6}}{4}.\)

Ejercicio\(\PageIndex{1}\)

1. Determinar el valor exacto de\(\cos(\dfrac{7\pi}{12})\) usar la Identidad de Diferencia de Coseno
2. Dado eso\(\dfrac{5\pi}{12} = \dfrac{\pi}{6} + \dfrac{\pi}{4} = \dfrac{\pi}{6} - (-\dfrac{\pi}{4})\), determinar el valor exacto de\(\cos(\dfrac{5\pi}{12})\) usar la Identidad de Diferencia de Coseno.

Contestar

1. Primero señalamos eso\(\dfrac{7\pi}{12} = \dfrac{9\pi}{12} - \dfrac{2\pi}{6} = \dfrac{3\pi}{4} - \dfrac{\pi}{6}\).

\[\cos(\dfrac{7\pi}{12}) = \cos(\dfrac{}{})\]

2.

\[\cos(\dfrac{5\pi}{12}) = \cos(\dfrac{\pi}{6} - (-\dfrac{\pi}{4})) = \cos(\dfrac{\pi}{6})\cos(\dfrac{\pi}{4}) + \sin(\dfrac{\pi}{6})\sin(-\dfrac{\pi}{4}) = (\dfrac{\sqrt{3}}{2})(\dfrac{\sqrt{2}}{2}) + (\dfrac{1}{2})(-\dfrac{\sqrt{2}}{2}) = \dfrac{\sqrt{6} - \sqrt{2}}{4}\]

La identidad de la suma coseno

Dado que existe una Identidad de Diferencia de Coseno, podríamos esperar que haya una Identidad de Suma Cosina. Podemos usar la Identidad de Diferencia Cosina junto con las identidades negativas para encontrar una identidad para\(\cos(A + B)\). La idea básica estaba contenida en nuestra última Comprobación de Progreso, donde escribimos\(A + B\) como\(A - (-B)\). Para ver cómo funciona esto en general, fíjese en que

\[\cos(A + B) = \cos(A - (-B)) = \cos(A)\cos(-B) + \sin(A)\sin(-B) = \cos(A)\cos(B) - \sin(A)\sin(B)\]

Esta es la Identidad de la Suma Cosina.

Identidad de suma coseno

Para cualquier número real\(A\) y\(B\) tenemos
\[\cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B)\]

Ejercicio\(\PageIndex{2}\)

1. Encuentre una fórmula más simple para\(\cos(\pi + x)\) en términos de\(\cos(x)\). Ilustrar con una gráfica.
2. Usa la Identidad de Diferencia de Coseno para probar que\(\cos(\dfrac{\pi}{2} - x) = \sin(x)\) es una identidad.

Contestar

1. \(\cos(\pi + x) = \cos(\pi)\cos(x) - \sin(\pi)\sin(x) = -\cos(x)\). Las gráficas de\(y = \cos(\pi + x)\) y\(y = \cos(x)\) son indenticales.
2. \(\cos(\dfrac{\pi}{2} - x) = \cos(\dfrac{\pi}{2})\cos(x) + \sin(\dfrac{\pi}{2})\sin(x) = 0\cdot \cos(x) + 1\cdot \sin(x)\). Entonces vemos que\(\cos(\dfrac{\pi}{2} - x) = \sin(x)\)

Identidades de cofunción

En Progress Check 4.14 utilizamos la Identidad de Diferencia de Coseno para ver que\(\cos(\dfrac{\pi}{2} - x) = \sin(x)\) es una identidad. Dado que esto es una identidad, podemos reemplazarlo\(x\) con\(\dfrac{\pi}{2} - x\) para ver que

\[\sin(\dfrac{\pi}{2} - x) = \cos(\dfrac{\pi}{2} - (\dfrac{\pi}{2} - x)) = \cos(x),\]

así\[\sin(\dfrac{\pi}{2} - x) = \cos(x),\]. Las dos identidades

\[\cos(\dfrac{\pi}{2} - x) = \sin(x)\]y\[\sin(\dfrac{\pi}{2} - x) = \cos(x)\]

se llaman identidades de cofunción. Estas dos identidades de cofunción muestran que el seno y el coseno de los ángulos agudos en un triángulo rectángulo están relacionados de una manera particular.

Dado que la suma de las medidas de los ángulos en un triángulo rectángulo es\(\pi\) radianes o\(180^\circ\), las medidas de los dos ángulos agudos en un triángulo rectángulo suman a\(\dfrac{\pi}{2}\) radianes o\(90^\circ\). Se dice que tales ángulos son complementarios. Así, el seno de un ángulo agudo en un triángulo rectángulo es el mismo que el coseno de su ángulo complementario. Por esta razón llamamos a las cofunciones seno y coseno. La denominación de las seis funciones trigonométricas refleja el hecho de que vienen en tres conjuntos de pares de cofunciones: el seno y el coseno, la tangente y la cotangente, y la secante y la cosecante. Las identidades de cofunción son las mismas para cualquier par de cofunción.

Identidades de cofunción

Para cualquier número real x para el que se definan las expresiones,

• \(\cos(\dfrac{\pi}{2} - x) = \sin(x)\)
• \(\sin(\dfrac{\pi}{2} - x) = \cos(x)\)
• \(\tan(\dfrac{\pi}{2} - x) = \cot(x)\)
• \(\cot(\dfrac{\pi}{2} - x) = \tan(x)\)
• \(\sec(\dfrac{\pi}{2} - x) = \csc(x)\)
• \(\csc(\dfrac{\pi}{2} - x) = \sec(x)\)

Para cualquier ángulo\(x\) en grados para el que se definan las funciones,

• \(\cos(90^\circ - x) = \sin(x)\)
• \(\sin(90^\circ - x) = \cos(x)\)
• \(\tan(90^\circ- x) = \cot(x)\)
• \(\cot(90^\circ - x) = \tan(x)\)
• \(\sec(90^\circ - x) = \csc(x)\)
• \(\csc(90^\circ - x) = \sec(x)\)

Ejercicio\(\PageIndex{3}\)

Utilizar las identidades de coseno y cofunción sinusoidal para probar la identidad de cofunción\[\tan(90^\circ- x) = \cot(x)\]

Contestar

Usaremos la identidad\(\tan(y) = \dfrac{\sin(y)}{\cos(y)}\).

\[\tan(\dfrac{\pi}{2} - x) = \dfrac{\sin(\dfrac{\pi}{2} - x)}{\cos(\dfrac{\pi}{2} - x)} = \dfrac{\cos(x)}{\sin(x)} = \cot(x)\]

La diferencia sinusoidal y las identidades de suma

Ahora podemos usar la Identidad de Diferencia de Coseno y las Identidades de Cofunción para derivar una Identidad de Diferencia Sinusal:

\[\sin(A - B) = \cos(\dfrac{\pi}{2} - (A - B)) = \cos((\dfrac{\pi}{2} - A) + B)) = \cos(\dfrac{\pi}{2} - A)\cos(B) - \sin(\dfrac{\pi}{2} - A)\sin(B)= \sin(A)\cos(B) - \cos(A)\sin(B).\]

Podemos derivar una identidad de suma sinusoidal a partir de la identidad de diferencia sinusoidal:

\[\sin(A + B) = \sin(A - (-B)) = \sin(A)\cos(-B) - \cos(A)\sin(-B) = \sin(A)\cos(B) + \cos(A)\sin(B)\]

Identidades de diferencia sinusoidal y suma

Para cualquier número real\(A\) y\(B\) tenemos
\[\sin(A - B) = \sin(A)\cos(B) - \cos(A)\sin(B)\] y\[\sin(A + B) = \sin(A)\cos(B) + \cos(A)\sin(B)\]

Ejercicio\(\PageIndex{4}\)

Utilice las identidades de suma sinusoidal o diferencia para encontrar los valores exactos de lo siguiente.

1. \[\sin(\dfrac{\pi}{12})\]
2. \[\sin(\dfrac{5\pi}{12})\]

Contestar

1. Tomamos nota de eso\(\dfrac{\pi}{12} = \dfrac{\pi}{3} - \dfrac{\pi}{4}\).

\[\sin(\dfrac{\pi}{12}) = \sin(\dfrac{\pi}{3} - \dfrac{\pi}{4}) = \sin(\dfrac{\pi}{3})\cos(\dfrac{\pi}{4}) - \cos(\dfrac{\pi}{3})\sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{3}}{2}\cdot \dfrac{\sqrt{2}}{2} - \dfrac{1}{2}\cdot \dfrac{\sqrt{2}}{2} = \dfrac{\sqrt{6} - \sqrt{2}}{4}\]

2. Tomamos nota de eso\(\dfrac{5\pi}{12} = \dfrac{\pi}{4} + \dfrac{\pi}{6}\).

\[\sin(\dfrac{5\pi}{12}) = \dfrac{\pi}{4} + \dfrac{\pi}{6} = \sin(\dfrac{\pi}{4})\cos(\dfrac{\pi}{6}) + \cos(\dfrac{\pi}{4})\sin(\dfrac{\pi}{6}) = \dfrac{\sqrt{2}}{2}\cdot \dfrac{\sqrt{3}}{2} + \dfrac{\sqrt{2}}{2}\cdot \dfrac{1}{2} = \dfrac{\sqrt{6} + \sqrt{2}}{4}\]

Uso de identidades de suma y diferencia para resolver ecuaciones

Como hemos hecho antes, podemos usar nuestras nuevas identidades para resolver otro tipo de ecuaciones trigonométricas.

Ejemplo\(\PageIndex{2}\): (Using the Cosine Sum Identity to Solve an Equation)

Considera la ecuación
\[\cos(\theta)\cos(\dfrac{\pi}{5}) - \sin(\theta)\sin(\dfrac{\pi}{5}) = \dfrac{\sqrt{3}}{2}\]

En la superficie esta ecuación parece bastante complicada, pero podemos aplicar una identidad para simplificarla hasta el punto en que sea sencillo de resolver. Observe que el lado izquierdo de esta ecuación tiene la forma\(\cos(A)\cos(B) - \sin(A)\sin(B)\) con\(A = \theta\) y\(B = \dfrac{\pi}{5}\)

Podemos usar la identidad de suma coseno\(\cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B)\) para combinar los términos de la izquierda en un solo término, y podemos resolver la ecuación a partir de ahí:

\[\cos(\theta)\cos(\dfrac{\pi}{5}) - \sin(\theta)\sin(\dfrac{\pi}{5}) = \dfrac{\sqrt{3}}{2}\]

\[\cos(\theta + \dfrac{\pi}{5}) = \dfrac{\sqrt{3}}{2}\]

Ahora\(\cos(x) =\dfrac{\sqrt{3}}{2}\) cuando\(x = \dfrac{\pi}{6} + 2k\pi\) o\(x = -\dfrac{\pi}{6} + 2k\pi\) para enteros\(k\). Así,\(\cos(\theta + \dfrac{\pi}{5}) = \dfrac{\sqrt{3}}{2}\) cuando\(\theta + \dfrac{\pi}{5} = \dfrac{\pi}{6} + 2k\pi\) o\(\theta + \dfrac{\pi}{5} = -\dfrac{\pi}{6} + 2k\pi\). Resolver para nos\(\theta\) da las soluciones

\[\theta = -\dfrac{\pi}{30} + 2k\pi\]o\[\theta = -\dfrac{11\pi}{30} + 2k\pi\]
donde\(k\) es cualquier número entero. Estas soluciones se ilustran en la Figura\(\PageIndex{1}\).

Nota

Hasta ahora, hemos estado usando la frase “Determinar fórmulas que se pueden utilizar para generar todas las soluciones de una ecuación dada”. Esta no es terminología estándar sino que se utilizó para recordarnos lo que tenemos que hacer para resolver una ecuación trigonométrica. Ahora simplemente diremos: “Determine todas las soluciones para la ecuación dada”. Cuando veamos esto, debemos darnos cuenta de que tenemos que determinar fórmulas que puedan ser utilizadas para generar todas las soluciones de una ecuación dada.

Ejercicio\(\PageIndex{5}\)

Determinar todas las soluciones de la ecuación
\[\sin(x)\cos(1) + \cos(x)\sin(1) = 0.2\]

Pista: Usa una identidad de suma o diferencia y usa la función sinusoidal inversa.

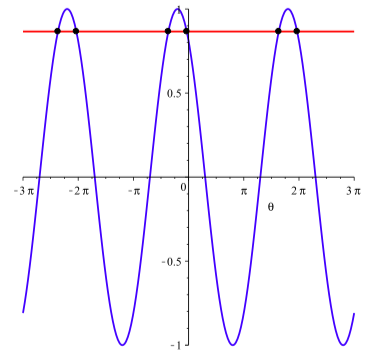
Figura\(\PageIndex{1}\): Gráficas de\(y = \cos(\theta)\cos(\dfrac{\pi}{5}) - \sin(\theta)\sin(\dfrac{\pi}{5})\) y\(y = \dfrac{\sqrt{3}}{2}\)

Contestar

Primero usamos la Identidad Sine Sum para reescribir la ecuación como\(\sin(x + 1) = 0.2\). Si lo dejamos\(t = x + 1\), lo vemos por\(0 \leq t < 2\pi\),

\[t = \arcsin(0.2)\]o\[t = (\pi - \arcsin(0.2))\]

Entonces tenemos\(x + 1 = \arcsin(0.2)\) o\(x + 1 = \pi - \arcsin(0.2)\). Ya que el periodo de las funciones con las que estamos trabajando es\(2\pi\), vemos que
\[x = (-1 + \arcsin(0.2)) + k(2\pi)\] o\[x = (-1 + \pi - \arcsin(0.2)) + k(2\pi)\]

donde\(k\) es un número entero.

Apéndice — Prueba de la Identidad de Diferencia de Coseno

Para entender cómo calcular el coseno de la diferencia de dos ángulos, dejar\(A\) y\(B\) ser ángulos arbitrarios en radianes. La Figura 4.7 muestra estos ángulos con\(A > B\), pero el argumento funciona en general. Si trazamos los puntos donde están los lados terminales de los ángulos\(A\),\(B\) e\(A - B\) intersectamos el círculo unitario, obtenemos la imagen en la Figura 4.7.

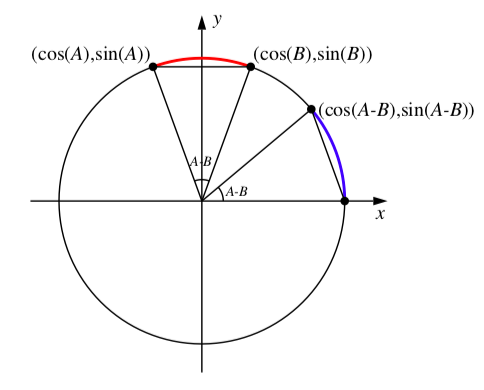
Figura\(\PageIndex{2}\): La fórmula de la diferencia de coseno

El arco en el círculo unitario desde el punto\((\cos(B), \sin(B))\) hasta el punto\((\cos(A), \sin(A))\) tiene longitud\(A - B\) y el arco del punto\((1, 0)\) al punto\((\cos(A - B), \sin(A - B))\) también tiene longitud\(A - B\). Entonces el acorde de\((\cos(B), \sin(B))\) a\((\cos(A), \sin(A))\) tiene la misma longitud que el acorde de (1,0) a\((\cos(A - B), \sin(A - B))\). Para encontrar la fórmula de diferencia de coseno, calculamos estas dos longitudes de cuerda usando la fórmula de distancia.

La longitud del acorde de\((\cos(B), \sin(B))\) a\((\cos(A), \sin(A))\) es

\[\sqrt{(\cos(A) - \cos(B))^{2} + (\sin(A) - \sin(B))^{2}}\]

y la longitud de la cuerda desde\((1, 0)\) el punto\((\cos(A - B), \sin(A - B))\) es

\[\sqrt{(\cos(A - B) - 1)^{2} + (\sin(A - B) - 0)^{2}}\]

Como estas dos longitudes de cuerda son las mismas obtenemos la ecuación

\[\sqrt{(\cos(A - B) - 1)^{2} + (\sin(A - B) - 0)^{2}} = \sqrt{(\cos(A) - \cos(B))^{2} + (\sin(A) - \sin(B))^{2}}\]

La identidad de diferencia de coseno se encuentra simplificando la Ecuación (2) al cuadrar primero ambos lados:

\[(\cos(A - B) - 1)^{2} + (\sin(A - B) - 0)^{2} = (\cos(A) - \cos(B))^{2} + (\sin(A) - \sin(B))^{2}\]

Luego expandimos ambos lados

\[[\cos^{2}(A - B) - 2\cos(A - B) + 1] + \sin^{2}(A - B) = [\cos^{2}(A) - 2\cos(A)\cos(B) + \cos^{2}(B)] + [\sin^{2}(A) - 2\sin(A)\sin(B) + \sin^{2}(B)]\]

Podemos combinar algunos términos similares:

\[[\cos^{2}(A - B) + \sin^{2}(A - B)] - 2\cos(A - B) + 1 = [\cos^{2}(A) + \sin^{2}(A)] + [\cos^{2}(B) + \sin^{2}(B)] - 2\sin(A)\sin(B) - 2\cos(A)\cos(B)]\]

Finalmente, el uso de las identidades pitagóreas produce

\[1 - 2\cos(A - B) + 1 = 1 + 1 - 2\cos(A)\cos(B) - 2\sin(A)\sin(B)\]
\[- 2\cos(A - B) = - 2\cos(A)\cos(B) - 2\sin(A)\sin(B)\]
\[\cos(A - B) = \cos(A)\cos(B) + \sin(A)\sin(B)\]

Resumen

En esta sección, se estudiaron los siguientes conceptos e ideas importantes:

• Identidades de suma y diferencia

  \[\cos(A - B) = \cos(A)\cos(B) + \sin(A)\sin(B)\]
  \[\cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B)\]
  \[\sin(A - B) = \sin(A)\cos(B) - \cos(A)\sin(B)\]
  \[\sin(A + B) = \sin(A)\cos(B) + \cos(A)\sin(B)\]

• Identidades de cofunción

Consulte la página 266 para obtener una lista de las identidades de cofunción.