4.4: Identidades de ángulo doble y medio

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

• ¿Cuáles son las identidades de doble ángulo para el seno, el coseno y la tangente?
• ¿Cuáles son las identidades de medio ángulo para el seno, el coseno y la tangente?
• ¿Cuáles son las identidades de producto a suma para el seno y el coseno?
• ¿Cuáles son las Identidades Suma a Producto para el seno y el coseno?
• ¿Por qué son útiles estas identidades?

Las identidades de suma y diferencia pueden ser utilizadas para derivar las identidades de ángulo doble y medio así como otras identidades, y veremos cómo en esta sección. Nuevamente, estas identidades nos permiten determinar valores exactos para las funciones trigonométricas en más puntos y también proporcionar herramientas para resolver ecuaciones trigonométricas (como veremos más adelante).

Actividad inicial

1. Utilizar\(B = A\) en la identidad de suma coseno\[\cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B)\] para escribir\(\cos(2A)\) en términos de\(\cos(A)\) y\(\sin(A)\).
2. ¿La ecuación es\[\dfrac{\cos(2x)}{2} = \cos(x)\] una identidad? Verifica tu respuesta.

Las identidades de doble ángulo

Supongamos que un tirador está disparando un arma con velocidad de hocico\(v_{0} = 1200\) pies por segundo a un objetivo a\(1000\) pies de distancia. Si descuidamos todas las fuerzas que actúan sobre la bala excepto la fuerza debida a la gravedad, la distancia horizontal que recorrerá la bala depende del ángulo\(\theta\) en el que se dispara el arma. Si dejamos\(r\) ser esta distancia horizontal (llamada el rango), entonces\[r = \dfrac{v_{0}^{2}}{g}\sin(2\theta),\]

donde\(g\) está la fuerza gravitacional que actúa para tirar de la bala hacia abajo. En este contexto,\(g = 32\) pies por segundo al cuadrado, dándonos

\[r = 45000\sin(2\theta)\]

El tirador querría saber el ángulo mínimo en el que debe disparar para golpear el objetivo a\(1000\) pies de distancia. Es decir, el tirador quiere determinar el ángulo para\(\theta\) que eso\(r = 1000\). Esto lleva a resolver la ecuación

\[45000\sin(2\theta) = 1000\]

Ecuaciones como la ecuación de rango en la que surgen con frecuencia múltiplos de ángulos, y en esta sección determinaremos fórmulas para\(\cos(2A)\) y\(\sin(2A)\) en términos de\(\cos(A)\) y\(\sin(A)\). Estas fórmulas se denominan identidades de doble ángulo. En nuestra Actividad de Inicio encontramos que

\[\cos(2A) = \cos^{2}(A) - \sin^{2}(A)\]
puede derivarse directamente de la identidad de suma coseno. Una identidad similar para el

sine se puede encontrar usando la Identidad Sine Sum:

\[\sin(2A) = \sin(A + A) = \sin(A)\cos(A) + \cos(A)\sin(A) = 2\cos(A)\sin(A).\]

Ejercicio\(\PageIndex{1}\)

Si\(\cos(\theta) = \dfrac{5}{13}\) y\(\dfrac{3\pi}{2} \leq \theta \leq 2\pi\), encontrar\(\cos(2\theta)\) y\(\sin(2\theta)\).

Contestar

Estamos asumiendo que\(\cos(\theta) = \dfrac{5}{13}\) y\(\dfrac{3\pi}{2} \leq \theta \leq 2\pi\). Para determinar\(\cos(2\theta)\) y\(\sin(2\theta)\), utilizaremos las indentidades de doble ángulo.
\[\cos(2\theta) = \cos^{2}(\theta) - \sin^{2}(\theta)\]

\[\sin(2\theta) = 2\cos(\theta)\sin(\theta)\]

Para usar estas identidades, también necesitamos saber\(\sin(\theta)\). Entonces usamos la identidad pitagórica.

\[\cos^{2}(\theta) + \sin^{2}(\theta) = 1\]

\[\sin^{2}(\theta) = 1 - \cos^{2}(\theta) = 1 - (\dfrac{5}{13})^{2} = \dfrac{144}{169}\]

Ya que\(\dfrac{3\pi}{2} \leq \theta \leq 2\pi\), vemos eso\(\sin(\theta) < 0\) y así\(\sin(\theta) = -\dfrac{12}{13}\). Por lo tanto,

\[\cos(2\theta) = \cos^{2}(\theta) - \sin^{2}(\theta) = (\dfrac{5}{13})^{2} - (-\dfrac{12}{13})^{2} = -\dfrac{119}{169}\]

\[\sin(2\theta) = 2\cos(\theta)\sin(\theta) = 2(\dfrac{5}{13})(-\dfrac{12}{13}) = -\dfrac{120}{169}\]

También hay una identidad de doble ángulo para la tangente. Dejamos la verificación de esa identidad para los ejercicios. Para resumir:

Identidades de doble ángulo

\[\cos(2A) = \cos^{2}(A) - \sin^{2}(A)\]

\[\sin(2A) = 2\cos(A)\sin(A)\]

\[\tan(2A) = \dfrac{2\tan(A)}{1 - \tan^{2}(A)}\]

Las dos primeras identidades son válidas para todos los números\(A\) y la tercera es válida siempre y cuando\(A \neq \dfrac{\pi}{4} + k(\dfrac{\pi}{2})\), donde\(k\) es un entero.

Ejercicio\(\PageIndex{2}\)

Demostrar las versiones alternas de la identidad de doble ángulo para el coseno.

1. \(\cos(2A) = 1 - 2\sin^{2}(A)\)
2. \(\cos(2A) = 2\cos^{2}(A) - 1\)

Contestar

Demostraremos formas alternas de la identidad de doble ángulo para coseno.

\[\cos(2A) = \cos^{2}(A) - \sin^{2}(A) = (1 - \sin^{2}(A)) - \sin^{2}(A) = 1 - \sin^{2}(A) - \sin^{2}(A) = 1 - 2\sin^{2}(A)\]

\[\cos(2A) = \cos^{2}(A) - \sin^{2}(A) = \cos^{2}(A) - (1 - \cos^{2}(A)) = \cos^{2}(A) - 1 + \cos^{2}(A) = 2\cos^{2}(A) - 1\]

Resolver ecuaciones con ángulos dobles

Resolver ecuaciones\(45000\sin(2\theta) = 1000\), como, que involucran múltiplos de ángulos, requiere el mismo tipo de técnicas que resolver otras ecuaciones, pero el ángulo múltiple puede agregar otra arruga.

Ejemplo\(\PageIndex{1}\): (Solving an Equation with a Multiple Angle)

Considera la ecuación\[2\cos(2\theta) - 1 = 0\]
Esta es una ecuación que es lineal en\(\cos(2\theta)\), por lo que podemos aplicar las mismas ideas que hicimos antes a esta ecuación. Resolvemos\(\cos(2\theta)\) para ver eso

\[\cos(2\theta) = \dfrac{1}{2}.\]

Conocemos los ángulos en los que el coseno tiene el valor\(\dfrac{1}{2}\), es decir,\(\dfrac{\pi}{3} + 2\pi k\) y\(-\dfrac{\pi}{3} + 2\pi k\) para los enteros\(k\). En nuestro caso, esta marca
\[2\theta = \dfrac{\pi}{3} + 2\pi k\] o\[2\theta = -\dfrac{\pi}{3} + 2\pi k\]
para enteros\(k\).

Ahora nos dividimos\(2\) para encontrar nuestras soluciones

\[\theta = \dfrac{\pi}{6} + \pi k\]o\[\theta = -\dfrac{\pi}{6} + \pi k\]

Estas soluciones se ilustran en la Figura\(\PageIndex{1}\).

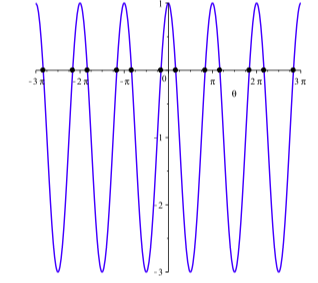
Figura\(\PageIndex{1}\): Gráficas de\(y = 2\cos(2\theta) - 1\).

Ejercicio\(\PageIndex{3}\)

Aproximar la solución positiva más pequeña en grados, a dos decimales, a la ecuación de rango

\[45000\sin(2\theta) = 1000\]

Contestar

Aproximaremos la solución positiva más pequeña en grados, a dos decimales, a la ecuación de rango
\[45000\sin(2\theta) = 1000\]

Dividiendo ambos lados de la ecuación por\(45000\), obtenemos\[\sin(2\theta) = \dfrac{1000}{45000} = \dfrac{1}{45}\]

Entonces\[2\theta = \arcsin(\dfrac{1}{45})\]

\[\theta = \dfrac{1}{2}\arcsin(\dfrac{1}{45})\]

Usando una calculadora en modo grados, obtenemos\(\theta \approx 0.64^\circ\).

También podemos usar las Identidades de Doble Ángulo para resolver ecuaciones con múltiples ángulos.

Ejemplo\(\PageIndex{2}\): (Solving an Equation with a Double Angle Identity)

Considera la ecuación

\[\sin(2\theta) = \sin(\theta)\]

El hecho de que las dos funciones trigonométricas tengan periodos diferentes hace que esta ecuación sea un poco más difícil. Podemos usar la Identidad de Doble Ángulo para el seno para reescribir la ecuación como

\[2\sin(\theta)\cos(\theta) = \sin(\theta)\]

En este punto podemos estar tentados a cancelar el factor de\(\sin(\theta)\) desde ambos lados, pero debemos resistir esa tentación porque\(\sin(\theta)\) puede ser 0 y no podemos dividir por 0. En cambio, pongamos todo un lado y factor:

\[2\sin(\theta)\cos(\theta) = \sin(\theta)\]

\[2\sin(\theta)\cos(\theta) - \sin(\theta) = 0\]

\[\sin(\theta)(2\cos(\theta) - 1) = 0\]

Ahora tenemos un producto que es igual a 0, por lo que al menos uno de los factores debe ser 0. Esto produce las dos ecuaciones

\[\sin(\theta) = 0\]o\[\cos(\theta) - 1 = 0\]

Resolvemos cada ecuación a su vez. Sabemos que\(\sin(\theta) = 0\) cuando\(\theta = \pi k\) para enteros\(k\). También,\(\cos(\theta) - 1 = 0\) implica\(\cos(\theta) = 1\), y esto sucede cuando\(\theta = 2\pi k\) para enteros\(k\).

Observe que estas soluciones son un subconjunto de la colección\(\pi k\) de soluciones de\(\sin(\theta) = 0\). Así, las soluciones a\(\sin(2\theta) = \sin(\theta)\) son\(\theta = \pi k\) para números enteros\(k\), como se ilustra en la Figura 4.10.

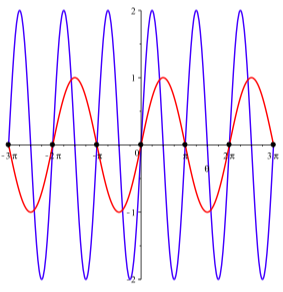
Figura\(\PageIndex{2}\): Gráficas de\(y = \sin(2\theta)\) y\(y = \sin(\theta)\)

Ejercicio\(\PageIndex{4}\)

El objetivo es resolver la ecuación\(\cos(2\theta) = \sin(\theta)\).

1. Usar una identidad de ángulo doble para ayudar a reescribir la ecuación en el formulario\[2\sin^{2}(\theta) + \sin(\theta) - 1 = 0\]
2. Resuelve la ecuación de tipo cuadrático en (1) factorizando el lado izquierdo de la ecuación.

Contestar

1. Utilizamos la identidad de doble ángulo\(\cos(2\theta) = 1 - 2\sin^{2}(\theta)\) para obtener

\[1 - 2\sin^{2}(\theta) = \sin(\theta)\]

\[1 - 2\sin^{2}(\theta) - \sin(\theta) = 0\]

\[2\sin^{2}(\theta) + \sin(\theta) - 1 = 0\]

2. Factoring da\(2(\sin(\theta) - 1)(\sin(\theta) + 1) = 0\). Estableciendo cada factor igual a\(0\) y resolviendo para\(\sin(\theta)\), obtenemos

\[\sin(\theta) = \dfrac{1}{2}\]o\[\sin(\theta) = -1\]

Así que tenemos

\[\theta = \dfrac{\pi}{6} + k(2\pi)\]o\[\theta = \dfrac{5\pi}{6} + k(2\pi)\] o\[\theta = -\pi + k(2\pi)\]

donde\(k\) es un entero.

Identidades de medio ángulo

Ahora investigamos las identidades de medio ángulo, identidades para\(\cos(\dfrac{A}{2})\) y\(\sin(\dfrac{A}{2})\).

Aquí utilizamos las identidades de doble ángulo de Ejercicio\(\PageIndex{4}\):

\[\cos(A) = \cos(2(\dfrac{A}{2}))\]

\[\cos(A) = 2\cos^{2}(\dfrac{A}{2}) - 1\]
\[\cos(A) + 1 = 2\cos^{2}(\dfrac{A}{2})\]
\[\cos^{2}(\dfrac{A}{2}) = \dfrac{\cos(A) + 1}{2}\]
\[\cos(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 + \cos(A)}{2}}\]

El signo de\(\cos(\dfrac{A}{2})\) depende del cuadrante en el que\(\dfrac{A}{2}\) yace.

Ejemplo\(\PageIndex{3}\): (Using the Cosine Half Angle Identity)

Podemos usar la Identidad de Medio Ángulo Cosino para determinar el valor exacto de\(\cos(\dfrac{7\pi}{12})\).

Si lo dejamos\(A = \dfrac{7\pi}{6}\), entonces tenemos\(\dfrac{7\pi}{12} = \dfrac{A}{2}\). La identidad de medio ángulo coseno nos muestra que

\[\cos(\dfrac{7\pi}{12}) = \cos(\dfrac{\dfrac{7\pi}{6}}{2}) = \pm\sqrt{\dfrac{1 + \cos(\dfrac{7\pi}{6})}{2}} = \pm\sqrt{\dfrac{1 - \dfrac{\sqrt{3}}{2}}{2}} = \pm\sqrt{\dfrac{2 - \sqrt{3}}{4}}\]

Dado que el lado terminal del ángulo\(\dfrac{7\pi}{12}\) se encuentra en el segundo cuadrante, sabemos que\(\cos(\dfrac{7\pi}{12})\) es negativo. Por lo tanto,

\[\cos(\dfrac{7\pi}{12}) = -\sqrt{\dfrac{2 - \sqrt{3}}{4}}.\]

Podemos encontrar una fórmula similar de medio ángulo para el seno usando el mismo enfoque:

\[\cos(A) = \cos(2(\dfrac{A}{2}))\]

\[\cos(A) = 1 - 2\sin^{2}(\dfrac{A}{2})\]
\[\cos(A) - 1 = 2\sin^{2}(\dfrac{A}{2})\]
\[\sin^{2}(\dfrac{A}{2}) = \dfrac{1 - \cos(A)}{2}\]
\[\sin(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 - \cos(A)}{2}}\]

Nuevamente, el signo de\(\sin(\dfrac{A}{2})\) depende del cuadrante en el que\(A\) yace.

Identidades de medio ángulo

Para resumir,

Para cualquier número\(A\) tenemos

\[\cos(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 + \cos(A)}{2}}\]

\[\sin(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 - \cos(A)}{2}}\]

donde el signo depende del cuadrante en el que\(\dfrac{A}{2}\) se encuentra.

Ejercicio\(\PageIndex{5}\)

Use una Identidad de Medio Ángulo para encontrar el valor exacto de\(\cos(\dfrac{\pi}{8})\).

Contestar

Para determinar el valor exacto de\(\cos(\dfrac{\pi}{8})\), utilizamos la Identidad de Medio Ángulo para coseno con\(A = \dfrac{\pi}{4}\).

\[\cos(\dfrac{\pi}{8}) = \pm\sqrt{\dfrac{1 + \cos(\dfrac{\pi}{4})}{2}} = \pm\sqrt{\dfrac{1 + \dfrac{\sqrt{2}}{2}}{2}}\]

Ya que\(\dfrac{\pi}{8}\) está en el primer cuadrante, usaremos la raíz cuadrada positiva. También podemos reescribir la expresión bajo el signo de raíz cuadrada para obtener

\[\cos(\dfrac{\pi}{8}) =\sqrt{\dfrac{1 + \dfrac{\sqrt{2}}{2}}{2}} = \sqrt{\dfrac{\dfrac{2 + \sqrt{2}}{2}}{2}} = \sqrt{\dfrac{2 + \sqrt{2}}{4}} = \dfrac{\sqrt{2 + \sqrt{2}}}{2}\]

Este resultado se puede verificar usando una calculadora.

Resumen

En esta sección, se estudiaron los siguientes conceptos e ideas importantes:

Identidades de doble ángulo

\[\cos(2A) = \cos^{2}(A) - \sin^{2}(A)\]
\[\cos(2A) = 2\cos^{2}(A) - 1\]
\[\cos(2A) = 1 - 2\sin^{2}(A)\]
\[\sin(2A) = 2\cos(A)\sin(A)\]
\[\tan(2A) = \dfrac{2\tan(A)}{1 - \tan^{2}(A)}\]

Identidades de medio ángulo

\[\cos(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 + \cos(A)}{2}}\]

\[\sin(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 - \cos(A)}{2}}\]

donde el signo depende del cuadrante en el que\(\dfrac{A}{2}\) se encuentra.