4.5: Identidades de suma-producto

Preguntas de enfoque

Las siguientes preguntas están destinadas a orientar nuestro estudio del material en esta sección. Después de estudiar esta sección, debemos entender los conceptos motivados por estas preguntas y poder escribir respuestas precisas y coherentes a estas preguntas.

• ¿Cuáles son las identidades de producto a suma para el seno y el coseno?
• ¿Cuáles son las Identidades Suma a Producto para el seno y el coseno?
• ¿Por qué son útiles estas identidades?

En general, las ecuaciones trigonométricas son muy difíciles de resolver con exactitud. Hemos estado usando identidades para resolver ecuaciones trigonométricas, pero todavía hay muchas más para las que no podemos encontrar soluciones exactas. Consideremos, por ejemplo, la ecuación

\[\sin(3x) + \sin(x) = 0\]

La gráfica de\(y = \sin(3x) + \sin(x)\) se muestra en la Figura\(\PageIndex{1}\). Podemos ver que hay muchas soluciones, pero las identidades que tenemos hasta ahora no nos ayudan con esta ecuación. Lo que haría que esta ecuación fuera más fácil de resolver es si pudiéramos reescribir la suma de la izquierda como producto — entonces podríamos usar el hecho de que un producto es cero si y solo si uno de sus factores es 0. Posteriormente presentaremos las Identidades Suma a Producto que nos ayudarán a resolver esta ecuación.

Actividad de inicio

Dejar\(A = 30^\circ\) y\(B = 45^\circ\). Calcular

\[\cos(A)\cos(B)\space and \space (\dfrac{1}{2})[\cos(A + B) + \cos(A - B)]\]

¿Qué notas?

Identidades de producto a suma

La suma coseno y las identidades de diferencia

\[\cos(A - B) = \cos(A)\cos(B) + \sin(A)\sin(B)\]

\[\cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B)\]

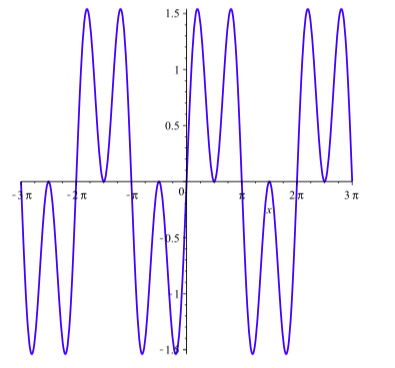
Figura\(\PageIndex{1}\): Gráfica de\(y = \sin(3x) + \sin(x)\).

nos permitirá desarrollar identidades que expresarán producto de cosenos o senos en términos de sumas de cosenos y senos. Para ver cómo surgen estas identidades, agregamos los lados izquierdo y derecho de (4) y (5) para obtener

\[\cos(A - B) + \cos(A + B) = 2\cos(A)\cos(B)\]

Entonces

\[\cos(A)\cos(B) = (\dfrac{1}{2})[\cos(A + B) + \cos(A - B)]\]

Del mismo modo, restar los lados izquierdo y derecho de (5) de (4) nos da

\[\cos(A - B) - \cos(A + B) = 2\sin(A)\cos(B)\]

Entonces

\[\sin(A)\sin(B) = (\dfrac{1}{2})[\cos(A - B) - \cos(A + B)]\]

De manera similar podemos obtener una fórmula para\(\cos(A)\cos(B)\). En este caso utilizamos las fórmulas de suma sinusoidal y diferencia

\[\sin(A - B) = \sin(A)\cos(B) - \cos(A)\sin(B)\]

\[\sin(A + B) = \sin(A)\cos(B) + \cos(A)\sin(B)\]

Sumando los lados izquierdo y derecho de (6) y (7) rendimientos

\[\sin(A - B) + \sin(A + B) = 2\sin(A)\cos(B)\]

Entonces

\[\sin(A)\cos(B) = (\dfrac{1}{2})[\sin(A + B) + \sin(A - B)]\]

Identidades de producto a suma

Para cualquier número\(A\) y\(B\) tenemos

\[\cos(A)\cos(B) = (\dfrac{1}{2})[\cos(A + B) + \cos(A - B)]\]

\[\sin(A)\sin(B) = (\dfrac{1}{2})[\cos(A - B) - \cos(A + B)]\]

\[\sin(A)\cos(B) = (\dfrac{1}{2})[\sin(A + B) + \sin(A - B)]\]

Ejercicio\(\PageIndex{1}\)

Encuentra el valor exacto de\(\sin(52.5^\circ)\sin(7.5^\circ)\).

Contestar

Para determinar el valor exacto de\(\sin(52.5^\circ)\sin(7.5^\circ)\), utilizaremos la identidad Producto-to-Suma

\[\sin(A)\sin(B) = (\dfrac{1}{2})[\cos(A - B) - \cos(A + B)]\]

Entonces vemos que
\[\sin(52.5^\circ)\sin(7.5^\circ) = (\dfrac{1}{2})[\cos(45^\circ) - \cos(60^\circ)] = (\dfrac{1}{2})[\dfrac{\sqrt{2}}{2} - \dfrac{1}{2}] = \dfrac{\sqrt{2} - 1}{4}\]

Identidades Suma a Producto

Como nuestras identidades finales, derivamos el reverso de las identidades de producto a suma. Estas identidades se denominan identidades SUM-a-producto. Por ejemplo, para verificar la identidad

\[\cos(A) + \cos(B) = 2\cos(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

primero señalamos que\(A = \dfrac{A + B }{2}\) y\(B = \dfrac{A + B}{2} - \dfrac{A - B}{2}\). Entonces

\[\cos(A) = \cos(\dfrac{A + B}{2} + \dfrac{A - B}{2}) = \cos(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2}) - \sin(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]
y

\[\cos(B) = \cos(\dfrac{A + B}{2} + \dfrac{A - B}{2}) = \cos(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2}) + \sin(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]

Agregar los lados izquierdo y derecho de (8) y (9) da como resultado

\[\cos(A) + \cos(B) = 2\cos(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

Además, si restamos los lados izquierdo y derecho de (9) de (8) obtenemos

\[\cos(A) - \cos(B) = -2\sin(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]

Del mismo modo,

\[\sin(A) = \sin(\dfrac{A + B}{2} + \dfrac{A - B}{2}) = \sin(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2}) + \cos(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]
y

\[\sin(B) = \sin(\dfrac{A + B}{2} + \dfrac{A - B}{2}) = \sin(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2}) - \cos(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]

Agregar los lados izquierdo y derecho de (10) y (11) da como resultado

\[\sin(A) + \sin(B) = 2\sin(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

Nuevamente, si restamos los lados izquierdo y derecho de (11) de (10) obtenemos

\[\sin(A) - \sin(B) = 2\cos(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]

Identidades Suma a Producto

Para cualquier número\(A\) y\(B\) tenemos

\[\cos(A) + \cos(B) = 2\cos(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

\[\cos(A) - \cos(B) = -2\sin(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]

\[\sin(A) + \sin(B) = 2\sin(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

\[\sin(A) - \sin(B) = 2\cos(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]

Ejercicio\(\PageIndex{2}\)

Encuentra el valor exacto de\(\cos(112.5^\circ) + \cos(67.5^\circ)\).

Contestar

Para determinar el valor exacto de\(\cos(112.5^\circ) + \cos(67.5^\circ)\), utilizaremos la identidad de SUM a producto

\[\cos(A) + \cos(B) = 2\cos(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

Entonces vemos que

\[\cos(112.5^\circ) + \cos(67.5^\circ) = 2\cos(\dfrac{180^\circ}{2})\cos(\dfrac{45^\circ}{2}) = \cos(90^\circ)\cos(22.5^\circ) = 0\cdot\cos(22.5^\circ) = 0\]

Podemos usar estas identidades Suma a producto y de producto a suma para resolver aún más tipos de ecuaciones trigonométricas.

Ejemplo\(\PageIndex{1}\): (Solving Equations Using the Sum-to-Product Identity)

Volvamos al problema planteado al inicio de esta sección para resolver la ecuación

\[\sin(3x) + \sin(x) = 0\]

Uso de Suma a Producto

\[\sin(A) + \sin(B) = 2\sin(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

podemos reescribir la ecuación de la siguiente manera:

\[\sin(3x) + \sin(x) = 0\]

\[2\sin(\dfrac{4x}{2})\cos(\dfrac{x}{2}) = 0\]

\[2\sin(2x)\cos(\dfrac{x}{2}) = 0\]

La ventaja de esta forma es que ahora tenemos un producto de funciones iguales a\(0\), y la única manera en que un producto puede igualar\(0\) es si uno de los factores lo es\(0\). Esto reduce nuestro problema original a dos ecuaciones que podemos resolver:

\[\sin(2x) = 0\]o\[\cos(\dfrac{x}{2}) = 0\]

Sabemos que\(\sin(2x) = 0\) cuando\(2x = k\pi\) o\(x = k\dfrac{\pi}{2}\), donde\(k\) es cualquier entero, y\(\cos(\dfrac{x}{2}) = 0\) cuando\(\dfrac{x}{2} = \dfrac{\pi}{2} + k\pi\) o\(x = \pi + k2\pi\), donde\(k\) es cualquier entero. Estas soluciones se pueden ver donde la gráfica de\(y = \sin(3x) + \sin(x)\) cruza el\(x\) eje -como se ilustra en la Figura\(\PageIndex{2}\).

Resumen de Trigonometric Identity

Las identidades trigonométricas son útiles porque nos permiten determinar valores exactos para las funciones trigonométricas en más puntos que antes y también proporcionan herramientas para derivar nuevas identidades y para resolver ecuaciones trigonométricas. Aquí proporcionamos un resumen de nuestras identidades trigonométricas.

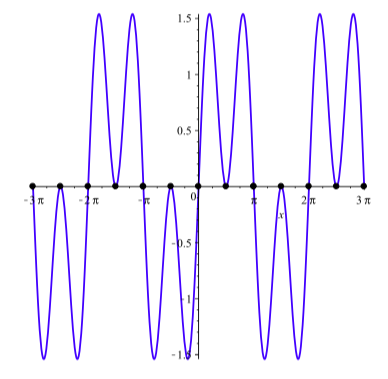
Figura\(\PageIndex{2}\): Gráfica de\(y = \sin(3x) + \sin(x)\).

Identidades de cofunción

\[\cos(\dfrac{\pi}{2} - A) = \sin(A)\]
\[\sin(\dfrac{\pi}{2} - A) = \cos(A)\]
\[\tan(\dfrac{\pi}{2} - A) = \cot(A)\]

Identidades de medio ángulo

\[\cos^{2}(\dfrac{A}{2}) = \dfrac{1 + \cos(A)}{2}\]
\[\cos(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 + \cos(A)}{2}}\]
\[\sin^{2}(\dfrac{A}{2}) = \dfrac{1 - \cos(A)}{2}\]
\[\sin(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 - \cos(A)}{2}}\]
\[\tan(\dfrac{A}{2}) = \sqrt{\dfrac{\sin(A)}{1 + \cos(A)}}\]
\[\tan(\dfrac{A}{2}) = \sqrt{\dfrac{1 - \cos(A)}{\sin(A)}}\]

Los signos de\(\cos(\dfrac{A}{2}\) y\(\sin(\dfrac{A}{2}\) dependen del cuadrante en el que\(\dfrac{A}{2}\) se encuentra.

Identidades de doble ángulo

\[\sin(2A) = 2\cos(A)\sin(A)\]
\[\cos(2A) = \cos^{2}(A) - \sin^{2}(A)\]
\[\cos(2A) = 1 - 2\sin^{2}(A)\]
\[\cos(2A) = 2\cos^{2}(A) - 1\]
\[\tan(2A) = \dfrac{2\tan(A)}{1 - \tan^{2}(A)}\]

Diferencia de coseno e identidades de suma

\[\cos(A) - \cos(B) = \cos(A)\cos(B) + \sin(A)\sin(B)\]

\[\cos(A) + \cos(B) = \cos(A)\cos(B) - \sin(A)\sin(B)\]

Identidades de diferencia sinusoidal y suma

\[\sin(A - B) = \sin(A)\cos(B) - \cos(A)\sin(B)\]

\[\sin(A + B) = \sin(A)\cos(B) + \cos(A)\sin(B)\]

Diferencia tangente e identidades de suma

\[\tan(A - B) = \dfrac{\tan(A) - \tan(B)}{1 + \tan(A)\tan(B)}\]
\[\tan(A + B) = \dfrac{\tan(A) + \tan(B)}{1 - \tan(A)\tan(B)}\]

Identidades de producto a suma

\[\cos(A)\cos(B) = (\dfrac{1}{2})[\cos(A + B) + \cos(A - B)]\]

\[\sin(A)\sin(B) = (\dfrac{1}{2})[\cos(A - B) - \cos(A - B)]\]

\[\sin(A)\cos(B) = (\dfrac{1}{2})[\sin(A + B) + \sin(A - B)]\]

Identidades Suma a Producto

\[\cos(A) + \cos(B) = 2\cos(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

\[\cos(A) - \cos(B) = -2\sin(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]

\[\sin(A) + \sin(B) = 2\sin(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

\[\sin(A) - \sin(B) = 2\cos(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]