4.E: Identidades y Ecuaciones Trigonométricas (Ejercicios)

Ejercicio\(\PageIndex{1}\)

Utilice una utilidad gráfica para graficar cada lado de la ecuación dada. Si la ecuación parece ser una identidad, probar la identidad. Si la ecuación parece no ser una identidad, demuestre una entrada en la que los dos lados de la ecuación tengan valores diferentes. Recuerde que al probar una identidad, trabaje para transformar un lado de la ecuación en el otro usando identidades conocidas. Algunos lineamientos generales son

1. Empezar por el lado más complicado.
2. A menudo es útil usar las definiciones para reescribir todas las funciones trigonométricas en términos de coseno y seno.
3. Cuando corresponda, factive o combine términos. Por ejemplo, se\(\sin^{2}(x) + \sin(x)\) puede escribir como\(\sin(x)(\sin(x) + 1)\) y se\(\dfrac{1}{\sin(x)} + \dfrac{1}{\cos(x)}\) puede escribir como la fracción única\(\dfrac{\cos(x) + \sin(x)}{\sin(x)\cos(x)}\) con un denominador común.
4. A medida que transforma un lado de la ecuación, tenga en cuenta el otro lado de la ecuación y use identidades que involucren términos que estén en el otro lado. Por ejemplo, para verificar eso\(\tan^{2}(x) + 1 = \dfrac{1}{\cos^{2}(x)}\), empezar\(\tan^{2}(x) + 1\) y hacer uso de identidades que se\(\tan(x)\) relacionen lo más estrechamente\(\cos(x)\) posible.

\[\cos(x)\tan(x) = \sin(x)\]

\[\dfrac{\cot(s)}{\csc(s)} = \cos(s)\]

\[\dfrac{\tan(s)}{\sec(s)} = \sin(s)\]

\[\cos^{2}(x) + 1 = \csc^{2}(x)\]

\[\sec^{2}(x) + \csc^{2}(x) = 1\]

\[\cot(t) + 1 = \csc(t)(\cos(t) + \sin(t))\]

\[\tan^{2}(\theta)(1 + \cot^{2}(\theta)) = \dfrac{1}{1 - \sin^{2}(\theta)}\]

\[\dfrac{1 - \sin^{2}(\beta)}{\cos(\beta)} = \sin(\beta)\]

\[\dfrac{1 - \sin^{2}(\beta)}{\cos(\beta)} = \cos(\beta)\]

\[\sin^{2}(x) + \tan^{2}(x) + \cos^{2}(x) = \sec^{2}(x)\]

Contestar

(a)\(\cos(x)\tan(x) = \cos(x)\dfrac{\sin(x)}{\cos(x)} = \sin(x)\)

b)\(\dfrac{\cot(x)}{(x)} = \dfrac{\dfrac{\cos(x)}{\sin(x)}}{\dfrac{1}{\sin(x)}} = \dfrac{\cos(x)}{\sin(x)} \times \dfrac{\sin{x}}{1} = \cos(x)\)

e) Una gráfica mostrará que no se trata de una identidad. En particular, vemos que\[\sec^{2}(\dfrac{\pi}{4}) + \csc^{2}(\dfrac{\pi}{4}) = (\sqrt{2})^{2} + (\sqrt{2})^{2} = 4\]

Ejercicio\(\PageIndex{2}\)

Un alumno afirma que\(\cos(\theta) + \sin(\theta) = 1\) es una identidad porque\(\cos(0) + \sin(0) = 1 + 0 = 0\). ¿Cómo le respondería a este alumno?

Ejercicio\(\PageIndex{3}\)

Si una ecuación trigonométrica tiene una solución, entonces la periodicidad de las funciones trigonométricas implica que la ecuación tendrá infinitamente muchas soluciones. Supongamos que tenemos una ecuación trigonométrica para la cual ambos lados de la ecuación son iguales en infinitamente muchas entradas diferentes. ¿La ecuación debe ser una identidad? Explica tu razonamiento

Ejercicio\(\PageIndex{4}\)

Para cada una de las siguientes ecuaciones, determinar fórmulas que pueden ser utilizadas para generar todas las soluciones de la ecuación dada. Utilice una utilidad gráfica para graficar cada lado de la ecuación dada para verificar sus soluciones.

\[2\sin(x) - 1 = 0\]
\[2\cos(x) + 1 = 0\]
\[2\sin(x) + \sqrt{2} = 0\]
\[4\cos(x) - 3 = 0\]
\[3\sin^{2}(x) - 2\sin(x) = 0\]
\[\sin(x)\cos^{2}(x) = 2\sin(x)\]
\[\cos^{2}(x) + 4\sin(x) = 4\]
\[5\cos(x) + 4 = 2\sin^{2}(x)\]
\[3\tan^{2}(x) - 1 = 0\]
\[\tan^{2}(x) - \tan(x) = 6\]

Contestar

(a)\(x = \dfrac{\pi}{6} + k(2\pi)\) o\(x = \dfrac{5\pi}{6} + k(2\pi)\), donde\(k\) es un entero.

b)\(x = \dfrac{2\pi}{3} + k(2\pi)\) o\(x = \dfrac{4\pi}{3} + k(2\pi)\), donde\(k\) es un número entero.

d)\(x = \cos^{-1}(\dfrac{3}{4} + k(2\pi)\) o\(x = \cos^{-1}(-\dfrac{3}{4} + k(2\pi)\), donde\(k\) es un número entero.

(f)\(x = k\pi\), donde\(k\) es un entero.

Ejercicio\(\PageIndex{5}\)

Se pide a un alumno que aproxime todas las soluciones en grados (a dos decimales) a la ecuación\(\sin(\theta) + \dfrac{1}{3} = 1\) en el\(0^\circ \leq \theta \leq 360^\circ\) intervalo.El alumno proporciona la respuesta\(\theta = \sin^{-1}(\dfrac{2}{3}) \approx 41.81^\circ\). ¿El alumno dio la respuesta correcta al problema señalado? Explique.

Contestar

\(\theta = \sin^{-1}(\dfrac{2}{3}) \approx 41.81^\circ\)es una solución de la ecuación\(\sin(\theta) + \dfrac{1}{3} = 1\) con\(0 \leq \theta \leq 360^\circ\). Hay otra solución (en el segundo cuadrante) para esta ecuación con\(0 \leq \theta \leq 360^\circ\).

Ejercicio\(\PageIndex{6}\)

La cristalografía de rayos X es una herramienta importante en química. Una aplicación de la cristalografía de rayos X es descubrir las macromoléculas de estructura atómica. Por ejemplo, la estructura de doble hélice del ADN se encontró mediante cristalografía de rayos X.

La idea básica detrás de la cristalografía de rayos X es la siguiente: dos haces de rayos X con la misma longitud de onda\(\lambda\) y fase se dirigen en ángulo\(\theta\) hacia un cristal compuesto por átomos dispuestos en una red en planos separados por una distancia\(d\) como se ilustra en la Figura 4.5.1 Los haces se reflejan diferentes átomos (etiquetados como\(P\) y\(Q\) en la Figura 4.5) dentro del cristal. Un haz de rayos X (el inferior como se ilustra en la Figura 4.5) debe recorrer una distancia mayor que el otro. Cuando se reflejan, los rayos X se combinan pero, debido al desplazamiento de fase del haz inferior, la combinación podría tener una amplitud pequeña o una amplitud grande. La Ley de Bragg establece que la suma de los rayos reflejados tendrá amplitud máxima cuando la longitud extra que el haz más largo tenga que recorrer es igual a un múltiplo entero de la longitud\(\lambda\) de onda de la radiación. En otras palabras,\[n\lambda = 2d\sin(\theta),\]

para algún número entero positivo\(n\). Supongamos que\(\lambda = 1.54\) angstroms y\(d = 2.06\) angstroms. Aproximar a dos decimales el valor más pequeño de\(\theta\) (en grados) para el cual\(n = 1\).

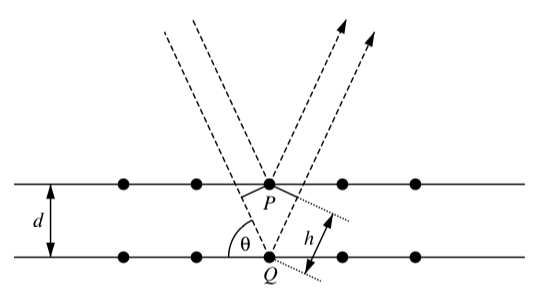
Figura\(\PageIndex{1}\): Rayos X reflejados a partir de átomos de cristal.

Ejercicio\(\PageIndex{7}\)

Utilice una identidad de suma o diferencia apropiada para encontrar el valor exacto de cada una de las siguientes.

1. \(\cos(-10^\circ)\cos(35^\circ) + \sin(-10^\circ)\sin(35^\circ)\)
2. \(\cos(\dfrac{7\pi}{9})\cos(\dfrac{2\pi}{9}) - \sin(\dfrac{7\pi}{9})\sin(\dfrac{2\pi}{9}))\)
3. \(\sin(\dfrac{7\pi}{9})\cos(\dfrac{2\pi}{9}) + \cos(\dfrac{7\pi}{9})\sin(\dfrac{2\pi}{9}))\)
4. \(\sin(80^\circ)\cos(55^\circ) + \cos(80^\circ)\sin(55^\circ)\)

Contestar

1. \(\cos(-10^\circ - 35^\circ) = \cos(-45^\circ) = \dfrac{\sqrt{2}}{2}\).
2. \(\cos(\dfrac{7\pi}{9} + \dfrac{2\pi}{9}) = \cos(\pi) = -1\)

Ejercicio\(\PageIndex{8}\)

Ángulos\(A\) y\(B\) están en posición estándar y\(\sin(\dfrac{1}{2}, \cos(A) > 0)\),\(\cos(B) = \dfrac{3}{4}\), y\(\sin(B) < 0\). Dibuja una imagen de los ángulos\(A\) y\(B\) en el plano y luego encuentra cada uno de los siguientes.

1. \(\cos(A + B)\)
2. \(\cos(A - B)\)
3. \(\sin(A + B)\)
4. \(\sin(A - B)\)
5. \(\tan(A + B)\)
6. \(\tan(A - B)\)

Contestar

Primero usamos la Identidad Pitagórica para determinar\(\cos(A)\) y\(\sin(B)\). A partir de esto, obtenemos\[\cos(A) = \dfrac{\sqrt{3}}{2}\] y\[\sin(B) = -\dfrac{\sqrt{7}}{4}\]

(a)\[\cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B) = \dfrac{\sqrt{3}}{2}\cdot\dfrac{3}{4} - \dfrac{1}{2}\cdot(-\dfrac{\sqrt{7}}{4}) = \dfrac{3\sqrt{3} + \sqrt{7}}{8}\]

Ejercicio\(\PageIndex{9}\)

Identificar ángulos\(A\) y\(B\) en los que conocemos los valores del coseno y seno para que se pueda utilizar una identidad de suma o diferencia para calcular el valor exacto de la cantidad dada. (Por ejemplo,\(15^\circ = 45^\circ - 30^\circ\).)

1. \(\cos(15^\circ)\)
2. \(\sin(75^\circ)\)
3. \(\tan(105^\circ)\)
4. \(\sec(345^\circ)\)

Contestar

(a)\(\cos(15^\circ) = \cos(45^\circ - 30^\circ) = \dfrac{\sqrt{6} + \sqrt{2}}{4}\)

(b) Podemos utilizar\(345^\circ = 300^\circ + 45^\circ\) y evaluar primero\(\cos(345^\circ)\). Esto da\(\cos(345^\circ) = \dfrac{\sqrt{6} + \sqrt{2}}{4}\) y\(\sec(345^\circ) = \dfrac{4}{\sqrt{6} + \sqrt{2}}\). También podríamos haber aprovechado el hecho de que\(\cos(345^\circ) = \cos(15^\circ)\) y el resultado en la parte (a).

Ejercicio\(\PageIndex{10}\)

Verifique las identidades de suma y diferencia para la tangente:

\[\tan(A - B) = \dfrac{\tan(A) - \tan(B)}{1 + \tan(A)\tan(B)}\]y
\[\tan(A + B) = \dfrac{\tan(A) + \tan(B)}{1 - \tan(A)\tan(B)}\]

Ejercicio\(\PageIndex{11}\)

Verificar las identidades de la cofunción

1. \(\cot(\dfrac{\pi}{2} - x) = \tan(x)\)
2. \(\sec(\dfrac{\pi}{2} - x) = \csc(x)\)
3. \(\csc(\dfrac{\pi}{2} - x) = \sec(x)\)

Contestar

(a)\[\cot(\dfrac{\pi}{2} - x) = \dfrac{\cos(\dfrac{\pi}{2} - x)}{\sin(\dfrac{\pi}{2} - x)} = \dfrac{\sin(x)}{\cos(x)} = \tan(x)\]

Ejercicio\(\PageIndex{12}\)

Dibuja gráficas para determinar si una ecuación dada es una identidad. Verificar aquellas ecuaciones que son identidades y proporcionar ejemplos para mostrar que las otras no son identidades.

1. \(\sin(x + \dfrac{\pi}{4}) + \sin(x - \dfrac{\pi}{4}) = 2\sin(x)\cos(\dfrac{\pi}{4})\)
2. \(\sin(210^\circ + x) - \cos(210^\circ + x) = 0\)

Ejercicio\(\PageIndex{13}\)

Determinar si las siguientes ecuaciones son identidades.

1. \(\dfrac{\sin(r + s)}{\cos(r)\cos(s)} = \tan(r) + \tan(s)\)
2. \(\dfrac{\sin(r - s)}{\cos(r)\cos(s)} = \tan(r) - \tan(s)\)

Ejercicio\(\PageIndex{14}\)

Utilizar una identidad apropiada para resolver la ecuación dada.

1. \(\sin(\theta)\cos(35^\circ) = \cos(\theta)\sin(35^\circ) = \dfrac{1}{2}\)
2. \(\cos(2x)\cos(x) = \sin(2x)\sin(x) = -1\)

Ejercicio\(\PageIndex{15}\)

1. Utilice un dispositivo de gráficos para dibujar la gráfica de\(f(x) = \sin(x) + \cos(x)\) uso\(-\pi \leq x \leq 2\pi\) y\(-2 \leq y \leq 2\). ¿La gráfica de esta función parece ser una sinusoide? Si es así, aproximar la amplitud y el desplazamiento de fase de la sinusoide. Cuál es el periodo de esta sinusoide.
2. Utilice una de las identidades de suma para reescribir la expresión\(\sin(x + \dfrac{\pi}{4})\). Luego use los valores de\(\sin(\dfrac{\pi}{4})\) y\(\cos(\dfrac{\pi}{4})\) para reescribir aún más la expresión.
3. Utilice el resultado de la parte (b) para mostrar que la función\(f(x) = \sin(x) + \cos(x)\) es de hecho una función sinusoidal. ¿Cuál es su amplitud, desplazamiento de fase y período?

Ejercicio\(\PageIndex{16}\)

1. Utilice un dispositivo de gráficos para dibujar la gráfica de\(g(x) = \sin(x) + \sqrt{3}\cos(x)\) uso\(-\pi \leq x \leq 2\pi\) y\(-2.5 \leq y \leq 2.5\). ¿La gráfica de esta función parece ser una sinusoide? Si es así, aproximar la amplitud y el desplazamiento de fase de la sinusoide. Cuál es el periodo de esta sinusoide.
2. Utilice una de las identidades de suma para reescribir la expresión\(\sin(x + \dfrac{\pi}{3})\). Luego use los valores de\(\sin(\dfrac{\pi}{3})\) y\(\cos(\dfrac{\pi}{3})\) para reescribir aún más la expresión.
3. Utilice el resultado de la parte (b) para mostrar que la función\(g(x) = \sin(x) + \sqrt{3}\cos(x)\) es de hecho una función sinusoidal. ¿Cuál es su amplitud, desplazamiento de fase y período?

Ejercicio\(\PageIndex{17}\)

Cuando se aplican dos voltajes a un circuito, el voltaje resultante en el circuito será la suma de los voltajes individuales. Supongamos dos voltajes\(V_{1}(t) = 30\sin(120\pi t)\) y\(V_{2}(t) = 40\cos(120\pi t)\) se aplican a un circuito. La gráfica de la suma\(V(t) = V_{1}(t) + V_{2}(t)\) se muestra en la Figura 4.8.

1. Utilice la gráfica para estimar los valores de\(C\) para que\[y = 50\sin(120\pi(t - c))\] se ajuste a la gráfica de\(V\).
2. Utilice la Identidad de Diferencia Sinusoidal para reescribir\(50\sin(120\pi(t - c))\) como una expresión de la forma\(50\sin(A)\cos(B) - 50\cos(A)\sin(B)\) donde\(A\) e\(B\) involucrar\(t\) y/o\(C\). A partir de esto, determinar un valor de C que hará

   \[30\sin(120\pi t) + 40\cos(120\pi t) = 50\sin(120\pi(t - c))\].Compara este valor\(C\) con el que estimaste en la parte (a).

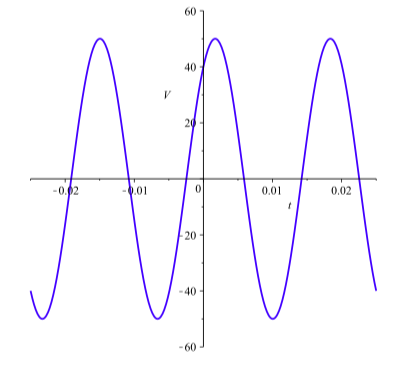
Figura\(\PageIndex{2}\): Gráfica de\(V(t) = V_{1}(t) + V_{2}(t)\).

Ejercicio\(\PageIndex{18}\)

Dado que\(\cos(\theta) = \dfrac{2}{3})\) y\(\sin(\theta) < 0\), determinar los valores exactos de\(\sin(2\theta)\),\(\cos(2\theta)\), y\(\tan(2\theta)\).

Contestar

Utilizar la Identidad Pitagórica para obtener\(\sin^{2}(\theta) = \dfrac{5}{9}\). Ya que\(\sin(\theta) < 0\), vemos eso\(\sin(\theta) = -\dfrac{\sqrt{5}}{3}\). Ahora use identidades de doble ángulo apropiadas para obtener\[\sin(2\theta) = -\dfrac{4\sqrt{5}}{9}\]\[\cos(2\theta) = -\dfrac{1}{9}\]

Luego use\(\tan(2\theta) = \dfrac{\sin(2\theta)}{\cos(2\theta)} = 4\sqrt{5}\).

Ejercicio\(\PageIndex{19}\)

Encuentra todas las soluciones a la ecuación dada. Utilice una utilidad gráfica para graficar cada lado de la ecuación dada para verificar sus soluciones.

1. \(\cos(x)\sin(x) = \dfrac{1}{2}\)
2. \(\cos(2x) + 3 = 5\cos(x)\)

Contestar

(a)\(x = \dfrac{\pi}{4} + k\pi\), donde\(k\) es un entero.

Ejercicio\(\PageIndex{20}\)

Determinar cuál de las siguientes ecuaciones es una identidad. Verifica tus respuestas.

1. \(\cot(t)\sin(2t) = 1 + \cos(2t)\)
2. \(\sin(2x) = \dfrac{2 - \csc^{2}(x)}{\csc^{2}(x)}\)
3. \(\cos(2x) = \dfrac{2 - \sec^{2}(x)}{\sec^{2}(x)}\)

Contestar

(a) Se trata de una identidad. Comience con el lado izquierdo de la ecuación y use\(\cot(t) = \dfrac{\cos(t)}{\sin(t)}\) y\(\sin(2t) = 2\sin(t)\cos(t)\).

Ejercicio\(\PageIndex{21}\)

Encuentre una fórmula más simple para\(\cos(\pi + x)\) en términos de\(\cos(x)\). Ilustrar con una gráfica.

Ejercicio\(\PageIndex{22}\)

Un compañero de clase comparte su solución al problema de resolver a\(\sin(2x) = 2\cos(x)\) lo largo del intervalo\([0, 2\pi)\). Ha escrito

\[\sin(2x) = 2\cos(x)\]
\[\dfrac{\sin(2x)}{2} = \cos(x)\]
\[\sin(x) = \cos(x)\]
\[\tan(x) = 1\]

así\(x = \dfrac{\pi}{4}\) o\(x = \dfrac{5\pi}{4}\)

1. Dibuja gráficas de\(\sin(2x)\)\(2\cos(x)\) y explica por qué este compañeros de clase
2. Encuentra el error en el argumento de este compañero de clase.
3. Determinar las soluciones a\(\sin(2x) = 2\cos(x)\) lo largo del intervalo\([0, 2\pi)\).

Ejercicio\(\PageIndex{23}\)

Determinar el valor exacto de cada uno de los siguientes:

1. \(\sin(22.5^\circ)\)
2. \(\cos(22.5^\circ)\)
3. \(\tan(22.5^\circ)\)
4. \(\sin(15^\circ)\)
5. \(\cos(15^\circ)\)
6. \(\tan(15^\circ)\)
7. \(\sin(195^\circ)\)
8. \(\cos(195^\circ)\)
9. \(\tan(195^\circ)\)

Contestar

a)\(\sin(22.5^\circ) = \sqrt{\dfrac{1 - \dfrac{\sqrt{2}}{2}}{2}} = \dfrac{1}{2}\sqrt{2 - \sqrt{2}}\).

c)\(\tan(22.5^\circ) = \sqrt{\dfrac{2 - \sqrt{2}}{2 + \sqrt{2}}} = \sqrt{3 - 2\sqrt{2}}\)

h)\(\cos(195^\circ) = -\sqrt{\dfrac{1 + \dfrac{\sqrt{3}}{2}}{2}} = -\dfrac{1}{2}\sqrt{2 + \sqrt{3}}\)

Ejercicio\(\PageIndex{24}\)

Determinar el valor exacto de cada uno de los siguientes:

1. \(\sin(\dfrac{3\pi}{8})\)
2. \(\cos(\dfrac{3\pi}{8})\)
3. \(\tan(\dfrac{3\pi}{8})\)
4. \(\sin(\dfrac{5\pi}{8})\)
5. \(\cos(\dfrac{5\pi}{8})\)
6. \(\tan(\dfrac{5\pi}{8})\)
7. \(\sin(\dfrac{11\pi}{12})\)
8. \(\cos(\dfrac{11\pi}{12})\)
9. \(\tan(\dfrac{11\pi}{12})\)

Contestar

(a)\(\sin(\dfrac{3\pi}{8}) = \sqrt{\dfrac{1 + \dfrac{\sqrt{2}}{2}}{2}} = \dfrac{1}{2}\sqrt{2 + \sqrt{2}}\)
(c)\(\tan(\dfrac{3\pi}{8}) = \sqrt{\dfrac{2 + \sqrt{2}}{2 - \sqrt{2}}} = \sqrt{3 + 2\sqrt{2}}\)
(h)\(\cos(\dfrac{11\pi}{12}) = -\sqrt{\dfrac{1 + \dfrac{\sqrt{3}}{2}}{2}} = -\dfrac{1}{2}\sqrt{2 + \sqrt{3}}\)

Ejercicio\(\PageIndex{25}\)

Si\(\cos(x) = \dfrac{2}{3}\) y\(\sin(x) < 0\) y\(0 \leq x \leq 2\pi\), determinar el valor exacto de cada uno de los siguientes:

1. \(\cos(\dfrac{x}{2})\)
2. \(\sin(\dfrac{x}{2})\)
3. \(\tan(\dfrac{x}{2})\)

Contestar

a) Observamos que desde\(\dfrac{3\pi}{2} \leq x \leq 2\pi, \dfrac{3\pi}{4} \leq \dfrac{x}{2} \leq \pi\).

\[\sin(\dfrac{x}{2}) = \sqrt{\dfrac{1 - \dfrac{2}{3}}{2}} = \dfrac{1}{\sqrt{6}}\]

Ejercicio\(\PageIndex{26}\)

Si\(\sin(x) = \dfrac{2}{5}\) y\(\cos(x) < 0\) y\(0 \leq x \leq 2\pi\), determinar el valor exacto de cada uno de los siguientes:

1. \(\cos(\dfrac{x}{2})\)
2. \(\sin(\dfrac{x}{2})\)
3. \(\tan(\dfrac{x}{2})\)

Ejercicio\(\PageIndex{27}\)

Un rectángulo se inscribe en un semicírculo de radio\(r\) como se muestra en el diagrama de la siguiente manera.

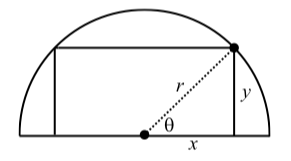
Figura\(\PageIndex{3}\)

Podemos escribir el área\(A\) de este rectángulo como\(A = (2x)y\).

1. Escribe el área de este rectángulo inscrito en función del ángulo que\(\theta\) se muestra en el diagrama y luego muéstralo\(A = r^{2}\sin(2\theta)\).
2. Utilice la fórmula de la parte (a) para determinar el ángulo\(\theta\) que produce el mayor valor de\(A\) y determinar las dimensiones de este rectángulo inscrito con el área más grande posible.

Ejercicio\(\PageIndex{28}\)

Derivar la identidad de ángulo triple
\[\sin(3A) = -4\sin^{3}(A) + 2\sin(A)\]

para el seno con los siguientes pasos.

1. Escribir\(3A\) como\(2A + A\) y aplicar la Identidad Sine Sum para escribir\(\sin(3A)\) en términos de\(\sin(2A)\) y\(\sin(2A)\),
2. Utilice la Identidad de Doble Ángulo para escribir\(\sin(2A)\) en términos de\(\sin(A)\)\(\cos(A)\) y y escribir\(\cos(2A)\) en términos de\(\sin(A)\).
3. Usa una identidad pitagórica para escribir\(\cos^{2}(2A)\) en términos de\(\sin^{2}(A)\) y simplificar.

Ejercicio\(\PageIndex{29}\)

Derivar la identidad de ángulo cuádruple

\[\sin(4x) = 4\cos(x)[\sin(x) - 2\sin^{3}(x)]\]como se indica a continuación.

1. Escribe s\[\sin(4x) = \sin(2(2x))\] y usa la Identidad de Doble Ángulo para seno para reescribir esta fórmula.
2. Ahora usa la Identidad de Ángulo Doble para seno y una de las Identidades de Doble Ángulo para el coseno para reescribir la expresión desde la parte (a).
3. Algebraicamente reescribir la expresión de la parte (b) para obtener la fórmula deseada para\(\sin(4x)\).

Ejercicio\(\PageIndex{30}\)

Escribe cada una de las siguientes expresiones como una suma de valores de función trigonométrica. Cuando sea posible, determine el valor exacto de la expresión resultante.

1. \[\sin(37.5^\circ)\cos(7.5^\circ)\]
2. \[\sin(75^\circ)\sin(15^\circ)\]
3. \[\cos(44^\circ)\cos(16^\circ)\]
4. \[\cos(45^\circ)\cos(15^\circ)\]
5. \[\cos(\dfrac{5\pi}{12})\sin(\dfrac{\pi}{12})\]
6. \[\sin(\dfrac{3\pi}{4})\cos(\dfrac{\pi}{12})\]

Contestar

(a)\(\sin(37.5^\circ)\cos(7.5^\circ) = \dfrac{1}{2}[\sin(45^\circ) + \sin(30^\circ)] = \dfrac{\sqrt{2} + 1}{4}\)

e)\(\cos(\dfrac{5\pi}{12})\sin(\dfrac{\pi}{12}) = \dfrac{1}{2}[\sin(\dfrac{\pi}{2}) - \sin(\dfrac{\pi}{3})] = \dfrac{1 - \sqrt{3}}{4}\)

Ejercicio\(\PageIndex{31}\)

Escribe cada una de las siguientes expresiones como una suma de valores de función trigonométrica. Cuando sea posible, determine el valor exacto de la expresión resultante.

1. \[\sin(50^\circ) + \sin(10^\circ)\]
2. \[\sin(195^\circ) - \sin(105^\circ)\]
3. \[\cos(195^\circ) - \cos(15^\circ)\]
4. \[\cos(76^\circ) + \cos(14^\circ)\]
5. \[\cos(\dfrac{7\pi}{12}) + \cos(\dfrac{\pi}{12})\]
6. \[\sin(\dfrac{7\pi}{4}) - \sin(\dfrac{5\pi}{12})\]

Contestar

(a)\(\sin(50^\circ) + \sin(10^\circ) = 2\sin(30^\circ)\cos(20^\circ) = \cos(20^\circ)\)

e)\(\cos(\dfrac{7\pi}{12}) + \cos(\dfrac{\pi}{12}) = 2\cos(\dfrac{\pi}{3})\cos(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}\)

Ejercicio\(\PageIndex{32}\)

Encuentra todas las soluciones a la ecuación dada. Utilice una utilidad gráfica para graficar cada lado de la ecuación dada para verificar sus soluciones.

1. \[\sin(2x) + \sin(x) = 0\]
2. \[\sin(x)\cos(x) = \dfrac{1}{4}\]
3. \[\cos(2x) + \cos(x) = 0\]

Contestar

(a)\[\sin(2x) + \sin(x) = 0\]

\[2\sin(\dfrac{3x}{2})\cos(\dfrac{x}{2}) = 0\]

Entonces\[\sin(\dfrac{3x}{2}) = 0\] o\[\cos(\dfrac{x}{2}) = 0\]. Esto da\[x = k\pi\] o\[x = \dfrac{2\pi}{3} + k(2\pi)\] o\[x = \dfrac{4\pi}{3} + k(2\pi)\], donde\(k\) es un entero.