5.6: Intervenciones asignadas a grupos

Los métodos descritos en las Secciones 3 a 5 asumen todos que los individuos van a ser las unidades de asignación. Es decir, los grupos de prueba se construirán de manera efectiva haciendo una lista completa de los individuos disponibles para el juicio y seleccionando aleatoriamente qué individuos se van a asignar a cada grupo de prueba. Como se explica en el Capítulo 4, Sección 4, sin embargo, muchos juicios de campo no se organizan de esta manera. En cambio, se asignan grupos de individuos a las intervenciones en estudio. Estos grupos suelen denominarse clusters y pueden corresponder a comunidades, por ejemplo, pueblos, caseríos, o sectores definidos de un área urbana; instituciones como escuelas o lugares de trabajo; o pacientes que atienden a un centro de salud en particular.

Los ensayos en los que comunidades u otros tipos de conglomerados se asignan aleatoriamente a los diferentes grupos del ensayo se conocen como ensayos aleatorizados por conglomerados, y los cálculos del tamaño de la muestra para dichos ensayos se presentan en la Sección 6.1. Los ensayos de cuña escalonada son una forma modificada de ensayo aleatorizado por conglomerados y se discuten en la Sección 6.2.

6.1 Ensayos aleatorizados por conglomerados

Si los clústeres se asignan aleatoriamente a los diferentes brazos de prueba, el clúster también debe ser utilizado como unidad de análisis, aunque las evaluaciones de resultados se realicen sobre individu- ales dentro de los clústeres (ver Capítulo 21, Sección 8). Por ejemplo, supongamos que el ensayo de mosquito-net se va a realizar de la siguiente manera. Varios pueblos (digamos 20) deben dividirse aleatoriamente en dos grupos de igual tamaño. En los diez pueblos del primer grupo, se entregarán mosquiteros a toda la población de cada poblado, mientras que el segundo grupo de diez pueblos servirá como controles. El análisis del impacto de los mosquito-mosquiteros en la incidencia de la malaria clínica se haría calculando la tasa de incidencia (ajustada por edad) en cada aldea y comparando las diez tasas para las aldeas de intervención con las diez tasas para las aldeas control. Esto se lograría tratando la tasa (ajustada por edad) como el resultado cuantitativo medido para cada aldea y comparándolos, utilizando la prueba t no pareada o la prueba de suma de rangos no paramétricos (ver Capítulo 21, Sección 8). Si se analizan las proporciones y no las tasas de incidencia, el principio es el mismo: la proporción (ajustada por edad) se trataría como el resultado cuantitativo para cada conglomerado.

Cuando la asignación es por conglomerado, las fórmulas del tamaño del ensayo tienen que ajustarse para permitir la variación intrínseca entre comunidades. Supongamos primero que se van a comparar las tasas de incidencia en los dos grupos. El número requerido de clústeres c viene dado por:

\ [
c=1+\ izquierda (z_ {1} +z_ {2}\ derecha) ^ {2}\ izquierda [\ izquierda (r_ {1} +r_ {2}\ derecha)/y+k^ {2}\ izquierda (r_ {1} ^ {2} +r_ {2} ^ {2}\ derecha)\ derecha]/\ izquierda (r_ {1} -r_ {2}\ derecha) ^ {2}
\]

En esta fórmula, y es la persona-años de observación en cada conglomerado, mientras que r 1 y r2 son las tasas promedio en los conglomerados de intervención y control, respectivamente. La variación intrínseca entre conglomerados se mide por k, el coeficiente de variación de las tasas de incidencia (verdaderas) entre los conglomerados de cada grupo, y se define como la desviación estándar de las tasas divididas por la tasa promedio. El valor de k se asume similar en los grupos de intervención y control, de manera que la variabilidad relativa sigue siendo la misma intervención posterior.

Si se van a comparar proporciones, el número requerido de conglomerados viene dado por:

\ [
c=1+\ izquierda (z_ {1} +z_ {2}\ derecha) ^ {2}\ izquierda [2 p (1-p)/n+k^ {2}\ izquierda (p_ {1} ^ {2} +p_ {2} ^ {2}\ derecha)\ derecha]/\ izquierda (p_ {1} -p_ {2}\ derecha) ^ {2}
\]

En esta fórmula, n es el tamaño del ensayo en cada comunidad; p 1 y p 2 son las proporciones promedio en los grupos de intervención y control, respectivamente; p es el promedio de p 1 y p 2, y k es el coeficiente de variación de las proporciones (verdaderas) entre los clusters de cada grupo.

A veces se dispondrá de una estimación de k a partir de datos previos sobre los mismos conglomerados o de un estudio piloto. Si no se dispone de datos, puede ser necesario hacer una suposición arbitraria, pero plausible, sobre el valor de k. Por ejemplo, k = 0.25 implica que las tasas verdaderas en cada grupo varían aproximadamente entre r i ±2 kr i, es decir, entre 0.5 r y 1.5 r. En general, es poco probable que k supere 0.5.

Ejemplo: Supongamos que el ensayo mosquitero se va a realizar asignando la inter- vención a nivel de aldea. La tasa de incidencia de malaria clínica en niños antes de la intervención es de 10 por cada 1000 niños-semanas de observación, y el ensayo debe diseñarse para dar 90% de potencia si la intervención reduce la tasa de incidencia en 50%. Hay alrededor de 50 niños elegibles por aldea, y se pretende continuar el seguimiento por 1 año, de manera que y es aproximadamente 2500 niños-semanas. No se dispone de información sobre la variación entre aldeas en las tasas de incidencia. Tomando, el número de pueblos requeridos por grupo viene dado por lo siguiente, de manera que se necesitarían aproximadamente siete aldeas en cada grupo:

\ [
c=1+ (1.96+1.28) ^ {2}\ izquierda [(0.01+0.005)/2500+0.25^ {2}\ izquierda (0.01^ {2} +0.005^ {2}\ derecha)\ derecha]/(0.01-0.005) ^ {2} =6.8
\]

Obsérvese que esto daría un total de 17 500 niños-semanas de observación en cada grupo, en comparación con 6300 niños-semanas si los niños individuales fueran aleatorizados para recibir mosquiteros. En la Figura 5.2 se muestra el número de aldeas requeridas en cada grupo, despendientes de las semanas infantiles de observación por aldea y el valor de k.

El efecto de la asignación grupal en el tamaño total del ensayo necesario dependerá del grado en que los individuos dentro de un clúster tengan más probabilidades de ser similares entre sí que los individuos en un clúster diferente para la medida de resultado en el ensayo. Si no hay het- erogeneidad entre clusters en el resultado de interés, en el sentido de que la variación entre las tasas o medias específicas de clúster no es mayor de lo que se esperaría que ocurriera por casualidad, debido a variaciones de muestreo, el tamaño total del ensayo será aproximadamente el mismo que si las intervenciones fueran destinados a particulares. Para la mayoría de los resultados, sin embargo, habrá diferencias reales entre los conglomerados y, en estas circunstancias, el tamaño de prueba requerido será mayor que con la asignación individual. La relación de los tamaños de prueba requeridos con asignación de clúster e individual a veces se denomina efecto de diseño. Sin embargo, no se puede asumir ningún valor único para el efecto de diseño, ya que su valor depende de la variabilidad del resultado de interés entre clústeres y de los tamaños de los conglomerados, por lo que se recomienda estimar explícitamente el tamaño de muestra requerido.

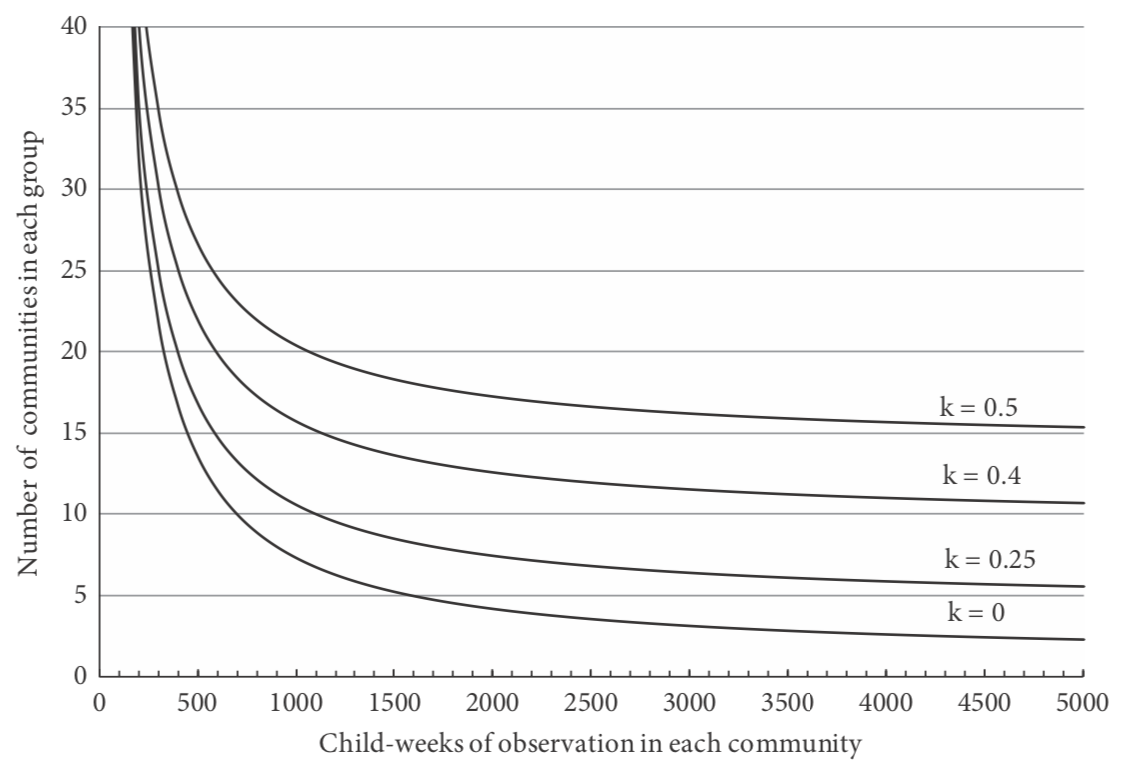
Figura 5.2 Número de comunidades requeridas en cada grupo en un ensayo del efecto de mosquito-mosquiteros contra la malaria clínica.

Obsérvese que, aunque los cálculos sugieran que se requieren menos de cuatro clusters en cada grupo, es preferible tener al menos cuatro en cada grupo. Con tan pocas unidades de ob- servación, generalmente se prefiere para el análisis el uso de procedimientos no paramétricos, como la prueba de suma de rangos, y se necesita un tamaño de muestra de al menos cuatro en cada grupo para tener alguna posibilidad de obtener un resultado significativo cuando se usa esta prueba.

Es posible reducir el número requerido de comunidades mediante la adopción de un diseño emparejado. Por ejemplo, esto se puede hacer utilizando el estudio basal para organizar los clusters en pares, en los que las tasas del resultado de interés son similares, y seleccionando aleatoriamente un miembro de cada par para recibir la intervención. Sin embargo, es difícil cuantificar el efecto de este enfoque sobre el número de conglomerados requeridos. Para ello, se requiere información sobre la variabilidad del efecto del tratamiento entre com- munidades y sobre la medida en que los datos basales son predictivos de las tasas que se observarían durante el periodo de seguimiento en ausencia de intervención, y esta información rara vez está disponible. Con un diseño pareado, se requieren al menos seis clusters en cada grupo para poder obtener una diferencia significativa mediante una prueba estadística no paramétrica.

Se da más información sobre los cálculos del tamaño de la muestra para ensayos aleatorizados por conglomerados en Hayes y Bennett (1999) y Hayes y Moulton (2009).

De acuerdo con el número de niños-semanas de observación en cada comunidad y el grado de variación en las tasas de malaria clínica entre comunidades (k es el coeficiente de variación de las tasas de incidencia; ver texto). Se supone que la tasa promedio de incidencia de malaria clínica en ausencia de la intervención es de diez por cada 10 000 semanas de observación, y se requiere que el ensayo tenga 90% de poder para detectar una reducción de 50% en la incidencia de malaria en el nivel p < 0.05 de significancia estadística.

6.2 Ensayos de cuña escalonada

El diseño de cuña escalonada se introdujo en el Capítulo 4, Sección 4.3 y es una modi- ficación del ensayo aleatorizado por conglomerados, en el que todos los conglomerados comienzan el ensayo en el grupo control. A continuación, la intervención se introduce gradualmente en los conglomerados en orden aleatorio, hasta que, al final del ensayo, todos los clusters están en el grupo de intervención.

Una consecuencia del diseño de cuña escalonada es que, en la mayoría de los momentos del ensayo, habrá un número desigual de conglomerados en los grupos de intervención y control. Esto significa que, cuando se contabilizan las tendencias seculares comparando la intervención con los grupos de control en cada paso, un ensayo de cuña escalonada puede tener menor potencia y precisión que un ensayo aleatorizado de conglomerados estándar del mismo tamaño, en el que los números de conglomerados de in- tervention y control son iguales en todo. Cuando hay cero correlación intra-cluster, el ensayo necesitará hasta un 50% más de clusters. Para ajustar esto, el número de clústeres tiene que ser multiplicado por un factor de corrección que depende del número de 'pasos' en el diseño de cuña escalonada. Si hay cinco pasos, el factor de corrección es 1.3, elevándose a aproximadamente 1.4 para números de pasos entre 10 y 20. Cuando la correlación intra-cluster es lo suficientemente grande, la ganancia en eficiencia que se puede obtener aprovechando la información pre—post de cada clúster puede superar este factor, haciendo que un ensayo de cuña escalonado sea más eficiente que un ensayo paralelo. Para ser conservadores, sin embargo, puede ser mejor inflar el número de racimos.

Ejemplo: En el ensayo de mosquito-net discutido anteriormente, el cálculo del tamaño de la muestra mostró que necesitábamos siete racimos en cada brazo o un total de 14 racimos. Si ahora proponemos llevar a cabo este ensayo utilizando un ensayo de cuña escalonada, una corrección conservadora sería multiplicar este número por 1.4, dando 20 conglomerados. Por ejemplo, esto podría implementarse con diez pasos a lo largo de un período de 5 años, proporcionando redes a dos agrupaciones elegidas aleatoriamente cada medio año.