2.5: El algoritmo de Needleman-Wunsch
- Page ID
- 54691
Ahora utilizaremos la programación dinámica para abordar el problema más difícil de la alineación general de secuencias. Dadas dos cadenas\(S =(S1, . . . , Sn)\) y\(T =(T1, . . . , Tm)\), queremos encontrar la subsecuencia común más larga, que puede o no contener huecos. En lugar de maximizar la longitud de una subsecuencia común, queremos calcular la subsecuencia común que optimice la puntuación según lo definido por nuestra función de puntuación. Que d denote el costo de penalización por gap y\(s(x; y)\) la puntuación de alinear una base x y una base y, estos se deducen de las probabilidades de inserción/deleción y sustitución que se pueden determinar experimentalmente o observando secuencias que sabemos que están estrechamente relacionadas. El algoritmo que desarrollaremos en las siguientes secciones para resolver la alineación de secuencias se conoce como el algoritmo Needleman-Wunsch.
Programación dinámica vs. memorización
Antes de sumergirnos en el algoritmo, una nota final sobre la memorización está en orden. Al igual que el problema de Fibonacci, el problema de alineación de secuencias se puede resolver en un enfoque de arriba hacia abajo o de abajo hacia arriba.
En un enfoque recursivo de arriba hacia abajo podemos usar la memoización para crear un diccionario potencialmente grande indexado por cada uno de los subproblemas que estamos resolviendo (secuencias alineadas). Esto requiere\(O\left(n^{2} m^{2}\right)\) espacio si indexamos cada subproblema por los puntos inicial y final de las subsecuencias para las que se necesita calcular una alineación óptima. La ventaja es que resolvemos cada subproblema a lo sumo una vez: si no está en el diccionario, el problema se calcula y luego se inserta en el diccionario para mayor referencia.
En un enfoque iterativo de abajo hacia arriba podemos usar programación dinámica. Definimos el orden de los subproblemas de computación de tal manera que una solución a un problema se computa una vez que se han resuelto los subproblemas relevantes. En particular, los subproblemas más simples vendrán antes que los más complejos. Esto elimina la necesidad de realizar un seguimiento de qué subproblemas se han resuelto (el diccionario en memorización se convierte en una matriz) y asegura que no haya trabajo duplicado (cada subalineación se calcula solo una vez).
Así, en este caso particular, la única diferencia práctica entre memorización y programación dinámica es el costo de las llamadas recursivas incurridas en el caso de memorización (el uso del espacio es el mismo).
Declaración del problema
Supongamos que tenemos un alineamiento óptimo para dos secuencias\(S_{1 \ldots n}\) y\(T_{1 \ldots m}\) en el que Si coincide con Tj. La visión clave es que esta alineación óptima se compone de una alineación óptima entre\(\left(S_{1}, \ldots, S_{i-1}\right)\) y\(\left(T_{1}, \ldots, T_{i-1}\right)\) y una alineación óptima entre\(\left(S_{i+1}, \ldots, S_{n}\right)\) y\(\left(T_{j+1}, \ldots, T_{m}\right)\). Esto se desprende de un argumento de cortar y pegar: si una de estas alineaciones parciales es subóptima, entonces cortamos y pegamos una mejor alineación en lugar de la subóptima. Esto logra una mayor puntuación de la alineación general y, por lo tanto, contradice la optimalidad de la alineación global inicial. En otras palabras, cada subrayectoria en una ruta óptima también debe ser óptima. Observe que las puntuaciones son aditivas, por lo que la puntuación de la alineación general es igual a la suma de las puntuaciones de las alineaciones de las subsecuencias. Esto supone implícitamente que los subproblemas de cálculo de las alineaciones de puntuación óptimas de las subsecuencias son independientes. Necesitamos motivar biológicamente que tal suposición conduzca a resultados significativos.
Espacio de índice de subproblemas
Ahora necesitamos indexar el espacio de subproblemas. Dejar\(F_{i,j}\) ser la puntuación de la alineación óptima de\(\left(S_{1}, \ldots, S_{i}\right)\) y\(\left(T_{1}, \ldots, T_{i}\right)\). El espacio de los subproblemas es\(\left\{F_{i, j}, i \in[0,|S|], j \in[0,|T|]\right\}\). Esto nos permite mantener una\( (m + 1) × (n + 1)\) matriz F con las soluciones (es decir, puntuaciones óptimas) para todos los subproblemas.
Optimalidad local
Podemos calcular la solución óptima para un subproblema haciendo una elección local óptima basada en los resultados de los subproblemas más pequeños. Así, necesitamos establecer una función recursiva que muestre cómo la solución a un problema determinado depende de sus subproblemas. Y usamos esta definición recursiva para llenar la tabla F de una manera ascendente.
Podemos considerar las 4 posibilidades (insertar, eliminar, sustituir, emparejar) y evaluar cada una de ellas en función de los resultados que hemos calculado para subproblemas menores. Para inicializar la tabla, establecemos\(F_{0,j} = −j · d\) y\(F_{i,0} = −i·d \) ya que esas son las puntuaciones de alinear\(\left(T_{1}, \ldots, T_{i}\right)\) con j huecos y\(\left(S_{1}, \ldots, S_{i}\right)\) con\(i\) huecos (también conocido como superposición cero entre las dos secuencias). Luego atravesamos la matriz columna por columna calculando la puntuación óptima para cada subproblema de alineación considerando las cuatro posibilidades:
• La Secuencia S tiene un hueco en la posición de alineación actual.
• La Secuencia T tiene un hueco en la posición de alineación actual.
• Hay una mutación (sustitución de nucleótidos) en la posición actual.
• Hay un partido en la posición actual.
Luego utilizamos la posibilidad que produce la puntuación máxima. Expresamos esto matemáticamente por la fórmula recursiva para\(F_{i, j}\):
\[F(0,0)=0\nonumber\]
\[Initialization : F (i, 0) = F (i − 1, 0) − d \nonumber \]
\[F (0, j) = F (0, j − 1) − d \nonumber \]
\ [\ text {Iteración}:\ quad F (i, j) =\ max\ izquierda\ {\ begin {array} {l}
F (i-1, j) -d\ text {insertar hueco en S}\\
F (i, j-1) -d\ text {insertar hueco en T}\\
F (i-1, j-1) +s\ left (x_ {i}, y_ {j}\ right)\ text {coincidencia o mutación}
\ end {array}\ right. \ nonumber\]
Terminación: Inferior derecha
Después de atravesar la matriz, la puntuación óptima para la alineación global viene dada por\(F_{m,n}\). El orden transversal tiene que ser tal que tengamos soluciones a subproblemas dados cuando los necesitamos. Es decir, para calcular\(F_{i,j}\), necesitamos conocer los valores a la izquierda, arriba y diagonalmente arriba\(F_{i,j}\) en la tabla. Así podemos atravesar la tabla en orden mayor de fila o columna o incluso diagonalmente desde la celda superior izquierda hasta la celda inferior derecha. Ahora bien, para obtener la alineación real solo tenemos que recordar las elecciones que hicimos en cada paso.
Solución Óptima
Las trayectorias a través de la matriz\(F\) corresponden a alineaciones de secuencia óptimas. Al evaluar cada celda\(F_{i,j}\) hacemos una elección seleccionando el máximo de las tres posibilidades. Así, el valor de cada celda (no inicializada) en la matriz se determina ya sea por la celda a su izquierda, por encima de ella, o diagonalmente a la izquierda por encima de ella. Una coincidencia y una sustitución se representan como viajando en la dirección diagonal; sin embargo, se puede aplicar un costo diferente para cada uno, dependiendo de si los dos pares de bases que estamos alineando coinciden o no. Para construir la alineación óptima real, necesitamos rastrear a través de nuestras elecciones en la matriz. Es útil mantener un puntero para cada celda mientras se llena la tabla que muestra qué elección se hizo para obtener la puntuación para esa celda. Entonces podemos simplemente seguir nuestros punteros hacia atrás para reconstruir la alineación óptima.
Análisis de soluciones
El análisis de tiempo de ejecución de este algoritmo es muy sencillo. Cada actualización lleva\(O(1)\) tiempo, y como hay mn elementos en la matriz F, el tiempo total de ejecución es\(O(mn)\). De igual manera, el espacio total de almacenamiento es O (mn). Para el caso más general donde la regla de actualización es más complicada, el tiempo de ejecución puede ser más costoso. Por ejemplo, si la regla de actualización requiere probar todos los tamaños de huecos (por ejemplo, el costo de un hueco no es lineal), entonces el tiempo de ejecución sería\(O(mn(m + n))\).
Needleman-Wunsch en la práctica
Supongamos que queremos alinear dos secuencias S y T, donde
S = AGT
T = AAGC
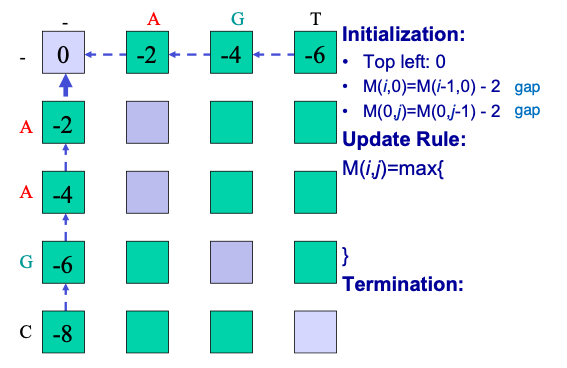
El primer paso es colocar las dos secuencias a lo largo de los márgenes de una matriz e inicializar las celdas de la matriz. Para inicializar asignamos un 0 a la primera entrada de la matriz y luego rellenamos la primera fila y columna con base en la adición incremental de penalizaciones por brecha, como en la Figura 2.9 a continuación. Aunque el algoritmo podría rellenar la primera fila y columna a través de la iteración, es importante definir claramente y establecer límites sobre el problema.
El siguiente paso es la iteración a través de la matriz. El algoritmo procede a lo largo de filas o a lo largo de columnas, considerando una celda a la vez. Para cada celda se calculan tres puntuaciones, dependiendo de las puntuaciones de tres celdas de matriz adyacentes (específicamente la entrada anterior, la diagonal hacia arriba y hacia la izquierda, y la de la izquierda). La puntuación máxima de estos tres trazados posibles se asigna a la entrada y también se almacena el puntero correspondiente. La terminación ocurre cuando el algoritmo llega a la esquina inferior derecha. En la Figura 2.10 la matriz de alineación para las secuencias S y T se ha rellenado con puntajes y punteros.
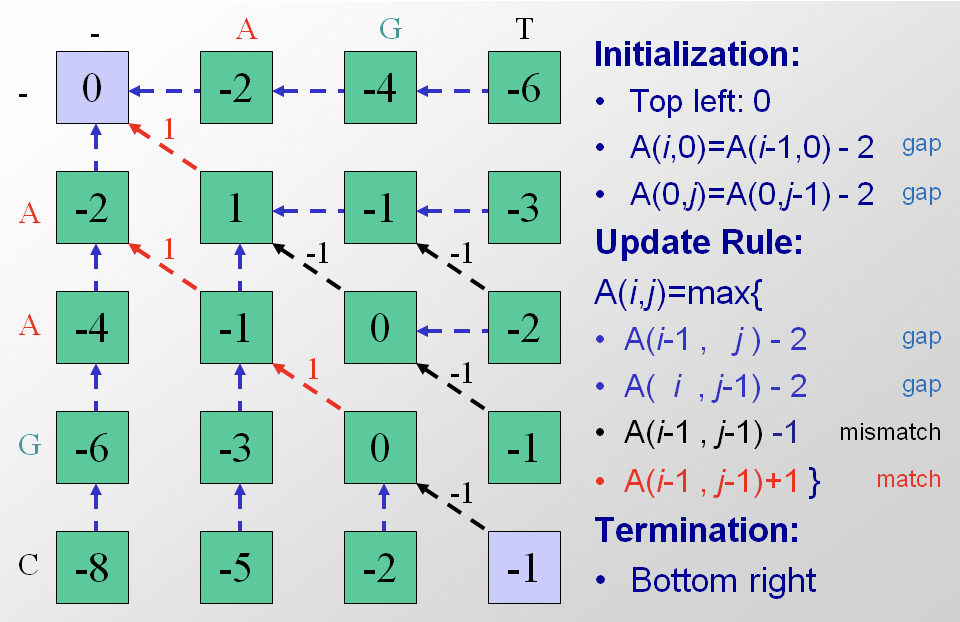
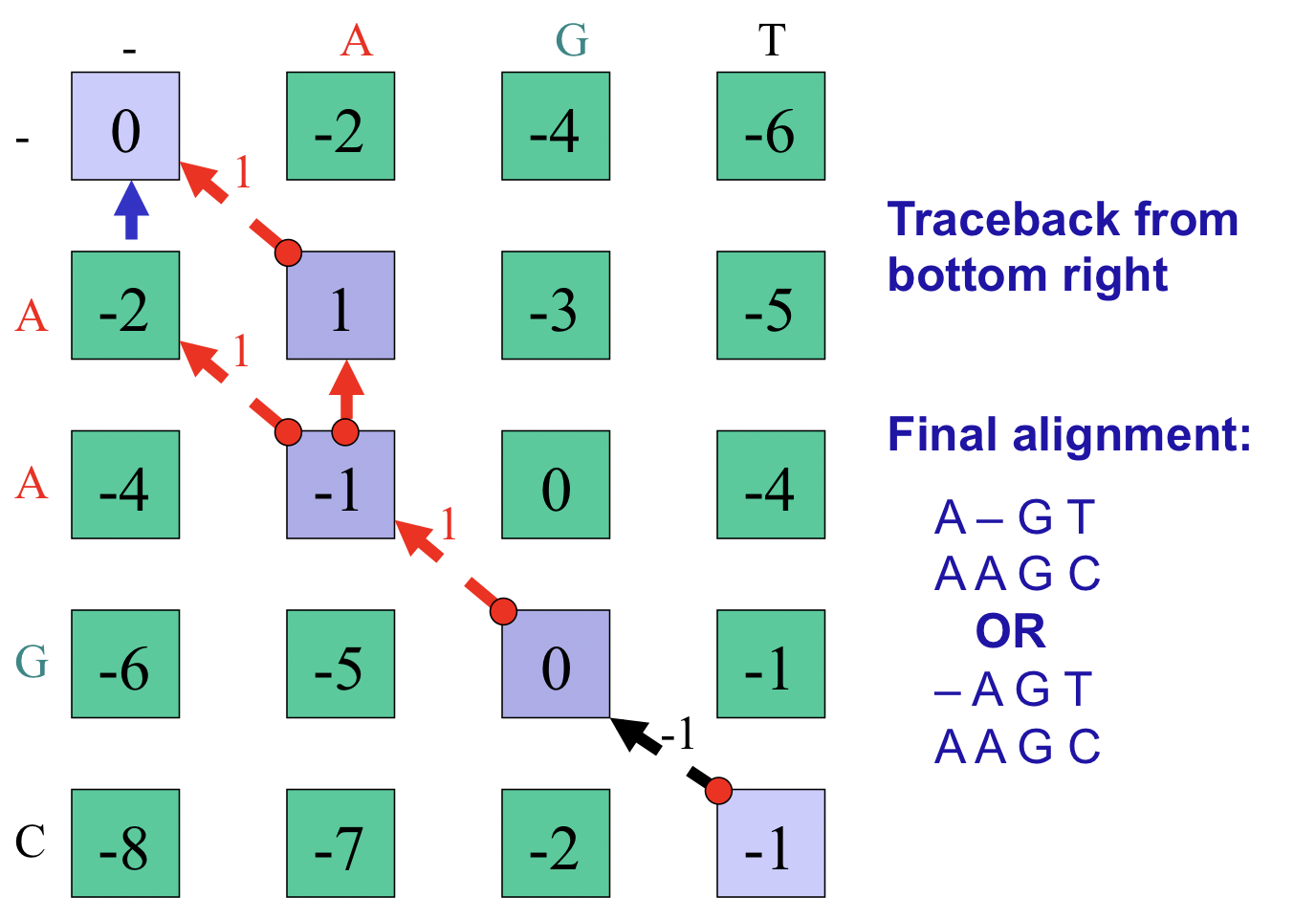
El paso final del algoritmo es la trazabilidad óptima de la ruta. En nuestro ejemplo comenzamos en la esquina inferior derecha y seguimos los punteros disponibles hasta la esquina superior izquierda. Al registrar las decisiones de alineación tomadas en cada celda durante el rastreo, podemos reconstruir la alineación de secuencia óptima de extremo a principio y luego invertirla. Obsérvese que en este caso particular existen múltiples vías óptimas (Figura 2.11). Una implementación de pseudocódigo del algoritmo Needleman-Wunsch se incluye en el Apéndice 2.11.4
Optimizaciones
El algoritmo dinámico que presentamos es mucho más rápido que la estrategia de fuerza bruta de enumerar alineaciones y funciona bien para secuencias de hasta 10 kilobases de longitud. Sin embargo, a la escala de alineaciones del genoma completo el algoritmo dado no es factible. Para alinear secuencias mucho más grandes podemos hacer modificaciones al algoritmo y mejorar aún más su rendimiento.
Programación dinámica acotada
Una posible optimización es ignorar las alineaciones de mandrinado leve (MBAs) o las alineaciones que tienen demasiados huecos. Explícitamente, podemos limitarnos a quedarnos a cierta distancia W de la diagonal en la matriz
F de subproblemas. Es decir, suponemos que la ruta de optimización en F de\(F_{0,0} \) a\( F_{m,n} \) está dentro de la distancia W a lo largo de la diagonal. Esto significa que la recursión (2.2) solo necesita aplicarse a las entradas en F dentro de la distancia W alrededor de la diagonal, y esto produce un costo de tiempo/espacio de\(O((m + n)W )\) (consulte la Figura 2.12).
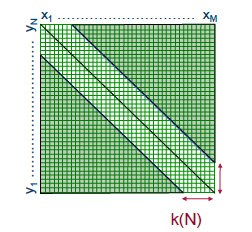
Figura 2.12: Ejemplo de programación dinámica acotada
Tenga en cuenta, sin embargo, que esta estrategia es heurística y ya no garantiza una alineación óptima. En cambio, alcanza un límite inferior sobre la puntuación óptima. Esto se puede utilizar en un paso posterior donde descartamos las recursiones en la matriz F que, dado el límite inferior, no puede conducir a una alineación óptima.
Alineación lineal de espacios
La recursión (2.2) se puede resolver usando solo espacio lineal: actualizamos las columnas en F de izquierda a derecha durante las cuales solo realizamos un seguimiento de la última columna actualizada que cuesta\(O(m)\) espacio. Sin embargo, además\(F_{m,n}\) de la puntuación de la alineación óptima, también queremos calcular una alineación correspondiente. Si usamos trace back, entonces necesitamos almacenar punteros para cada una de las entradas en F, y esto cuesta\(O(mn)\) espacio.
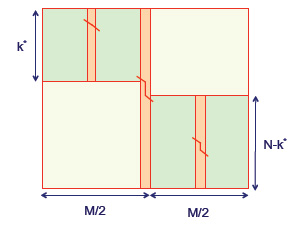
Figura 2.13: Recuperando el alineamiento de secuencia con\(O(m + n)\) el espacio
¡También es posible encontrar una alineación óptima usando solo espacio lineal! El objetivo es usar dividir y conquistar para calcular la estructura de la alineación óptima para una entrada de matriz en cada paso. La Figura 2.13 ilustra el proceso. La idea clave es que una alineación dinámica de programación pueda proceder con la misma facilidad en la dirección inversa, comenzando en la esquina inferior derecha y terminando en la parte superior izquierda. Entonces, si la matriz se divide por la mitad, entonces tanto un pase directo como un paso inverso pueden correr al mismo tiempo y converger en la columna media. En el punto de cruce podemos sumar las dos puntuaciones de alineación juntas; la celda en la columna media con la puntuación máxima debe caer en el camino óptimo general.
Podemos describir este proceso de manera más formal y cuantitativa. Primero calcula el índice de fila\(u ∈ {1,...,m}\) que está en la ruta óptima mientras cruza la\( \frac{n}{2} th\) columna. For\(1 ≤ i ≤ m \) y\(n ≤ j ≤ n\) let\(C_{i,j}\) denotar el índice de fila que está en el camino óptimo\(F_{i,j}\) al cruzar la\( \frac{n}{2} th\) columna. Después, mientras actualizamos las columnas de F de izquierda a derecha, también podemos actualizar las columnas de C de izquierda a derecha. Entonces, en\(O(mn)\) tiempo y\(O(m) \) espacio somos capaces de calcular la puntuación\(F_{m,n}\) y también\(C_{m,n}\), que es igual al índice de fila\( u ∈ {1, . . . , m}\) que está en el camino óptimo al cruzar la\( \frac{n}{2} th\) columna. Ahora entra en juego la idea de dividir y conquistar. Repetimos el procedimiento anterior para la\(u \times \frac{n}{2} \) submatriz superior izquierda de F y también repetimos el procedimiento anterior para la\( (m-u) \times \frac{n}{2} \) submatriz inferior derecha de F. Esto se puede hacer usando el espacio lineal\( O(m + n) \) asignado. El tiempo de ejecución para la submatriz superior izquierda es\( O\left(\frac{u n}{2}\right) \) y el tiempo de ejecución para la submatriz inferior derecha es\(O\left(\frac{(m-u) n}{2}\right)\), lo que sumado da un tiempo de ejecución de\( O\left(\frac{m n}{2}\right)=O(m n)\).
Seguimos repitiendo el procedimiento anterior para submatrices cada vez más pequeñas de F mientras recolectamos más y más entradas de una alineación con puntaje óptimo. El tiempo total de ejecución es\( O(m n)+O\left(\frac{m n}{2}\right)+O\left(\frac{m n}{4}\right)+\ldots=O(2mn) = O(mn)\). Entonces, sin sacrificar el tiempo de funcionamiento general (hasta un factor constante), dividir y conquistar conduce a una solución espacial lineal (ver también la Sección?? en la Conferencia 3).