2.4: Programación dinámica
- Page ID
- 54702
Antes de proceder a una solución del problema de alineación de secuencias, primero discutimos la programación dinámica, un método general y poderoso para resolver problemas con ciertos tipos de estructura.
Teoría de la Programación Dinámica
La programación dinámica se puede utilizar para resolver problemas con:
- Subestructura Óptima: La solución óptima a una instancia del problema contiene soluciones óptimas a los subproblemas.
- Subproblemas superpuestos: Hay un número limitado de subproblemas, muchos/la mayoría de los cuales se repiten muchas veces.
La programación dinámica suele utilizarse, pero no siempre, para resolver problemas de optimización, similar a los algoritmos codiciosos. A diferencia de los algoritmos codiciosos, que requieren que una propiedad de elección codiciosa sea válida, la programación dinámica funciona en una variedad de problemas en los que las elecciones localmente óptimas no producen resultados óptimos a nivel mundial. El Apéndice 2.11.3 analiza con más detalle la distinción entre algoritmos codiciosos y programación dinámica; en términos generales, los algoritmos codiciosos resuelven una clase de problemas más pequeña que la programación dinámica.
En la práctica, resolver un problema usando programación dinámica implica dos partes principales: Configurar la programación dinámica y luego realizar cómputos. La configuración de la programación dinámica suele requerir los siguientes 5 pasos:
- Encontrar una parametrización 'matricial' del problema. Determinar el número de dimensiones (variables).
- Asegurar que el espacio subproblemático sea polinomio (no exponencial). Tenga en cuenta que si se usa una pequeña porción de subproblemas, entonces la memorización puede ser mejor; de manera similar, si la reutilización de subproblemas no es extensa, la programación dinámica puede no ser la mejor solución para el problema.
- Determinar un orden transversal efectivo. Los subproblemas deben estar listos (resueltos) cuando sean necesarios, por lo que el orden de cómputos importa.
4. Determinar una fórmula recursiva: Un problema mayor generalmente se resuelve en función de sus subpartes.
5. Recuerde opciones: Por lo general, la fórmula recursiva implica un paso de minimización o maximización. Además, a menudo se necesita una representación para almacenar punteros transversales, y la representación debe ser polinómica.
Una vez que se configura la programación dinámica, el cálculo suele ser sencillo:
1. Completar sistemáticamente la tabla de resultados (y generalmente los punteros de seguimiento) y encontrar una puntuación óptima.
2. Trazback desde la puntuación óptima a través de los punteros para determinar una solución óptima.
Números de Fibonacci
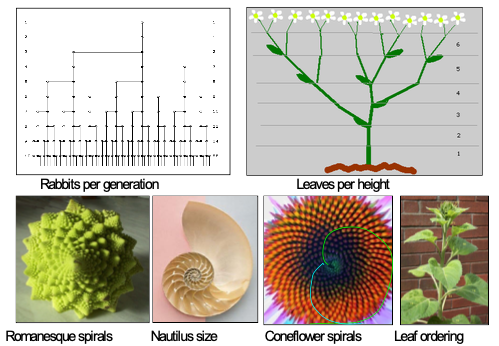
Figura 2.7: Los ejemplos de números de Fibonacci en la naturaleza son ubicuos.
Los números de Fibonacci proporcionan un ejemplo instructivo de los beneficios de la programación dinámica. La secuencia de Fibonacci se define recursivamente como F0 = F1 = 1, Fn = Fn−1 + Fn−2 para n ≤ 2. Desarrollamos un algoritmo para calcular el número n de Fibonacci, y luego refinarlo primero usando memoización y luego usando programación dinámica para ilustrar conceptos clave.
La Solución Na ̈ıve
El enfoque simple de arriba hacia abajo es simplemente aplicar la definición recursiva. El Listado 1 muestra una implementación simple de Python.

Pero este algoritmo de arriba hacia abajo se ejecuta en tiempo exponencial. Es decir, si T (n) es el tiempo que lleva computar el n º número de Fibonacci, tenemos ese\(T(n)=T(n-1)+T(n-2)+O(1), \text { so } T(n)=O\left(\phi^{n}\right)\) 9. El problema es que estamos repitiendo el trabajo resolviendo el mismo subproblema muchas veces.
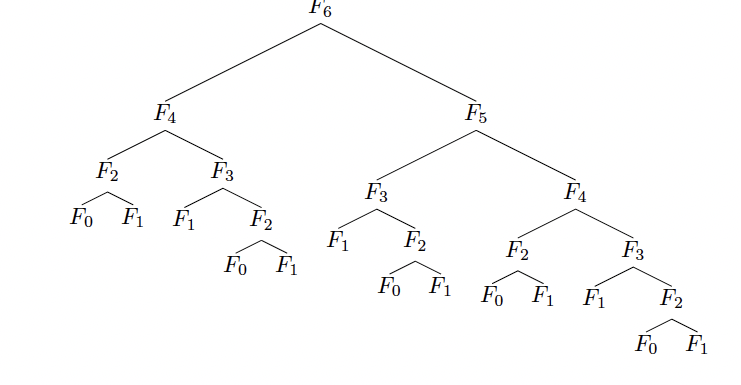
La solución de memorización
Una mejor solución que todavía utiliza el enfoque de arriba hacia abajo es memoizar las respuestas a los subproblemas. El Listado 2 da una implementación de Python que usa memorización.

Tenga en cuenta que esta implementación ahora se ejecuta en T (n) = O (n) tiempo porque cada subproblema se calcula como máximo una vez.
La solución de programación dinámica
Para calcular el nésimo número de Fibonacci, en lugar de comenzar con F (n) y usar recursión, podemos iniciar el cálculo desde abajo ya que sabemos que vamos a necesitar todos los subproblemas de todos modos. De esta manera, omitiremos gran parte del trabajo repetido que haría el enfoque de arriba hacia abajo na ̈ıve, y podremos calcular el nésimo número de Fibonacci en O (n) tiempo.
Como ejercicio formal, podemos aplicar los pasos señalados en la sección 2.4.1:
- Encuentra una parametrización 'matricial': En este caso, la matriz es unidimensional; solo hay una
a cualquier subproblema F (x).
- Asegúrese de que el espacio del subproblema sea polinomio: Dado que solo hay n − 1 subproblemas, el espacio es
polinomio.
- Determinar un orden transversal efectivo: Como se mencionó anteriormente, aplicaremos un orden transversal de abajo hacia arriba (es decir, computar los subproblemas en orden ascendente).
- Determine una fórmula recursiva: Esta es simplemente la conocida recurrencia F (n) = F (n−1) +F (n−2).
- Recordar elecciones: En este caso no hay nada que recordar, ya que no se tomaron decisiones en la fórmula recursiva.
El Listado 3 muestra una implementación de Python de este enfoque.
Este método está optimizado para usar solo espacio constante en lugar de una tabla completa ya que solo necesitamos la respuesta a cada subproblema una vez. Pero en general las soluciones de programación dinámica, queremos almacenar las soluciones a los subproblemas en una tabla ya que es posible que necesitemos utilizarlas varias veces sin volver a calcular sus respuestas. Dichas soluciones se parecerían algo a la solución de memorización en el Listado 2, pero generalmente serán de abajo hacia arriba en lugar de de arriba hacia abajo. En este ejemplo particular, la distinción entre la solución de memorización y la solución de programación dinámica es mínima ya que ambos enfoques calculan todas las soluciones de subproblemas y las utilizan el mismo número de veces. En general, la memorización es útil cuando no se computarán todos los subproblemas, mientras que la programación dinámica guarda la sobrecarga de las llamadas a funciones recursivas, y por lo tanto es preferible cuando todas las soluciones de subproblemas deben calcularse 10. Se pueden encontrar ejemplos adicionales de programación dinámica en línea [7].
Alineación de Secuencias mediante Programación Dinámica
Ahora estamos listos para resolver el problema más difícil de la alineación de secuencias mediante programación dinámica, la cual se presenta en profundidad en la siguiente sección. Tenga en cuenta que la visión clave para resolver el problema de alineación de secuencias es que las puntuaciones de alineación son aditivas. Esto nos permite crear una matriz M indexada por i y j, que son posiciones en dos secuencias S y T a alinear. La mejor alineación de S y T corresponde con la mejor trayectoria a través de la matriz M después de rellenarla usando una fórmula recursiva.
Mediante el uso de programación dinámica para resolver el problema de alineación de secuencias, logramos una solución demostrablemente óptima, que es mucho más eficiente que la enumeración de fuerza bruta.
9 φ es la proporción áurea, i.e.\(\frac{1+\sqrt{5}}{2}\)
10 En algunos casos, la programación dinámica es prácticamente la única solución aceptable; este es el caso en particular cuando las cadenas de dependencia entre subproblemas son largas: en este caso, la solución basada en memorización recurre demasiado profundamente y provoca un desbordamiento de pila

