8.1: Revisión de la conferencia anterior

Introducción a los modelos ocultos de Markov

En la última conferencia, nos familiarizamos con el concepto de cadenas de Markov de tiempo discreto y Modelos Ocultos de Markov (HMM). En particular, una cadena de Markov es un proceso aleatorio discreto que se ajusta a la propiedad de Markov, es decir, que la probabilidad del siguiente estado depende únicamente del estado actual; esta propiedad también se denomina frecuentemente “falta de memoria”. Para modelar cómo los estados cambian de paso a paso, la cadena de Markov utiliza una matriz de probabilidades de transición. Además, se caracteriza por una correspondencia uno a uno entre los estados y los símbolos observados; es decir, el estado determina completamente todos los observables relevantes. De manera más formal, una cadena de Markov está completamente definida por las siguientes variables:

• π _i ∈ Q, el estado en el ^i-ésimo paso en una secuencia de estados finitos Q de longitud N que puede contener un valor de un alfabeto finito σ de longitud K

• a _jk, la probabilidad de transición de pasar del estado j al estado k, P (π _i = k|π _i−1 = j), para cada j, k en Q

• a _0j ∈ P, la probabilidad de que el estado inicial sea j

Los ejemplos de cadenas de Markov abundan en la vida cotidiana. En la última conferencia, consideramos el ejemplo canónico de un sistema meteorológico en el que cada estado es lluvia, nieve, sol o nubes y los observables del sistema corresponden exactamente al estado subyacente: no hay nada que desconozcamos al hacer una observación, como la observación, es decir, si es soleado o lloviendo, determina completamente el estado subyacente, es decir, si está soleado o lloviendo. Supongamos, sin embargo, que estamos considerando el clima ya que está determinado probabilísticamente por las estaciones -por ejemplo, nieva más a menudo en invierno que en primavera- y supongamos además que estamos en la antigüedad y aún no tuvimos acceso al conocimiento sobre cuál es la temporada actual. Consideremos ahora el problema de tratar de inferir la temporada (el estado oculto) del clima (lo observable). Existe alguna relación entre temporada y clima tal que podemos usar información sobre el clima para hacer inferencias sobre qué estación es (si nieva mucho, probablemente no sea verano); esta es la tarea que los HMM buscan emprender. Así, en esta situación, los estados, las estaciones, se consideran “ocultos” y ya no comparten una correspondencia uno a uno con los observables, el clima. Este tipo de situaciones requieren una generalización de las cadenas de Markov conocidas como Modelos Ocultos de Markov (HMM).

¿Sabías?

Las cadenas de Markov pueden ser consideradas como WYSIWYG - Lo que ves es lo que obtienes

Los HMM incorporan elementos adicionales para modelar la desconexión entre los observables de un sistema y los estados ocultos. Para una secuencia de longitud N, cada estado observable es reemplazado por un estado oculto (la temporada) y un carácter emitido desde ese estado (el clima). Es importante señalar que los caracteres de cada estado se emiten de acuerdo a una serie de probabilidades de emisión (digamos que hay un 50% de probabilidad de nieve, 30% de probabilidad de sol y 20% de probabilidad de lluvia durante el invierno). Más formalmente, los dos descriptores adicionales de un HMM son:

• x _i ∈ X, la emisión en el paso ⁱ en una secuencia de caracteres finitos X de longitud N que puede contener un carácter de un conjunto finito de símbolos de observación v _l ∈ V
• e _k (v _l) ∈ E, la probabilidad de emisión de emitir carácter vl cuando el estado es k, P (x _i = v _l |π _i = k) En resumen, un HMM se define por las siguientes variables:

• a _jk, e _k (v _l) y a _0j que modelan el proceso aleatorio discreto
• π _i, la secuencia de estados ocultos
• x _i, la secuencia de emisiones observadas

Aplicaciones genómicas de los HMM

La siguiente figura muestra algunas aplicaciones genómicas de los HMM

Figura 8.1: Aplicaciones genómicas de los HMM

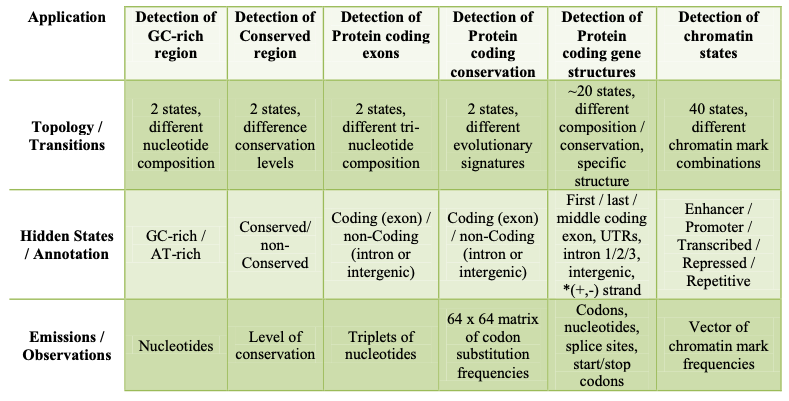
Las sutilezas de algunas de las aplicaciones que se muestran en la figura 8.1 incluyen:

• Detección de conservación de codificación de proteínas
Esto es similar a la aplicación de detectar exones codificantes de proteínas porque las emisiones tampoco son nucleótidos sino diferentes en el sentido de que, en lugar de emitir codones, se emiten frecuencias de sustitución de los codones.

• Detección de estructuras génicas codificantes de proteínas
Aquí, es importante que diferentes estados modele los exones primero, último y medio de forma independiente, porque tienen distintas características estructurales relevantes: por ejemplo, el primer exón en una transcripción pasa por un codón de inicio, el último exón pasa por un codón de parada, etc., y para hacer las mejores predicciones, nuestro modelo debe codificar estas características. Esto difiere de la aplicación de detección de exones codificantes de proteínas porque en este caso, la posición del exón no es importante.
También es importante diferenciar entre los intrones 1,2 y 3 para que pueda recordarse el marco de lectura entre un exón y el siguiente exón, por ejemplo, si un exón se detiene en la posición del segundo codón, el siguiente tiene que comenzar en la posición del tercer codón. Por lo tanto, los estados intrónicos adicionales codifican la posición del codón.

• Detección de estados de cromatina Los modelos de estado de
cromatina son dinámicos y varían de un tipo de celda a otro por lo que cada tipo de celda tendrá su propia anotación. Serán discutidos con más detalle en la conferencia de genómica incluyendo estrategias para apilar/concatenar tipos de células.

Descodificación Viterbi

Anteriormente, demostramos que cuando se le daba un HMM completo (Q, A, X, E, P), la probabilidad de que el proceso aleatorio discreto produjera la serie proporcionada de estados ocultos y emisiones viene dada por:

\[P\left(x_{1}, \ldots, x_{N}, \pi_{1}, \ldots, \pi_{N}\right)=a_{0 \pi_{i}} \prod_{i} e_{\pi_{i}}\left(x_{i}\right) a_{\pi_{i} \pi_{i+1}}\]

Esto corresponde a la probabilidad conjunta total, P (x, π). Por lo general, sin embargo, los estados ocultos no se dan y deben inferirse; no nos interesa conocer la probabilidad de la secuencia observada dado un modelo subyacente de estados ocultos, sino que queremos que la secuencia observada inferya los estados ocultos, como cuando usamos la secuencia genómica de un organismo para inferir la ubicación de sus genes. Una solución a este problema de decodificación se conoce como el algoritmo de decodificación de Viterbi. Corriendo en O (K ² N) tiempo y O (KN) espacio, donde K es el número de estados y N es la longitud de la secuencia observada, este algoritmo determina la secuencia de estados ocultos (la ruta π ^∗) que maximiza la probabilidad conjunta de los observables y estados, es decir, P (x, π). Esencialmente, este algoritmo define V _k (i) como la probabilidad de que la ruta más probable termine en el estado π _i = k, y utiliza el argumento de subestructura óptima que vimos en el módulo de alineación de secuencias del curso para calcular recursivamente V _k (i) = e _k (xi) × max _j (V _j (i − 1) a _jk) en un algoritmo de programación dinámica.

Algoritmo delantero

Volviendo por un momento al problema de 'puntuar' en lugar de 'decodificar', otro problema que podríamos querer abordar es el de, en lugar de calcular la probabilidad de que una sola ruta de estado oculto emita la secuencia observada, calcular la probabilidad total de que la secuencia sea producida por todos los posibles caminos. Por ejemplo, en el ejemplo del casino, si la secuencia de rollos es lo suficientemente larga, la probabilidad de cualquier secuencia observada y trayectoria subyacente es muy baja, incluso si es la combinación única secuencia-trayectoria más probable. En cambio, podemos querer tomar una actitud agnóstica hacia el camino y evaluar la probabilidad total de que la secuencia observada surja de alguna manera.

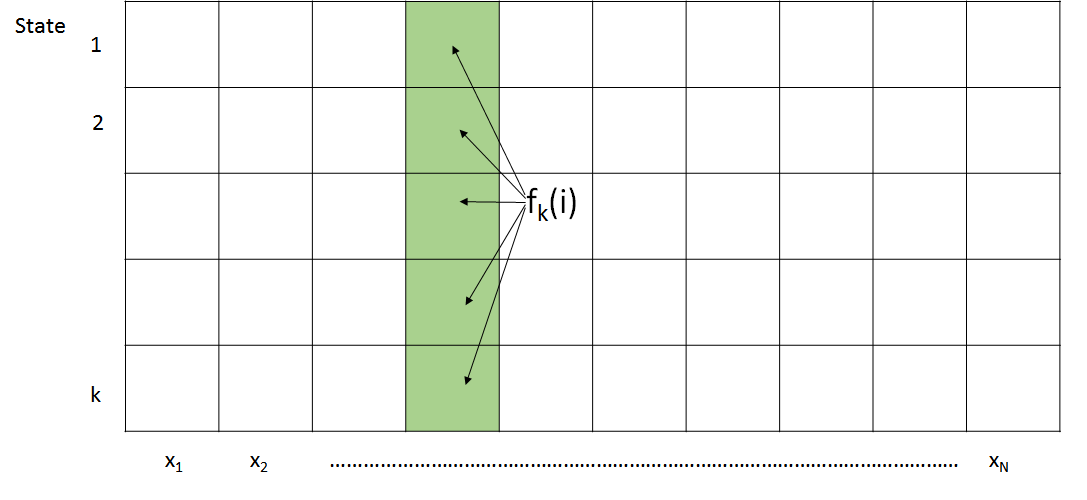
Para ello, propusimos el algoritmo Forward, que se describe en la Figura 8.2

Figura 8.2: El Algoritmo Forward

\ [\ begin {ecuación}
\ begin {array} {l}
\ text {Entrada:} x=x_ {1}\ ldots x_ {N}\\
\ text {Inicialización:}\\
\ qquad f_ {0} (0) =1, f_ {k} (0) =0,\ quad\ text {para todos} k>0\
\ text {Iteración:}\\
\ qquad f_ {k} (i) =e_ {k}\ izquierda (x_ {i} \ derecha)\ veces\ suma_ {j} a_ {j k} f_ {j} (i-1)
\ end {array}
\ end {ecuación}\ nonumber\]

\ [\ text {Terminación:}\\\ comenzar {ecuación}
P\ izquierda (x,\ pi^ {*}\ derecha) =\ suma_ {k} f_ {k} (N)
\ final {ecuación}\ nonumber\]

El algoritmo forward calcula primero la probabilidad conjunta de observar los primeros t caracteres emitidos y estar en estado k en el tiempo t. Más formalmente,
\ [\ begin {ecuación}
f_ {k} (t) =P\ left (\ pi_ {t} =k, x_ {1},\ ldots, x_ {t}\ right)
\ end {ecuación}\]

Dado que el número de caminos es exponencial en t, se debe emplear programación dinámica para resolver este problema. Podemos desarrollar una recursión simple para el algoritmo forward empleando la propiedad Markov de la siguiente manera:

\ [\ begin {ecuación}
f_ {k} (t) =\ suma_ {l} P\ izquierda (x_ {1},\ ldots, x_ {t},\ pi_ {t} =k,\ pi_ {t-1} =l\ derecha) =\ suma_ {l} P\ izquierda (x_ {1},\ ldots, x_ {t-1},\ pi_ {t-1} =l\ derecha) * P\ izquierda (x_ {t},\ pi_ {t}\ mediados\ pi_ {t-1}\ derecha)
\ final {ecuación}\]

Reconociendo que el primer término corresponde a fl (t − 1) y que el segundo término puede expresarse en términos de probabilidades de transición y emisión, esto lleva a la recursión final:

\ [\ comenzar {ecuación}
f_ {k} (t) =e_ {k}\ izquierda (x_ {t}\ derecha)\ suma_ {l} f_ {l} (t-1) * a_ {l k}
\ final {ecuación}\]

Intuitivamente, se puede entender esta recursión de la siguiente manera: Cualquier ruta que esté en el estado k en el tiempo t debe haber venido de una ruta que estaba en el estado l en el tiempo t − 1. La contribución de cada uno de estos conjuntos de rutas es ponderada por el costo de la transición del estado l al estado k También es importante señalar que el algoritmo Viterbi y el algoritmo forward comparten en gran medida la misma recursión. La única diferencia entre los dos algoritmos radica en el hecho de que el algoritmo de Viterbi, que busca encontrar solo la ruta más probable, utiliza una función de maximización, mientras que el algoritmo forward, que busca encontrar la probabilidad total de la secuencia sobre todas las rutas, usa una suma.

Ahora podemos calcular f _k (t) en base a una suma ponderada de todos los resultados del algoritmo forward tabulados durante el paso de tiempo anterior. Como se muestra en la Figura 8.2, el algoritmo directo se puede implementar fácilmente en una tabla de programación dinámica KxN. La primera columna de la tabla se inicializa de acuerdo con las probabilidades de estado inicial a _i0 y el algoritmo luego procede a procesar cada columna de izquierda a derecha. Debido a que hay entradas KN y cada entrada examina un total de K otras entradas, esto lleva a O (K ² N) complejidad de tiempo y O (KN) espacio.

Para ahora calcular la probabilidad total de una secuencia de caracteres observados bajo el HMM actual, necesitamos expresar esta probabilidad en términos del algoritmo forward da de la siguiente manera:

\ [\ start {ecuación}
P\ izquierda (x_ {1},\ ldots, x_ {n}\ derecha) =\ suma_ {l} P\ izquierda (x_ {1},\ ldots, x_ {n},\ pi_ {N} =l\ derecha) =\ suma_ {l} f_ {l} (N)
\ end {ecuación}\]

De ahí que la suma de los elementos en la última columna de la tabla de programación dinámica proporciona la probabilidad total de una secuencia observada de caracteres. En la práctica, dada una secuencia suficientemente larga de caracteres emitidos, las probabilidades de avance disminuyen muy rápidamente. Para eludir los problemas asociados con el almacenamiento de pequeños números de coma flotante, se utilizan probabilidades logarítmicas en los cálculos en lugar de las probabilidades mismas. Esta alteración requiere un ligero ajuste al algoritmo y el uso de una expansión de la serie Taylor para la función exponencial.

Esta conferencia

• Esta conferencia discutirá la decodificación posterior, un algoritmo que nuevamente inferirá la secuencia de estado oculto π que maximiza una métrica diferente. En particular, encuentra el estado más probable en cada posición sobre todas las rutas posibles y lo hace usando tanto el algoritmo hacia adelante como hacia atrás.
• Posteriormente, mostraremos cómo codificar “memoria” en una cadena de Markov agregando más estados para buscar en un genoma islas CpG de dinucleótidos.
• Luego discutiremos cómo usar la estimación de parámetros de máxima probabilidad para el aprendizaje supervisado con un conjunto de datos etiquetado
• También veremos brevemente cómo usar el aprendizaje de Viterbi para la estimación no supervisada de los parámetros de un conjunto de datos sin etiquetar
• Finalmente, aprenderemos a usar la Maximización de Expectativa (EM) para la estimación no supervisada de parámetros de un conjunto de datos sin etiquetar donde el algoritmo específico para HMM se conoce como el algoritmo Bau-Welch.