8.2: Decodificación posterior
- Page ID
- 54718
Motivación
Aunque el algoritmo de decodificación de Viterbi proporciona un medio para estimar los estados ocultos subyacentes a una secuencia de caracteres observados, otro medio válido de inferencia es proporcionado por la decodificación posterior.
La decodificación posterior proporciona el estado más probable en cualquier momento. Para ganar algo de intuición para la decodificación posterior, veamos cómo se aplica a la situación en la que un casino deshonesto alterna entre un dado justo y cargado. Supongamos que entramos al casino sabiendo que el injusto muere se usa el 60 por ciento del tiempo. Con este conocimiento y sin troqueles, nuestra mejor suposición para el dado actual es obviamente el cargado. Después de un rollo, la probabilidad de que se utilizó el dado cargado viene dada por
\ [\ begin {ecuación}
P (\ text {die} =\ text {loaded}\ mid\ text {roll} =k) =\ frac {P (\ text {die} =\ text {loaded}) * P (\ text {roll} =k\ mid\ text {die} =\ text {loaded})} {P (\ text {roll} =k)}
\ end {ecuación}\]
Si en cambio observamos una secuencia de N troqueles, ¿cómo se realiza una inferencia similar? Al permitir que la información fluya entre los N rollos e influya en la probabilidad de cada estado, la decodificación posterior es una extensión natural de la inferencia anterior a una secuencia de longitud arbitraria. De manera más formal, en lugar de identificar una sola ruta de máxima verosimilitud, la decodificación posterior considera la probabilidad de que cualquier camino se encuentre en el estado k en el tiempo t dados todos los caracteres observados, es decir, P (πt = k|x 1,... , x n). El estado que maximiza esta probabilidad para un tiempo dado se considera entonces como el estado más probable en ese momento.
Es importante señalar que además de que la información fluya hacia adelante para determinar el estado más probable en un punto, la información también puede fluir hacia atrás desde el final de la secuencia a ese estado para aumentar o reducir la probabilidad de cada estado en ese punto. Esto es en parte una consecuencia natural de la reversibilidad de la regla de Bayes: nuestras probabilidades cambian de probabilidades previas a probabilidades posteriores al observar más datos. Para dilucidar esto, imagina de nuevo el ejemplo del casino. Como se dijo anteriormente, sin observar ningún rollo, lo más probable es que el estado0 sea injusto: esta es nuestra probabilidad previa. Si el primer rollo es un 6, nuestra creencia de que state1 es injusto se refuerza (si rodar seis es más probable en un dado injusto). Si se vuelve a rodar un 6, la información fluye hacia atrás desde el segundo rollo de troqueles y refuerza aún más nuestro estado1 la creencia de un dado injusto. Cuantos más rollos tengamos, más información fluye hacia atrás y refuerza o contrasta nuestras creencias sobre el estado, ilustrando así la forma en que la información fluye hacia atrás y hacia adelante para afectar nuestra creencia sobre los estados en la Decodificación Posterior.
Usando algunas manipulaciones elementales, podemos reorganizar esta probabilidad en la siguiente forma usando la regla de Bayes:
\ [\ begin {ecuación}
\ pi_ {t} ^ {*} =\ nombreoperador {argmax} _ {k} P\ izquierda (\ pi_ {t} =k\ mid x_ {1},\ ldots, x_ {n}\ derecha) =\ nombreoperador {argmax} _ _ {k}\ frac {P\ izquierda (\ pi_ {t} =k, x_ {1},\ lpuntos, x_ {n}\ derecha)} {P\ izquierda (x_ {1},\ lpuntos, x_ {n}\ derecha)}
\ final {ecuación}\]
Debido a que P (x) es una constante, podemos descuidarla a la hora de maximizar la función. Por lo tanto,
\ [\ begin {ecuación}
\ pi_ {t} ^ {*} =\ nombreoperador {argmax} _ {k} P\ izquierda (\ pi_ {t} =k, x_ {1},\ ldots, x_ {t}\ derecha) * P\ izquierda (x_ {t+1},\ ldots, x_ {n}\ mediados\ pi_ {t} =k, _ {1},\ lpuntos, x_ {t}\ derecha)
\ final {ecuación}\]
Usando la propiedad Markov, podemos simplemente escribir esta expresión de la siguiente manera:
\ [\ begin {ecuación}
\ pi_ {t} ^ {*} =\ nombreoperador {argmax} _ {k} P\ izquierda (\ pi_ {t} =k, x_ {1},\ ldots, x_ {t}\ derecha) * P\ izquierda (x_ {t+1},\ ldots, x_ {n}\ mediados\ pi_ {t} =k derecha\) =\ nombreoperador {argmax} _ {k} f_ {k} (t) * b_ {k} (t)
\ final {ecuación}\]
Aquí, hemos definido\ (\ begin {ecuación}
f_ {k} (t) =P\ izquierda (\ pi_ {t} =k, x_ {1},\ ldots, x_ {t}\ derecha)\ text {y} b_ {k} (t) =P\ left (x_ {t+1},\ ldots, x_ {n}\ mid\ pi_ {t} =k\ derecha)
\ end {ecuación}\). Como veremos en breve, estos parámetros se calculan utilizando el algoritmo forward y el algoritmo back respectivamente. Para resolver el problema de decodificación posterior, solo necesitamos resolver cada uno de estos subproblemas. El algoritmo forward se ha ilustrado en el capítulo anterior y en la revisión al inicio de este capítulo y el algoritmo hacia atrás se explicará en la siguiente sección.
Algoritmo hacia
Como se describió anteriormente, el algoritmo hacia atrás se utiliza para calcular la siguiente probabilidad:
\ [\ comenzar {ecuación}
b_ {k} (t) =P\ izquierda (x_ {t+1},\ lpuntos, x_ {n}\ mediados\ pi_ {t} =k\ derecha)
\ final {ecuación}\]
Podemos comenzar a desarrollar una recursión n expandiéndonos a la siguiente forma:
\ [\ comenzar {ecuación}
b_ {k} (t) =\ suma_ {l} P\ izquierda (x_ {t+1},\ lpuntos, x_ {n},\ pi_ {t+1} =l\ mediados\ pi_ {t} =k\ derecha)
\ final {ecuación}\]
De la propiedad de Markov, luego obtenemos:
\ [\ begin {ecuación}
b_ {k} (t) =\ suma_ {l} P\ izquierda (x_ {t+2},\ ldots, x_ {n}\ mid\ pi_ {t+1} =l\ derecha) * P\ izquierda (\ pi_ {t+1} =l\ mid\ pi_ {t} =k\ derecha) * P\ izquierda (x_ {t+1}\ mediados\ pi_ {t+1} =k\ derecha)
\ final {ecuación}\]
El primer término simplemente corresponde a bl (t+1). Expresar en términos de probabilidades de emisión y transición da la recursión final:
\ [\ begin {ecuación}
b_ {k} (t) =\ suma_ {l} b_ {l} (i+1) * a_ {k l} * e_ {l}\ izquierda (x_ {t+1}\ derecha)
\ final {ecuación}\]
La comparación de las recursiones hacia adelante y hacia atrás conduce a una visión interesante. Mientras que el algoritmo forward usa los resultados en t − 1 para calcular el resultado para t, el algoritmo hacia atrás utiliza los resultados de t + 1, lo que lleva naturalmente a sus respectivos nombres. Otra diferencia significativa radica en las probabilidades de emisión; mientras que las emisiones para el algoritmo directo ocurren desde el estado actual y por lo tanto pueden excluirse de la suma, las emisiones para el algoritmo de retroceso ocurren en el tiempo t + 1 y por lo tanto deben incluirse dentro de la suma.
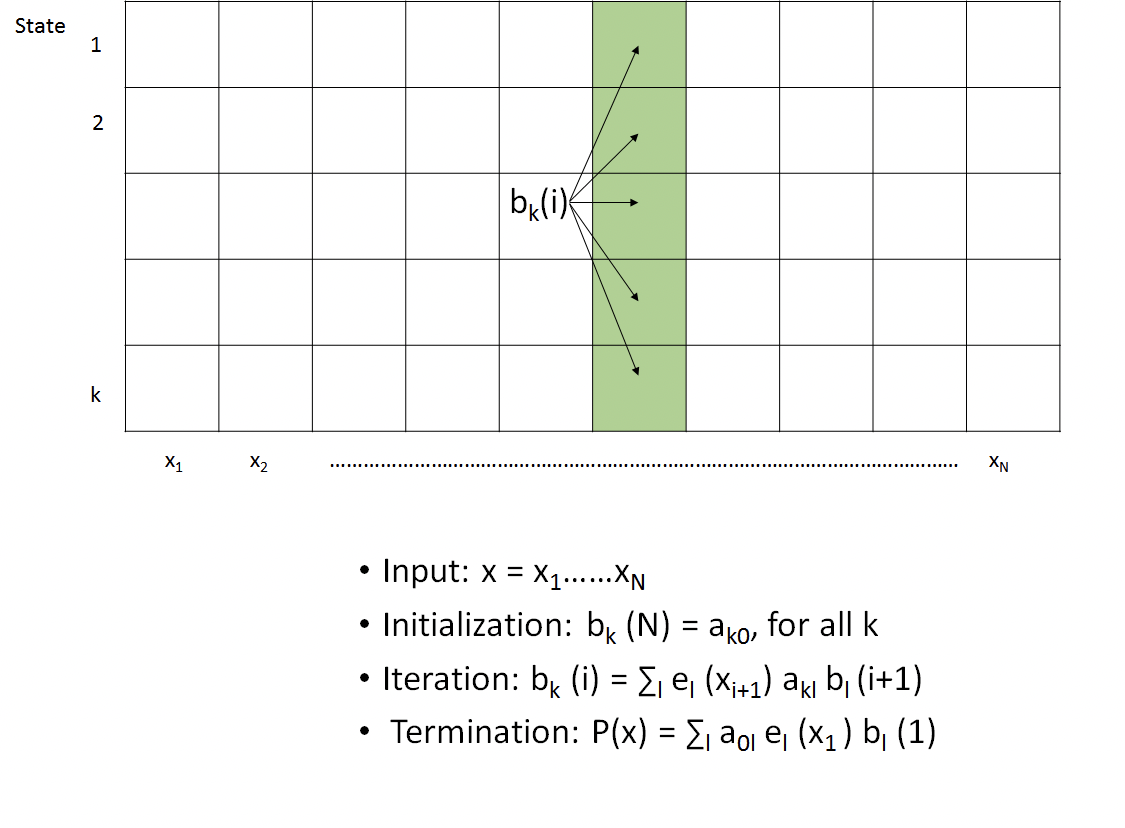
Dadas sus similitudes, no es sorprendente que el algoritmo hacia atrás también se implemente utilizando una tabla de programación dinámica KxN. El algoritmo, como se representa en la Figura 8.3, comienza inicializando la columna más a la derecha de la tabla a la unidad. Procediendo de derecha a izquierda, cada columna se calcula tomando una suma ponderada de los valores de la columna a la derecha de acuerdo con la recursión descrita anteriormente. Después de calcular la columna situada más a la izquierda, se han calculado todas las probabilidades hacia atrás y el algoritmo termina. Debido a que hay entradas KN y cada entrada examina un total de K otras entradas, esto lleva a O (K 2 N) complejidad de tiempo y O (KN) espacio, límites idénticos a los del algoritmo de avance.
Así como P (X) se calculó sumando la columna más a la derecha de la tabla DP del algoritmo directo, P (X) también se puede calcular a partir de la suma de la columna más a la izquierda de la tabla DP del algoritmo hacia atrás. Por lo tanto, estos métodos son prácticamente intercambiables para este cálculo en particular.
¿Sabías?
Tenga en cuenta que incluso cuando se ejecuta el algoritmo hacia atrás, se usan probabilidades de transición hacia adelante, es decir, si moverse en la dirección hacia atrás implica una transición desde el estado B → A, se usa la probabilidad de transición desde el estado A → B. Esto se debe a que moverse hacia atrás del estado B al estado A implica que el estado B sigue al estado A en nuestro orden normal, hacia adelante, llamando así a la misma probabilidad de transición.
El panorama general
¿Por qué tenemos que hacer cálculos tanto hacia adelante como hacia atrás para la decodificación posterior, mientras que los algoritmos que hemos discutido anteriormente requieren solo una dirección? La diferencia radica en el hecho de que la decodificación posterior busca producir probabilidades para los estados subyacentes de posiciones individuales en lugar de secuencias completas de posiciones. Al buscar encontrar el estado subyacente más probable de una posición dada, necesitamos tener en cuenta toda la secuencia en la que existe esa posición, tanto antes como después de ella, como corresponde a un enfoque bayesiano -y hacerlo en un algoritmo de programación dinámica, en el que calculamos recursivamente y terminamos con un maximizando la función, debemos acercarnos a nuestra posición de interés desde ambos lados.
Dado que podemos calcular tanto f k (t) como b k (t) en θ (K 2 N) tiempo y θ (KN) espacio para todos t = 1. n, podemos usar decodificación posterior para determinar el estado más probable π t ∗ para t = 1. n. n. La expresión relevante viene dada por
\ [\ begin {ecuación}
\ pi_ {t} ^ {*} =\ nombreoperador {argmax} _ {k} P\ left (\ pi_ {i} =k\ mid x\ right) =\ frac {f_ {k} (i) * b_ {k} (i)} {P (x)}
\ end {ecuación}\]
Con dos métodos (Viterbi y posterior) para decodificar, ¿cuál es más apropiado? Al intentar clasificar cada estado oculto, el método de decodificación Posterior es más informativo porque toma en cuenta todas las rutas posibles a la hora de determinar el estado más probable. En contraste, el método Viterbi sólo toma en cuenta una ruta, que puede terminar representando una mínima fracción de la probabilidad total. Al mismo tiempo, sin embargo, ¡la decodificación posterior puede dar una secuencia inválida de estados! Al seleccionar el estado de probabilidad máxima de cada posición de forma independiente, no estamos considerando cuán probables son las transiciones entre estos estados. Por ejemplo, los estados identificados en los puntos de tiempo t y t + 1 podrían tener una probabilidad de transición cero entre ellos. Como resultado, seleccionar un método de decodificación depende en gran medida de la aplicación de interés.
Preguntas frecuentes
P: ¿Qué implica cuando el algoritmo de Viterbi y la decodificación Posterior no están de acuerdo en el camino?
R: En cierto sentido, es simplemente un recordatorio de que nuestro modelo nos da para qué está seleccionando. Cuando buscamos el estado de probabilidad máxima de cada posición independiente y despreciamos las transiciones entre estos estados de probabilidad máxima, podemos obtener algo diferente a cuando buscamos encontrar la ruta total más probable. La biología es complicada; es importante pensar qué métrica es más relevante para la situación biológica en cuestión. En el contexto genómico, un desacuerdo podría ser el resultado de alguna biología 'funky'; empalme alternativo, por ejemplo. En algunos casos, el algoritmo de Viterbi estará cerca de la decodificación Posterior mientras que en algunos otros pueden estar en desacuerdo.


