15.3: Algoritmos de Clustering
- Page ID
- 54997
Para analizar los datos de expresión génica, es común realizar análisis de agrupamiento. Existen dos tipos de algoritmos de agrupamiento: particionamiento y aglomerativo. La agrupación particional divide los objetos en clústeres no superpuestos para que cada objeto de datos esté en un subconjunto. Alternativamente, los métodos de agrupamiento aglomerativo producen un conjunto de clústeres anidados organizados como una jerarquía que representa estructuras de niveles de detalle más amplios a más finos.
Agrupación K-Means
El algoritmo k-means agrupa n objetos en función de sus atributos en k particiones. Este es un ejemplo de partición, donde cada punto se asigna a exactamente un clúster de tal manera que se minimiza la suma de distancias desde cada punto hasta su centro etiquetado correspondientemente. La motivación subyacente a este proceso es hacer los clusters más compactos posibles, generalmente en términos de una métrica de distancia euclidiana.
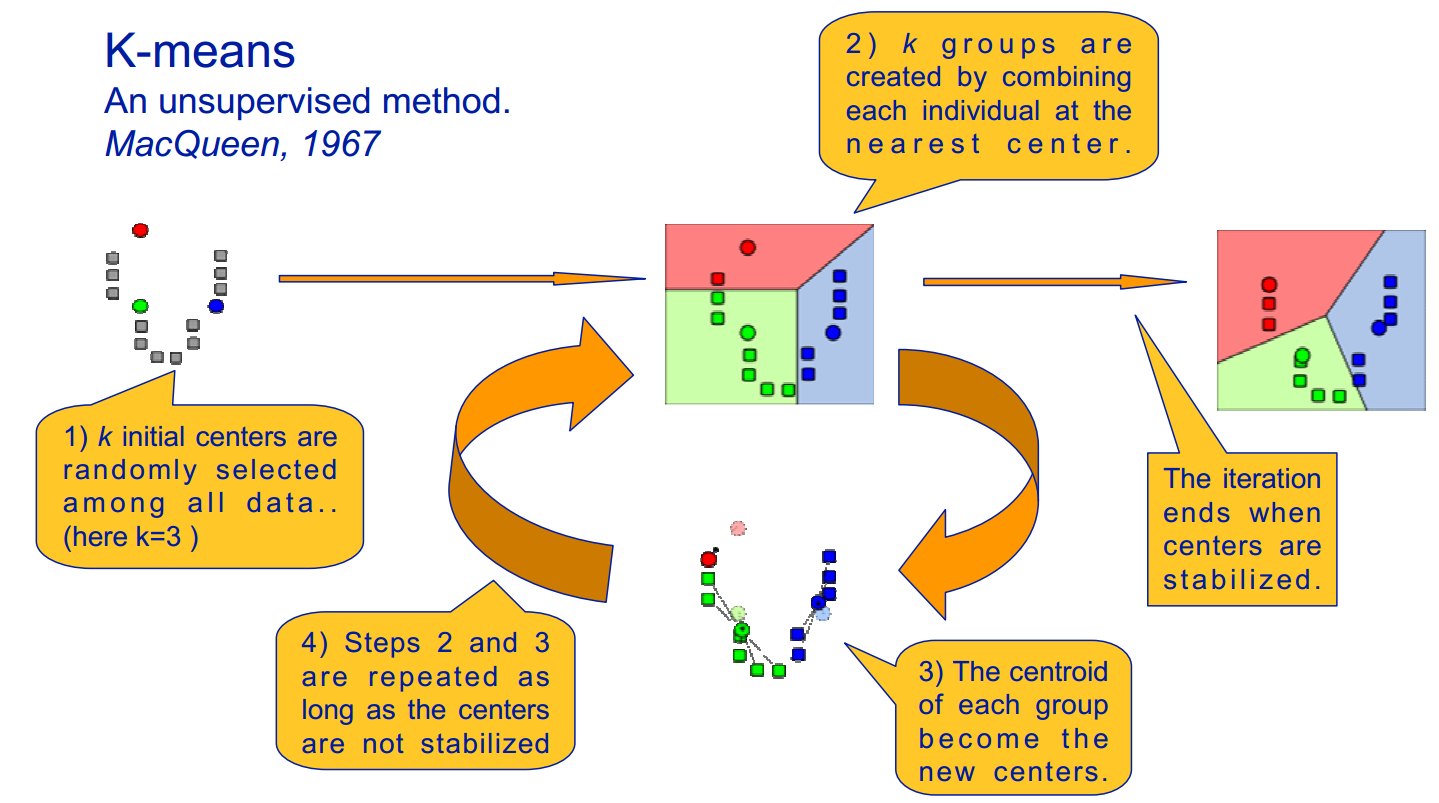
El algoritmo k-means, como se ilustra en la figura 15.8, se implementa de la siguiente manera:
- Supongamos un número fijo de clústeres, k
- Inicialización: Inicializar aleatoriamente las k medias μk asociadas a los clústeres y asignar cada punto de datos x i al clúster más cercano, donde la distancia entre x i y μ k viene dada por d i, k = (x i − μ k) 2.
- Iteración: Recalcular el centroide del clúster dados los puntos que se le asignan:\(\mu_{k}(n+1)=\sum_{x_{i} \in k} \frac{x_{i}}{\left|x^{k}\right|}\) donde x k es el número de puntos con etiqueta k. Reasignar puntos de datos a los k nuevos centroides por la métrica de distancia dada. Los nuevos centros se calculan efectivamente para ser el promedio de los puntos asignados a cada cluster.
- Terminación: Iterar hasta la convergencia o hasta que se haya alcanzado un número de iteraciones especificado por el usuario. Tenga en cuenta que la iteración puede quedar atrapada en algún óptimo local.
Existen varios métodos para elegir k: simplemente mirar los datos para identificar clústeres potenciales o intentar iterativamente valores para n, mientras penaliza la complejidad del modelo. Siempre podemos hacer mejores clústeres aumentando k, pero en algún momento comenzamos a sobreajustar los datos.
También podemos pensar en k-means como tratar de minimizar un criterio de costo asociado con el tamaño de cada clúster, donde el costo aumenta a medida que los clústeres se vuelven menos compactos. Sin embargo, algunos puntos pueden estar casi a medio camino entre dos centros, lo que no encaja bien con el agrupamiento binario que pertenece a k-means.
Agrupación difusa de K-medias
En la agrupación difusa, cada punto tiene una probabilidad de pertenecer a cada clúster, en lugar de pertenecer completamente a un solo clúster. Fuzzy k-means trata específicamente de lidiar con el problema donde los puntos están algo entre centros o de otra manera ambiguos reemplazando la distancia con la probabilidad, que por supuesto podría ser alguna función de la distancia, como tener probabilidad relativa a la inversa de la distancia. La k-media difusa usa un centroide ponderado basado en esas probabilidades. Los procesos de inicialización, iteración y terminación son los mismos que los utilizados en k-medias. Los conglomerados resultantes se analizan mejor como distribuciones probabilísticas en lugar de una asignación dura de etiquetas. Uno debería darse cuenta de que k-means es un caso especial de k-medias difusas cuando la función de probabilidad utilizada es simplemente 1 si el punto de datos está más cerca de un centroide y 0 en caso contrario.
El algoritmo difuso k-means es el siguiente:
- Asumir un número fijo de clústeres k
- Inicialización: Inicializar aleatoriamente las k medias μk asociadas a los clústeres y calcular la probabilidad de que cada punto de datos xi sea miembro de un clúster dado k, P (el punto xi tiene la etiqueta k|xi, k).
- Iteración: Recalcular el centroide del clúster como el centroide ponderado dadas las probabilidades de pertenencia a todos los puntos de datos xi:\[\mu_{k}(n+1)=\frac{\sum_{x_{i} \in k} x_{i} \times P\left(\mu_{k} \mid x_{i}\right)^{b}}{\sum_{x_{i} \in k} P\left(\mu_{k} \mid x_{i}\right)^{b}} \nonumber \] Y recalcular las membresías actualizadas P (μ k |x i) (hay diferentes formas de definir membresía, aquí hay solo un ejemplo):\[P\left(\mu_{k} \mid x_{i}\right)=\left(\sum_{j=1}^{k}\left(\frac{d_{i k}}{d_{j k}}\right)^{\frac{2}{b-1}}\right)^{-1} \nonumber \]
- Terminación: Iterar hasta que la matriz de membresía converja o hasta que se haya alcanzado un número de iteraciones especificado por el usuario (la iteración puede quedar atrapada en algunos máximos o mínimos locales)
El b aquí es el exponente de ponderación que controla los pesos relativos que se colocan en cada partición, o el grado de borrosidad. Cuando b− > 1, las particiones que minimizan la función de error cuadrado son cada vez más duras (no borrosas), mientras que como b− > ∞ todas las membresías se acercan a 1, que es el estado más difuso. No hay k evidencia teórica de cómo elegir un b óptimo, mientras que los valores empíricos útiles se encuentran entre [1, 30], y en la mayoría de los estudios, 1.5\(\leqslant \) b\(\legslant \) 3.0 funcionó bien.
K-Means como modelo generativo
Un modelo generativo es un modelo para generar aleatoriamente valores de datos observables, dados algunos parámetros ocultos. Mientras que un modelo generativo es un modelo de probabilidad de todas las variables, un modelo discriminativo proporciona un modelo condicional solo de la (s) variable (s) objetivo (s) usando las variables observadas.
Para hacer de k-medias un modelo generativo, ahora lo miramos de manera probabilística, donde asumimos que los puntos de datos en el clúster k se generan usando una distribución gaussiana con la media en el centro del clúster y una varianza de 1, lo que da
\[P\left(x_{i} \mid \mu_{k}\right)=\frac{1}{\sqrt{2 \pi}} \exp \left\{-\frac{\left(x_{i}-\mu_{k}\right)^{2}}{2}\right\}.\]
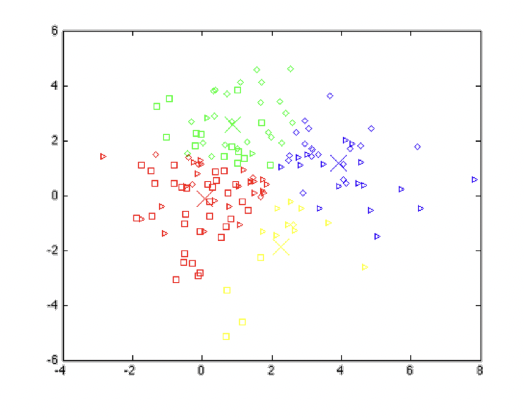
Esto da una representación estocástica de los datos, como se muestra en la figura 15.10. Ahora esto se convierte en un problema de máxima verosimilitud, que, mostraremos a continuación, es exactamente equivalente al algoritmo original de k-means mencionado anteriormente.
.png)
En el paso de generación, queremos encontrar una partición más probable, o asignación de etiqueta, para cada xi dada la media μk. Con la suposición de que cada punto se dibuja de forma independiente, podríamos buscar la etiqueta de máxima verosimilitud para cada punto por separado:
\[\arg \max _{k} P\left(x_{i} \mid \mu_{k}\right)=\arg \max _{k} \frac{1}{\sqrt{2 \pi}} \exp \left\{-\frac{\left(x_{i}-\mu_{k}\right)^{2}}{2}\right\}=\arg \min _{k}\left(x_{i}-\mu_{k}\right)^{2} \nonumber \]
Esto es totalmente equivalente a encontrar el centro de clúster más cercano en el algoritmo original de k-means.
En el paso Estimación, buscamos la estimación de máxima verosimilitud de la media del clúster μk, dadas las particiones (etiquetas):
\[ \left.\arg \max _{\mu}\left\{\log \prod_{i} P\left(x_{i} \mid \mu\right)\right\}=\arg \max _{\mu} \sum_{i}\left\{-\frac{1}{2}\left(x_{i}-\mu\right)^{2}+\log \left(\frac{1}{\sqrt{2 \pi}}\right)\right)\right\}=\arg \min _{\mu} \sum_{i}\left(x_{i}-\mu\right)^{2} \nonumber \]
Tenga en cuenta que la solución de este problema es exactamente el centroide de la x i, que es el mismo procedimiento que el algoritmo k-means original.
Desafortunadamente, dado que k-medias asume independencia entre los ejes, la covarianza y la varianza no se contabilizan usando k-medias, por lo que modelos como las distribuciones oblongas no son posibles. Sin embargo, este problema puede resolverse cuando se generaliza este problema en un problema de maximización de expectativas.
Maximización de expectativas
K-medias se puede ver como un ejemplo de EM (algoritmos de maximización de expectativas), como se muestra en la figura 15.11 donde la expectativa consiste en la estimación de etiquetas ocultas, Q, y la maximización de la probabilidad esperada ocurre dados los datos y Q. Asignando a cada punto la etiqueta del centro más cercano corresponde a la E paso de estimar la etiqueta más probable dado el parámetro anterior. Después, utilizando los datos producidos en el paso E como observación, mover el centroide al promedio de las etiquetas asignadas a ese centro corresponde al paso M de maximizar la probabilidad del centro dadas las etiquetas. Este caso es análogo al aprendizaje de Viterbi. Se puede hacer una comparación similar para k-medias difusas, que es análoga a Baum-Welch de los HMM. La Figura 15.12 compara el agrupamiento, HMM y el descubrimiento de motivos con respecto al algoritmo de minimización de expectativas.
Cabe señalar que utilizando el marco EM, el enfoque de k medias puede generalizarse a racimos de forma oblonga y tamaños variables. Con k medias, los puntos de datos siempre se asignan al centro de clúster más cercano. Al introducir una matriz de covarianza en la función de probabilidad gaussiana, podemos permitir clústeres de diferentes tamaños. Al establecer la varianza para que sea diferente a lo largo de diferentes ejes, incluso podemos crear distribuciones oblongas.
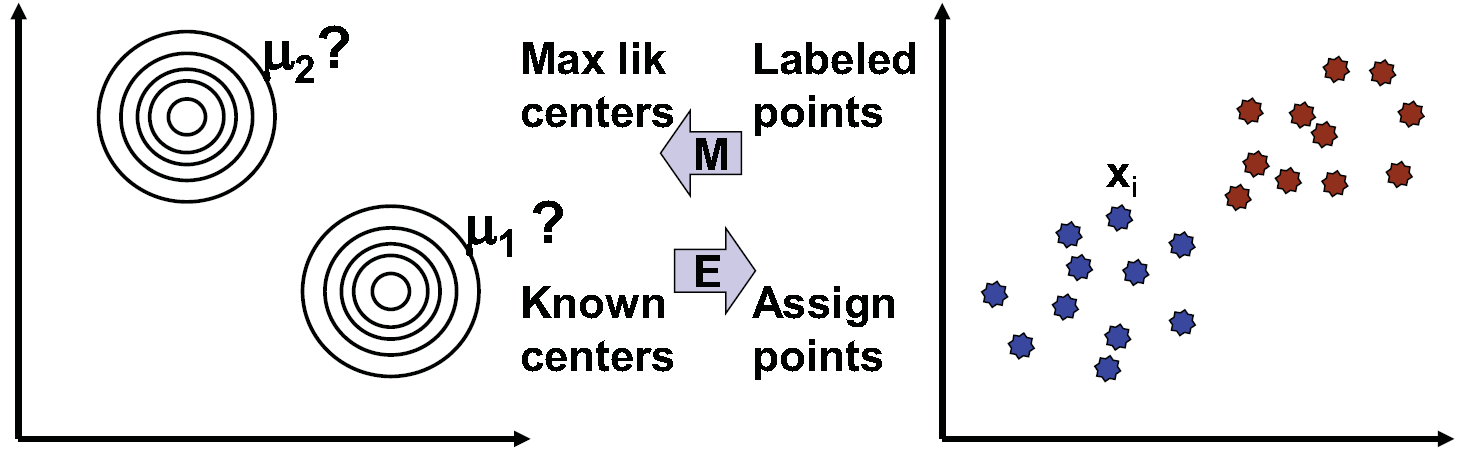
Figura 15.11: K-medias como algoritmo de maximización de expectativas (EM).
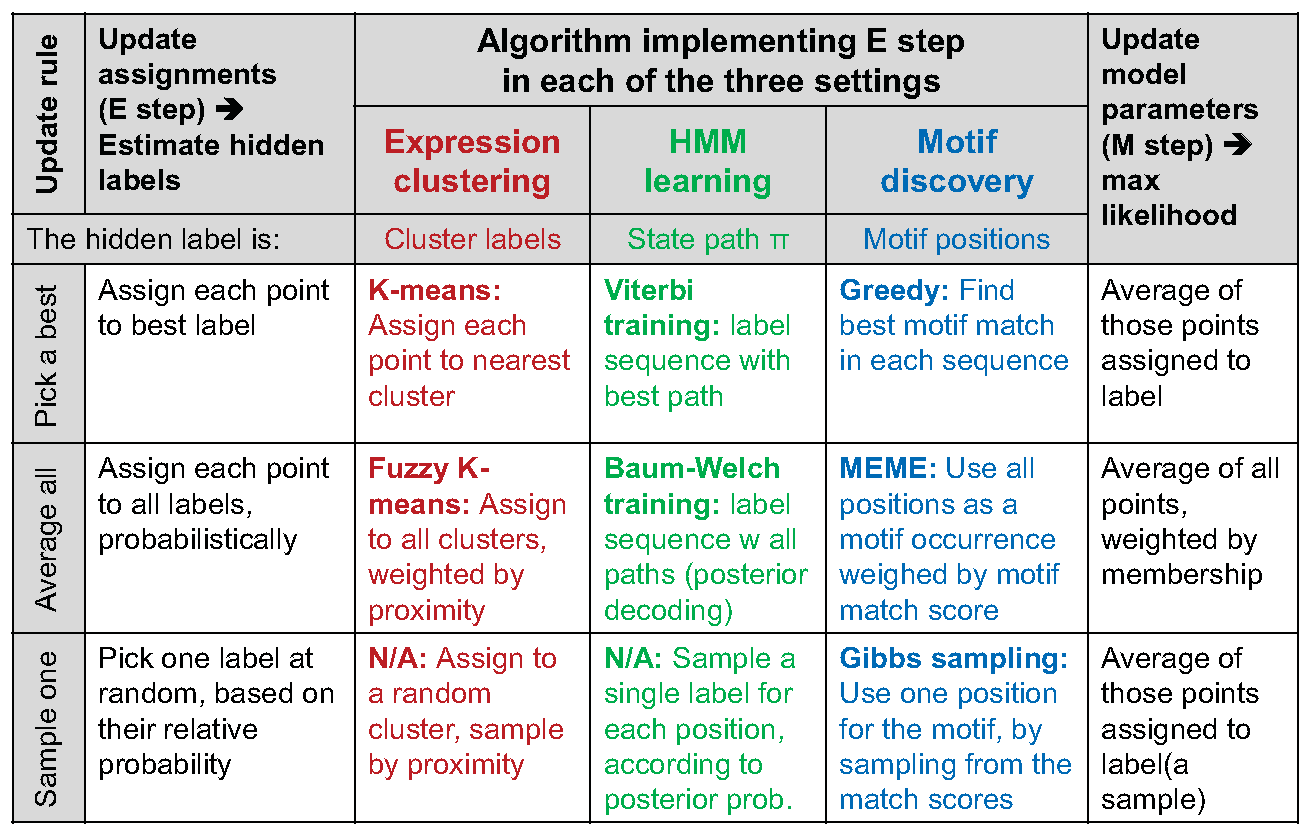
EM está garantizado para converger y garantizado para encontrar la mejor respuesta posible, al menos desde un punto de vista algorítmico. El problema notable con esta solución es que la existencia de máximos locales de densidad de probabilidad puede impedir que el algoritmo converja al máximo global. Un enfoque que puede evitar esta complicación es intentar múltiples inicializaciones para determinar mejor el panorama de probabilidades.
Las limitaciones del algoritmo K-Means
El algoritmo k-means tiene algunas limitaciones que son importantes a tener en cuenta a la hora de usarlo y antes de elegirlo. En primer lugar, requiere de una métrica. Por ejemplo, no podemos usar el algoritmo k-means en un conjunto de palabras ya que no tendríamos ninguna métrica.
La segunda limitación principal del algoritmo k-means es su sensibilidad al ruido. Una forma de tratar de reducir el ruido es ejecutar un análisis de componentes principales de antemano. Otra forma es ponderar cada variable para dar menos peso a las variables afectadas por el ruido significativo: los pesos se calcularán dinámicamente en cada iteración del algoritmo K-medias [3].
La tercera limitación es que la elección de los centros iniciales puede influir en los resultados. Existen heurísticas para seleccionar los centros de clúster iniciales, pero ninguno de ellos es perfecto.
Por último, necesitamos conocer a priori el número de clases. Como hemos visto, hay formas de sortear este problema, esencialmente ejecutando varias veces el algoritmo variando k o usando la regla general\ (k\ approx\ sqrt {n/2} si nos falta en el lado computacional. es.wikipedia.org/wiki/Determining_ the_number_of_clusters_in_data_set resume bien el diferentes técnicas para seleccionar el número de clústeres. La agrupación jerárquica proporciona un enfoque práctico para elegir el número de clústeres.
Clustering jerárquico
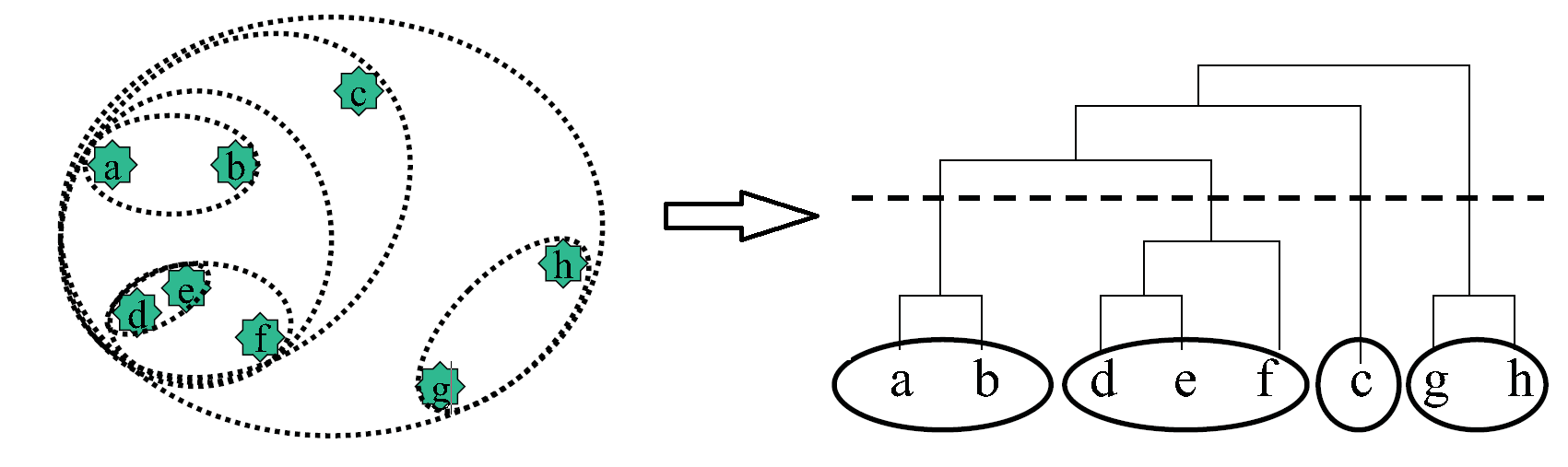
Si bien la agrupación discutida hasta ahora a menudo proporciona información valiosa sobre la naturaleza de varios datos, generalmente pasan por alto un componente esencial de los datos biológicos, a saber, la idea de que la similitud podría existir en múltiples niveles. Para ser más precisos, la similitud es una propiedad intrínsecamente jerárquica, y este aspecto no se aborda en los algoritmos de agrupamiento discutidos hasta ahora. La agrupación jerárquica aborda específicamente esto de una manera muy simple, y es quizás el algoritmo más utilizado para los datos de expresión. Como se ilustra en la figura 15.13, se implementa de la siguiente manera:
1. Inicialización: Inicializar una lista que contenga cada punto como un clúster independiente.
2. Iteración: Cree un nuevo clúster que contenga los dos clústeres más cercanos de la lista. Agregar este nuevo clúster a
la lista y eliminar los dos grupos constitutivos de la lista.
Un beneficio clave de usar clústeres jerárquicos y hacer un seguimiento de los tiempos en los que fusionamos ciertos clústeres es que podemos crear una estructura de árbol que detalla los momentos en que nos unimos a cada clúster, como se puede ver en la figura 15.13. Así, para obtener una serie de clusters que se ajuste a tu problema, simplemente cortas a un nivel de corte de tu elección como en la figura 15.13 y eso te da el número de racimos correspondientes a ese nivel de corte. No obstante, tenga en cuenta que un escollo potencial con este enfoque es que en ciertos niveles de corte, los elementos que están bastante cerca en el espacio (como e y b en la figura 15.13), podrían no estar en el mismo clúster.
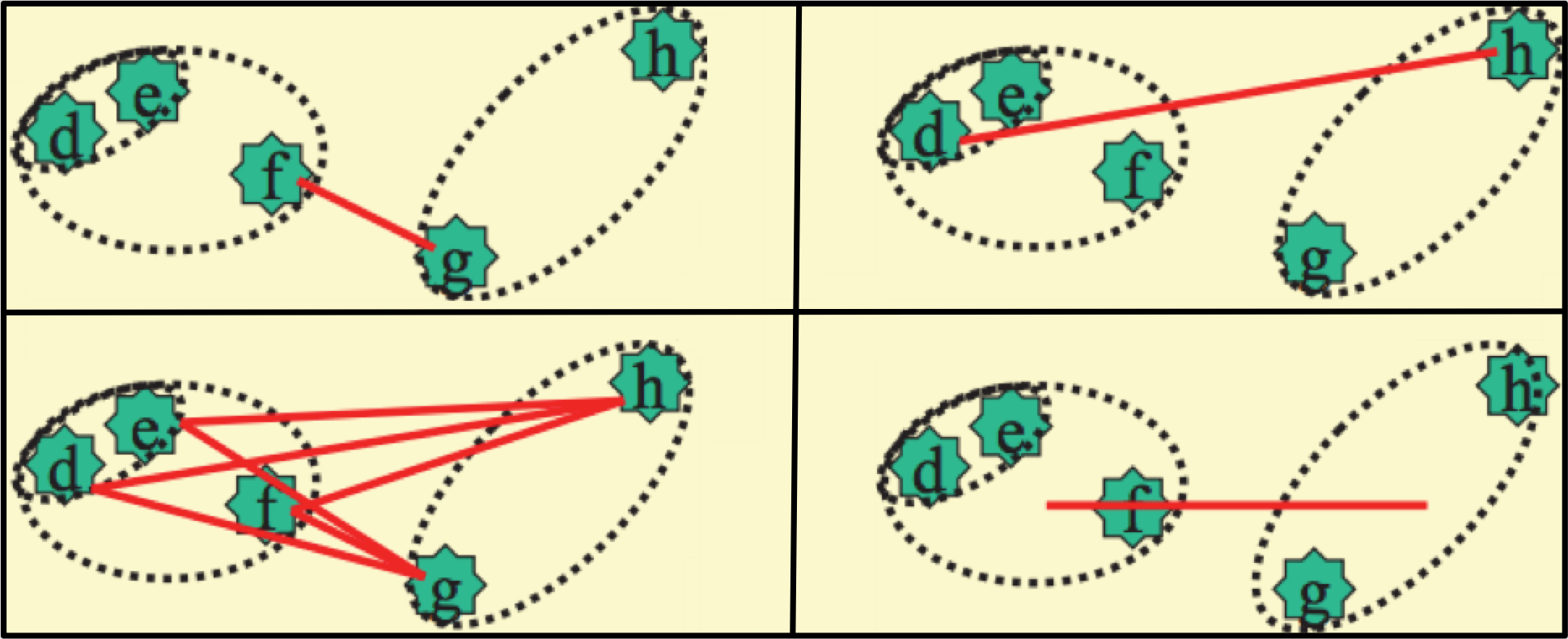
Por supuesto, se requiere un método para determinar distancias entre clústeres. La métrica particular utilizada varía según el contexto, pero (como puede verse en la figura 15.14 algunas implementaciones comunes incluyen la máxima,
las distancias mínimas y medias entre los conglomerados constituyentes, y la distancia entre los centroides de los clústeres.
Señaló que a la hora de elegir los clusters más cercanos, calcular todas las distancias por pares consume mucho tiempo y espacio, por lo que se necesita un mejor esquema. Una forma posible de hacer esto es: 1) definir algunos cuadros delimitadores que dividen el espacio de entidades en varios subespacios 2) calcular distancias por pares dentro de cada cuadro 3) desplazar el límite de las cajas en diferentes direcciones y recalcular distancias por pares 4) elegir el par más cercano en función de los resultados en todas las iteraciones.
Evaluar el desempeño del clúster
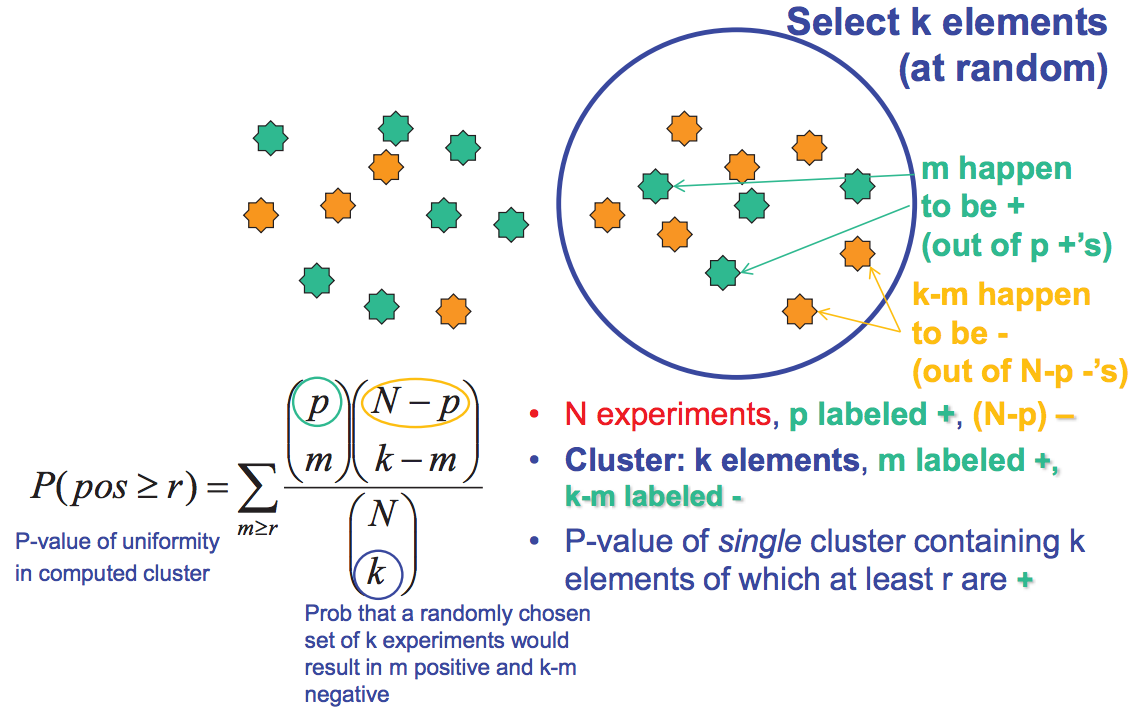
La validez de un agrupamiento particular se puede evaluar de varias maneras diferentes. La sobrerrepresentación de un grupo conocido de genes en un clúster, o, más generalmente, la correlación entre el agrupamiento y las asociaciones biológicas confirmadas, es un buen indicador de validez y significación. Sin embargo, si aún no se dispone de datos biológicos, existen formas de evaluar la validez utilizando estadísticas. Por ejemplo, los clústeres robustos aparecerán a partir de la agrupación incluso cuando solo se utilicen subconjuntos del total de datos disponibles para generar clústeres. Además, la significancia estadística de un agrupamiento se puede determinar calculando la probabilidad de que una distribución particular se haya obtenido aleatoriamente para cada clúster. Este cálculo utiliza variaciones en la distribución hipergeométrica. Como se puede ver en la figura 15.15, podemos hacer esto calculando la probabilidad de que tengamos más de r + cuando seleccionamos k elementos de un total de N elementos. http://en.Wikipedia.org/wiki/Cluster...tering_results da varias fórmulas para evaluar la calidad de la agrupación.