20.5: Métodos estadísticos

¿Qué nos dicen los datos?

Existen dos tipos de datos numéricos adquiridos por los biólogos:

• contar; por ejemplo, el número de hembras en una población
• medir una variable continua como la longitud o el peso

En el primer caso, todos pueden ponerse de acuerdo en el valor “verdadero”. En el segundo caso, los valores medidos siempre reflejan un rango, cuyo tamaño está determinado por factores tales como

• precisión del instrumento de medición y
• variabilidad individual entre los objetos que se están midiendo.

¿Cómo se manejan esos datos?

Cálculo de la desviación estándar

El primer paso es calcular una media (promedio) para todos los miembros del conjunto. Esta es la suma de todas las lecturas divididas por el número de lecturas tomadas.

Pero considere los conjuntos de datos:

46,42,44,45,43 y 52,80,22,30,36

Ambos dan la misma media (44), pero estoy seguro de que se puede ver intuitivamente que un experimentador tendría mucha más confianza en una media derivada del primer conjunto de lecturas que una derivada de la segunda.

Una forma de cuantificar la dispersión de valores en un conjunto de datos es calcular una desviación estándar (S) usando la ecuación

\[s =\sqrt{ \dfrac{\sum (x-\bar{x})^2}{n-1}}\]

donde (“x menos x-bar) ² es el cuadrado de la diferencia entre cada medida individual (x) y la media (“barra x”) de las mediciones. El símbolo sigma indica la suma de estos, y n es el número de mediciones individuales.

Usando el primer conjunto de datos, calculamos una desviación estándar de 1.6.

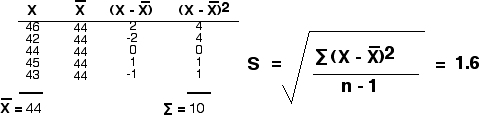
El segundo conjunto de datos produce una desviación estándar de 22.9.

(Muchas calculadoras manuales económicas están programadas para hacer este trabajo por usted cuando simplemente ingresa los valores para X.)

Error estándar de la media

En nuestros dos conjuntos de 5 mediciones, ambos conjuntos de datos dan una media de 44. Pero ambos grupos son muy pequeños. ¿Qué tan seguros podemos estar de que si repetimos las mediciones miles de veces, ambos grupos seguirían dando una media de 44? Para estimar esto, calculamos el error estándar de la media (S.E.M. o S _x-bar) usando la ecuación

\[ S_{\bar{x}} = \dfrac{S}{\sqrt{n}}\]

donde S es la desviación estándar y n es el número de mediciones.

En nuestro primer conjunto de datos, el S.E.M. es 0.7.

\[ S_{\bar{x}} = \dfrac{S}{\sqrt{5}} = \dfrac{1.6}{2.23} = 0.7\]

En el segundo grupo es 10.3.

\[ S_{\bar{x}} = \dfrac{S}{\sqrt{5}} = \dfrac{22.9}{2.23} = 10.3\]

Límites de confianza del 95%

Resulta que existe un 68% de probabilidad de que el valor medio “verdadero” de cualquier efecto que se esté midiendo caiga entre +1 y −1 error estándar (S.E.M.). Dado que esta no es una probabilidad muy fuerte, la mayoría de los trabajadores prefieren extender el rango a límites dentro de los cuales pueden estar 95% seguros de que el valor “verdadero” radica. Este rango es aproximadamente entre −2 y +2 veces el error estándar.

Entonces

• para nuestro primer grupo, 0.7 x 2 = 1.4
• para nuestro segundo grupo, 10.3 x 2 = 20.6

Entonces

• si nuestro primer grupo es representativo de toda la población, estamos 95% seguros de que la media “verdadera” se encuentra entre 42.6 y 45.4 (44 ± 1.4 o 42.6 ≤ 44 ≤ 45.4).
• para nuestro segundo grupo, estamos 95% seguros de que la media “verdadera” se encuentra en algún lugar entre 23.4 y 64.6 (44 ± 20.6 o 23.4 ≤ 44 ≤ 64.6).

Dicho de otra manera, cuando se presenta la media junto con sus límites de confianza del 95%, los trabajadores están diciendo que solo hay una probabilidad de 1 en 20 de que el valor medio “verdadero” se encuentre fuera de esos límites.

Dicho de otra manera: la probabilidad (p) de que el valor medio se encuentre fuera de esos límites es menor que 1 en 20 (p = <0.05).

Un ejemplo:

Supongamos que

• el primer conjunto de datos (” A “) (46,42,44,45,43) representa mediciones de cinco animales a los que se les ha dado un tratamiento particular y
• el segundo conjunto de datos (” B “) (52,80,22,30,36) mediciones de otros cinco animales a los que se les dio un tratamiento diferente.
• Se utilizó un tercer grupo (” C “) de cinco animales como controles; no se les dio ningún tratamiento y sus medidas fueron 20,23,24,19,24. La media del grupo de control es 22, y el error estándar es 2.1.

¿El tratamiento A tuvo un efecto significativo? ¿El tratamiento B?

La gráfica muestra la media de cada conjunto de datos (puntos rojos). Las líneas oscuras representan los límites de confianza del 95% (± 2 errores estándar).

Aunque ambas medias experimentales (A y B) son dos veces más grandes que la media testigo, solo los resultados en A son significativos. El valor “verdadero” de B podría incluso ser simplemente el de los animales no tratados, los controles (C).

Rechazar la hipótesis nula

En principio, un científico diseña un experimento para desmentir, o no, que un efecto observado se debe solo al azar. A esto se le llama rechazar la hipótesis nula.

El valor p es la probabilidad de que no haya diferencia entre el experimental y los controles; es decir, que la hipótesis nula sea correcta. Entonces, si la probabilidad de que la media experimental difiera de la media testigo es mayor a 0.05, entonces la diferencia generalmente no se considera significativa. Si p = <0.05, la diferencia se considera significativa y se rechaza la hipótesis nula.

En nuestro ejemplo hipotético, la diferencia entre el grupo experimental A y los controles (C) parece ser significativa; la diferencia entre B y los controles no.

Reducir los límites de confianza

Se pueden tomar dos enfoques para reducir los límites de confianza.

• ampliar el tamaño de la muestra que se está midiendo (aumenta n)
• encontrar formas de reducir la fluctuación de las mediciones sobre la media.

El segundo objetivo suele ser mucho más difícil de lograr; si resulta imposible, ¡quizás la hipótesis nula sea correcta después de todo!