4.1: Principios Básicos de Catálisis
- Page ID
- 52875
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Una versión imprimible de esta sección está aquí: BiochemFFA_4_1.pdf. Todo el libro de texto está disponible de forma gratuita de los autores en http://biochem.science.oregonstate.edu/content/biochemistry-free-and-easy
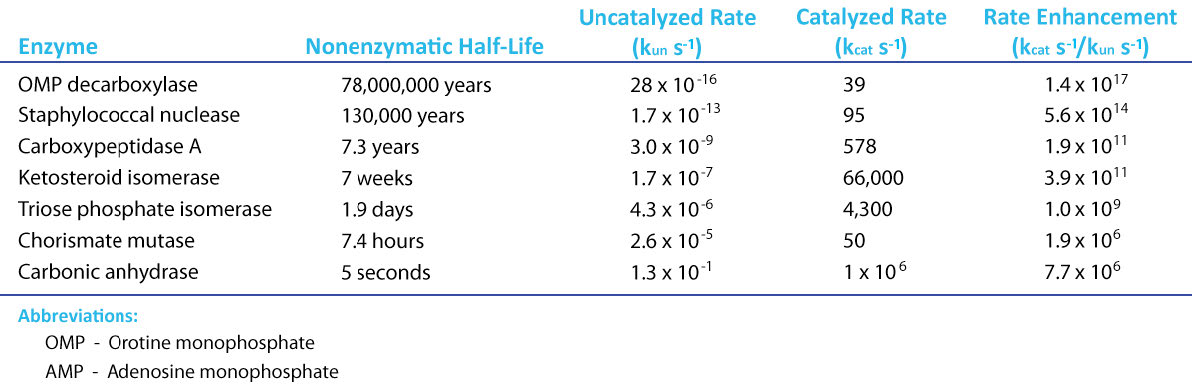
Si hay un componente mágico en la vida, seguramente se puede argumentar para que sea catálisis. Gracias a la catálisis, las reacciones que pueden tardar cientos de años en completarse en el “mundo real” no catalizado, ocurren en segundos en presencia de un catalizador. Los catalizadores químicos, como el platino, pueden acelerar las reacciones, pero las enzimas (que son simplemente súper catalizadores con un “giro”, como veremos) avergüenzan a los catalizadores químicos (Figura 4.1). Para entender la catálisis enzimática, es necesario primero entender la energía. Las reacciones químicas siguen la tendencia universal de avanzar hacia una menor energía, pero a menudo tienen una barrera que debe superarse. El secreto de la acción catalítica es reducir la magnitud de esa barrera.
Antes de discutir las enzimas, es apropiado hacer una pausa y discutir un concepto importante relacionado con las reacciones químicas/bioquímicas. Ese concepto es equilibrio y muy a menudo se malentiende. La parte “equi” de la palabra se refiere a igual, como cabría esperar, pero no se refiere a concentraciones absolutas. Lo que sucede cuando una reacción bioquímica está en equilibrio es que las concentraciones de reactivos y productos no cambian con el tiempo. Esto no quiere decir que las reacciones se hayan detenido. Recuerda que las reacciones son reversibles, por lo que hay una reacción directa y una reacción inversa: si tuviste 8 moléculas de A, y 4 de B al principio, y 2 moléculas de A se convirtieron en B, mientras que 2 moléculas de B se volvieron a convertir simultáneamente en A, el número de moléculas de A y B permanece sin cambios, es decir, la reacción está en equilibrio. No obstante, notará que esto no significa que haya números iguales de moléculas A y B.
Materias de Concentración
Entonces, contrariamente a las percepciones de muchos estudiantes, las concentraciones de productos y reactivos no son iguales en equilibrio, a menos que el ΔG°' para una reacción sea cero, porque cuando este es el caso,
\[ΔG = \ln \left(\dfrac{[\rm{Products}]}{[\rm{Reactants}]} \right)\]
ya que el ΔG°' es cero. Debido a que ΔG en sí es cero en equilibrio, entonces
\[[Products] = [Reactants].\]
Esta es la única circunstancia en la que
\[[Products] = [Reactants]\]
en equilibrio. Reiterando, en equilibrio, las concentraciones de reactivo y producto no cambian con el tiempo. Es decir, para una reacción\(A \rightleftharpoons B [A]\) en el tiempo cero cuando se alcanza el equilibrio\([A]_{T_0}\),, será la misma 5 minutos después (asumiendo que A y B son químicamente estables). Así,
\[[A]_{T_0} = [A]_{T+5}\]
Del mismo modo,
\[[B]_{T_0} = [B]_{T+5}\]
Para el caso, en cualquier cantidad de tiempo X después de que se haya alcanzado el equilibrio,
\[[A]T0 = [A]T+5 = [A]TX\]
y
\[[B]T0 = [B] T+5 = [B]TX\]
Sin embargo, a menos que ΔG°' = 0, es erróneo decir [A] T0 = [B] T0 A medida que estudiamos las reacciones bioquímicas y las velocidades de reacción, es importante recordar que 1) las reacciones generalmente no comienzan en equilibrio; 2) todas las reacciones se mueven en la dirección del equilibrio; y 3) las reacciones en las células se comportan igual que las de prueba tubos - no comienzan en equilibrio, sino que se mueven hacia él. Reacciones dinámicas Las reacciones que ocurren en las células, sin embargo, son muy dinámicas y complejas. En un tubo de ensayo, se pueden estudiar uno a la vez. En las células, el producto de una reacción suele ser el sustrato para otra. Las reacciones en las células están interconectadas de esta manera, dando lugar a lo que se llaman vías metabólicas. De hecho, hay miles de reacciones interconectadas diferentes que ocurren continuamente en las células.
Los intentos de estudiar una sola reacción en el caos de una célula son desalentadores por decir lo menos. Por esta razón, los bioquímicos aíslan enzimas de las células y estudian las reacciones de manera individual. Es con esto en mente que comenzamos nuestra consideración del fenómeno de la catálisis describiendo, primero, la forma en que funcionan las enzimas.
Energía de activación
La Figura 4.2 representa esquemáticamente los cambios de energía que ocurren durante la progresión de una reacción simple. Para que la reacción proceda, se debe superar una energía de activación para que se produzca la reacción.
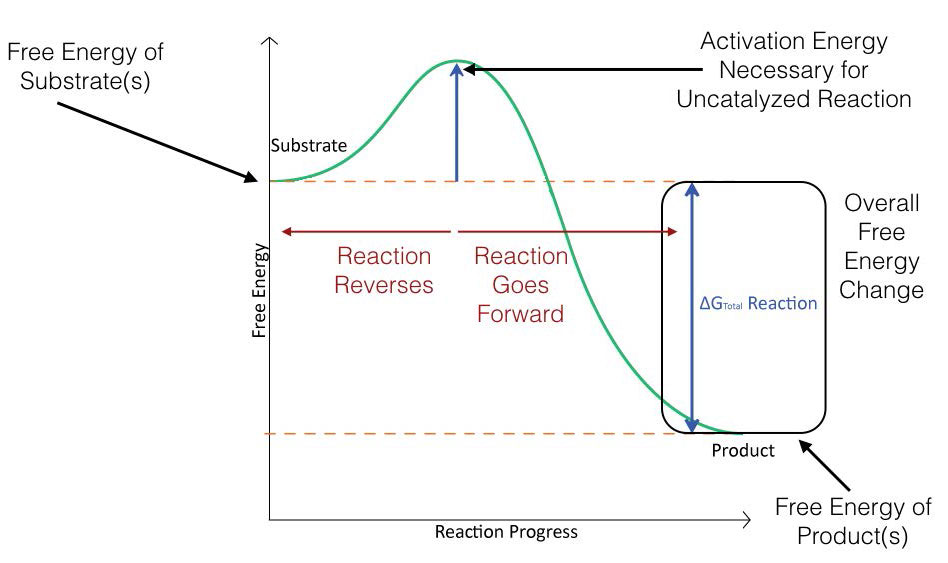
En la Figura 4.3, se superpone la energía de activación para una reacción catalizada. Como puede ver, los reactivos comienzan en el mismo nivel de energía tanto para reacciones catalizadas como no catalizadas y que los productos terminan en la misma energía para ambas también. La reacción catalizada, sin embargo, tiene una menor energía de activación (línea punteada) que la reacción no catalizada. Este es el secreto de la catálisis: el ΔG general para una reacción NO cambia con la catálisis, sino que la energía de activación disminuye.
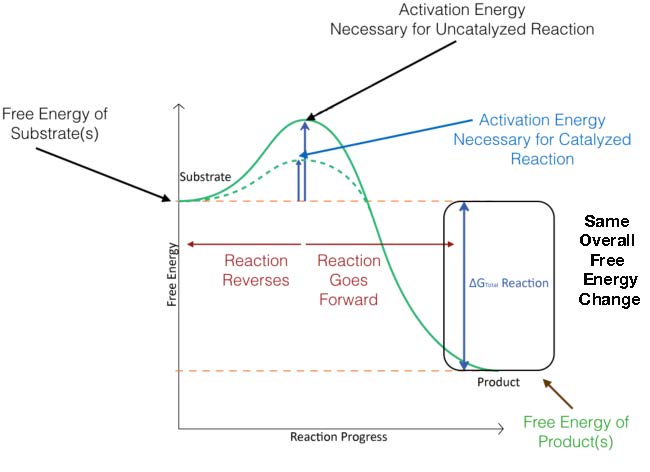
Figura 4.3 - Cambios de energía durante el transcurso de una reacción no catalizada (línea verde continua) y una reacción catalizada (línea verde punteada). Imagen de Aleia Kim
Reversibilidad
La medida en que las reacciones avanzarán es una función del tamaño de la diferencia de energía entre los estados producto y reactivo. Cuanto menor sea la energía de los productos en comparación con los reactivos, mayor será el porcentaje de moléculas que estarán presentes como productos en equilibrio. Vale la pena señalar que dado que una enzima disminuye la energía de activación para una reacción, puede acelerar la inversión de una reacción del mismo modo que acelera una reacción en la dirección hacia adelante. En equilibrio, por supuesto, no se produce ningún cambio en la concentración de reactivos y productos. Así, las enzimas aceleran el tiempo requerido para alcanzar el equilibrio, pero no afectan el equilibrio de productos y reactivos en equilibrio.
Excepciones
La reversibilidad de las reacciones enzimáticas es una consideración importante para el equilibrio, la medición de la cinética enzimática, para la energía libre de Gibbs, para las vías metabólicas y para la fisiología. Sin embargo, hay algunas excepciones menores a la reversibilidad de las reacciones. Están relacionados con la desaparición de un sustrato o producto de una reacción. Considere la primera reacción a continuación que es catalizada por la enzima anhidrasa carbónica:
\[CO_2 + H_2O \rightleftharpoons H_2CO_3 \rightleftharpoons HCO_3^- + H^+\]
En la dirección hacia adelante, el ácido carbónico se produce a partir del agua y el dióxido de carbono. Puede permanecer intacto en la solución o ionizarse para producir ion bicarbonato y un protón. En sentido inverso, se producen agua y dióxido de carbono. El dióxido de carbono, por supuesto, es un gas y puede dejar la solución y escapar.
Cuando se eliminan las moléculas de reacción, como serían si el dióxido de carbono escapara, la reacción se tira en la dirección de la molécula que se pierde y no puede ocurrir la inversión a menos que se reemplace la molécula faltante. En la segunda reacción que se produce a la derecha, el ácido carbónico (H2CO3) se “elimina” por ionización. Esto también limitaría la reacción volviendo al dióxido de carbono en el agua. Este último tipo de “eliminación” es lo que ocurre en las vías metabólicas. En este caso, el producto de una reacción (ácido carbónico) es el sustrato para la siguiente (formación de bicarbonato y un protón).
En la vía metabólica de la glucólisis, diez reacciones están conectadas de esta manera y revertir el proceso es mucho más complicado que si solo se estuviera considerando una reacción.
Mecanismos generales de acción
Como se señaló anteriormente, las reacciones catalizadas enzimáticamente son órdenes de magnitud más rápidas que las reacciones no catalizadas y catalizadas químicamente. El secreto de su éxito radica en una diferencia fundamental en sus mecanismos de acción.
A cada estudiante de química se le ha enseñado que un catalizador acelera una reacción sin ser consumido por él. En otras palabras, el catalizador termina después de una reacción justo de la manera en que comenzó para que pueda catalizar otras reacciones, también. Las enzimas comparten esta propiedad, pero en el medio, durante la acción catalítica, una enzima se cambia transitoriamente. De hecho, es la capacidad de cambio de una enzima lo que lleva a su increíble eficiencia como catalizador.
Cambios
Estos cambios pueden ser sutiles electrónicos, modificaciones covalentes más significativas o cambios estructurales derivados de la flexibilidad inherente a las enzimas, pero no presentes en los catalizadores químicos. La flexibilidad permite el movimiento y el movimiento facilita la alteración de los entornos electrónicos necesarios para la catálisis. Las enzimas son, por lo tanto, mucho más eficientes que los catalizadores químicos rígidos como resultado de sus capacidades para facilitar los cambios necesarios para optimizar el proceso catalítico.
Encuadernación sustrato
Otra diferencia importante entre el mecanismo de acción de una enzima y un catalizador químico es que una enzima tiene sitios de unión que no solo 'agarran' el sustrato (molécula involucrada en la reacción que se cataliza), sino que también lo colocan en una posición para ser inducido electrónicamente a reaccionar, ya sea dentro de sí mismo o con otro sustrato.
La enzima misma puede desempeñar un papel en la inducción electrónica o la inducción puede ocurrir como resultado de que los sustratos se colocan muy cerca unos de otros. Los catalizadores químicos no tienen tal capacidad para unir sustratos y dependen de que colisionen en la orientación correcta en o cerca de sus superficies.
Sitio activo
Las reacciones en una enzima se catalizan en una ubicación específica dentro de ella conocida como el 'sitio activo'. Los sustratos se unen en el sitio activo y están orientados para proporcionar acceso para la porción relevante de la molécula al entorno electrónico de la enzima donde ocurre la catálisis.
Flexibilidad enzimática
Como se mencionó anteriormente, una diferencia entre una enzima y un catalizador químico es que una enzima es flexible. Sus ligeros cambios de forma (a menudo derivados de la unión del propio sustrato) ayudan a posicionar de manera óptima los sustratos para la reacción después de que se unan.
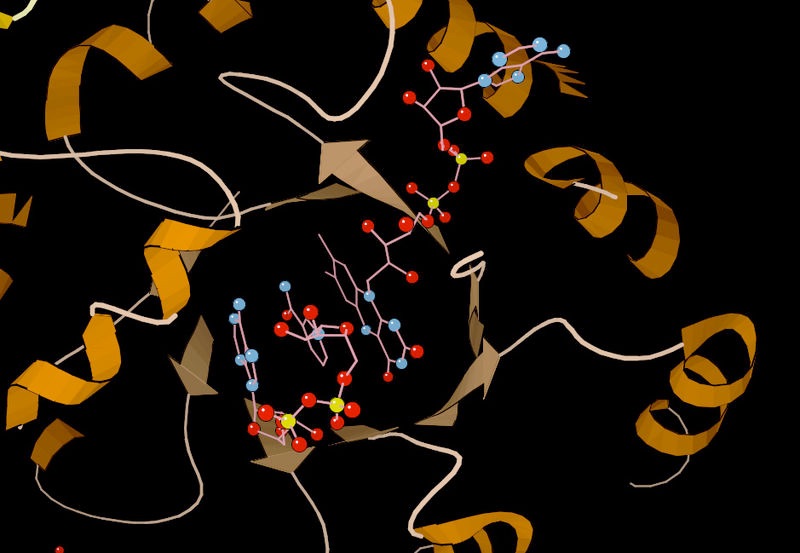
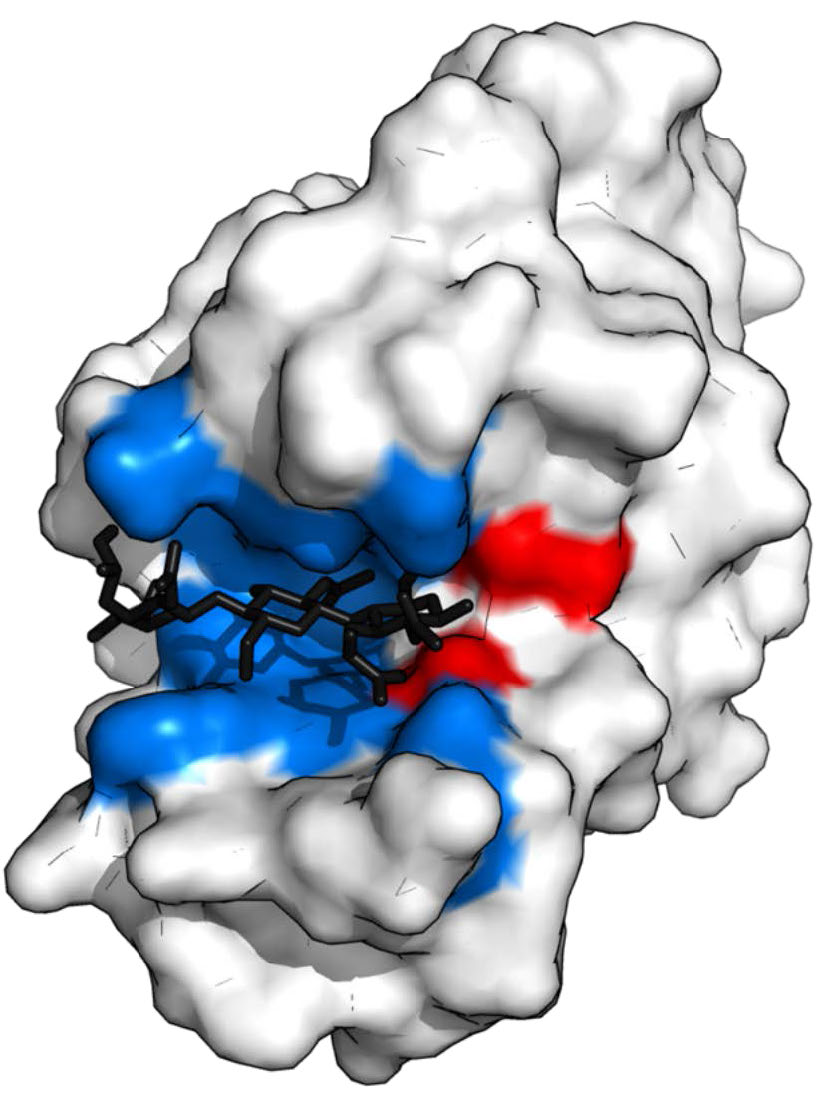
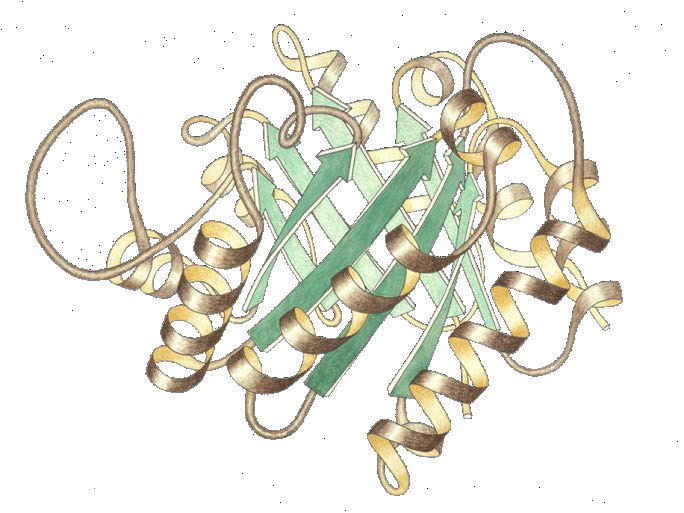
Figura 4.5 - Lisozima con sitio de unión al sustrato (azul), sitio activo (rojo) y sustrato unido (negro). Wikipedia
Ajuste inducido
Estos cambios de forma se explican, en parte, por el Modelo de Catálisis de Ajuste Inducido de Koshland (Figura 4.6), que ilustra que no solo las enzimas cambian los sustratos, sino que los sustratos también cambian transitoriamente la estructura enzimática. Al final de la catálisis, la enzima vuelve a su estado original. El modelo de Koshland contrasta con el modelo Fischer Lock and Key, que dice simplemente que una enzima tiene una forma fija que se adapta perfectamente para unir su (s) sustrato (s). La flexibilidad enzimática también es importante para el control de la actividad enzimática. Las enzimas alternan entre el estado T (apretado), que es un estado de menor actividad y el estado R (relajado), que tiene mayor actividad.
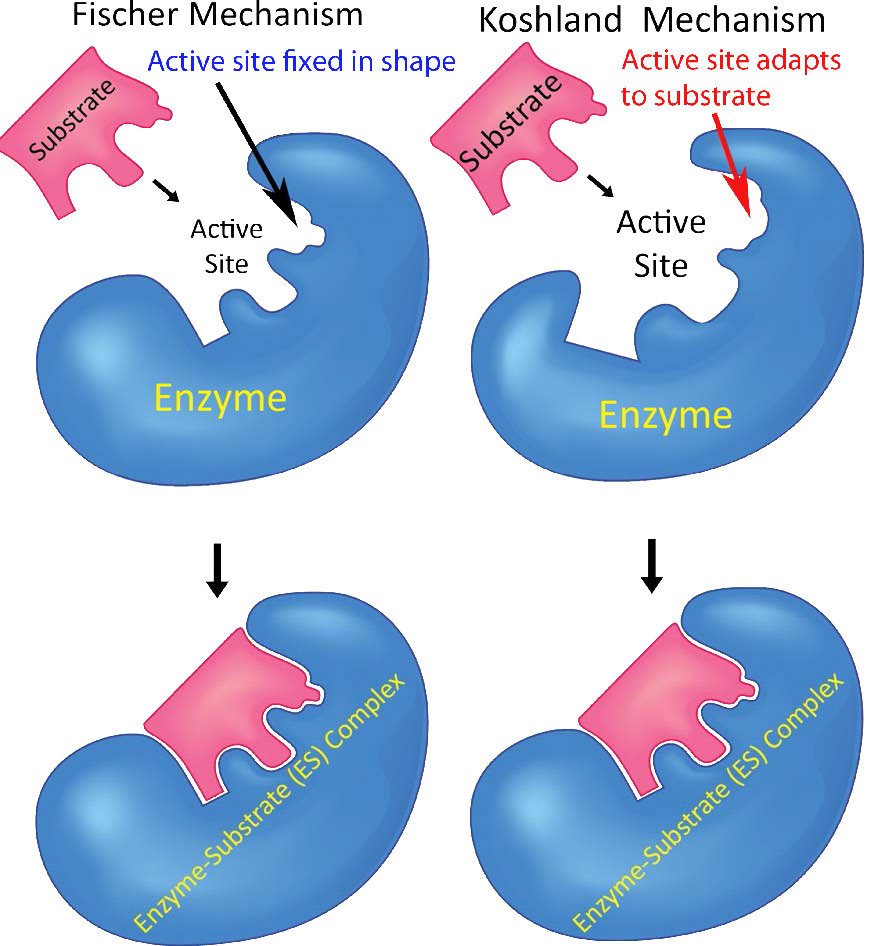
Ajuste inducido
El modelo de catálisis de Koshland Induced Fit postula que las enzimas son flexibles y cambian de forma sobre el sustrato de unión. Los cambios en la forma ayudan a 1) ayudar a la unión de sustratos adicionales en reacciones que involucran más de un sustrato y/o 2) facilitan la formación de un ambiente electrónico en la enzima que favorece la catálisis. Este modelo contrasta con el modelo de catálisis Fischer Lock and Key que considera que las enzimas tienen sitios de unión al sustrato preformados.
Encuadernación ordenada
El modelo de Koshland es consistente con enzimas de unión multisustrato que exhiben unión ordenada de sustratos. Para estos sistemas, la unión del primer sustrato induce cambios estructurales en la enzima necesarios para unirse al segundo sustrato.
Existe considerable evidencia experimental que respalda el modelo Koshland. La hexoquinasa, por ejemplo, es una de las muchas enzimas conocidas por sufrir una alteración estructural significativa después de la unión del sustrato. En este caso, los dos sustratos se acercan muy cerca por el ajuste inducido y como resultado se hace posible la catálisis.
Tipos de reacción
Enzimas que catalizan reacciones que involucran más de un sustrato, como
\[A + B \rightleftharpoons C + D\]
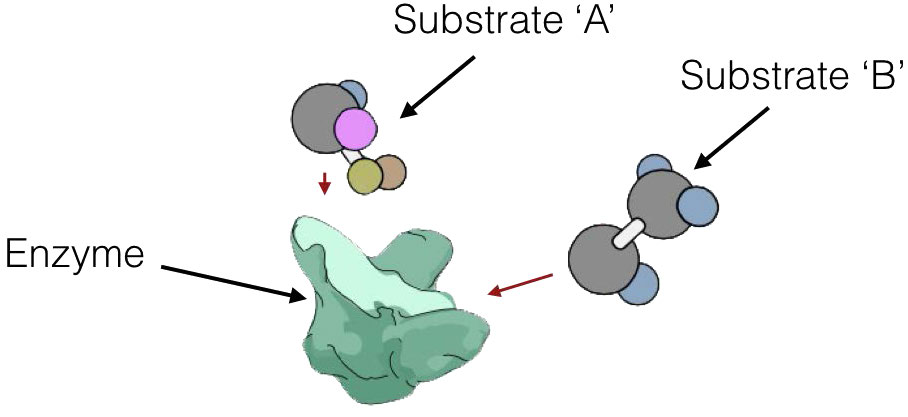
puede actuar de dos maneras distintas. Las reacciones enzimáticas pueden ser de varios tipos, como se muestra en la Figura 4.7. En un mecanismo, denominado reacciones secuenciales, en algún momento de la reacción, ambos sustratos se unirán a la enzima. Hay, a su vez, dos formas diferentes en las que esto puede ocurrir: aleatorio y ordenado.
| Tipos de reacciones | |
|---|---|
| Sustrato Único - Producto Único | A B |
| Sustrato Único - Múltiples Productos | A B + C |
| Múltiples Sustratos - Productos Individuales | A + B C |
| Múltiples Sustratos - Múltiples Productos | A + B C + D |
Considere la lactato deshidrogenasa, que cataliza la siguiente reacción:
\[NADH + Pyruvate → Lactate + NAD^+\]
Esta enzima requiere que el NADH debe unirse antes de la unión del piruvato. Como se señaló anteriormente, esto es consistente con un modelo de catálisis de ajuste inducido. En este caso, la unión del NADH cambia la forma/ambiente de la enzima para que el piruvato pueda unirse y sin unión de NADH, el sustrato no puede acceder al sitio de unión al piruvato. Este tipo de reacción de sustrato múltiple se denomina unión ordenada secuencial, debido a que la unión de los sustratos debe ocurrir en el orden correcto para que la reacción continúe.
Encuadernación aleatoria
Un segundo mecanismo de unión/catálisis es exhibido por la creatina quinasa que cataliza la siguiente reacción:
\[Creatine + ATP → \text{Creatine phosphate} + ADP\]
Para esta enzima, los sustratos pueden unirse a ella en cualquier orden. La creatina quinasa muestra una unión aleatoria secuencial. Cabe mencionar que la unión aleatoria no es inconsistente con el modelo de ajuste inducido de Koshland. Más bien, la unión aleatoria simplemente significa que el ajuste inducido por la enzima no afecta a los sitios de unión al sustrato e involucra otras partes de la enzima. En resumen, la unión secuencial puede ocurrir como unión ordenada o como unión aleatoria.
Reacciones de doble desplazamiento
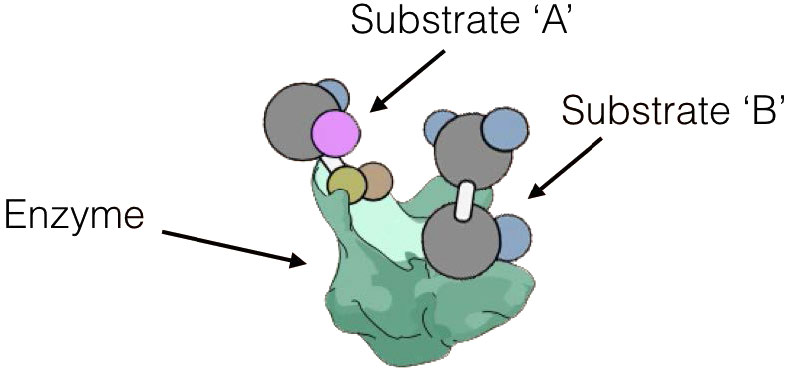
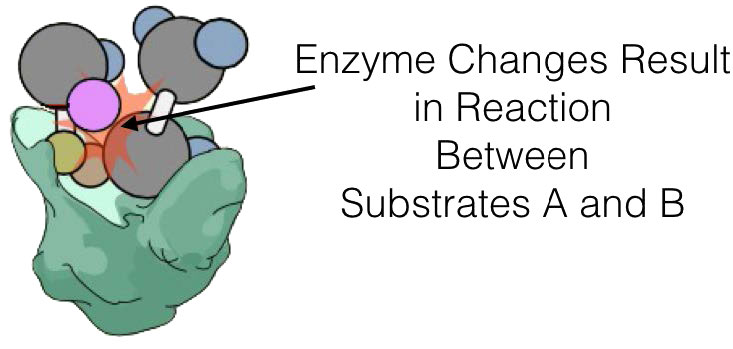
No todas las enzimas que catalizan reacciones multisustrato, sin embargo, se unen a A y B por los mecanismos secuenciales anteriores. Esta otra categoría de enzimas incluye aquellas que exhiben lo que se denominan mecanismos de “ping-pong” (o doble desplazamiento). En estas enzimas, la enzima funciona como catalizador y portador de un grupo entre sustratos unidos individualmente. Ejemplos de este tipo de enzimas incluyen la clase de enzimas conocidas como transaminasas. Una forma general de las reacciones catalizadas por estas enzimas se muestra en la Figura 4.8.
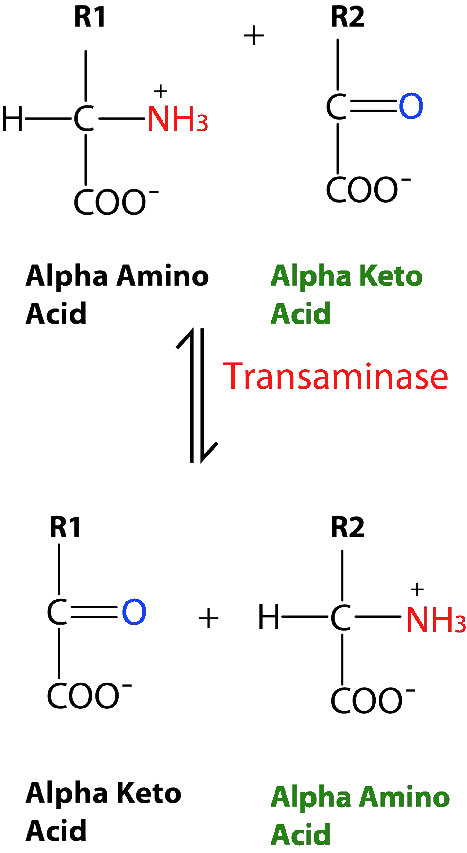
En las reacciones transaminasas reversibles, un oxígeno y una amina están intercambiando entre las moléculas. Se puede representar de la siguiente manera (donde N es la amina y O es el oxígeno).
A=O + C=N B-N + D=O
Esta reacción no ocurre como una reacción de transferencia intercambiando el N y el O, sino como un conjunto de dos medias reacciones. En este caso, la enzima es tanto donante como portadora del grupo que se intercambia. La primera media reacción va de la siguiente manera
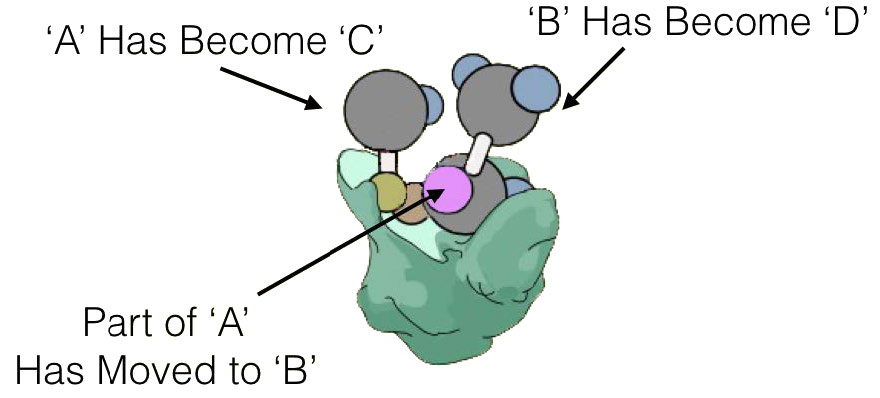
A=O + Enz-N B-N + Enz=O
Siguiente una segunda media reacción va como
C-N + Enz=O D=O + Enz=N
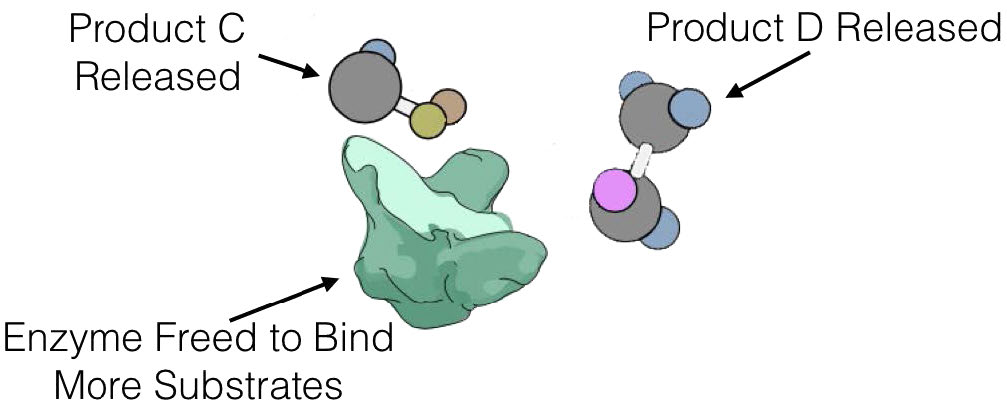
La suma de estas medias reacciones es entonces
A=O + C=N B-N + D=O
Obsérvese que en ningún momento la enzima se unió tanto a A como a C simultáneamente. También es importante reconocer que la enzima existió en dos estados: Enz=O y Enz-N. El barajado de la enzima entre estos dos estados es lo que da lugar al nombre de ping-pong de este mecanismo -literalmente va de un lado a otro como una pelota de ping-pong en un partido de tenis de mesa.
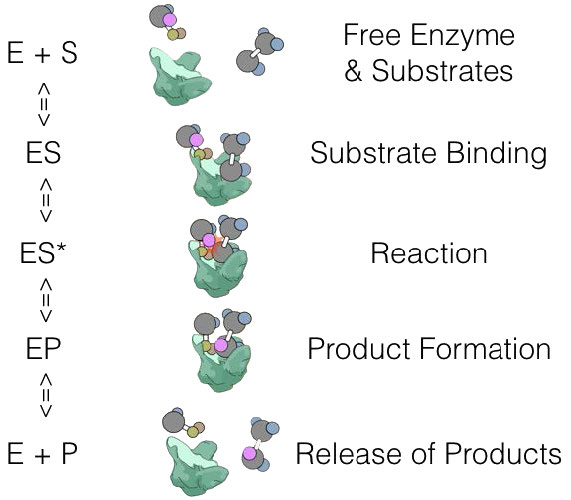
Cinética enzimática
Para entender cómo una enzima potencia la velocidad de una reacción, debemos entender la cinética enzimática. Presentamos aquí un modelo propuesto por Leonor Michaelis y Maud Menten. Para entender el modelo, es necesario comprender algunos parámetros.
Primero, describimos una reacción en términos simples procediendo de la siguiente manera
E + S ES -> E + P
donde E es enzima, S es sustrato y P es producto. En este esquema, ES es el complejo Enzima-Sustrato, que es simplemente la enzima unida a su sustrato.
Podríamos definir un poco más el estado ES con
E + S ES -> ES* -> EP -> E + P
donde ES* es el estado activado y EP es el complejo enzima-producto antes de la liberación del producto.
La primera consideración que tenemos es la velocidad. La velocidad de una reacción es la velocidad de creación del producto a lo largo del tiempo, medida como la concentración de producto por tiempo. El tiempo es una consideración crítica a la hora de medir la velocidad. En un sistema cerrado (en el que opera una enzima), todas las reacciones avanzarán hacia el equilibrio. Las reacciones catalizadas enzimáticamente no son diferentes en el resultado final de las reacciones no enzimáticas, excepto que llegan al equilibrio más rápido.
Equilibrio
En equilibrio, la relación de producto a reactivo no cambia. Esa es una propiedad del equilibrio. Dado que el sistema está cerrado, la concentración del producto a lo largo del tiempo no cambiará. La velocidad será así cero bajo estas condiciones y no habremos aprendido nada de la reacción si esperamos demasiado para estudiarla.
Velocity
En consecuencia, en la cinética de Michaelis-Menten, la velocidad se mide como velocidad inicial (V0). Esto se logra midiendo la velocidad de formación del producto temprano en la reacción antes de que se establezca el equilibrio y bajo estas condiciones, hay muy poca, si alguna, de la reacción inversa que ocurre.
Los otros dos supuestos están relacionados. Primero, utilizamos condiciones donde hay mucho más sustrato que enzima. Esto tiene sentido. Si el sustrato no está en gran exceso, entonces la conversión de sustrato en producto por parte de la enzima ocurrirá mucho más rápido de lo que la enzima puede unirse al sustrato.
Esperando sustrato
Así, la enzima “esperaría” a que el sustrato se uniera si no hubiera cantidades suficientes de éste para unirse a la enzima de manera oportuna (cuando la concentración de sustrato es baja). Esto no daría una medida precisa de la velocidad, ya que la enzima estaría inactiva buena parte del tiempo. Debido a esto, asumimos que la saturación de la enzima con sustrato dará una velocidad máxima de reacción.
Estado estacionario
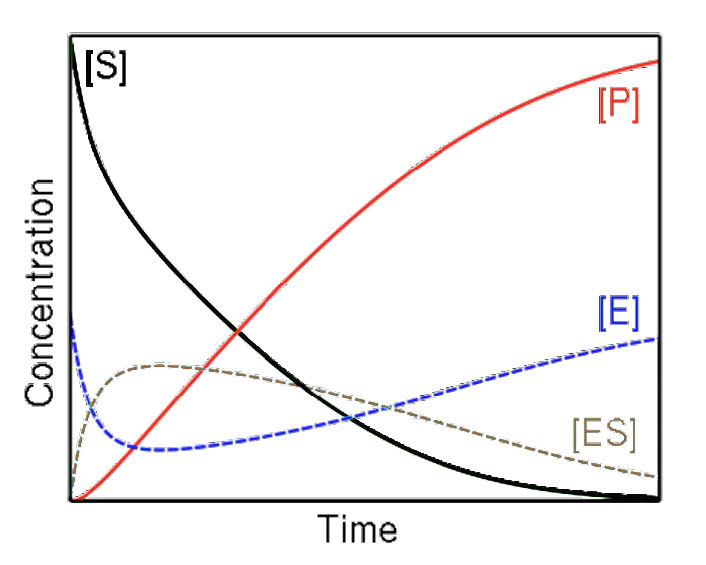
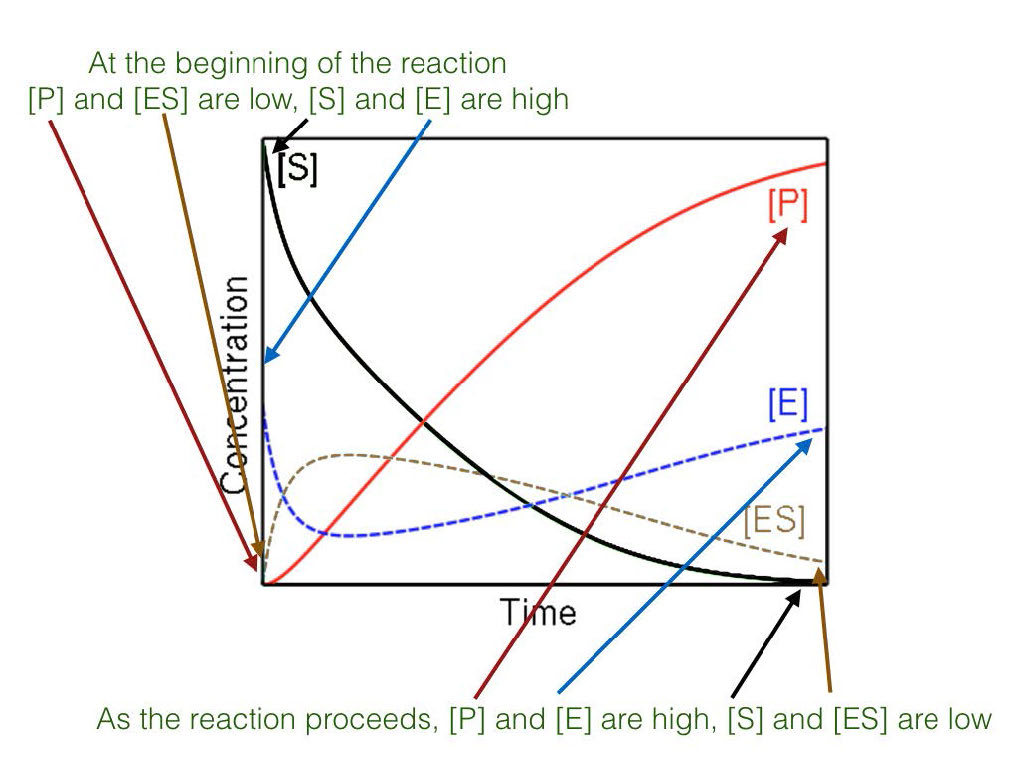
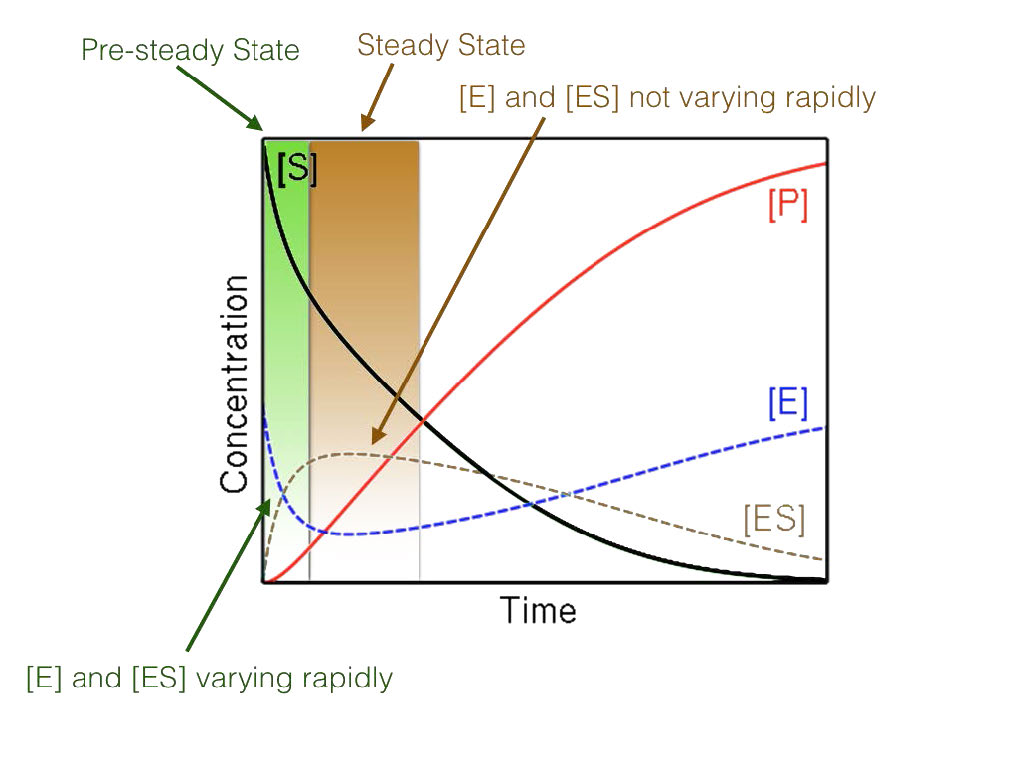
Figura 4.17 - Estado estacionario versus estado no estacionario
Por último, la alta concentración de sustrato combinada con la medición de las condiciones iniciales da como resultado el estudio de reacciones que se encuentran bajo las llamadas condiciones de estado estacionario (Figura 4.17). Cuando ocurre el estado estacionario, la concentración del complejo ES a lo largo del tiempo no cambia significativamente durante el periodo de análisis.
Reiterando, los tres supuestos para la cinética de Michaelis-Menten son
- Medición de la velocidad inicial de una reacción
- Sustrato en gran exceso comparado con la enzima
- Condiciones de reacción que ocurren en estado estacionario
Consideraciones experimentales
Ahora volvemos nuestra atención a cómo se realizan los estudios de las propiedades cinéticas de una enzima. Para realizar un análisis, se haría el siguiente experimento: se configurarían 20 tubos diferentes con tampón enzimático (para mantener estable la enzima), la misma cantidad de enzima, y luego una cantidad diferente de sustrato en cada tubo, que van desde pequeñas cantidades en los primeros tubos hasta cantidades muy grandes en los últimos tubos. La reacción se dejaría continuar durante un tiempo fijo, corto y luego la reacción se detendría y se determinaría la cantidad de producto contenido en cada tubo.
La velocidad inicial (V0) de la reacción sería entonces la concentración de producto que se encuentra en cada tubo dividida por el tiempo en que se dejó correr la reacción. Los datos del experimento se representarían en una gráfica utilizando la velocidad inicial (V0) en el eje Y y la concentración de sustrato en el eje X, teniendo cada tubo, por supuesto, una velocidad de reacción única correspondiente a una concentración de sustrato única.
Para una enzima siguiendo la cinética de Michaelis-Menten resultaría una curva como la mostrada en la Figura 4.18 o 4.19. A baja concentración de sustrato, es limitante y la enzima lo convierte en producto tan pronto como puede enlazarlo. En consecuencia, a bajas concentraciones de sustrato, la tasa de incremento de [P] es casi lineal con [S] (Figura 4.19).
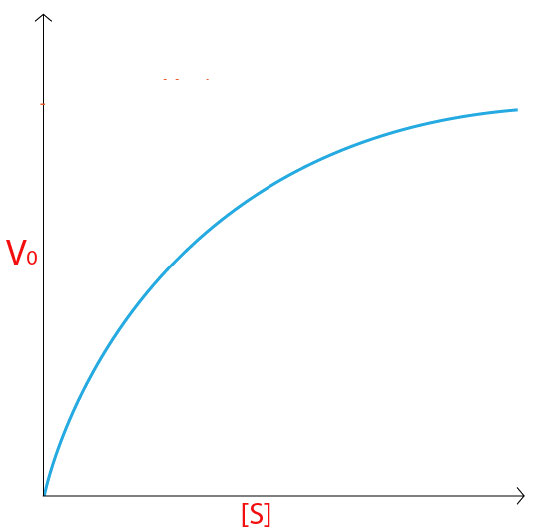
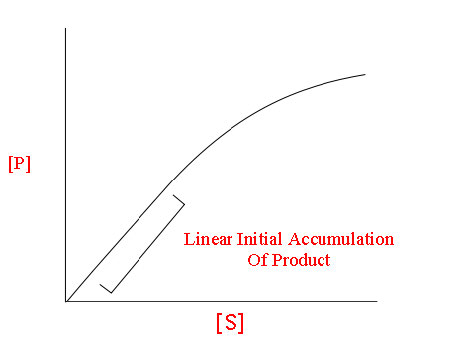
Figura 4.19 - Relación lineal entre [P] y [S] a baja [S]
Incremento no lineal
A medida que aumenta la concentración de sustrato, sin embargo, la velocidad de la reacción en tubos con mayor concentración de sustrato deja de aumentar linealmente y en su lugar comienza a aplanarse, lo que indica que a medida que la concentración de sustrato aumenta cada vez más, la enzima tiene más dificultad para mantenerse al día para convertir el sustrato a producto.
Saturación
No en vano, cuando la enzima se satura completamente con sustrato, no tendrá que esperar a que el sustrato se difunda hacia él y por lo tanto estará operando a máxima velocidad.
Para una enzima que sigue la cinética de Michaelis-Menten tendrá su velocidad (v) a cualquier concentración de sustrato dada por la siguiente ecuación:
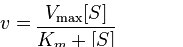
V máx
Dos términos de la ecuación anterior requieren explicación. El primero es V max. Se refiere a la velocidad máxima de una reacción enzimática. La velocidad máxima para una reacción ocurre cuando una enzima se satura con sustrato. La saturación es importante porque significa (según el supuesto anterior) que ninguna de las moléculas enzimáticas está “esperando” el sustrato después de que se libere un producto. La saturación asegura que otro sustrato esté siempre disponible instantáneamente. La unidad de V max es concentración de producto por tiempo = [P] /tiempo.
En una gráfica de velocidad inicial versus concentración de sustrato (V0 vs. [S]), V max es el valor en el eje Y al que se aproxima asintóticamente la curva (línea punteada en la Figura 4.20). Cabe señalar que el valor de V max depende de la cantidad de enzima utilizada en una reacción. Si duplica la cantidad de enzima utilizada, duplicará la V máx. Si se quisieran comparar las velocidades de dos enzimas diferentes, sería necesario utilizar las mismas cantidades de enzima en la reacción que cataliza cada una.
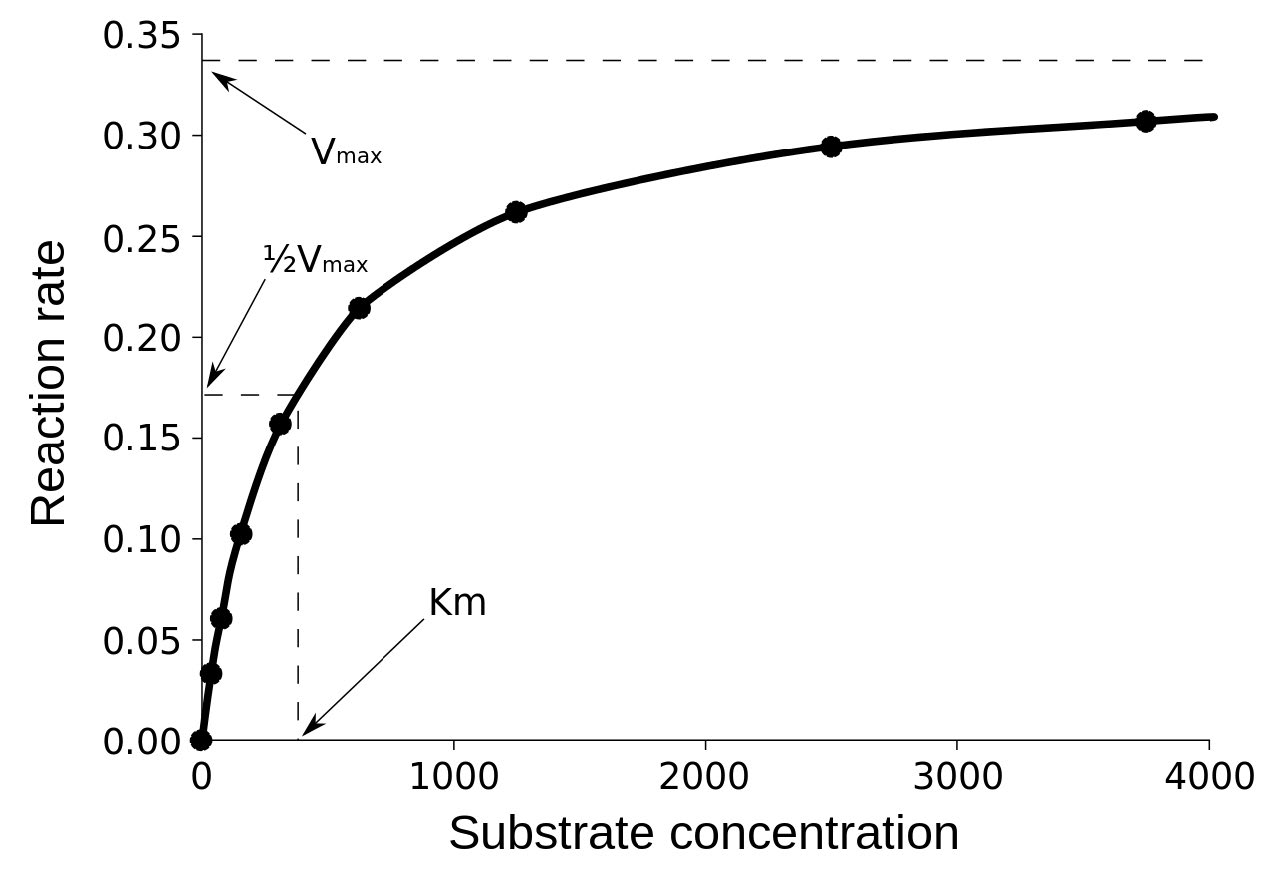
Km
El segundo término es Km (también conocido como Ks). Denominada como la constante de Michaelis, Km es la concentración de sustrato que hace que la enzima trabaje a la mitad de la velocidad máxima (Vmax/2). Lo que mide, en términos simples, es la afinidad que tiene una enzima por su sustrato. El valor de Km está inversamente relacionado con la afinidad de la enzima por su sustrato. Las enzimas con un alto valor de Km tendrán una menor afinidad por su sustrato (tomarán más sustrato para llegar a Vmax/2) mientras que aquellas con un Km bajo tendrán alta afinidad y tomarán menos sustrato para llegar a Vmax/2. La unidad de Km es la concentración.
Las afinidades de las enzimas por los sustratos varían considerablemente, por lo que conocer Km nos ayuda a comprender qué tan bien se adapta una enzima al sustrato que se está utilizando. La medición de Km depende de la medición de Vmax.
Error común
Un error común que cometen los estudiantes al describir Vmax es decir que Km = Vmax /2. Esto, por supuesto, no es cierto. Km es una concentración de sustrato y es la cantidad de sustrato que necesita para que una enzima alcance Vmax /2. Por otro lado Vmax /2 es una velocidad y una velocidad ciertamente no puede igualar una concentración.
Kcat
Es deseable tener una medida de velocidad que sea independiente de la concentración de la enzima. Recuerda que Vmax dependía de la cantidad de enzima utilizada. Para ello, utilizamos el Kcat, también conocido como el número de facturación. Kcat es un número que requiere uno para determinar primero Vmax para una enzima y luego dividir el Vmax por la concentración de enzima utilizada para determinar Vmax. Así,
Kcat = Vmax/[Enzima]
Dado que Vmax tiene unidades de concentración por tiempo y [Enzima] tiene unidades de concentración, las unidades en Kcat son tiempo-1. Si bien eso puede parecer poco intuitivo, significa que el valor de Kcat es el número de moléculas de producto elaboradas por cada molécula de enzima en el tiempo dado. Entonces, un valor de Kcat de 1000/seg significa que cada molécula de enzima en la reacción a Vmax está produciendo 1000 moléculas de producto por segundo. Tenga en cuenta que dado que Kcat es un valor calculado, no se puede leer de una gráfica V vs [S] como Vmax y Km pueden.

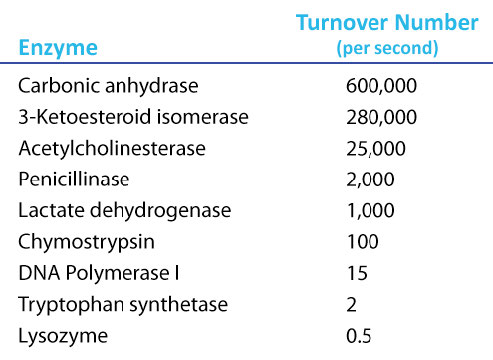
Increíbles valores de Kcat
Un valor de Kcat de 1000 moléculas de producto por enzima por segundo puede parecer un valor alto, pero existen enzimas conocidas (anhidrasa carbónica, por ejemplo) que tienen un valor de Kcat superior a 600.000/segundo (Figura 4.21). Este asombroso valor ilustra claramente por qué las enzimas parecen casi mágicas en su acción. En contraste con\(V_{max}\), que varía con la cantidad de enzima utilizada, Kcat es una constante para una enzima bajo condiciones dadas.
Como se vio anteriormente, las enzimas que siguen la cinética de Michaelis-Menten producen gráficas hiperbólicas de Velocidad (V0) versus Concentración de Sustrato [S] (Figura 4.18). Sin embargo, no todas las enzimas siguen la cinética de Michaelis-Menten. Muchas enzimas tienen múltiples subunidades proteicas y estas a veces interactúan de manera diferente tras la unión de un sustrato o una molécula externa. Consulte ATCase (AQUÍ) para ver un ejemplo.
Enzimas perfectas
Ahora bien, si pensamos en lo que podría ser una enzima ideal, sería aquella que tenga una velocidad muy alta y una afinidad muy alta por su sustrato. Es decir, no se necesitaría mucho sustrato para llegar a Vmax/2 y el Kcat sería muy alto. Dichas enzimas tendrían valores de Kcat/Km que son máximos. Curiosamente, hay varias enzimas que tienen esta propiedad y sus valores máximos de Kcat/Km son todos aproximadamente los mismos. Dichas enzimas son referidas como “perfectas” porque han alcanzado el máximo valor posible.
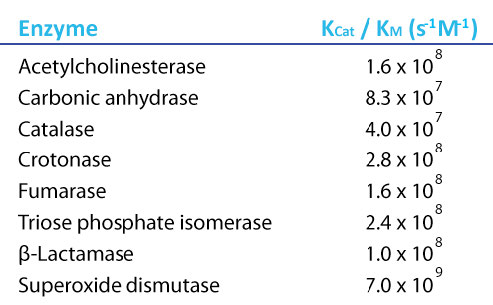
Figura 4.22 - Valores de Kcat/Km para enzimas perfectas. Imagen de Aleia Kim


Limitación de difusión
¿Por qué debería haber un valor máximo posible de Kcat/Km? La respuesta es que el movimiento del sustrato hacia la enzima se convierte en el factor limitante para las enzimas perfectas. El movimiento del sustrato por difusión en agua tiene una velocidad fija a cualquier temperatura y esa limitación finalmente determina la velocidad máxima a la que una enzima puede catalizar. En una analogía macroscópica mundial, las fábricas no pueden fabricar productos más rápido de lo que los proveedores pueden entregar materiales. Es seguro decir para una enzima perfecta que el único límite de velocidad que tiene es la velocidad de difusión del sustrato en el agua.
Dada la “magia” de las enzimas aludidas anteriormente, podría parecer que todas las enzimas debieron haber evolucionado para ser “perfectas”. Hay muy buenas razones por las que la mayoría de ellos no lo han hecho.
Velocidad
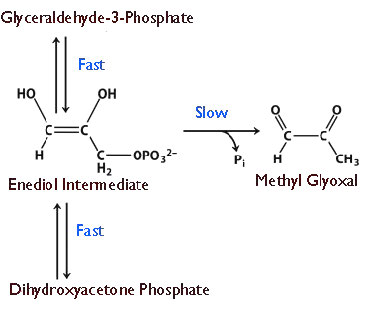
La velocidad es algo peligroso. Cuanto más rápido transcurre una reacción en la catálisis por una enzima, más difícil es controlarla. Como todos sabemos por aprender a conducir, el exceso de velocidad provoca accidentes. Así como los conductores necesitan tener límites de velocidad para operar automóviles, también las células deben ejercer cierto control sobre el 'acelerador' de sus enzimas. En vista de esto, uno podría preguntarse entonces por qué alguna célula ha evolucionado alguna enzima a la perfección. No hay una respuesta única a la pregunta, pero una común es ilustrada por la triosa fosfato isomerasa, la cual cataliza una reacción en la glucólisis que se muestra en la Figura 4.24.
La enzima parece haber evolucionado esta capacidad debido a que a velocidades más bajas, hay descomposición de un intermedio de enediol inestable que luego forma fácilmente metilglioxal, un compuesto citotóxico (Figura 4.25). La aceleración de la reacción proporciona menos oportunidades para que el intermedio inestable se acumule y se hagan menos subproductos indeseables.
Constante de disociación
Al estudiar proteínas y ligandos, es importante entender la “estanqueidad” con la que una proteína (P) “se sujeta” a un ligando (L). Esto se mide con la constante de disociación (\(K_d\)). La formación de un complejo ligando-proteína\(LP\) ocurre como
\[L + P \rightleftharpoons LP\]
La disociación del complejo, por lo tanto, es la inversa de esta reacción, o
\[LP \rightleftharpoons L + P\]
por lo que la constante de disociación correspondiente se define como
\[K_d = \dfrac{[L][P]}{[LP]}\]
donde\([L]\),\([P]\), y\([LP]\) son las concentraciones molares de la proteína, el ligando y el complejo cuando se unen entre sí.
Los valores más pequeños\(K_d\) indican una unión estrecha, mientras que los valores más grandes indican una unión suelta. La constante de disociación es la inversa de la constante de asociación.
\[K_a = \dfrac{1}{K_d}\]
Donde múltiples moléculas se unen entre sí, como
\[J_xK_y \rightleftharpoons xJ + yK\]
El complejo\(J_xK_y\) se descompone en\(x\) subunidades de\(J\) y\(y\) subunidades de\(K\). La constante de disociación se define entonces como
\[K_d = \dfrac{[J]^x[K]^y}{[J_xK_y]}\]
donde\([J]\)\([K]\), y\([J_xK_y]\) son las concentraciones de J, K y el complejo\(J_xK_y\), respectivamente.
Parcelas Lineweaver-Burk
El estudio de la cinética enzimática es típicamente el componente más intensivo en matemáticas de la bioquímica y uno de los aspectos más desalentadores de la asignatura para muchos estudiantes. Si bien se intenta simplificar las consideraciones matemáticas, a veces solo sirven para confundir o frustrar a los estudiantes. Tal es el caso de las gráficas enzimáticas modificadas, como Lineweaver-Burk (Figura 4.26).
En efecto, cuando los profesores lo presentan simplemente como otra cosa para memorizar, ¿quién puede culpar a los estudiantes? En realidad, ambas parcelas tienen como objetivo simplificar la determinación de parámetros, tales como\(K_m\) y\(V_{max}\). Al hacer cualquiera de estas gráficas modificadas, es importante reconocer que se utilizan los mismos datos que en la elaboración de una gráfica V0 vs. [S]. Los datos son simplemente manipulados para facilitar el trazado.
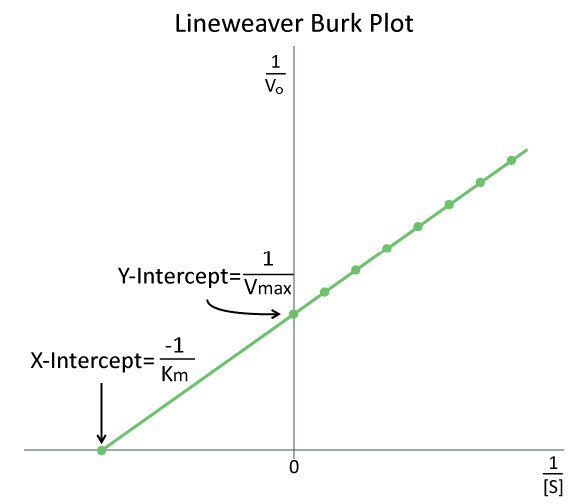
Figura 4.26 - Una gráfica Lineweaver-Burk de\(1/V_0\) vs\(1/[S]\). Imagen de Aleia Kim
Doble recíproco
Para una gráfica Lineweaver-Burk, la manipulación es utilizando el recíproco de los valores tanto de la velocidad como de la concentración de sustrato. Los valores invertidos se representan luego en una gráfica como 1/V0 vs. 1/ [S]. Debido a estas inversiones, las parcelas Lineweaver-Burk se denominan comúnmente parcelas de “doble reciprocidad”. Como puede verse en la Figura 4.26, el valor de Km en una gráfica Lineweaver Burk se determina fácilmente como el recíproco negativo de la intercepción x, mientras que la Vmax es la inversa de la intercepción y. Otra manipulación relacionada de datos cinéticos incluyen diagramas de Eadie-Hofstee, que grafica V0 vs V0/ [S] y da Vmax como la intercepción del eje Y con la pendiente de la línea siendo -Km.
Molecularidad de las reacciones
El término molecularidad se refiere al número de moléculas que deben unirse para que se produzca una reacción. Las reacciones del tipo A -> B (donde 'A' es el reactivo y 'B' es el producto) son unimoleculares, ya que A se cambia directamente a B. La velocidad de la reacción se relaciona solo con la concentración de reactivo A. Para una reacción bimolecular donde A + B C la reacción depende de la concentración tanto de A como de B y su tasa estará relacionada con el producto de la concentración de A y de B.
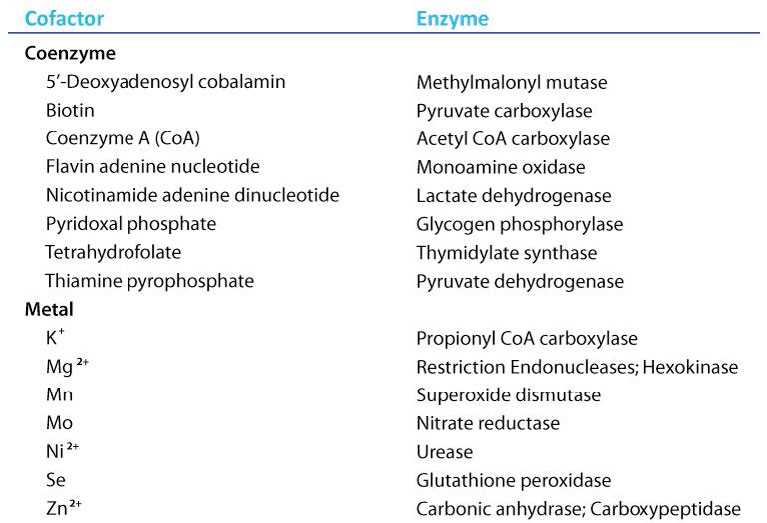
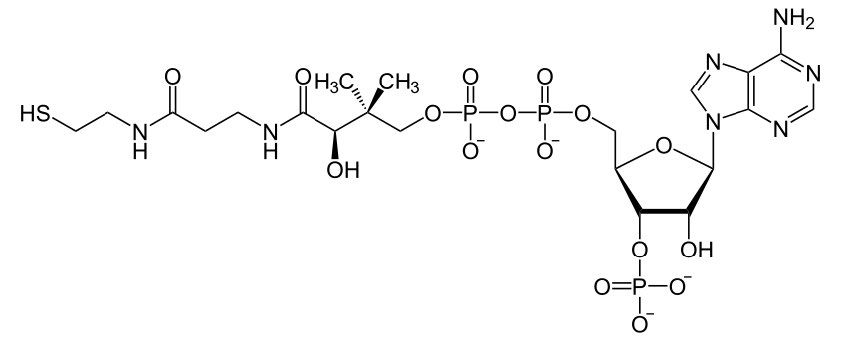
Coenzimas
Las moléculas orgánicas que ayudan a las enzimas y facilitan la catálisis son cofactores llamados coenzimas. El término cofactor es una categoría amplia generalmente subdividida en iones inorgánicos y coenzimas. Si la coenzima está unida de manera muy estrecha o covalente a la enzima, se le conoce como un grupo protésico. Las enzimas sin sus cofactores son inactivas y se denominan apoenzimas. Las enzimas que contienen todos sus cofactores se llaman holoenzimas.
Estudios cinéticos preestables
En el estudio de las tasas cinéticas de las reacciones enzimáticas, el tiempo cero es un punto muy crítico. Se establece cuándo comienza la mezcla del sustrato con la enzima y la medición de la formación del producto. En el tiempo cero, no hay producto. Como se muestra en la Figura 4.29, la apariencia del producto (en una escala de tiempo corta) pasa por una fase de estallido temprano con una pendiente pronunciada para [producto] /tiempo y luego cambia.
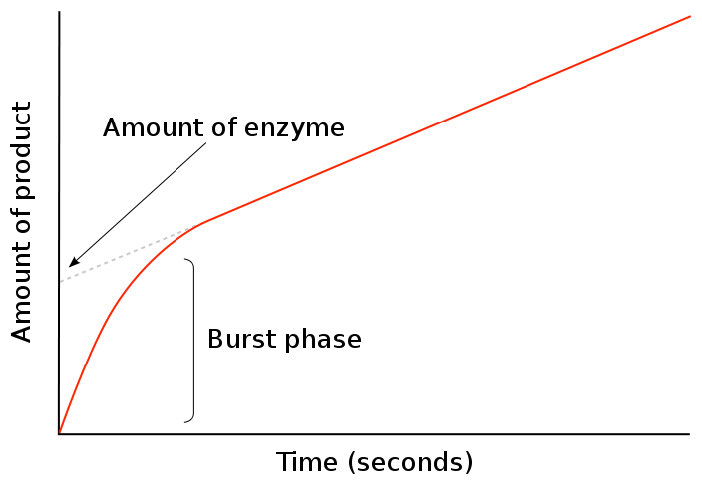
Figura 4.29 - Fase de estallido de la formación del producto
Este cambio ocurre durante un periodo crítico en una reacción enzimática y da información sobre la velocidad de los ciclos de reacción. La duración de la fase de estallido indica cuánto tiempo ocurre una sola renovación de reacción, mientras que la lenta de la fase de post-estallido de la línea indica la cantidad de enzima “funcional” que realiza la reacción.
Después de la fase de estallido, disminuye la pendiente de la línea de la cantidad de producto frente al tiempo. Esto se debe a que la reacción entró en condiciones de estado estacionario, utilizadas para estudiar la cinética de Michaelis-Menten. En condiciones de estado estacionario, la cantidad del complejo enzima-sustrato (ES) es relativamente constante a lo largo del tiempo. En términos simples, esto ocurre cuando la velocidad de formación del complejo ES es igual a la tasa de conversión del sustrato en producto por la enzima con liberación del producto.
Acontecimientos anteriores
Los eventos que ocurren antes de las condiciones de estado estacionario se denominan estado preestacionario. Dependiendo de la enzima, en tan solo unos milisegundos, las condiciones de estado estacionario pueden estar presentes, lo que significa que si se espera estudiar la formación de intermedios de reacción en estado preestacionario, las herramientas para este análisis deben trabajar muy rápidamente. Un instrumento comúnmente utilizado para estudiar la cinética de estado estacionario se llama instrumento de flujo detenido.
Carga una solución enzimática y un sustrato en jeringas separadas cuya salida apunta hacia una cámara de mezcla. Las soluciones se mezclan rápidamente y comienzan las mediciones de la concentración del producto. Con un instrumento de flujo detenido, se pueden lograr tiempos muertos (tiempo entre la mezcla y la detección) de tan solo 0.3 mseg.

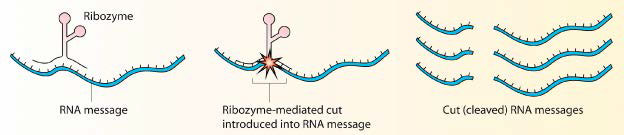
Ribozimas
Las proteínas no tienen el monopolio de actuar como catalizadores biológicos. Algunas moléculas de ARN también son capaces de acelerar las reacciones. La más famosa de estas moléculas fue descubierta por Tom Cech a principios de la década de 1980. Estudiando la escisión de un intrón en Tetrahymena, Cech estaba desconcertado ante su incapacidad para encontrar proteínas que catalizaran el proceso. En última instancia, se reconoció que la catálisis provenía del intrón mismo. Fue un ARN autoempalmado y desde entonces, se han encontrado muchos otros ejemplos de ARN catalíticos. Las moléculas catalíticas de ARN se conocen como ribozimas.
 359
359
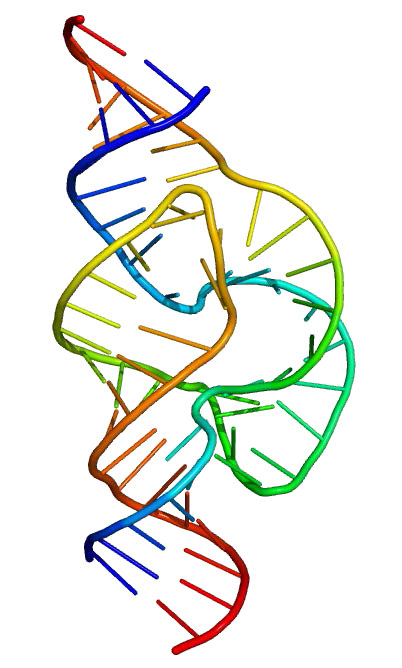
No es inusual
Las ribozimas, sin embargo, no son raridades de la naturaleza. Los ribosomas productores de proteínas de las células son esencialmente ribozimas gigantes. El ARNr 23S del ribosoma procariota y el ARNr 28S del ribosoma eucariota catalizan la formación de enlaces peptídicos.
Las ribozimas también son importantes en nuestra comprensión de la evolución de la vida en la Tierra. Se ha demostrado que son capaces a través de la selección para evolucionar la autorreplicación. De hecho, las ribozimas realmente responden a un dilema de pollo/huevo -que vino primero, enzimas que hacen el trabajo de la célula o ácidos nucleicos que portan la información requerida para producir las enzimas. Como portadores de información genética y catalizadores, las ribozimas son probablemente tanto el pollo como el huevo en el origen de la vida.


