5.3: Crecimiento y Regulación de la Población
- Page ID
- 54241
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los ecologistas poblacionales utilizan diversos métodos para modelar la dinámica poblacional. Un modelo preciso debe ser capaz de describir los cambios que ocurren en una población y predecir cambios futuros. Los dos modelos más simples de crecimiento poblacional utilizan ecuaciones deterministas (ecuaciones que no dan cuenta de eventos aleatorios) para describir la tasa de cambio en el tamaño de una población a lo largo del tiempo. El primero de estos modelos, el crecimiento exponencial, describe poblaciones que aumentan en número sin ningún límite para su crecimiento. El segundo modelo, el crecimiento logístico, introduce límites al crecimiento reproductivo que se vuelven más intensos a medida que aumenta el tamaño de la población. Ninguno de los modelos describe adecuadamente a las poblaciones naturales, pero proporcionan puntos de comparación.
La tasa de crecimiento poblacional (r)
La tasa de crecimiento poblacional (a veces llamada tasa de aumento o tasa de crecimiento per cápita, r) es igual a la tasa de natalidad (b) menos la tasa de mortalidad (d) dividida por el tamaño inicial de la población (N 0).
Otro método para calcular la tasa de crecimiento poblacional involucra el tamaño final e inicial de la población (cifra\(\PageIndex{a}\)). En este caso, la tasa de crecimiento poblacional (r) es igual al tamaño final de la población (N) menos el tamaño inicial de la población (N 0) y dividido por el tamaño inicial de la población (N 0).

Tiempo de Duplicación
El tiempo de duplicación es cuánto tardará una población en llegar a duplicar su tamaño inicial. El tiempo de duplicación (t) es igual a 0.69 dividido por la tasa de crecimiento poblacional (r), escrito como proporción.
Los ecologistas poblacionales a veces redondean esta ecuación y calculan el tiempo de duplicación utilizando la “Regla de 70" (dividiendo 70 por la tasa de crecimiento poblacional, escrita como porcentaje). Para expresar la tasa de crecimiento poblacional como porcentaje, se multiplica por 100%. Así, el 0.69 en la ecuación original del tiempo de duplicación también se multiplica por 100. Este valor (69) se redondea a 70 por simplicidad.
Crecimiento Exponencial
Charles Darwin, al desarrollar su teoría de la selección natural, fue influenciado por el clérigo inglés Thomas Malthus. Malthus publicó su libro en 1798 afirmando que las poblaciones con abundantes recursos naturales crecen muy rápidamente. Sin embargo, limitan un mayor crecimiento al agotar sus recursos. El patrón temprano de acelerar el tamaño de la población se llama crecimiento exponencial (figura\(\PageIndex{b}\)).
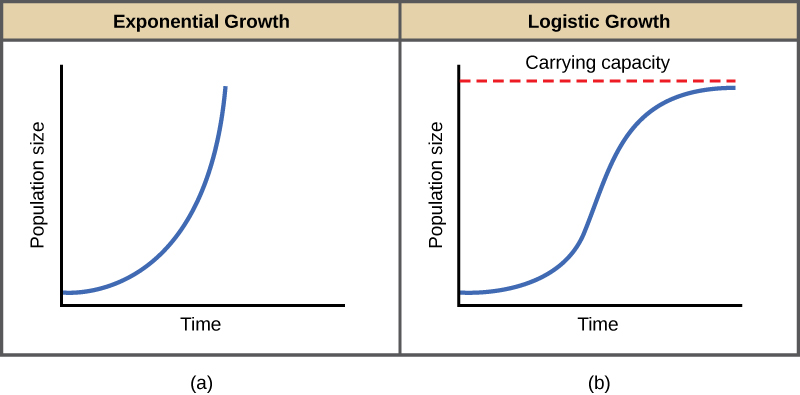
El mejor ejemplo de crecimiento exponencial en organismos se observa en bacterias. Las bacterias son procariotas que se reproducen rápidamente, alrededor de una hora para muchas especies. Si se colocan 1000 bacterias en un matraz grande con abundante aporte de nutrientes (por lo que los nutrientes no se agotarán rápidamente), el número de bacterias se habrá duplicado de 1000 a 2000 después de apenas una hora (cifra\(\PageIndex{c}\)). En otra hora, cada una de las 2000 bacterias se dividirá, produciendo 4000 bacterias. Después de la tercera hora, debería haber 8000 bacterias en el matraz. El concepto importante de crecimiento exponencial es que la tasa de crecimiento —el número de organismos añadidos en cada generación reproductiva— está aumentando en sí misma; es decir, el tamaño de la población está aumentando a un ritmo cada vez mayor. Después de 24 de estos ciclos, la población habría aumentado de 1000 a más de 16 mil millones de bacterias. Cuando el tamaño de la población, N, se traza a lo largo del tiempo, se produce una curva de crecimiento en forma de J (figura\(\PageIndex{b}\)).

El ejemplo de bacterias en un matraz no es realmente representativo del mundo real donde los recursos suelen ser limitados. Sin embargo, cuando una especie se introduce en un nuevo hábitat que encuentra adecuado, puede mostrar un crecimiento exponencial por un tiempo. En el caso de las bacterias en el matraz, algunas bacterias morirán durante el experimento y así no se reproducirán; por lo tanto, la tasa de crecimiento se reduce de una tasa máxima en la que no hay mortalidad.
Crecimiento Logístico
El crecimiento exponencial extendido sólo es posible cuando se dispone de infinitos recursos naturales; este no es el caso en el mundo real. Charles Darwin reconoció este hecho en su descripción de la “lucha por la existencia”, que establece que los individuos competirán, con miembros de su propia u otra especie, por recursos limitados. Los exitosos tienen más probabilidades de sobrevivir y transmitir los rasgos que los hicieron exitosos a la siguiente generación a un ritmo mayor (selección natural). Para modelar la realidad de los recursos limitados, los ecologistas poblacionales desarrollaron el modelo de crecimiento logístico.
En el mundo real, con sus limitados recursos, el crecimiento exponencial no puede continuar indefinidamente. El crecimiento exponencial puede ocurrir en entornos donde hay pocos individuos y abundantes recursos, pero cuando el número de individuos sea lo suficientemente grande, los recursos se agotarán y la tasa de crecimiento disminuirá. Eventualmente, la tasa de crecimiento se estancará o se nivelará (cifra\(\PageIndex{b}\)). Este tamaño poblacional, que está determinado por el tamaño máximo de población que puede sostener un ambiente en particular, se denomina capacidad de carga, simbolizada como K. En poblaciones reales, una población en crecimiento suele rebasar su capacidad de carga y la tasa de mortalidad aumenta más allá de la tasa de natalidad provocando que el tamaño de la población disminuya de nuevo a la capacidad de carga o por debajo de ella La mayoría de las poblaciones suelen fluctuar alrededor de la capacidad de carga de manera ondulada en lugar de existir justo en ella.
Una gráfica de crecimiento logístico produce la curva en forma de S (figura\(\PageIndex{b}\)). Se trata de un modelo más realista de crecimiento poblacional que de crecimiento exponencial. Hay tres secciones diferentes a una curva en forma de S. Inicialmente, el crecimiento es exponencial porque hay pocos individuos y amplios recursos disponibles. Entonces, a medida que los recursos comienzan a limitarse, la tasa de crecimiento disminuye. Finalmente, la tasa de crecimiento se nivela en la capacidad de carga del ambiente, con poco cambio en el número de población a lo largo del tiempo.
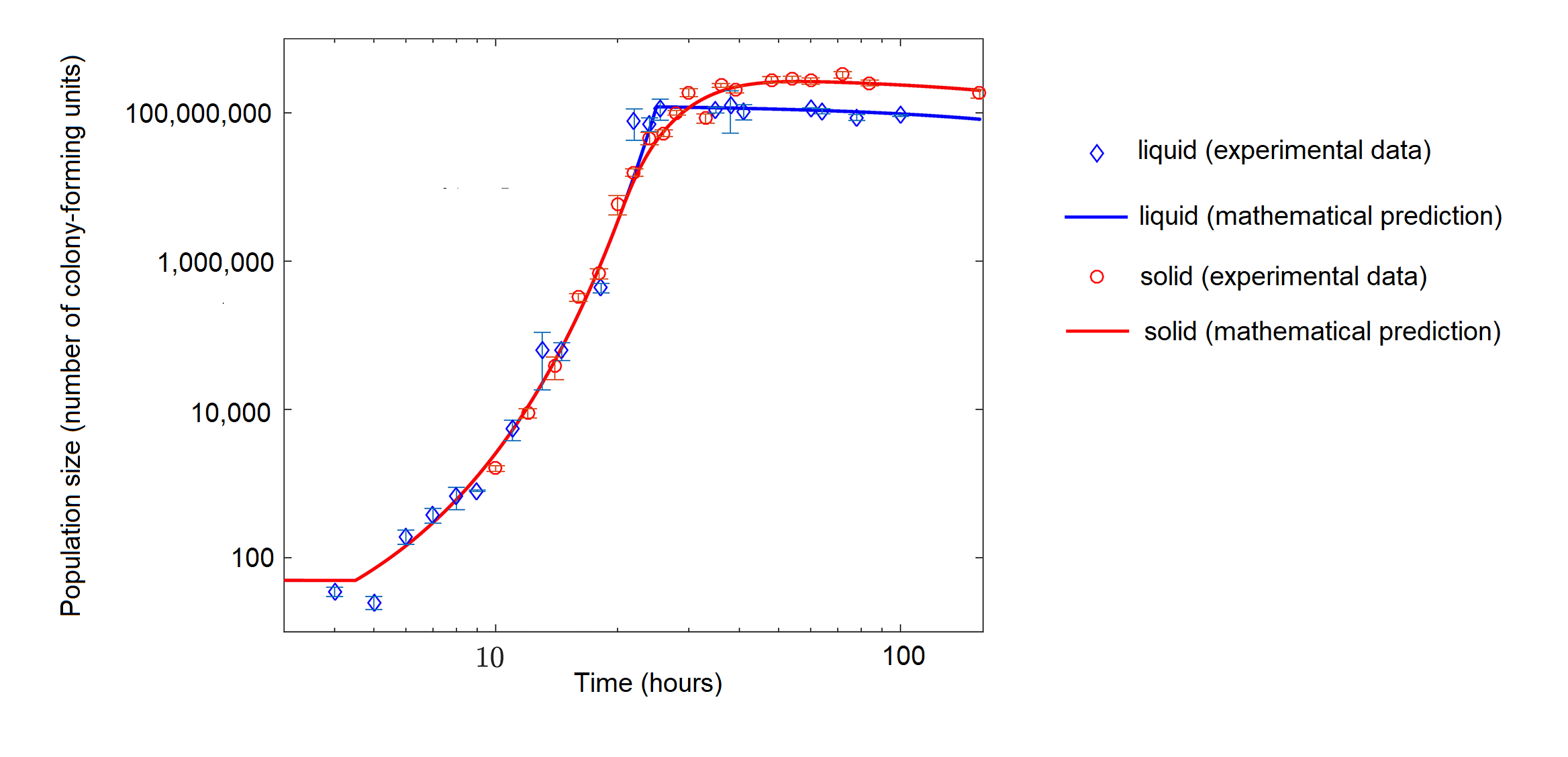
Mientras que las bacterias en un matraz con abundantes nutrientes podrían exhibir inicialmente un crecimiento exponencial, las bacterias cultivadas con nutrientes limitados pueden exhibir crecimiento logístico (figura\(\PageIndex{d}\)).
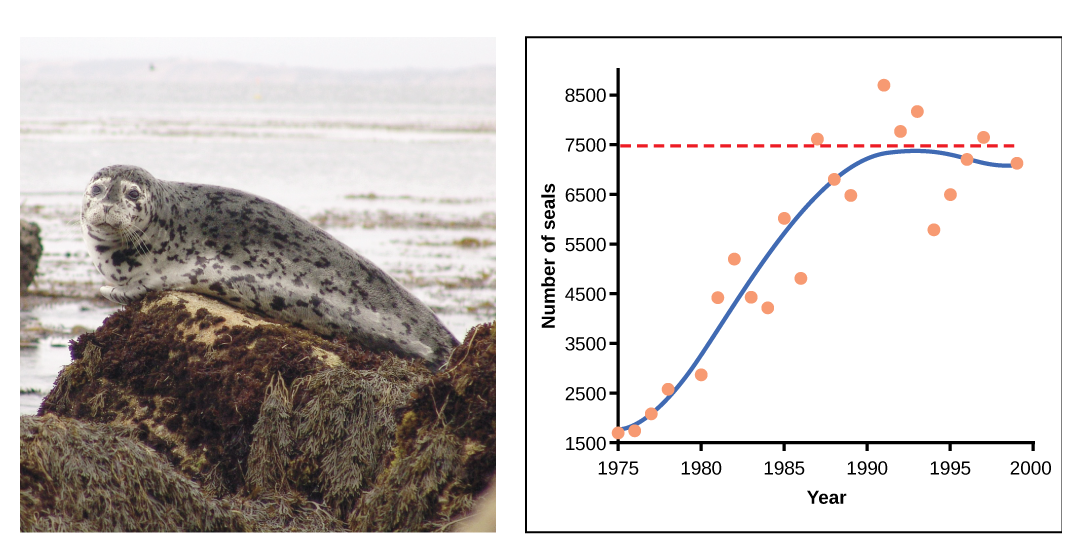
En algunas poblaciones, hay variaciones a la curva en forma de S. Los ejemplos en poblaciones silvestres incluyen ovejas y focas de puerto (figura\(\PageIndex{e}\)). En ambos ejemplos, el tamaño de la población supera la capacidad de carga por cortos periodos de tiempo y luego cae por debajo de la capacidad de carga posteriormente. Esta fluctuación en el tamaño de la población continúa ocurriendo a medida que la población oscila alrededor de su capacidad de carga. Aún así, incluso con esta oscilación se confirma el modelo logístico.
El modelo logístico de crecimiento poblacional no es la única manera en que las poblaciones responden a recursos limitados. En algunas poblaciones, el crecimiento es exponencial hasta que los recursos se agotan, se acumulan desechos o se propaga la enfermedad (ver factores limitantes a continuación), y la población luego se estrella. Así, la tasa de crecimiento de la población (y el tamaño) pueden caer en picado rápidamente en lugar de disminuir a medida que se acerca a la capacidad de carga.
Dinámica y Regulación Poblacional
El modelo logístico de crecimiento poblacional, si bien es válido en muchas poblaciones naturales y un modelo útil, es una simplificación de la dinámica poblacional del mundo real. Implícito en el modelo es que la capacidad de carga del entorno no cambia, lo que no es el caso. La capacidad de carga varía anualmente. Por ejemplo, algunos veranos son calurosos y secos mientras que otros son fríos y húmedos; en muchas zonas, la capacidad de carga durante el invierno es mucho menor que durante el verano. Además, algunos factores (factores de crecimiento) aumentan la tasa de crecimiento poblacional mientras que otros factores (factores limitantes) ralentizan el crecimiento poblacional. Ejemplos de factores de crecimiento son los recursos como la comida, el agua y el espacio. Los factores limitantes pueden clasificarse como dependientes de la densidad o independientes de la densidad.
Regulación dependiente de la densidad
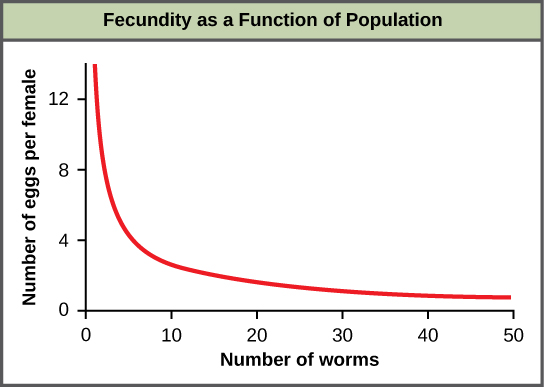
La mayoría de los factores dependientes de la densidad son de naturaleza biológica (bióticos). Por lo general, cuanto más densa es una población, mayor es su tasa de mortalidad. Un ejemplo de regulación dependiente de la densidad se muestra en la figura\(\PageIndex{f}\) con resultados de un estudio centrado en la lombriz intestinal gigante (Ascaris lumbricoides), un parásito de humanos y otros mamíferos. Las poblaciones más densas del parásito presentaron menor fecundidad: contenían menos huevos. Una posible explicación para esto es que las hembras serían más pequeñas en poblaciones más densas (debido a los recursos limitados) y que las hembras más pequeñas tendrían menos huevos. Esta hipótesis fue probada y desmentida en un estudio de 2009 que demostró que el peso femenino no tuvo influencia. La causa real de la densidad-dependencia de la fecundidad en este organismo aún no está clara y a la espera de una mayor investigación.
Los factores dependientes de la densidad incluyen depredación, parasitismo, herbivoría, competencia y acumulación de desechos. A medida que aumenta una población, sus depredadores son capaces de cosecharla con mayor facilidad. La densidad de presas también afecta la tasa de crecimiento poblacional de los depredadores: la baja densidad de presas aumenta la mortalidad de su depredador porque tiene más dificultades para localizar sus fuentes de alimento.
Los parásitos son capaces de pasar de hospedador a hospedador más fácilmente a medida que aumenta la densidad poblacional del huésped. Por esta razón, las epidemias entre los humanos son particularmente severas en las ciudades. De hecho, durante la mayor parte del período desde que los humanos comenzaron a vivir en las ciudades, las poblaciones de las ciudades se han mantenido sólo a través de la inmigración continua del campo. No hasta el desarrollo de saneamiento comunitario, inmunización y otras medidas de salud pública las ciudades evitaron caídas bruscas periódicas de población como consecuencia de epidemias. Las epidemias recurrentes de la “muerte negra” en Europa que comenzaron en el siglo XIV provocaron una fuerte disminución de la población. En solo tres años (1348—1350), al menos una cuarta parte de la población de Europa murió a causa de la enfermedad (probablemente peste).
De manera similar, los herbívoros pueden propagarse más fácilmente entre plantas individuales en una población densa. Es por ello que el cultivo en tiras (ver Agricultura Sustentable) ayuda a controlar las plagas. Un herbívoro o patógeno vegetal puede infectar una hilera de plantas, pero es menos probable que se propague a hileras más distantes de esa especie.
Si bien la competencia interespecífica ocurre entre diferentes especies, la competencia intraespecífica ocurre cuando miembros de la misma especie se dañan entre sí al usar los mismos recursos. Por ejemplo, en el verano de 1980, gran parte del sur de Nueva Inglaterra fue golpeada por una infestación de la polilla gitana (figura\(\PageIndex{g}\)). A medida que avanzaba el verano, las larvas (orugas) puparon, los adultos eclosionados se aparearon, las hembras pusieron masas de huevos (cada masa contenía varios cientos de huevos) en prácticamente todos los árboles de la región. A principios de mayo de 1981, las orugas jóvenes que eclosionaron de estos huevos comenzaron a alimentarse y a mudar.

Los resultados fueron dramáticos: En 72 horas, un árbol de haya de 50 pies o un pino blanco de 25 pies quedaría completamente defoliado. Grandes parches de bosque comenzaron a tomar una apariencia invernal con sus esqueletos de ramas desnudas. De hecho, la infestación fue tan pesada que muchos árboles quedaron completamente defoliados antes de que las orugas pudieran completar su desarrollo larvario. El resultado: una muerte masiva de los animales; muy pocos lograron completar la metamorfosis. Aquí, entonces, fue un ejemplo dramático de cómo la competencia entre miembros de una especie por un recurso finito -en este caso, la comida - provocó una fuerte caída de la población. El efecto fue claramente dependiente de la densidad. Las menores densidades poblacionales del verano anterior habían permitido que la mayoría de los animales completaran su ciclo de vida.
Regulación independiente de la densidad
Los factores independientes de la densidad, típicamente de naturaleza física o química (abióticos), influyen en la mortalidad de una población independientemente de su densidad, incluyendo el clima (figura\(\PageIndex{h}\)), los desastres naturales (terremotos, volcanes, incendios, etc.) y la contaminación. Un ciervo individual puede morir en un incendio forestal independientemente de cuántos venados se encuentren en esa zona. Sus posibilidades de supervivencia son las mismas tanto si la densidad poblacional es alta como baja. Lo mismo ocurre con el clima frío de invierno.

En situaciones de la vida real, la regulación poblacional es muy complicada y los factores dependientes de la densidad e independientes pueden interactuar. Una población densa que se reduce de manera independiente de la densidad por algún factor (s) ambiental (s) podrá recuperarse de manera diferente a una población dispersa. Por ejemplo, una población de venados afectados por un duro invierno se recuperará más rápido si quedan más venados por reproducirse.
Atribuciones
Modificado por Melissa Ha de las siguientes fuentes:
- Crecimiento poblacional y regulación desde la biología ambiental por Matthew R. Fisher (CC-BY)
- Principios del crecimiento poblacional y La población humana desde la biología por John W. Kimball (CC-BY)
- Dinámica poblacional y regulación de la biología general por OpenStax (CC-BY)


