5.4: Historia de vida

Las características de la historia de vida, son aquellas que se relacionan con la supervivencia, mortalidad y reproducción de una especie. Los ejemplos incluyen las tasas de natalidad, la edad en la primera reproducción, el número de crías y las tasas de mortalidad. Estas características evolucionan igual que los rasgos físicos o el comportamiento, lo que lleva a adaptaciones que afectan el crecimiento de la población.

Estrategias Reproductivas

Los ecologistas poblacionales han planteado la hipótesis de que conjuntos de características pueden evolucionar en especies que conducen a adaptaciones particulares a sus entornos. Estas adaptaciones impactan el tipo de crecimiento poblacional que experimentan sus especies. Los ecologistas poblacionales han descrito un continuo de “estrategias” de historia de vida con especies seleccionadas por K en un extremo y especies seleccionadas r en el otro (tabla\(\PageIndex{a}\)). Las especies seleccionadas por K se adaptan a ambientes estables y predecibles. Las poblaciones de especies seleccionadas por K tienden a existir cerca de su capacidad de carga (que se representa con la letra “K” en la ecuación para el crecimiento logístico de la población). Estas especies tienden a tener descendencia más grande, pero menor, aportan grandes cantidades de recursos a cada descendencia, y tienen largos tiempos de generación. Los elefantes serían un ejemplo de una especie seleccionada por K (figura\(\PageIndex{a}\)). Cuando un hábitat se llena de una colección diversa de criaturas que compiten entre sí por las necesidades de la vida, la ventaja cambia a K -estrategas. Los estrategas K tienen poblaciones estables cercanas a K. No hay nada que ganar de una alta tasa de crecimiento (r). La especie se beneficiará más por una adaptación cercana a las condiciones de su entorno.

Tabla\(\PageIndex{a}\): Comparación de especies seleccionadas por K y r

Características de las especies seleccionadas por K	Características de las especies seleccionadas por r
Maduras tardías	Maduras tempranas
Mayor longevidad	Menor longevidad
Aumento de la atención parental	Disminución del cuidado parental
Competidores fuertes	Competidores débiles (colonizadores fuertes)
Menos crías	Más descendencia
Cría más grande	Cría más pequeña

Figura\(\PageIndex{a}\): (a) Los elefantes son considerados especies seleccionadas por K, ya que viven mucho tiempo, maduran tarde y brindan cuidados parentales a largo plazo a pocas crías. Los encinos producen muchas crías que no reciben cuidado parental, pero se consideran especies seleccionadas por K en función de la longevidad y maduración tardía. b) Los dientes de león y las medusas se consideran especies seleccionadas por r, ya que maduran temprano, tienen una vida útil corta y producen muchas crías que no reciben cuidado parental.

Las especies seleccionadas por r se adaptan a ambientes inestables e impredecibles. Tienen un gran número de crías pequeñas. Los animales seleccionados por r no proporcionan muchos recursos ni cuidado parental a la descendencia, y las crías son relativamente autosuficientes al nacer. Ejemplos de especies seleccionadas por r son invertebrados marinos como medusas y plantas como el diente de león (figura\(\PageIndex{a}\)). Los r- estrategas tienen períodos de vida cortos y se reproducen rápidamente, lo que resulta en tiempos de generación cortos. Por ejemplo, la mosca doméstica puede producir 7 generaciones cada año (cada una de aproximadamente 120 jóvenes). La ragweed está bien adaptada para explotar su entorno a toda prisa, antes de que los competidores puedan establecerse. Crece rápidamente y produce una gran cantidad de semillas (después de liberar su polen, la perdición de muchos enfermos de fiebre del heno). Debido a que el enfoque de la ragweed para la supervivencia continua es a través de la reproducción rápida (un alto valor de r) se le llama r -estratega. Otras malezas, muchos insectos y muchos roedores también son r -estrategas. Si de hecho, si consideramos a un organismo una plaga, probablemente sea un r -estratega.

Las dos estrategias extremas se encuentran en dos extremos de un continuo en el que existirán historias de vida de especies reales. Además, las estrategias de historia de vida no necesitan evolucionar como suites sino que pueden evolucionar independientemente unas de otras; por lo tanto, cada especie puede tener algunas características que tienden hacia un extremo u otro. Sin embargo, la teoría de la selección r y K proporciona una base para un marco de historia de vida más preciso. Se han desarrollado nuevos modelos demográficos de evolución de la historia de vida, que incorporan muchos conceptos ecológicos incluidos en la teoría de la selección r y K, así como la estructura de edad de la población y los factores de mortalidad.

Mesas de Vida

Las tablas de vida proporcionan información importante sobre la historia de vida de un organismo y la esperanza de vida de los individuos a cada edad. Se modelan a partir de tablas actuariales utilizadas por la industria aseguradora para estimar la esperanza de vida humana. Las tablas de vida pueden incluir la probabilidad de que cada grupo de edad muera antes de su próximo cumpleaños, el porcentaje de individuos sobrevivientes que mueren en un intervalo de edad determinado (su tasa de mortalidad y su esperanza de vida en cada intervalo). Un ejemplo de una tabla de vida se muestra en Tabla\(\PageIndex{b}\) de un estudio de ovejas de montaña Dall, una especie nativa del noroeste de América del Norte. Observe que la población se divide en intervalos de edad (columna A).

Como se puede observar a partir de los datos de la tasa de mortalidad (columna D), se produjo una alta tasa de mortalidad cuando las ovejas tenían entre seis meses y un año de edad, y luego aumentó aún más de 8 a 12 años, después de lo cual hubo pocos sobrevivientes. Los datos indican que si una oveja de esta población sobreviviera hasta la edad de uno, podría esperarse que viviera otros 7.7 años en promedio, como lo muestran los números de esperanza de vida en la columna E. Las tablas de vida suelen incluir más información que la mostrada en la Tabla\(\PageIndex{b}\), como las tasas de fecundidad (reproducción) para cada grupo de edad.

Tabla\(\PageIndex{b}\): Tabla de Vida de Ovejas de Montaña Dall

Intervalo de edad (años)	Número que muere en el intervalo de edad de 1000 nacidos	Número que sobrevive al inicio del intervalo de edad de 1000 nacidos	Tasa de mortalidad por 1000 vivos al inicio del intervalo de edad	Esperanza de vida o media de vida restante para quienes alcanzan el intervalo de edad
0—0.5	54	1000	54.0	7.06
0.5—1	145	946	153.3	—
1—2	12	801	15.0	7.7
2—3	13	789	16.5	6.8
3—4	12	776	15.5	5.9
4—5	30	764	39.3	5.0
5—6	46	734	62.7	4.2
6—7	48	688	69.8	3.4
7—8	69	640	107.8	2.6
8—9	132	571	231.2	1.9
9—10	187	439	426.0	1.3
10—11	156	252	619.0	0.9
11—12	90	96	937.5	0.6
12—13	3	6	500.0	1.2
13—14	3	3	1000	0.7

Curvas de supervivencia

Otra herramienta utilizada por los ecologistas poblacionales es una curva de supervivencia, que es una gráfica del número de individuos que sobreviven en cada intervalo de edad versus tiempo. Estas curvas permiten comparar las historias de vida de diferentes poblaciones (figura\(\PageIndex{c}\)). Existen tres tipos de curvas de supervivencia. En una curva de supervivencia tipo I, la mortalidad es baja en los primeros y medianos años y ocurre principalmente en individuos mayores. Los organismos que presentan una supervivencia tipo I suelen producir pocas crías y proporcionan un buen cuidado a la descendencia aumentando la probabilidad de su supervivencia. Los humanos y la mayoría de los mamíferos presentan una curva de supervivencia tipo I. En las curvas de supervivencia tipo II, la mortalidad es relativamente constante a lo largo de toda la vida, y es igualmente probable que la mortalidad ocurra en cualquier momento de la vida. Muchas poblaciones de aves proporcionan ejemplos de una curva de supervivencia intermedia o tipo II. En las curvas de supervivencia tipo III, las edades tempranas experimentan la mayor mortalidad con tasas de mortalidad mucho menores para los organismos que llegan a años avanzados. Los organismos de tipo III suelen producir un gran número de crías, pero proporcionan muy poco o ningún cuidado para ellos. Los árboles e invertebrados marinos presentan una curva de supervivencia tipo III debido a que muy pocos de estos organismos sobreviven en su juventud, pero aquellos que llegan a la vejez tienen más probabilidades de sobrevivir por un período de tiempo relativamente largo.

Figura\(\PageIndex{c}\): Las curvas de supervivencia muestran la probabilidad de supervivencia en una población según la edad. El número de individuos que sobreviven (en una escala logarítmica) está en el eje y, y el tiempo (que representa la edad relativa) está en el eje x. Los humanos y la mayoría de los mamíferos tienen una curva de supervivencia Tipo I, ya que la muerte ocurre principalmente en los años mayores. La curva de supervivencia Tipo I está representada por una curva convexa, que disminuye rápidamente al final. Las aves tienen una curva de supervivencia Tipo II, ya que la muerte a cualquier edad es igualmente probable. La curva de supervivencia Tipo II está representada por una línea recta, que va desde la parte superior izquierda hasta la parte inferior derecha de la gráfica. Los árboles tienen una curva de supervivencia Tipo III porque muy pocos sobreviven en los años más jóvenes, pero después de cierta edad, los individuos son mucho más propensos a sobrevivir. La curva de supervivencia Tipo III está representada por una curva cóncava, que inicialmente disminuye rápidamente y luego se aplana.

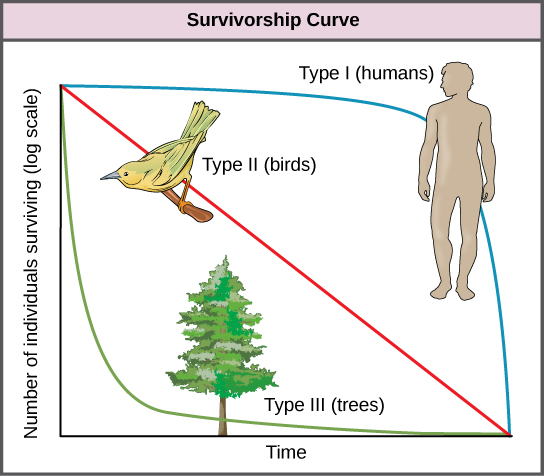
Si bien no existe una asociación exacta entre las estrategias reproductivas (seleccionadas por K o r) y las curvas de supervivencia (Tipo I, II o III), las especies seleccionadas por K tienen más probabilidades de tener una curva de supervivencia de Tipo III. Las especies seleccionadas por r tienden a tener una curva de supervivencia Tipo I.

Atribución

Modificado por Melissa Ha de las siguientes fuentes:

• Dinámica poblacional y regulación de la biología general por OpenStax (CC-BY)
• Demografía y dinámica poblacional desde la biología ambiental por Matthew R. Fisher (CC-BY)
• Principios del crecimiento poblacional desde la biología por John W. Kimball (CC-BY)