6.3: Canales alámbricos

Objetivos de aprendizaje

• El análisis y las características de transferencia de los canales alámbricos.

Los canales alámbricos fueron los primeros utilizados para las comunicaciones eléctricas a mediados del siglo XIX para el telégrafo. Aquí, el canal es uno de varios cables que conectan el transmisor al receptor. El transmisor simplemente crea un voltaje relacionado con la señal del mensaje y lo aplica al (los) cable (s). Debemos tener un circuito, un camino cerrado, que admita el flujo de corriente. En el caso de las comunicaciones de un solo cable, la tierra se utiliza como ruta de retorno de la corriente. De hecho, el término tierra para el nodo de referencia en circuitos se originó en telégrafos de un solo cable. Se puede imaginar que las características eléctricas de la tierra son muy variables, y lo son. Los canales metálicos de un solo cable no pueden admitir una transmisión de señal de alta calidad que tenga un ancho de banda superior a unos pocos cientos de Hertz en

Figura 6.3.1 El cable coaxial consiste en un conductor envuelto alrededor del conductor central. Este tipo de cable admite señales de ancho de banda más amplio que el par trenzado, y encuentra uso en televisión por cable y Ethernet.

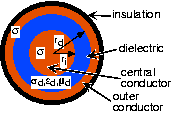
En consecuencia, la mayoría de los canales por cable hoy en día consisten esencialmente en pares de cables conductores (Figura 6.3.1), y el transmisor aplica un voltaje relacionado con el mensaje a través del par. La forma en que estos pares de cables están físicamente configurados afecta en gran medida sus características de transmisión. Un ejemplo es el par trenzado, en donde los cables están envueltos uno alrededor del otro. Los cables telefónicos son un ejemplo de un canal de par trenzado. Otro es el cable coaxial, donde un conductor concéntrico rodea un cable central con un material dieléctrico en el medio. El cable coaxial, llamado con cariño “co-ax” por los ingenieros, es lo que utiliza Ethernet como canal. En cualquier caso, los canales por cable forman un circuito dedicado entre el transmisor y el receptor. Como encontraremos posteriormente, varias transmisiones pueden compartir el circuito mediante técnicas de modulación de amplitud; la televisión por cable comercial es un ejemplo. Estos circuitos portadores de información están diseñados para minimizar la interferencia de fuentes electromagnéticas cercanas. Por lo tanto, en el momento en que las señales llegan al receptor, están relativamente libres de interferencias y ruido.

Tanto el par trenzado como el coaxial son ejemplos de líneas de transmisión, todas las cuales tienen el modelo de circuito que se muestra en la Figura para una longitud infinitesimalmente pequeña. Este modelo de circuito surge de resolver las ecuaciones de Maxwell para la geometría particular de la línea de transmisión.

Figura 6.3.2 El llamado modelo de parámetros distribuidos para cables de dos hilos tiene la estructura del modelo de circuito representado. Los valores de los elementos dependen de la geometría y las propiedades de los materiales utilizados para construir la línea de transmisión.

La resistencia en serie proviene del conductor utilizado en los cables y de la geometría del conductor. La inductancia y la capacitancia derivan de la geometría de la línea de transmisión, y la conductancia paralela del medio entre el par de cables. Tenga en cuenta que todos los elementos del circuito tienen valores expresados por el producto de una constante multiplicada por una longitud; esta notación representa que los valores de los elementos aquí tienen unidades por unidad de longitud. Por ejemplo, la resistencia en serie\[\widetilde{R} \nonumber \] tiene unidades de ohmios/metro. Para el cable coaxial, los valores de los elementos dependen del radio r _i del conductor interno, el radio exterior del dieléctrico r _d, la conductividad de los conductores σ, y la conductividad σ _d, la constante dieléctrica ε _d, y permitividad magnética μ _d del dieléctrico como

\[\widetilde{R}=\frac{1}{2\pi \delta \sigma }\left ( \frac{1}{r_{d}}+ \frac{1}{r_{i}}\right ) \nonumber \]

\[\widetilde{C}=\frac{2\pi \varepsilon _{d}}{\ln \left ( \frac{r_{d}}{r_{i}} \right )} \nonumber \]

\[\widetilde{G}=\frac{2(\pi ,\sigma _{d})}{\ln \left ( \frac{r_{d}}{r_{i}} \right )} \nonumber \]

\[\widetilde{L}=\frac{\mu _{d}}{2\pi }\ln \left ( \frac{r_{d}}{r_{i}} \right ) \nonumber \]

Para el par trenzado, que tiene una separación d entre los conductores que tienen conductividad σ y radio común r y que están sumergidos en un medio que tiene propiedades dieléctricas y magnéticas, los valores de los elementos son entonces

\[\widetilde{R}=\frac{1}{\pi r\delta \sigma } \nonumber \]

\[\widetilde{C}=\frac{\pi \varepsilon }{\arccos h\left ( \frac{d}{2r} \right )} \nonumber \]

\[\widetilde{G}=\frac{\pi \sigma }{\arccos h\left ( \frac{d}{2r} \right )} \nonumber \]

\[\widetilde{L}=\frac{\mu }{\pi }\left ( \frac{d}{2r}+\arccos h\left( \frac{d}{2r}\right )\right ) \nonumber \]

El voltaje entre los dos conductores y la corriente que fluye a través de ellos dependerá de la distancia x a lo largo de la línea de transmisión, así como del tiempo. Expresamos esta dependencia como v (x, t) e i (x, t). Cuando colocamos una fuente sinusoidal en un extremo de la línea de transmisión, estos voltajes y corrientes también serán sinusoidales porque el modelo de línea de transmisión consiste en elementos de circuito lineal. Como es habitual en el análisis de circuitos lineales, expresamos voltajes y corrientes como la parte real de señales exponenciales complejas, y escribimos variables de circuito como una amplitud compleja, aquí dependiente de la distancia, veces una exponencial compleja:

\[v(x,t)=\Re \left ( V(x)e^{i2\pi ft} \right ) \nonumber \]

\[i(x,t)=\Re \left ( I(x)e^{i2\pi ft} \right ) \nonumber \]

Usando el modelo de circuito de línea de transmisión, encontramos a partir de las relaciones KCL, KVL y v-i las ecuaciones que rigen las amplitudes complejas.

KCL en el nodo central

\[I(x)=I(x-\Delta (x))-V(x)(\widetilde{G}+i2\pi f\widetilde{C})\Delta (x) \nonumber \]

Relación V-I para la serie RL

\[V(x)-V(x+\Delta (x))=I(x)(\widetilde{R}+i2\pi f\widetilde{L})\Delta (x) \nonumber \]

Reorganizar y tomar el límite Δ (x) →0 produce las llamadas ecuaciones de línea de transmisión.

\[\frac{\mathrm{d} }{\mathrm{d} x}I(x)=-\left ( (\widetilde{G}+i2\pi f\widetilde{C})V(x) \right ) \nonumber \]

\[\frac{\mathrm{d} }{\mathrm{d} x}V(x)=-\left ( (\widetilde{R}+i2\pi f\widetilde{L})I(x) \right ) \nonumber \]

Al combinar estas ecuaciones, podemos obtener una única ecuación que gobierna cómo cambia la amplitud compleja de la tensión o la corriente con la posición a lo largo de la línea de transmisión. Tomando la derivada de la segunda ecuación y enchufando la primera ecuación en el resultado produce la ecuación que rige el voltaje.

\[\frac{\mathrm{d}^{2} }{\mathrm{d} x^{2}}V(x)= (\widetilde{G}+i2\pi f\widetilde{C})(\widetilde{R}+i2\pi f\widetilde{L})V(x) \nonumber \]

La solución de esta ecuación es

\[V(x)=V_{+}e^{-(\gamma x)}+V_{-}e^{\gamma x} \nonumber \]

Calcular su segunda derivada y comparar el resultado con nuestra ecuación para el voltaje puede verificar esta solución.

\[\frac{\mathrm{d} ^{2}}{\mathrm{d} x^{2}}V(x)=\gamma ^{2}\left ( V_{+}e^{-(\gamma x)}+V_{-}e^{\gamma x}\right ) \nonumber \]

\[\therefore \frac{\mathrm{d} ^{2}}{\mathrm{d} x^{2}}V(x)=\gamma ^{2}V(x) \nonumber \]

Nuestra solución funciona siempre y cuando la cantidad γ satisfaga

\[\gamma =\pm \left ( \sqrt{(\widetilde{G}+i2\pi f\widetilde{C})(\widetilde{R}+i2\pi f\widetilde{L})} \right ) \nonumber \]

\[\therefore \gamma =\pm (a(f)+ib(f)) \nonumber \]

Así, γ depende de la frecuencia, y la expresamos en términos de partes reales e imaginarias como se indica. Las cantidades V ₊ y V _- son constantes determinadas por la fuente y consideraciones físicas. Por ejemplo, que el origen espacial sea el centro del modelo de línea de transmisión en la Figura 6.3.2. Debido a que el modelo de circuito contiene elementos de circuito simples, las soluciones físicamente posibles para la amplitud de voltaje no pueden aumentar con la distancia a lo largo de la línea Expresar γ en términos de sus partes reales e imaginarias en nuestra solución muestra que tales aumentos son una posibilidad (matemática).

\[V(x)=V_{+}e^{(-(a+ib))x}+V_{-}e^{(a+ib)x} \nonumber \]

El voltaje no puede aumentar sin límite; debido a que a (f) siempre es positivo, debemos segregar la solución para x negativo y positivo. El primer término aumentará exponencialmente para x<0 a menos que V ₊ =0 en esta región; un resultado similar se aplica a V _- para x>0. Estas limitaciones físicas nos dan una solución más limpia.

\[V(x)=\begin{cases} V_{+}e^{(-(a+ib))x} & \text{ if } x> 0 \\ V_{-}e^{(a+ib)x} & \text{ if } x< 0 \end{cases} \nonumber \]

Esta solución sugiere que los voltajes (y las corrientes también) disminuirán exponencialmente a lo largo de una línea de transmisión. La constante de espacio, también conocida como constante de atenuación, es la distancia sobre la cual el voltaje disminuye en un factor de 1/e. Es igual al recíproco de a (f), que depende de la frecuencia, y es expresado por los fabricantes en unidades de dB/m.

La presencia de la parte imaginaria de γ, b (f), también proporciona una visión de cómo funcionan las líneas de transmisión. Debido a que la solución para x>0 es proporcional a e ^{- (ibx)}, sabemos que la amplitud compleja del voltaje variará sinusoidalmente en el espacio. La solución completa para el voltaje tiene la forma

\[v(x,t)=\Re \left ( V_{+}e^{-(ax)}e^{i(2\pi ft-bx)} \right ) \nonumber \]

La porción exponencial compleja tiene la forma de una onda propagadora. Si pudiéramos tomar una instantánea del voltaje (tomar su foto en _t=t1), veríamos una forma de onda sinusoidalmente variable a lo largo de la línea de transmisión. Un periodo de esta variación, conocido como la longitud de onda, es igual

\[\lambda =\frac{2\pi }{b} \nonumber \]

Si tuviéramos que tomar una segunda foto en algún momento posterior t=t _2, también veríamos una tensión sinusoidal.

Porque

\[2\pi ft_{2}-bx=2\pi f(t_{1}+t_{2}-t_{1})-bx=2\pi ft_{1}-b\left ( x-\frac{2\pi f}{b} (t_{2}-t_{1})\right ) \nonumber \]

la segunda forma de onda parece ser la primera, pero retrasada, desplazada hacia la derecha, en el espacio. Así, el voltaje pareció moverse hacia la derecha con una velocidad igual a

\[\frac{2\pi f}{b}\; where \; b> 0 \nonumber \]

Denotamos esta velocidad de propagación por c, y es igual

\[c-=\left | \frac{2\pi f}{\Im \left ( \sqrt{(\widetilde{G}+i2\pi f\widetilde{C})(\widetilde{R}+i2\pi f\widetilde{L})} \right )} \right | \nonumber \]

En la región de alta frecuencia donde

\[i2\pi f\widetilde{L}\geqslant \widetilde{R} \; and\; i2\pi f\widetilde{C}\geqslant \widetilde{G} \nonumber \]

la cantidad bajo el radical simplifica a

\[-4\left ( \pi ^{2} ,f^{2},\widetilde{L},\widetilde{C}\right ) \nonumber \]

y encontramos que la velocidad de propagación es

\[\lim_{f\rightarrow \infty }c=\frac{1}{\sqrt{\widetilde{L}\widetilde{C}}} \nonumber \]

Para el cable coaxial típico, esta velocidad de propagación es una fracción (de un tercio a dos tercios) de la velocidad de la luz.

Ejercicio\(\PageIndex{1}\)

Encuentre la velocidad de propagación en términos de parámetros físicos tanto para el cable coaxial como para los ejemplos de par trenzado.

Solución

En ambos casos, la respuesta depende menos de la geometría que de las propiedades del material. Para cable coaxial,

\[c=\frac{1}{\sqrt{\mu _{d}\varepsilon _{d}}} \nonumber \]

Para par trenzado,

\[c=\frac{1}{\sqrt{\mu \varepsilon }}\sqrt{\frac{\arccos h\left ( \frac{d}{2r} \right )}{\frac{\delta }{2r}+\arccos h\left ( \frac{d}{2r}\right )}} \nonumber \]

Mediante el uso de la segunda ecuación de la línea de transmisión desde arriba, podemos resolver para la amplitud compleja de la corriente. Considerando la región espacial x>0, por ejemplo, encontramos que

\[\frac{\mathrm{d} }{\mathrm{d} x}V(x)=-(\gamma V(x))=\left ( -(\widetilde{R}+i2\pi f\widetilde{L})I(x) \right ) \nonumber \]

lo que significa que la relación entre las amplitudes complejas de voltaje y corriente no depende de la distancia.

\[\frac{V(x)}{I(x)}=\sqrt{\frac{\widetilde{R}+i2\pi f\widetilde{L}}{\widetilde{G}+i2\pi f\widetilde{C}}} \nonumber \]

\[\frac{V(x)}{I(x)}=Z_{0} \nonumber \]

La cantidad Z ₀ se conoce como impedancia característica de la línea de transmisión. Obsérvese que cuando la frecuencia de la señal es suficientemente alta, la impedancia característica es real, lo que significa que la línea de transmisión aparece resistiva en este régimen de alta frecuencia.

\[\lim_{f\rightarrow \infty }Z_{0}=\sqrt{\frac{\widetilde{L}}{\widetilde{C}}} \nonumber \]

Los valores típicos para la impedancia característica son 50 y 75 Ω.

Una línea de transmisión relacionada es la fibra óptica. Aquí, el campo electromagnético es ligero, y se propaga por un cilindro de vidrio. En esta situación, no tenemos dos conductores —de hecho no tenemos ninguno— y la energía se propaga en lo que corresponde al material dieléctrico del cable coaxial. La comunicación por fibra óptica tiene exactamente las mismas propiedades que otras líneas de transmisión: La intensidad de la señal decae exponencialmente de acuerdo con la constante espacial de la fibra y se propaga a cierta velocidad menor que la luz en el espacio libre. Desde la perspectiva abarcadora de las ecuaciones de Maxwell, la única diferencia es la frecuencia de la señal electromagnética. Debido a que no hay conductores eléctricos presentes y la fibra está protegida por un “aislante” opaco, la transmisión de fibra óptica está libre de interferencias.

Ejercicio\(\PageIndex{1}\)

A partir de tablas de constantes físicas, encuentra la frecuencia de una sinusoide en el medio del rango de luz visible. Compara esta frecuencia con la de una señal de televisión por cable de frecuencia media.

Solución

Estas frecuencias se pueden encontrar en la tabla de asignación de espectro. La luz en el medio de la banda visible tiene una longitud de onda de aproximadamente 600 nm, lo que corresponde a una frecuencia de 5 × 10 ¹⁴ Hz. La televisión por cable transmite dentro de la misma banda de frecuencia que la televisión emitida (aproximadamente 200 MHz o 2 × 10 ⁸ Hz). Así, ¡las frecuencias electromagnéticas visibles son más de seis órdenes de magnitud mayores!

Para resumir, utilizamos líneas de transmisión para la comunicación de señales por cable de alta frecuencia. En la comunicación por cable, tenemos una conexión física directa, un circuito, entre el transmisor y el receptor. Cuando seleccionamos las características de la línea de transmisión y la frecuencia de transmisión para que operemos en el régimen de alta frecuencia, las señales no se filtran ya que se propagan a lo largo de la línea de transmisión: La impedancia característica es de valor real, la impedancia equivalente de la línea de transmisión es una resistencia, y todos los componentes de la señal a diversas frecuencias se propagan a la misma velocidad. La amplitud de la señal transmitida disminuye exponencialmente a lo largo de la línea de transmisión. Tenga en cuenta que en el régimen de alta frecuencia la constante de espacio es aproximadamente cero, lo que significa que la atenuación es bastante pequeña.

Ejercicio\(\PageIndex{1}\)

¿Cuál es el valor límite de la constante espacial en el régimen de alta frecuencia?

Solución

A medida que aumenta la frecuencia,

\[2\pi f\widetilde{C}\geqslant \widetilde{G}\; and \; 2\pi f\widetilde{L}\geqslant \widetilde{R} \nonumber \]

En esta región de alta frecuencia,

\[\gamma =i2\pi f\sqrt{\widetilde{L}\widetilde{C}}\sqrt{\left ( 1+\frac{\widetilde{G}}{i2\pi f\widetilde{C}} \right )\left ( 1+\frac{\widetilde{R}}{i2\pi f\widetilde{L}} \right )} \nonumber \]

\[\gamma \simeq i2\pi f\sqrt{\widetilde{L}\widetilde{C}}\times \left ( 1+\frac{1}{2}\frac{1}{i2\pi \pi f} \left ( \frac{\widetilde{G}}{\widetilde{C}} +\frac{\widetilde{R}}{\widetilde{L}}\right )\right ) \nonumber \]

\[\gamma \simeq i2\pi f\sqrt{\widetilde{L}\widetilde{C}}+\frac{1}{2} \left ( \widetilde{G}\sqrt{\frac{\widetilde{L}}{\widetilde{C}} }+\widetilde{R}\sqrt{\frac{\widetilde{C}}{\widetilde{L}}}\right ) \nonumber \]

Así, la constante de atenuación (espacio) es igual a la parte real de esta expresión, e igual

\[a(f)=\frac{\widetilde{G}Z_{0}+\frac{\widetilde{R}}{Z_{0}}}{2} \nonumber \]