19: Conclusión

1. Solucionador de Excel

Considere una empresa perfectamente competitiva (PC) con una función de costo total dada por\(TC=100q^{\frac{1}{2}} \). Dividir ambos lados por q nos da la función de costo promedio,\(ATC=100q^{-\frac{1}{2}} \). Tomando la derivada de TC con respecto a q rendimientos\(MC=50q^{-\frac{1}{2}}\).

Si esta firma de PC enfrentaba un precio de mercado de $5 por unidad, ¿cuál es el nivel de producción maximizador de ganancias?

Este libro ha resuelto problemas de optimización a través de métodos numéricos y analíticos. Aplicaremos ambos métodos a este problema. Primero, usaremos Solver.

Pero no vamos a utilizar un libro de Excel preparado. En cambio, crearás tu propia implementación de este problema. Hay, por supuesto, pasos útiles para guiarte.

PASO Abra un libro de Excel en blanco. En la celda A1, escriba la palabra cantidad. La celda B1 contendrá un número que representa la cantidad. En la celda A2, escriba la palabra ganancias. En la celda B2, ingrese la fórmula para obtener ganancias.

El precio es de $5 por unidad y\(TC=100q\) así la fórmula en la celda B2 es: =5*B1−100*SQRT (B1).

PASO Ejecutar Solver. La celda objetivo es B2, el objetivo es obviamente maximizar las ganancias, y la celda cambiante es B1. No hay restricciones porque la firma de PC es libre de producir toda la producción que quiera al precio dado

Excel da un resultado miserable. Dependiendo de tus valores predeterminados de Solver, podría ir negativo y, como Excel no puede tomar la raíz cuadrada de un número negativo, se da por vencido y anuncia su fracaso.

Si es así, haga que A1 sea cero y vuelva a ejecutar Solver, pero esta vez, marque la opción Hacer variables no restringidas no negativas. Su Solver puede estar configurado de modo que la opción Crear variables no restringidas no negativas ya estaba marcada, por lo que es posible que no vea el primer resultado miserable.

A partir de cero (o una celda en blanco) en A1, con la restricción de no negatividad, Solver dice que la respuesta es cero. Esto es preocupante. ¿Podría ser realmente cero la cantidad óptima?

A lo mejor el tema es que estamos partiendo de celda en blanco, que es cero. Esto es una mala práctica. Excel interpreta los espacios en blanco como un cero y la fórmula en B1 se evalúa a cero. Tratar los espacios en blanco como cero es una de las cosas más peligrosas que hace una hoja de cálculo (las hojas de Google se comportan de la misma manera). Siempre debes evitar esto.

Podemos cambiar de donde parte Solver para ver si eso ayuda.

PASO Cambiar la celda B1 a 25. La celda B2 debe mostrar −375. Ejecute Solver.

Solver parece convencido de que la solución óptima es cero. Pasamos a los métodos analíticos para ver si podemos confirmar el resultado de Solver.

Sabemos\(MC=50q^{-\frac{1}{2}}\) y como es una firma de PC MR = P entonces MR = 5. Podemos establecer MR = MC y resolver para q óptima. \[5=50q^{-\frac{1}{2}} \rightarrow q^{\frac{1}{2}} = 10 \rightarrow q* = 100 \nonumber \]

Esto es confuso. Ahora tenemos dos respuestas: q = 0 y q = 100. ¿Cuál es la correcta?

A lo mejor una gráfica ayudará. Podemos dibujar la gráfica canónica del problema de maximización de ganancias de producción de la empresa. La Figura IV.1 muestra las curvas de costo y podemos ver claramente que MR = MC produce un rectángulo de beneficio negativo.

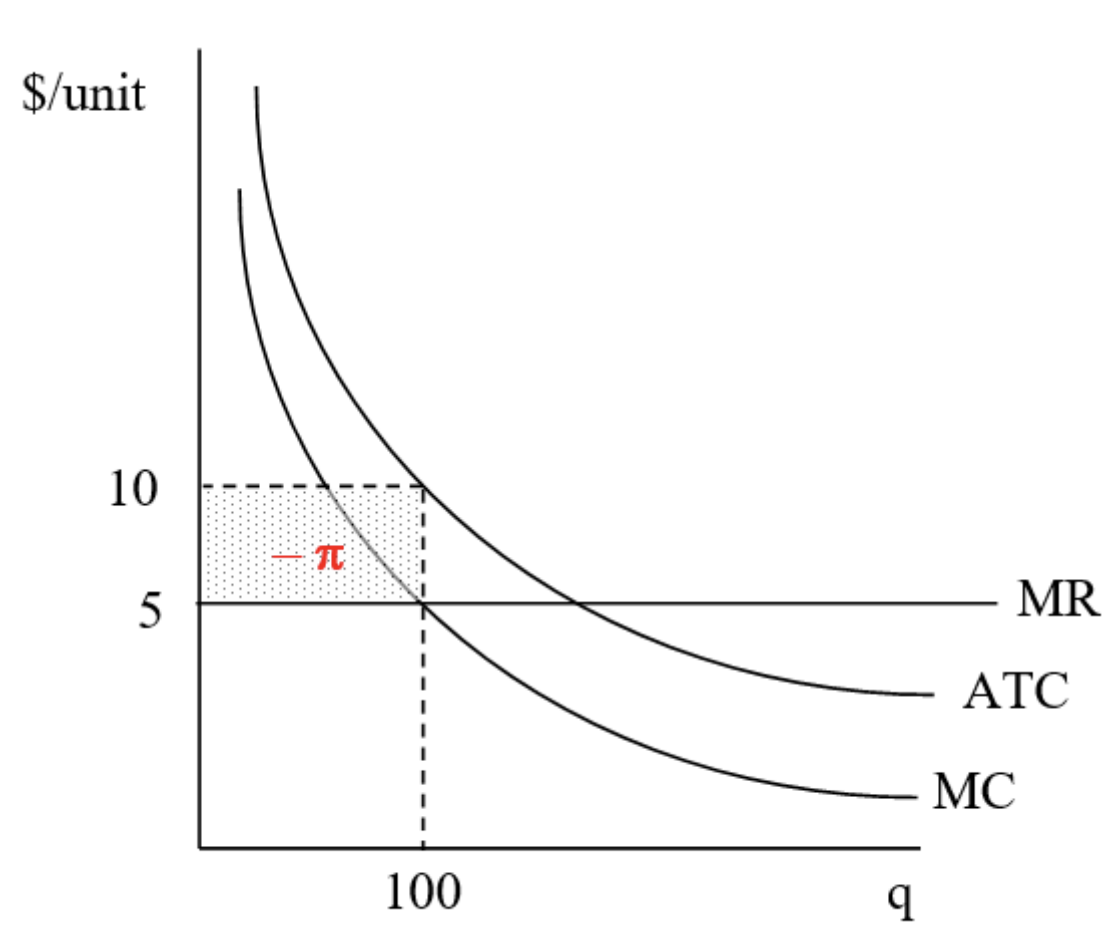
Esta gráfica ayuda a explicar lo que está pasando aquí, pero necesitamos una mejor visual. Este libro afirmaba que mirar directamente a la función de ganancias dejó en claro la Regla de Cierre así que intentemos ese enfoque.

PASO Crea una columna de 0 a 500 por 10. Esta es la cantidad. Utilice la fórmula de ganancias para crear una columna de ganancia basada en la cantidad. Crea una gráfica de las dos columnas.

Si te atascas, este video de 2 minutos en vimeo.com/425873093 muestra cómo hacerlo.

En la Figura IV.2 se muestra la gráfica realizada en el video. Se deja claro que el punto donde MR = MC es en realidad un punto de beneficio mínimo. Aunque se cumple la condición de primer orden (encontramos un punto plano en la función de ganancia en q = 100), esta solución falla la condición de segundo orden para un máximo.

Así, la respuesta correcta es producir una infinidad de salida. Las ganancias suben a medida que se producen más allá de las 100 unidades de producción. Un mayor rendimiento que conduce a mayores ganancias continúa para siempre, por lo que la solución óptima es infinito.

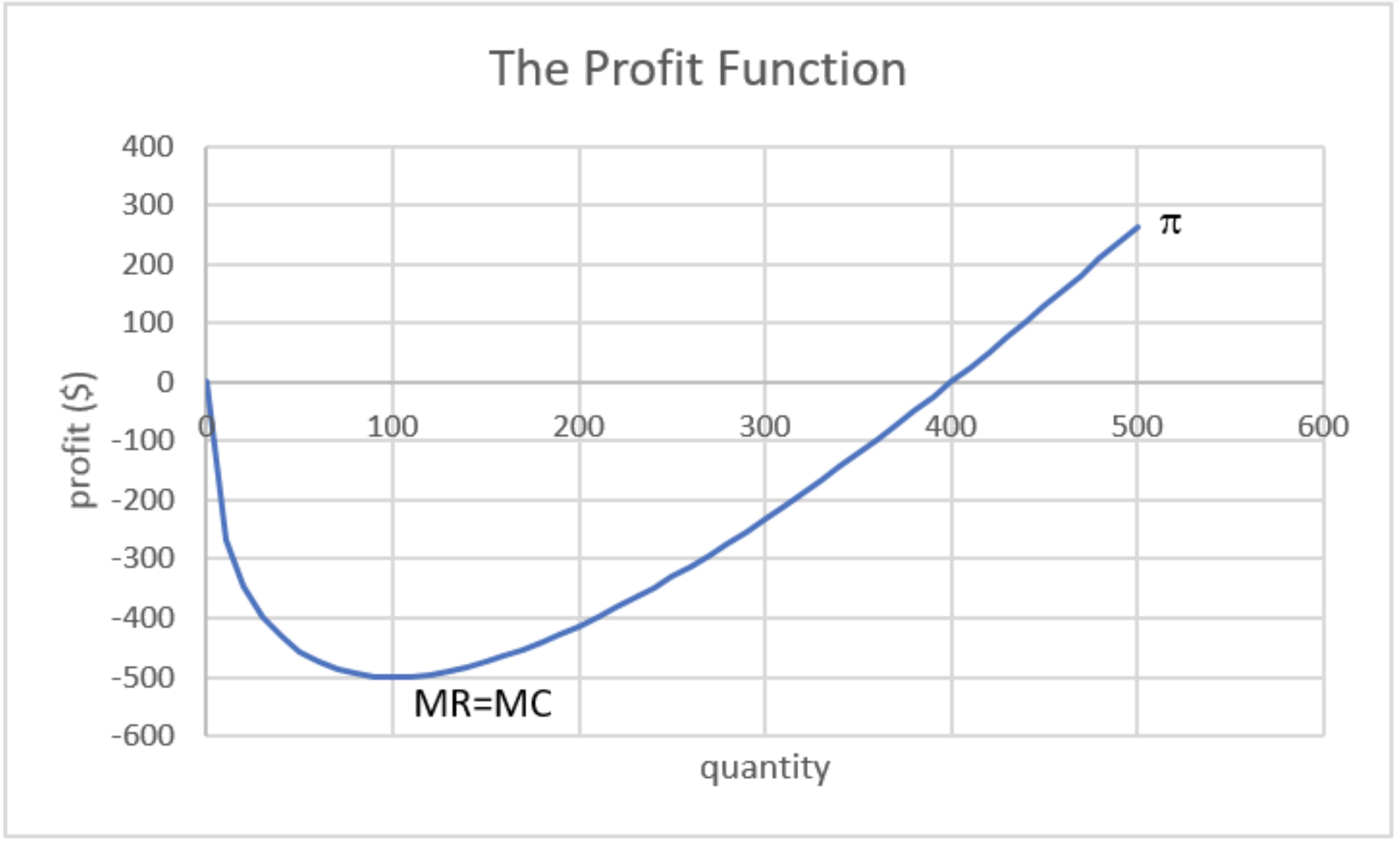
¿Cómo podemos explicar la respuesta de Solver de cero? ¿Por qué no nos da la respuesta correcta? Cuando Solver inicia desde abajo de 100 (empezamos desde cero y 25), pasa a cero (o salida negativa si no se tiene una restricción de no negatividad). ¿Qué pasa si parte de un número mayor a 100?

PASO Ingresa 110 en la celda A1 y ejecuta Solver.

Solver reporta que “Las celdas objetivas no convergen”. ¿Es este un resultado miserable? No, en realidad, ¡es la respuesta correcta! Cuando Solver inicia desde más de 100, va justo en el\(x\) eje y las ganancias suben y sigue y va. Como sabemos, esta es la respuesta correcta.

Vale la pena recordar que el algoritmo de Solver es ingenuo. Evalúa la función en el valor inicial, luego se mueve hacia la izquierda y hacia la derecha. El tamaño del movimiento depende de los valores numéricos en el problema. A partir de q = 25, por ejemplo, Solver se mueve un poco a la derecha, ve que las ganancias cayeron, luego va en sentido contrario y baja la producción. Puede ver los pasos del Solver marcando la opción Mostrar resultados de iteración después de hacer clic en el botón Opciones en el cuadro de diálogo Solver.

Podrías estar pensando que como estamos a la larga, ATC = AVC y es claro que P < AVC en MR = MC, lo que significa que la firma debería cerrar. Eso no es malo pensar, salvo que la regla no funciona en MR = MC en este caso porque esa no es la salida maximizadora de ganancias.

La conclusión de este último ejemplo es que tienes que saber lo que estás haciendo con Solver. No es perfecto y no se puede confiar ciegamente en sus resultados. Este ejemplo muestra que los métodos numéricos se van a utilizar con precaución. Ten cuidado ahí fuera.

2. Vista general

Este libro cubrió la teoría microeconómica ortodoxa moderna a nivel universitario. Utilizó Excel para presentar material difícil y mostró cómo las matemáticas pueden ser utilizadas para resolver problemas en economía.

El enfoque económico o la forma económica de pensar proporcionó el marco para analizar el comportamiento observado. La idea básica es configurar y resolver un problema de optimización o modelo de equilibrio. A continuación, se cambia una sola variable, ceteris paribus, y la nueva solución se compara con la solución inicial. Este procedimiento se denomina estática comparativa. La elasticidad captura la lógica de la estática comparativa en un solo número.

Cuando el enfoque económico se aplica a los consumidores, se llama Teoría del Comportamiento del Consumidor. El análisis estadístico comparativo clave es derivar la curva de demanda. La Figura IV.3 es una gráfica canónica de la demanda derivada.

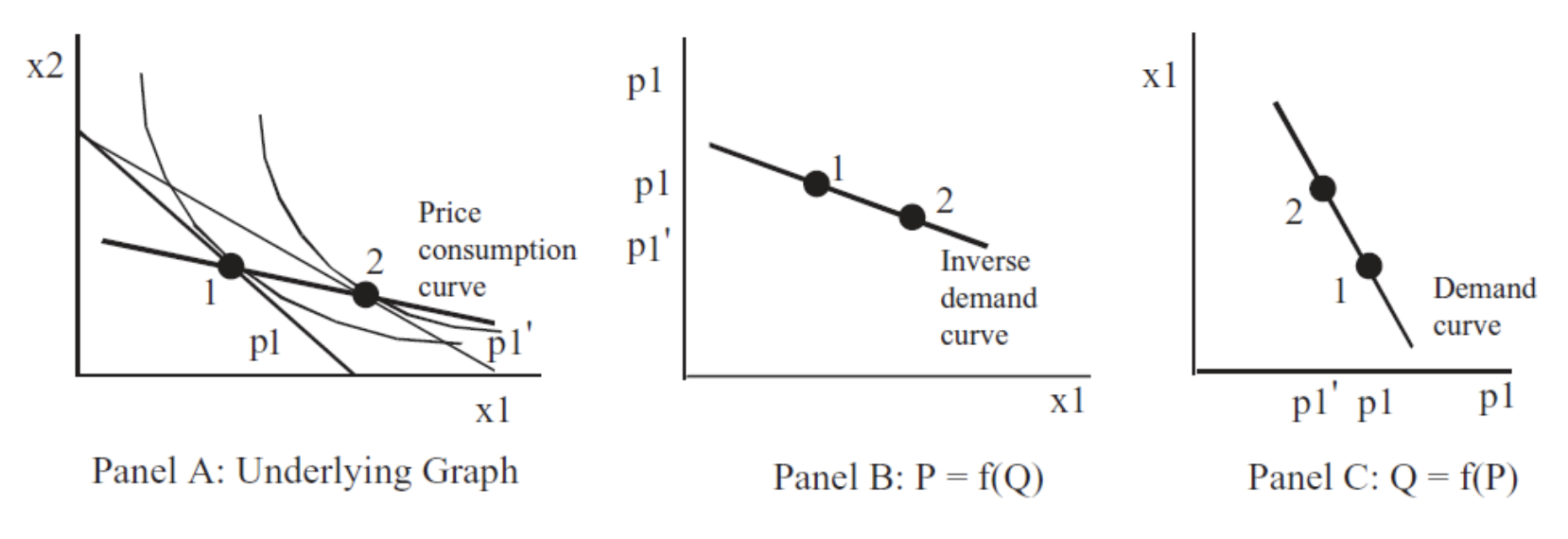
Cuando el enfoque económico se aplica a los productores, se denomina Teoría de la Firma. El análisis estadístico comparativo clave es derivar la curva de oferta. La Figura IV.4 es una gráfica canónica del suministro derivado.

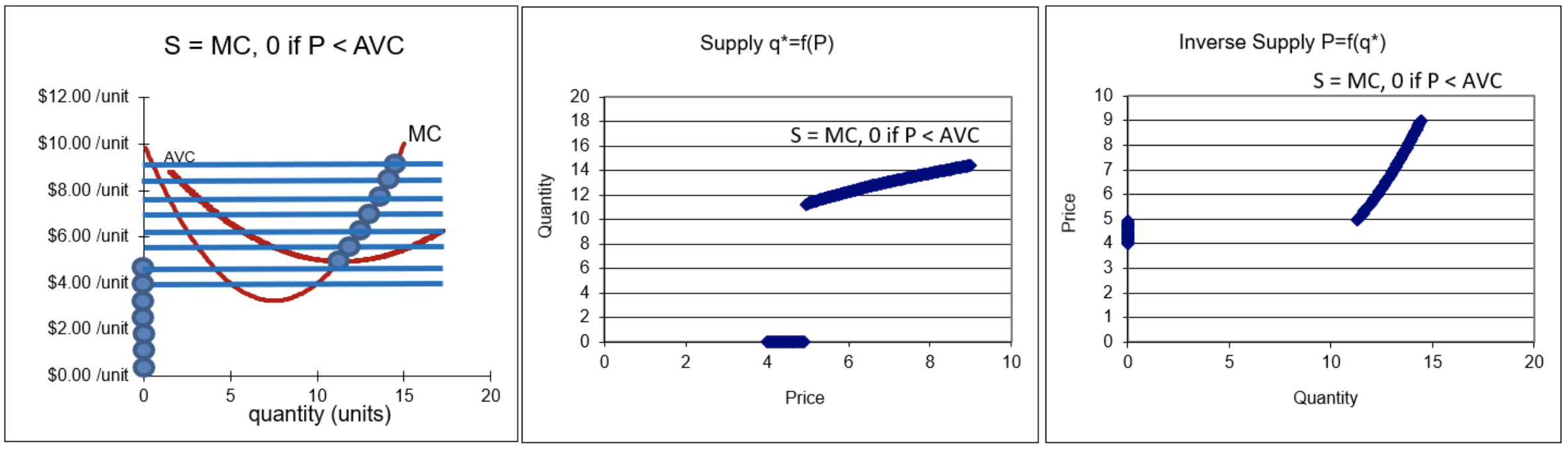
La firma es más complicada que el consumidor porque las firmas contratan insumos para producir producción. De hecho, la empresa es realmente un conjunto de tres problemas de optimización interrelacionados: minimización de costos de entrada, maximización de ganancias de salida y maximización de ganancias de entrada.

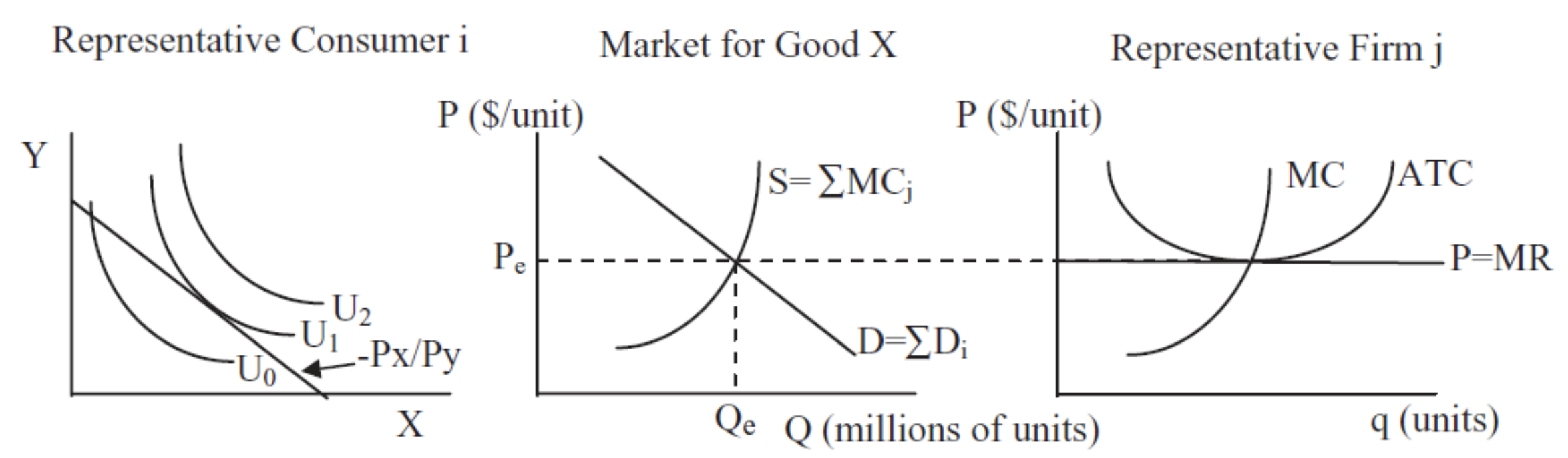
Las curvas individuales de demanda y oferta derivadas de los modelos de consumidor y empresa se pueden sumar para producir curvas de demanda y oferta del mercado. Esto permite un análisis de equilibrio parcial de cómo los mercados resuelven la cuestión de asignación de recursos de la sociedad. La figura IV.5 muestra la oferta y la demanda flanqueadas por sus gráficas de fuente de consumo y firma.

Los techos de precios, impuestos, monopolio, cuotas de importación y externalidades son ejemplos de situaciones en las que tenemos una mala asignación de recursos en un mercado único.

El equilibrio parcial permite calcular una medida de ineficiencia llamada pérdida de peso muerto (también conocida como el triángulo de Harberger), pero esto debe interpretarse como una aproximación porque el excedente de los consumidores requiere que se haga un ajuste a la curva de demanda ordinaria (se debe usar demanda compensada) y se ignoran los efectos en otros mercados. El análisis de equilibrio parcial se utiliza comúnmente en el trabajo empírico. Piense en la pérdida de peso muerto como una medida aproximada de ineficiencia en la asignación de recursos.

El equilibrio general es un análisis más riguroso y sofisticado porque mira a todos los mercados como un sistema total. Los criterios de Pareto muestran que un mercado que funcione correctamente produce una asignación óptima y el monopolio no es Pareto óptimo. La Figura IV.6 es la gráfica canónica del equilibrio general de un mercado y deja claro que la asignación del mercado no tiene puntos Pareto Superior.

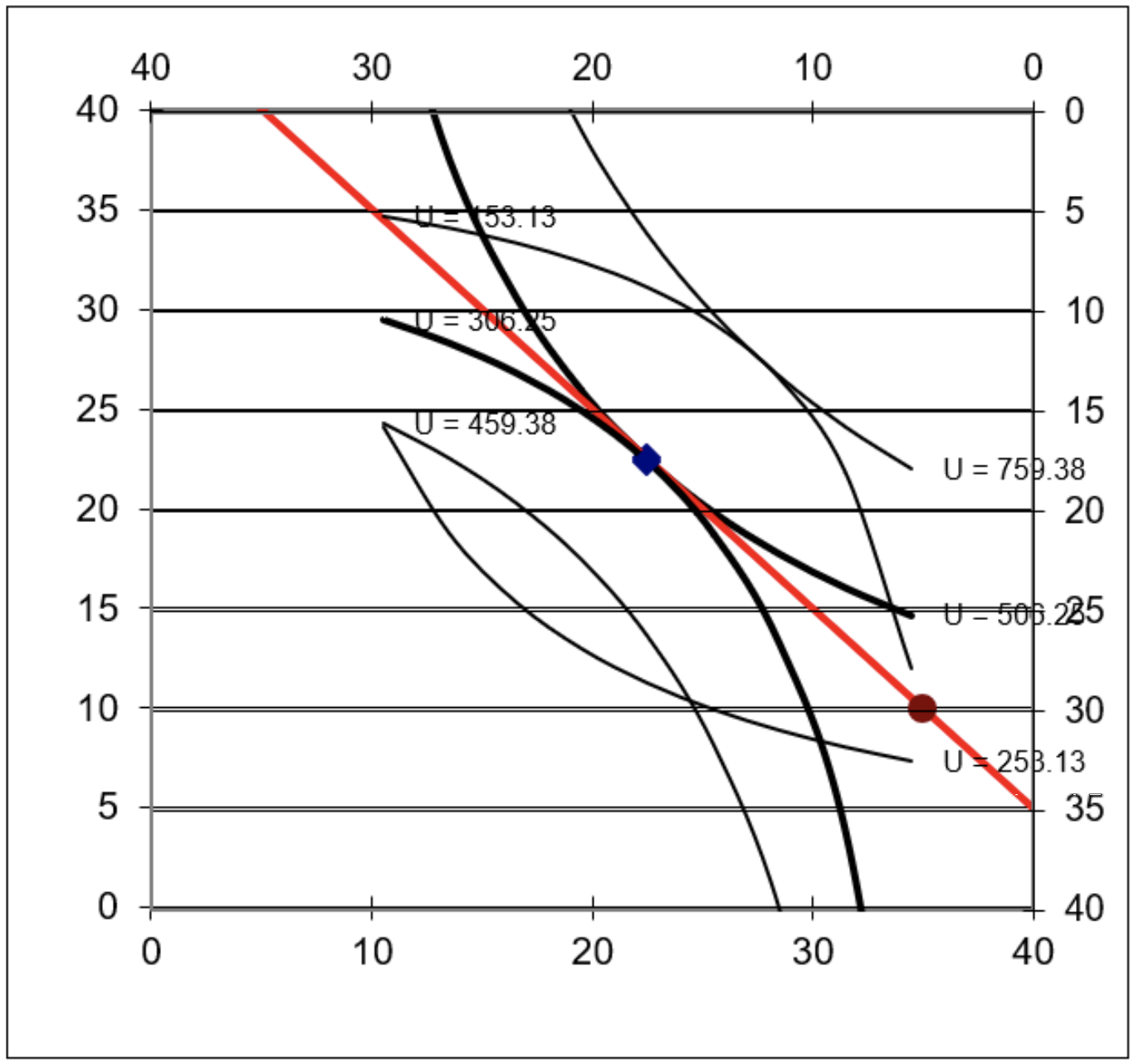
El equilibrio general no sufre los mismos problemas que el equilibrio parcial, pero es mucho más difícil de implementar en el mundo real. En el epígrafe de la sección de introducción de la Caja Edgeworth, se mencionaron modelos de equilibrio general computables. Esto demuestra que existe un lado empírico en el análisis de equilibrio general, pero es un desarrollo relativamente moderno.

Es razonable considerar la microeconomía convencional como una teoría del mecanismo de precios. El sistema de mercado utiliza los precios como señales para asignar recursos. Los agentes optimizadores reaccionan a los cambios de precios y sus interacciones a medida que compradores y vendedores impulsan el sistema hacia el equilibrio Las Teorías del Comportamiento del Consumidor y la Firma son peldaños que explican cómo el mercado responde a la pregunta de asignación de recursos de la sociedad. La Figura IV.5 une la Teoría del Comportamiento del Consumidor, la Teoría de la Firma y el análisis de equilibrio parcial. Vale la pena recordar estas tres gráficas y cómo encajan entre sí.

Otra organización de la microeconomía la divide en dos partes: agentes individuales (consumidores y empresas) que optimizan y qué sucede cuando estos agentes optimizadores interactúan en un mercado. El primero se trata de optimización y el segundo se trata de equilibrio. El orden que se genera espontáneamente al interactuar, optimizar los agentes es un resultado notable. Los economistas ven la oferta y la demanda no como la simple intersección de dos líneas, sino como un patrón que sin saberlo es generado por los propios agentes, al igual que los gansos que vuelan en una V.

Este libro fue diseñado para brindarle práctica en la aplicación del enfoque económico. Abordamos problemas de optimización no restringidos y restringidos, calculamos muchas elasticidades diferentes y resolvimos varios modelos de equilibrio a nivel parcial y general.

Las múltiples aplicaciones del enfoque económico demuestran su notable flexibilidad. La Teoría del Comportamiento del Consumidor, al principio, parece ridículamente irrealista: ¡un consumidor robot elige entre dos bienes con precios, gustos e ingresos dados! Pero ese es sólo el modelo básico. Al cambiar los bienes a consumo en el presente y en el futuro, se convierte en un modelo de elección intertemporal. Analizamos la donación caritativa, la teoría de la cartera y el efecto de las características de seguridad en automóviles con la Teoría del Comportamiento del Consumidor.

En cada aplicación, la forma económica de pensar era prominente. Configuramos y resolvimos un problema de optimización, luego cambiamos una variable, ceteris paribus, para ver cómo cambió la solución óptima. Existen innumerables aplicaciones del enfoque económico, pero comparten el mismo marco y lógica.

De hecho, el enfoque económico es lo que define la economía actual. Puede ser la única disciplina que se define por una metodología en lugar de por lo que estudia. La mayoría de las personas tienen una definición de economía basada en el contenido: Piensan que el estudio de las tasas de interés, el desempleo y el dinero es economía. Pero esto está mal. La definición adecuada de economía es la aplicación del enfoque económico para explicar el comportamiento observado. El crimen, el matrimonio y la guerra, si se analizan con el enfoque económico, caen bajo el rubro de economía.

A partir de ahora, cuando escuches la frase “un análisis económico de”, sabrás que el enfoque económico está por aplicarse, sabrás qué esperar, y estarás cómodo mientras el orador habla de limitaciones, optimalidad, estática comparada y elasticidad.

3. Un problema abierto

Ni este libro ni la economía moderna y convencional explican el proceso dinámico del capitalismo. Unos cientos de años del sistema de mercado hacen evidente que la creatividad, la innovación y el cambio tecnológico son generados endógenamente por sociedades basadas en el mercado. Nadie sabe realmente por qué.

La pregunta ha sido con la economía desde el principio. Mucha gente sabe que Adam Smith escribió un libro llamado La riqueza de las naciones, pero sólo unos pocos saben que el título real es, Una investigación sobre la naturaleza de las causas de la riqueza de las naciones. Pero ¿cuál fue la indagación de Smith, en pocas palabras?

Quería saber por qué Inglaterra era tanto más rica que sus vecinos. En 1776, Smith pudo ver la riqueza británica a su alrededor. Podía ver despegar la economía y se preguntó por qué algunos lugares se desarrollan y crecen, mientras que otros parecen no poder hacerlo. Esta pregunta sigue sin respuesta y, en el lenguaje de las matemáticas, es el mayor problema abierto de la economía.

Explicar el dinamismo del sistema de mercado es una cuestión muy diferente a la de los modelos de optimización estática y equilibrio que explican por qué los mercados asignan recursos de manera eficiente. En el mundo estático, no hay nuevos productos, innovaciones que ahorren costos o nuevas firmas. El mundo estático es estable y los mercados están en equilibrio.

Este modelo estático choca violentamente con la realidad. La interpretación de Joseph Schumpeter de lo que llamó capitalismo plausible (es decir, del mundo real), capturado en el oxímoron “destrucción creativa”, destaca el ascenso y la caída de las empresas, el crecimiento explosivo y la dislocación producida por los mercados. Para Schumpeter, la fuerza impulsora es el emprendedor, un héroe cuyo deseo de dominar el mundo empresarial da como resultado el éxito económico para la sociedad. Pero la historia de Schumpeter (mejor capturada en Capitalismo, Socialismo y Democracia, publicada originalmente en 1942), aunque emocionante sea, no forma parte de la economía convencional hoy en día.

Es claro que los mercados sí generan un crecimiento económico espectacular, sin igual por cualquier otra forma organizativa. Incluso los críticos más duros del capitalismo reconocen este punto:

La burguesía, durante su reinado de escasos cien años, ha creado fuerzas productivas más masivas y colosales que todas las generaciones precedentes juntas. Sujeción de las fuerzas de la naturaleza al hombre, maquinaria, aplicación de la química a la industria y la agricultura, navegación a vapor, ferrocarriles, telégrafos eléctricos, limpieza de continentes enteros para cultivo, canalización de ríos, poblaciones enteras expulsadas del suelo, lo que antes de siglo tenía incluso un presentimiento que esas fuerzas productivas dormían en el regazo del trabajo social?

Eso fue escrito por Karl Marx y Friedrich Engels en El Manifiesto Comunista en 1848, disponible en www.marxists.org/archive/marx/works/download /pdf/Manifesto.pdf.

Marx y Engels argumentaron que el capitalismo se autodestruirá, pero no porque no logró fabricar bienes y servicios. Pensaron que era el sistema más productivo jamás ideado. Quedaron asombrados por la capacidad del capitalismo para generar producción.

Marx y Engels no fueron los primeros ni los últimos en quedar asombrados por el poder productivo del sistema de mercado. Sin embargo, aunque podamos ver fácilmente ese poder productivo, simplemente no conocemos la respuesta a preguntas básicas sobre cómo los mercados generan crecimiento. Más allá de generalidades superficiales sobre el entorno institucional, como la necesidad de Estado de Derecho y derechos de propiedad establecidos, no tenemos explicación de cómo la interacción de multitudes de agentes impulsa el sistema a lo largo del tiempo. Ni siquiera podemos responder a la pregunta más básica, planteada por Adam Smith: ¿por qué algunos países son ricos y otros pobres?

Si supiéramos cómo y por qué los mercados provocaron que el cambio tecnológico y la producción por persona crecieran exponencialmente, sabríamos cómo ayudar a aquellas sociedades sumidas en la pobreza. El economista ganador del Premio Nobel Robert Lucas plantea el tema de esta manera:

¿Hay alguna acción que pueda tomar un gobierno de la India que conduzca a que la economía de la India crezca como la de Indonesia o Egipto? Si es así, ¿qué, exactamente? Si no, ¿qué tiene 'la naturaleza de la India' lo que la hace así? Las consecuencias para el bienestar humano involucradas en preguntas como estas son simplemente asombrosas: Una vez que uno empieza a pensar en ellas, es difícil pensar en otra cosa. (Lucas, 1988, p. 5)

El punto es el siguiente: Los mercados pueden analizarse desde perspectivas estáticas y dinámicas. El primero se enfoca en la asignación de recursos en un solo momento en el tiempo. Congela la película y pregunta cómo funcionan los mercados en este ambiente inmóvil. Sabemos cómo funcionan los mercados como mecanismo de asignación de recursos.

Esta última perspectiva es sobre la naturaleza dinámica de los mercados, queremos saber cómo funcionan los mercados a lo largo del tiempo. Las corridas de la película: los brotes de rápido crecimiento van seguidos de recesiones, luego más crecimiento, pero la producción por persona tiende al alza. ¿Esto continuará? No lo sabemos. ¿Cómo surgen las instituciones en las que confiamos (incluidos los derechos de propiedad) de la interacción de los agentes optimizadores? No lo sabemos.

Explicar los mercados como un proceso dinámico sigue siendo el problema abierto más importante en la economía. Quizás puedas trabajar en ello.

Referencias

El epígrafe es de las páginas 14 y 15 de Lionel Robbins, An Essay on the Nature and Significance of Economic Science (publicado originalmente en 1932) y disponible en línea en mises.org/biblioteca/ensayo-naturaleza-y-significancia-economicscience.

Comenzamos con una famosa cita de Robbins, definiendo la economía como “la ciencia que estudia el comportamiento humano como una relación entre fines dados y medios escasos que tienen usos alternativos”. Este libro toma en serio esta definición y ha enfatizado la optimización estática, pero este último capítulo deja claro que tenemos mucho por descubrir y aprender sobre dinámicas y avances tecnológicos.

Robert Lucas, “Sobre la mecánica del desarrollo económico”, Journal of Monetary Economics, Vol. 22 (1988), pp. 3—42, www.sciencedirect.com/sci ence/article/abs/pii/0304393288901687.

El hecho de que la competencia perfecta sea incompatible con rendimientos crecientes (como\(TC=100q^{\frac{1}{2}}\) mostró el ejemplo de Solver con) llevó a un acalorado debate en la década de 1920. La economía sigue luchando para desarrollar un modelo que combine el hecho de que el costo promedio cae a medida que aumenta la producción para muchos productos con mercados competitivos. Véase David Warsh (2006), El conocimiento y la riqueza de las naciones: una historia de descubrimiento económico, para una revisión de cómo la economía ha lidiado con el tema del aumento de los rendimientos.

Si te interesa la trayectoria del capitalismo y los mercados, entonces la teoría económica moderna no será de mucha ayuda. Para una entretenida reseña del capitalismo y cómo se le ha tratado en economía, nadie ha vencido a este clásico: Robert Heilbroner, The Wordly Philosophers: The Lives, Times e Ideas of the Great Economic Thinkers (Nueva York: Touchstone, 1999, 7a edición, publicada originalmente 1953).