Al igual que la firma perfectamente competitiva, un monopolista tiene tres problemas de optimización interrelacionados. La atención se centra en el problema máximo de ganancia de salida porque ahí es donde radica la diferencia esencial entre una empresa perfectamente competitiva (PC) y un monopolio. Sabemos que a través de la consistencia, el poder de monopolio se manifiesta también en el lado de entrada. Un monopolio producirá menos que una firma de PC y, a su vez, contratará menos mano de obra y capital.
A diferencia de una firma de PC, un monopolio elige la salida y el precio al que vender el producto. Esto hace que el problema del monopolio sea más difícil de resolver. Afortunadamente, su experiencia con la optimización, la estática comparativa y las pantallas gráficas le brindan los antecedentes necesarios para comprender y dominar el monopolio.
Definición y problemas
Un monopolio se define como una firma que es el único vendedor de un producto sin sustitutos cercanos. La definición es inherentemente vaga porque no hay una demarcación clara para lo que constituye un sustituto cercano.
Considera este ejemplo: En los viejos tiempos, un proveedor de cable local podría tener un acuerdo exclusivo para proporcionar televisión por cable en una comunidad. Se podría argumentar que el proveedor de cable era un monopolio porque era el único vendedor de televisión por cable. Pero, ¿cuáles son los sustitutos de la televisión por cable?
Hace años, la televisión por cable era la única forma de acceder a canales de suscripción como ESPN y HBO. Las transmisiones comerciales (con emisoras nacionales como ABC, NBC y CBS y canales locales) fueron un mal sustituto de la televisión por cable. En este entorno, la televisión por cable sería un buen ejemplo de monopolio.
Hoy, sin embargo, la televisión por cable tiene una fuerte competencia de los servicios satelitales y los servicios de transmisión desde la web. Aunque una firma tuviera una franquicia exclusiva para entregar televisión por cable en una comunidad, hay muchas maneras de obtener esencialmente el mismo paquete de canales. Hoy en día, la televisión por cable no es un monopolio.
Por supuesto, la televisión por cable tampoco es un buen ejemplo de competencia perfecta. La compañía de cable no acepta el precio como una variable dada. Está en el medio, en algún lugar entre la competencia perfecta y el monopolio. Los mercados atendidos por algunas firmas se llaman oligopolios. Agrega más firmas y eventualmente obtienes competencia monopolística. El estudio de cómo se comportan las empresas bajo una variedad de estructuras de mercado forma parte de la subdisciplina de la economía llamada Organización Industrial. La figura 15.1 resume las cosas.
Figura 15.1: Un continuo de estructuras de mercado.
Barrera a la entrada
Para seguir siendo un monopolio, la firma debe tener una barrera de entrada para impedir que otras firmas vendan su producto. En el ejemplo de televisión por cable, la barrera de entrada fue proporcionada por el acuerdo exclusivo con la comunidad. Dicha restricción gubernamental es una forma común de barrera de entrada.
Otra forma de erigir una barrera de entrada es controlar una entrada necesaria. ALCOA (la Aluminum Corporation of America) tenía el monopolio del aluminio a principios del siglo XX porque poseía prácticamente todas las reservas de bauxita.
Si un producto requiere entrada a gran escala, como la fabricación de automóviles, esto se considera una barrera de entrada. Para competir contra compañías automotrices establecidas, una firma no solo debe producir automóviles, sino también muchas piezas de repuesto y averiguar cómo vender el producto.
Al igual que el concepto de un sustituto cercano, una barrera de entrada no es un simple problema de sí o no. Las barreras pueden ser débiles o fuertes y pueden cambiar con el tiempo. La barrera de la televisión por cable se vio erosionada no por los cambios en las normas legales, sino por el cambio tecnológico, la llegada de la televisión vía satélite y la web.
Función de ingresos de Monopoly
Sabemos que la estructura de mercado de la firma impacta su función de ingresos. El caso más simple es una firma perfectamente (o puramente) competitiva. Toma precio según lo dado y, por lo tanto, los ingresos son simplemente precio veces cantidad. Para un competidor perfecto, aunque la demanda del mercado es descendente, la curva de demanda individual de la firma es perfectamente elástica al precio de mercado dado.
Debido a que la firma de PC puede vender todo lo que quiera al precio dado, vender una unidad más de producción hace que los ingresos totales (TR) aumenten por el precio del producto. Los ingresos marginales (MR) se definen como el cambio en TR cuando se vende una unidad más. Así, para una firma de PC,\(MR = P\).
Esto no es cierto para un monopolio. Una implicación crítica del poder monopolista es que la RM diverge de la curva de demanda. Pero esto es demasiado abstracto. Podemos usar Excel para aclarar estos conceptos.
PASO Abra el libro de Excel Monopoly.xls y lea la hoja de introducción, luego vaya a la Hoja de ingresos para ver cómo el poder de monopolio afecta la función de ingresos de la empresa.
La hoja se abre con una estructura de ingresos perfectamente competitiva. El ingreso total es una función lineal de la salida y, por lo tanto,\(P = MR\) con una línea horizontal en la gráfica inferior. Una gráfica con TR lineal y MR horizontal correspondiente significa que es una firma de PC.
A diferencia de una firma de PC, un monopolio enfrenta la curva de demanda descendente del mercado. Podemos modelar una curva lineal de demanda inversa simplemente como\(P = p_0 - p_1q\). Debido a que el parámetro de pendiente\(p_1\), en la celda T2 es inicialmente cero, TR es lineal y MR es horizontal.
PASO Para mostrar cómo el poder de monopolio afecta la función de ingresos de la empresa, haga clic en la barra de desplazamiento de Pendiente de precios.
Observe que a medida que aumenta el parámetro de pendiente, MR diverge más de D.
Cuanto menor (en valor absoluto) es la elasticidad de precio de la demanda, mayor es la divergencia de la RM de D y más fuerte es el poder de monopolio.
Veremos que el monopolista utiliza la divergencia de MR de D para extraer mayores ganancias de las que serían posibles si hubiera otros vendedores del producto.
Al dibujar MR y D en el caso de una curva lineal de demanda inversa, tenga en cuenta estas dos reglas básicas:
MR y D tienen la misma intercepción.
MR bisecta el eje y y D.
Podemos derivar estas propiedades fácilmente. Con nuestra curva D inversa,\(P = p_0 - p_1q\), podemos hacer lo siguiente:\[TR=Pq\]\[TR = (p_0 - p_1)q\]\[TR = p_0q - p_1q\]\[MR = \frac{dTR}{dq} = p_0 - 2p_1\] Claramente, tanto D como MR comparten la misma intercepción,\(p_0\). Debido a que la pendiente de MR es\(-2p_1\), es el doble de la pendiente de D, que es simplemente\(-p_1\).
Así, cuando dibujas una curva lineal de demanda inversa y luego te preparas para dibujar la curva MR correspondiente, recuerda las dos reglas: (1) la intersección es la misma y (2) MR tiene el doble de pendiente así que en cada valor del eje y, MR está a medio camino entre la y eje y la curva D.
La Figura 15.2, con una pendiente de curva de demanda inversa de\(-1\), muestra la función de ingresos del monopolio. A diferencia de la firma de PC, TR es una curva y MR diverge de D.MR bisecta el eje y y D. La línea discontinua a $20/unidad, por ejemplo, muestra que la distancia desde el eje y hasta MR es de 10, lo mismo que MR a D.
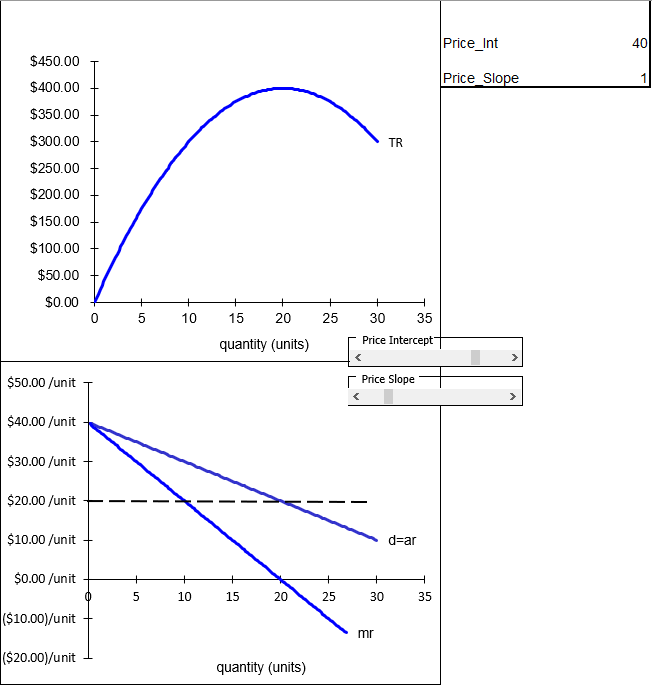
Figura 15.2: Funciones TR, D y RM para un monopolista.
Fuente: Monopoly.xls! Ingresos
Observe que donde MR = 0 a q = 20, TR está en su máximo. A esta cantidad, la elasticidad de precio de la demanda es exactamente\(-1\).
La Figura 15.2 muestra que la RM puede ser negativa. Esto puede suceder porque hay dos fuerzas opuestas en el trabajo. Al aumentar la cantidad aumenta TR, ya que\(TR= Pq\). Sin embargo, la única manera de vender ese producto extra es bajar el precio (viajando por la curva de demanda) por lo que TR cae. Cuando el incremento a TR por venta de salida adicional supera el efecto de la caída en el precio, MR es positivo. Eventualmente, sin embargo, con una curva lineal de demanda, el monopolista llegará a un punto en el que el incremento en los ingresos por vender una unidad más es negativo. En el rango de producción (\(q > 20\)en la Figura 15.2) donde\(MR < 0\), el efecto de la disminución del precio supera al efecto positivo de vender más producción.
Cuando\(MR > 0\), la elasticidad de precio de la demanda es mayor a 1 (en valor absoluto). Cuando la RM es negativa, la demanda es inelástica. El monopolista nunca producirá en la parte negativa de MR, que es lo mismo que la porción inelástica de la curva de demanda.
Existe una fórmula ordenada que expresa la relación entre MR y P. Con una curva de demanda inversa\(P(Q)\),, lo sabemos\(TR = P(Q)Q\). De la función TR podemos tomar la derivada con respecto a la salida para encontrar la función MR. Usamos la Regla del Producto:\[MR=\frac{dTR}{dQ}=P+\frac{dP}{dQ}Q\] Si factorizamos P a partir de esta expresión, entonces MR se puede reescribir como:\[MR=P+\frac{dP}{dQ}Q=P(1+\frac{dP}{dQ}\frac{Q}{P})=P(1+\frac{1}{\epsilon})\] La letra griega épsilon (\(\epsilon\)) es la elasticidad de precio de la demanda (\(\frac{dQ}{dP}\frac{P}{Q}\)). La expresión muestra que\(MR = P\) bajo competencia perfecta porque una firma individual se enfrenta a una curva de demanda perfectamente elástica. Esto significa épsilon es infinito y su recíproco es cero.
También muestra que cuanto más inelástica es la curva de demanda (cuanto más cerca\(\epsilon\) está de 0), mayor es la separación entre MR y la curva de demanda (P). Si\(\epsilon = 0\), entonces MR es indefinido. Con\(\epsilon = 0\), la demanda inversa es una línea vertical. El monopolio cobraría un precio infinito.
Configuración del problema
Hay tres partes en cada problema de optimización. Aquí está el marco para el problema de maximización de ganancias del lado de la producción de un monopolista.
Objetivo: maximizar las ganancias (\(\pi\)), que equivalen a los ingresos totales (TR) menos los costos totales (TC).
Variables endógenas: salida (q) y precio (P)
Variables exógenas: precios de entrada (tasa salarial y tasa de renta de capital), coeficientes de función de demanda y tecnología (parámetros en la función de producción).
Un monopolio difiere de una firma de PC solo en el lado de ingresos el precio ahora es endógeno. La estructura de costos es la misma. El monopolio tiene un problema mínimo de costo de entrada y se utiliza para derivar una función de costo. Los aumentos en los precios de los insumos cambian las curvas de costos hacia arriba y las mejoras en la tecnología cambian las curvas El monopolista tiene un largo y corto plazo, al igual que una firma de PC, y a corto plazo hay una brecha entre ATC y AVC que representa costos fijos.
Encontrar la solución inicial
Primero mostraremos el enfoque convencional para resolver el problema del monopolio, luego recurriremos a una formulación alternativa basada en la optimización restringida.
El enfoque convencional es encontrar q óptimo donde\(MR=MC\), luego obtener P óptimo de la curva de demanda, y luego computar óptimo\(\pi\) como un rectángulo. Este es el enfoque estándar y hay una gráfica canónica que acompaña a este enfoque. Su principal virtud es que se puede comparar fácilmente con el caso perfectamente competitivo.
El enfoque convencional se puede demostrar con un problema concreto. Supongamos que la función de costo es\(TC = aq^3 + bq^2 + cq + d\). Supongamos que la curva de demanda del mercado (inversa) es\(P = p_0 - p_1q\). Así,\(TR=Pq=(p_0-p_1)q\).
Con esta información, podemos formar la función de ganancia y el problema de optimización de la firma, así:\[\begin{gathered} %star suppresses line # \max\limits_{q} \pi = TR-TC \\ \max\limits_{q} \pi = (p_0-p_1)q - (aq^3 + bq^2 + cq + d)\end{gathered}\]
Primero resolvemos este problema con métodos numéricos, luego analíticamente.
PASO Proceda a la hoja OptimalChoice y revísela.
La función de ganancia se ha ingresado en la celda B4. La cantidad y el precio se muestran como variables endógenas, pero q se pone en negrilla para indicar que es la variable endógena primaria. Es decir, Solver buscará la salida maximizadora de ganancias y, habiéndola encontrado, calculará el precio más alto que se pueda obtener de la curva de demanda.
La firma está obteniendo 245 dólares en ganancias al producir 10 unidades de salida y cobrando $34.50 por unidad, pero esta no es la solución maximizadora de ganancias. Esto lo sabemos porque el ingreso marginal de la 10ª unidad es de $29/unidad, mientras que el costo marginal de esa última unidad es de solo $4/unidad. Claramente, la firma debería producir más porque está ganando más ingresos adicionales de la última unidad producida que el costo adicional de producir esa unidad.
STEP Ejecute Solver para encontrar la solución óptima.
En la solución óptima, se cumple la condición equimarginal\(MR = MC\),,. Con ganancias positivas, esta es una señal clara de que hemos encontrado la respuesta.
Antes de hacer clic en el botón, intente hacer el problema por su cuenta. Esta es una maximización sin restricciones de una sola variable porque\(P = p_0 - p_1q\) ha sido sustituida en la función de ganancia. Tomar la derivada con respecto a q, ponerla igual a cero, y resolver para q óptima. Sustituir en los valores de los parámetros para convertirlo en un problema concreto facilita la matemática:\[\begin{gathered} %star suppresses line # \max\limits_{q} \pi = (40-0.55)q - (0.04q^3 - 0.9q^2 + 10q + 50)\end{gathered}\]
Puedes consultar tu trabajo haciendo clic en el botón. También se puede confirmar que los dos enfoques, Solver y cálculo, están de acuerdo.
PASO Proceda a la hoja OutputSide para ver un conjunto familiar de cuatro gráficas.
Como es habitual, los totales están en la parte superior y las curvas promedio y marginales en la parte inferior. Las curvas de costo son bastante similares a las gráficas de maximización de ganancias de salida de la firma de PC, pero las curvas de ingresos son bastante diferentes.
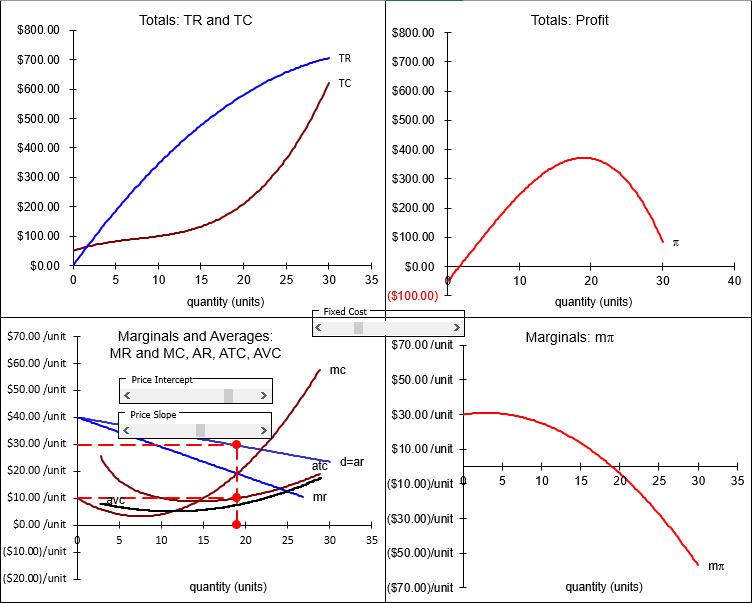
Figura 15.3: Gráficas de maximización de ganancias de salida de monopolio.
Fuente: Monopoly.xls! OutputSide
La gráfica de la esquina inferior izquierda de la Figura 15.3 es la gráfica canónica para un monopolista. Se puede utilizar para encontrar rápidamente\(q \mbox{*}\),\(P \mbox{*}\), y\(\pi \mbox{*}\). A continuación, le indicamos cómo leer y usar el gráfico de monopolio convencional:
Encontrar\(q \mbox{*}\): Elija q donde\(MR = MC\). Esto le da a la mayor diferencia entre TR y TC y lo coloca en la cima de la colina de ganancias (en la gráfica superior derecha).
En\(q \mbox{*}\), viaja recto hacia arriba hasta llegar a la curva de demanda para conseguir\(P \mbox{*}\). Este es el precio más alto que puede obtener el monopolista por el nivel de producción elegido.
Crear el rectángulo de ganancias habitual como\((AR – ATC)q \mbox{*}\). Tiene longitud\(q \mbox{*}\) y altura\(AR - ATC\) (donde\(AR = P\)). El área de este rectángulo es igual a la distancia del segmento de línea entre TR y TC, que es la altura del cerro de beneficio.
Juega con los controles deslizadores para mejorar tu comprensión de los gráficos y las relaciones.
PASO Haga clic en el control deslizante Costo fijo para manipular los costos fijos totales (d en la función de costo cúbico).
Los cambios en los costos fijos no afectan la solución óptima de cantidad y precio del monopolista. Esto es igual que el caso perfectamente competitivo.
PASO Haga clic en el botón; explore los cambios en la intercepción de precios para ver cómo responde la firma. A una intercepción de precios lo suficientemente baja, las ganancias se vuelven negativas y, al igual que una firma de PC\(P < AVC\), si, la firma cerrará.
También se puede controlar el poder de monopolio de la empresa manipulando la pendiente de la curva de demanda inversa.
PASO Establece el deslizador Pendiente de Precio en cero. ¿Qué pasa?
Despojaste el monopolio de su poder de precio y es una firma de PC.
Sin curva de suministro para Monopoly
Los monopolistas no tienen una curva de oferta. Esto parece una declaración extraña ya que los monopolios producen producción y así “abastecen” cualquier bien o servicio del que sean el único vendedor. Pero la clave radica en la definición de una curva de oferta: dado el precio, la curva de oferta da la cantidad que se producirá.
Debido a que una firma de PC es una tomadora de precios, es posible impactar P y ver cómo cambia la salida óptima. Podemos derivar\(q \mbox{*} = f(P, \textrm{ ceteris paribus})\) y esto se llama curva de oferta.
A diferencia de una firma perfectamente competitiva, por la que el precio es exógeno, un monopolio elige el precio. Así, no podemos preguntar: “Dado este precio, ¿cuál es la cantidad óptima suministrada?” Con el precio como variable endógena, no puede servir como variable de choque en un análisis estadístico comparativo.
Podemos (y usted acaba de hacerlo) impactar los parámetros de la curva de demanda de un monopolista como la intercepción y la pendiente, pero esto no es un cambio exógeno en el precio del producto. El experimento de cambiar el precio no puede aplicarse a un monopolista y, por lo tanto, el monopolista no tiene curva de oferta.
Medición del poder monopolista
Otro error común es que el monopolio es cero o uno. De hecho, es un continuum y se puede tener más o menos poder monopolista. Hay varias formas de medirlo.
PASO Proceder a la hoja Lerner.
Esta hoja demuestra el punto de que cuanto más inelástica es la demanda que enfrenta un monopolista, mayor es el poder monopolista. Es decir, desde un punto de vista maximizador de ganancias, es mejor tener un monopolio sobre un producto que todos necesitan desesperadamente (es decir, muy inelástico) que ser el único vendedor de un producto que tenga una curva de demanda de mercado altamente elástica.
Abba Lerner formalizó esta idea en una expresión matemática que lleva su nombre, el Índice Lerner. “Si P = precio y MC = costo marginal, entonces el índice del grado de poder de monopolio lo es”\(\frac{P-MC}{P}\). (Lerner, 1934, p. 169). Esta medida de poder monopolista utiliza la brecha entre P y MC como porcentaje de P.
El Índice Lerner aprovecha que un monopolista elegirá esa cantidad donde\(MR = MC\), luego cobrará el precio más alto posible por esa cantidad. Cuanto mayor sea el precio que se pueda cobrar, más inelástica es la demanda y mayor es el poder monopolista.
La hoja Lerner compara dos monopolios con exactamente la misma estructura de costos (se supone que por simplicidad tiene una constante\(MC = AC\)). Ambos producen la misma cantidad maximizadora de ganancias, pero la Firma 2 enfrenta una curva de demanda más inelástica que la Firma 1 y, por lo tanto, tiene una mayor brecha entre precio y costo marginal.
PASO Haga clic en las celdas B16 e I16 para ver las fórmulas simples para el Índice Lerner.
La idea es que cuanto mayor es la divergencia entre precio y costo marginal, mayor es el poder monopolista. La firma 2 tiene más poder de monopolio que la Firma 1 y más ganancias monopolistas. El Índice Lerner para cada firma refleja esto.
Observe que una firma perfectamente competitiva que establece\(MC = P\) tendrá un Índice Lerner de cero. A medida que el índice se acerca a uno, el poder de monopolio
PASO Cambiar los parámetros de demanda de la Firma 2 a 130 para la intercepción y 20 para la pendiente. El eje y está bloqueado por lo que no se muestran todas las funciones D y MR.
La cantidad óptima sigue siendo 3, pero P y las ganancias son mayores, al igual que el Índice Lerner.
PASO Hacer que la curva de demanda sea más inelástica\(Q=3\) al establecer los parámetros de demanda en 190 y 30.
El P óptimo ha vuelto a aumentar, junto con las ganancias. El Índice Lerner refleja el mayor poder de monopolio.
PASO Una última vez, cambie los parámetros de demanda a 6010 y 1000. El gráfico es difícil de leer porque solo se muestra MR; D está literalmente fuera del gráfico.
La firma 2 continúa produciendo la misma producción que la Firma 1, pero tiene un precio óptimo mucho, mucho más alto y ganancias máximas. Su índice Lerner está cerca de uno. No puede elevarse por encima de uno, pero cuanto más se acerca, mayor es la divergencia de P y MC por lo que mayor es el poder monopolista.
La hoja Lerner también muestra que el Índice Lerner puede expresarse como el recíproco de la elasticidad de precio de la demanda al precio maximizador de ganancias. Los pocos pasos de álgebra necesarios para conectar el Índice Lerner a la elasticidad de precios comienzan en la fila 25.
PASO Vuelva a establecer los parámetros de demanda de Firm 2 a 70 y 10, y luego haga clic en el botón.
Se muestra la elasticidad de precio de la demanda de las dos firmas. Si haces clic en las celdas, puedes ver la fórmula. Observe que el recíproco de la pendiente de la curva de demanda inversa se utiliza para calcular correctamente la elasticidad de precio de la demanda.
La elasticidad de la demanda de la firma 2 al precio maximizador de ganancias es menor que la de la firma 1. Cuanto menor sea la elasticidad de los precios y mayor sea el índice Lerner, mayor será el poder de monopolio de la firma.
PASO Proceda a la hoja de Herfindahl para echar un vistazo rápido a otra forma de medir el poder de monopolio.
En lugar de medir el margen del precio sobre el costo marginal, podemos ver qué tan grandes son las firmas en una industria. Estrictamente hablando, un monopolio es una sola firma por lo que tendría una cuota de mercado del 100%, pero en la práctica, las empresas tienen poder de monopolio a pesar de que técnicamente no son monopolios. Se dice que cualquier firma que se enfrente a una curva de demanda descendente y tenga la capacidad de fijar su precio tiene poder de monopolio.
Si un mercado tiene muchas firmas, cada una con la misma participación en las ventas totales, tenemos una estructura de mercado competitiva. Si, por otro lado, solo existen unas pocas firmas, el mercado se monopoliza. La pregunta es ¿cómo medir el grado de monopolización?
Podemos clasificar las firmas de una industria de mayor a menor participación y luego agregar las acciones de las cuatro firmas más grandes. Esto da la relación de concentración de cuatro firmes en la celda D5. Resulta que esta no es una muy buena manera de distinguir entre industrias concentradas y no concentradas.
El problema es que el ratio de concentración de cuatro firmas no te dice nada sobre los tamaños de las cuatro firmas principales o del resto del mercado. El ratio de concentración de cuatro firmas es del 70%, lo que parece bastante altamente concentrado. La mayor participación de la firma, 30%, es casi un tercio de toda la industria.
PASO Haga clic en el botón.
La relación de concentración de cuatro firmas es la misma que antes (70%), pero esta industria está claramente mucho más concentrada. La Firma A es aún más grande y las demás son pequeñas.
PASO Haga clic en el botón.
La relación de concentración de cuatro firmas es la misma que antes (70%), pero esta industria está claramente menos concentrada. Las cuatro firmas principales son iguales por lo que ninguna firma domina realmente.
La principal virtud de la relación de concentración de cuatro firmas es que es fácil de calcular y entender. Sin embargo, debido a que tenemos tres escenarios con acciones tremendamente diferentes para las cuatro principales empresas que producen el mismo ratio de concentración de cuatro firmas, podemos concluir que esta relación es una mala manera de determinar si las empresas en un mercado se encuentran en un entorno competitivo o monopolístico. La relación de concentración de cuatro firmas puede ser fácil de calcular y entender, pero es incapaz de captar diferencias en la distribución de acciones.
Una mejor manera de juzgar la concentración es a través del Índice Herfindahl. A diferencia del Índice Lerner, existe confusión sobre quién lo inventó. Hirschman concluye: “El resultado neto es que mi índice lleva el nombre ya sea de Gini que no lo inventó en absoluto o de Herfindahl que lo reinventó. Bueno, es un mundo cruel” (Hirschman, 1964, p. 761). A veces se le llama el Índice Herfindahl-Hirschman (HHI).
Afortunadamente, su cómputo es más sencillo que su paternidad. La idea es cuadrar cada acción y suma, así:\[H=\sum_{i=1}^{n}S_i^2\] El índice va de 1/ n a 1 (cuando se utilizan valores decimales de acciones). Cuanto mayor sea el índice, mayor será la concentración. Al cuadrar las acciones, da más peso a firmas más grandes: por ejemplo,\(0.1^2 = 0.01\), mientras\(0.3^2=0.09\).
La hoja de Herfindahl muestra el cómputo. Observe cómo cada valor de la columna B es cuadrado en la columna G. La suma de los cuadrados está en la celda G15 y es el valor del Índice de Herfindahl.
PASO Haga clic en los tres botones uno tras otro para recorrerlos. Observe cómo cambia el Índice de Herfindahl (pero la relación de concentración de cuatro firmas no lo hace).
Para la Distribución A, el valor de H es 0.325. Esto es bastante alto. El valor 0.1375 con Distribución B significa que hay más competencia en este escenario que los otros dos.
El índice de Herfindahl no es perfecto porque ningún número puede describir completamente una distribución completa. Sin embargo, es mejor que la relación de concentración de cuatro firmas y a menudo se usa para medir el grado de competencia en el mercado.
El Departamento de Justicia de los Estados Unidos está encargado de regular la conducta y organización de los negocios. La misión de la División Antimonopolio es promover la competencia económica. Utilizan el Índice Herfindahl como parte de sus Lineamientos de Fusión Horizontal (www.justice.gov/atr/horizontal-merger-guidelines-08192010). Los mercados con un índice Herfindahl inferior a 0.15 están “desconcentrados”, los valores entre 0.15 y 0.25 están “moderadamente concentrados” y cualquier cosa por encima de 0.25 está “altamente concentrada”.
El Departamento de Justicia considera que cualquier propuesta de fusión que incremente el Índice Herfindahl en más de 0.01 (100 puntos en la escala que utilizan) en mercados concentrados es merecedora de escrutinio. Pueden acudir a los tribunales para bloquear fusiones para evitar demasiada concentración. También pueden descomponer empresas que tienen demasiado poder monopolista. Esto se conoce como derecho antimonopolio y forma parte del campo de la economía de la Organización Industrial.
Un enfoque poco convencional
El problema de maximización de ganancias del monopolista también se puede resolver eligiendo P y q simultáneamente sujetos a la restricción de la curva de demanda. Si bien esta no es la forma habitual de enmarcar el problema de optimización del monopolio, permite practicar con el método lagrangeo de resolver problemas de optimización restringidos y leer curvas de isobeneficio.
La solución analítica se basa en reescribir la restricción para que sea igual a cero (\(P-(p_0-p_1q)=0\)), formando el Lagrangean, estableciendo derivadas iguales a cero y resolviendo el sistema de ecuaciones para la solución óptima.
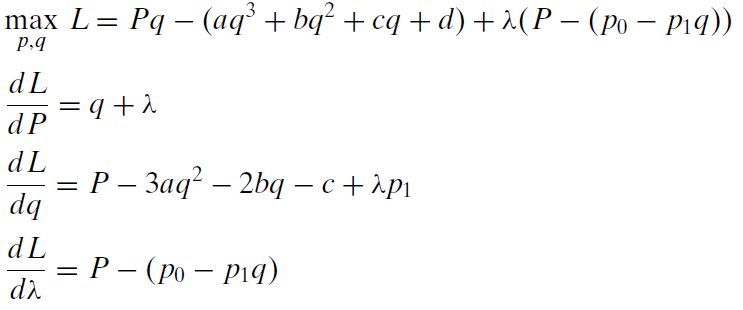
Establezca cada derivada igual a cero y resuelva las tres condiciones de primer orden para\(q \mbox{*}\),\(P \mbox{*}\), y\(\lambda \mbox{*}\). De la primera ecuación,\(\lambda = -q\), sustituir a la segunda ecuación:\[P - 3aq^2 - 2bq - c + [-q] p_1 = 0\] De la tercera condición de primer orden,\(P = p_0 - p_1q\), así\[(p_0 - p_1q) - 3aq^2 - 2bq - c - qp_1 = 0\] Reorganizar los términos para prepararse para el uso de la fórmula cuadrática.
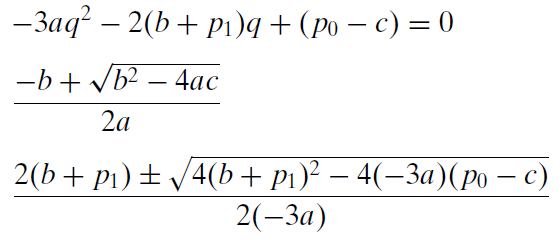
PASO Proceda a la hoja CONOpt para ver fórmulas basadas en la solución Lagrangean comenzando en la celda F24.
Naturalmente, obtenemos la misma respuesta correcta que la versión sin restricciones.
La hoja ConOpt muestra que el monopolio como problema de optimización restringida se puede representar con una gráfica. Las curvas rosadas son curvas de isobeneficio y la línea negra es demanda inversa. La curva MR no se dibuja porque no se utiliza. La firma está tratando de llegar a la isoganancia más alta sin violar la restricción de la curva de demanda. Claramente, los valores de apertura no son óptimos.
PASO Ejecute Solver y obtenga un Informe de Sensibilidad para confirmar que el valor de la estrella lambda es menos la cantidad óptima. Observe cómo se configura el cuadro de diálogo Solver para que Solver elija las celdas B8 y B9 sujetas a la restricción.
Después de ejecutar Solver, la gráfica, reproducida en la Figura 15.4, muestra el resultado de tangencia habitual.
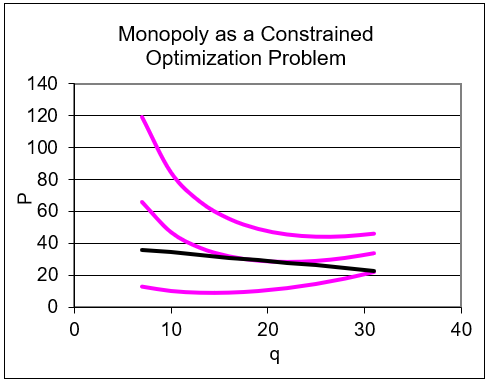
Figura 15.4: La versión de optimización restringida del problema del monopolio.
Fuente: Monopoly.xls! ConOpt
El punto de tangencia proporciona la solución óptima de q y P, mientras que el valor de la curva de isobeneficio en ese punto es el nivel de ganancias.
No se confunda. La versión restringida rara vez se usa. El enfoque convencional es la gráfica canónica de maximización de ganancias de salida (abajo a la izquierda en la Figura 15,2). Esta gráfica muestra la q óptima donde\(MR=MC\) y se muestra fácilmente\(P \mbox{*}\) desde la curva de demanda y\(\pi \mbox{*}\) como un rectángulo.
La Figura 15.4 da la misma solución óptima, pero presenta el problema de una manera diferente. Comprender que la curva de demanda sirve como una restricción al monopolio es útil. El poder monopolista no es infinito. Un monopolista no puede elegir un precio ridículamente alto y una cantidad alta. A medida que el precio sube, la cantidad vendida debe caer.
Fundamentos del monopolio
Un monopolio difiere de una firma perfectamente competitiva en que un monopolista puede elegir la cantidad y el precio, mientras que un competidor perfecto es un tomador de precios. Además, un monopolista tiene una barrera de entrada que le permite mantener ganancias económicas positivas incluso a largo plazo.
Los dos son iguales, sin embargo, en la estructura de costos (como un competidor perfecto, el monopolista deriva su función de costo del problema de minimización de costos de entrada) y el hecho de que busca maximizar las ganancias (donde\(MR = MC\) siempre y cuando\(P>AVC\)).
Representamos la solución óptima del monopolista con una gráfica que superpone D y MR sobre la familia de curvas de costo (MC, ATC y AVC). Al igual que una firma de PC, un monopolista puede sufrir ganancias negativas a corto plazo y cerrará cuando\(P < AVC\).
La gráfica canónica de Monopoly (la gráfica inferior izquierda en la Figura 15.2) pertenece al panteón de gráficas fundamentales en economía. Al igual que las curvas de indiferencia con restricción presupuestal o oferta y demanda, una demanda lineal inversa con sus ingresos marginales asociados mostrando q óptima (en la intersección de MR y MC, por supuesto) y P óptima es una gráfica verdaderamente clásica.
Una forma de medir el poder monopolista es mediante el Índice Lerner. Cuanto mayor sea la brecha entre precio y costo marginal, mayor será el poder de monopolio. Cuanto mayor es la elasticidad de precios de la demanda, menor es el Índice Lerner y más débil es el poder de monopolio.
El Índice Herfindahl es otra forma de medir la fuerza de la monopolización en un mercado. Mide la concentración de la industria. A diferencia del ratio de concentración de cuatro firmas, utiliza las cuotas de mercado de cada empresa para crear un solo número que refleje la concentración de una industria. Las fusiones que impulsan el Índice Herfindahl en más de 0.01 (100 puntos) en mercados concentrados son cuidadosamente escrutadas por el Departamento de Justicia porque se presume que el mercado no será competitivo.
Concluimos este capítulo con un análisis poco convencional. El problema de maximización de ganancias del monopolio se puede lanzar como un problema de optimización restringida. Además de dotar a la práctica del método lagrangeo, esta forma de ver el monopolio deja bastante claro que el monopolista debe obedecer la curva de demanda.
Ejercicios
De Beers es una compañía de fama internacional que tenía el monopolio sobre los diamantes. Google “diamantes sintéticos” para obtener más información. Incluya citas web con evidencia de respaldo en sus respuestas a estas dos preguntas.
¿Cuál era su barrera de entrada cuando tenían monopolio?
¿Qué pasó con su monopolio?
Utilice las Herramientas de Dibujo de Word para representar un monopolio que se cierra a corto plazo. Explique la gráfica.
En la hoja ConOpt, establezca la intercepción de demanda (celda B13) en 9 y el costo fijo (B18) en 180. Ejecute Solver. ¿Por qué Solver genera un resultado miserable? ¿Cuál es la respuesta correcta?
Utilice las herramientas de dibujo de Word para representar el efecto del monopolio desde la perspectiva de maximización de ganancias del lado de entrada. Explique la gráfica.
Pista: Con competencia perfecta,\(L \mbox{*}\) se encuentra donde\(w = MRP\) (donde MRP se basa en el precio dado, constante,\(PxMP\)). Con monopolio, sin embargo, P y MR divergen.
¿El efecto del monopolio en el lado de los insumos es consistente con el efecto del monopolio en el lado de la producción? Explique.
Referencias
El epígrafe es de la página 149 de Hans Brems, Pioneering Economic Theory, 1630—1980: A Mathematical Restatement (1986). Este libro reformula ideas en la historia de la economía en términos matemáticos. Ver los pensamientos de Smith, Ricardo, Marx y otros presentados como modelos matemáticos proporciona una perspectiva poco común.
En el Índice Lerner, véase Abba P. Lerner, “El concepto de monopolio y la medición del poder monopólico”, The Review of Economic Studies, Vol. 1, núm. 3 (junio de 1934), pp. 157—175, www.jstor.org/stable/2967480.
Sobre el Índice Herfindahl, véase Albert O. Hirschman, “La paternidad de un índice”, The American Economic Review, Vol. 54, núm. 5 (septiembre de 1964), p. 761, www.jstor.org/stable/1818582.
Figura 15.1: Un continuo de estructuras de mercado.
botón, intente hacer el problema por su cuenta. Esta es una maximización sin restricciones de una sola variable porque\(P = p_0 - p_1q\) ha sido sustituida en la función de ganancia. Tomar la derivada con respecto a q, ponerla igual a cero, y resolver para q óptima. Sustituir en los valores de los parámetros para convertirlo en un problema concreto facilita la matemática:\[\begin{gathered} %star suppresses line # \max\limits_{q} \pi = (40-0.55)q - (0.04q^3 - 0.9q^2 + 10q + 50)\end{gathered}\]
botón. También se puede confirmar que los dos enfoques, Solver y cálculo, están de acuerdo.
botón; explore los cambios en la intercepción de precios para ver cómo responde la firma. A una intercepción de precios lo suficientemente baja, las ganancias se vuelven negativas y, al igual que una firma de PC\(P < AVC\), si, la firma cerrará.
botón.
botón.
botón.
