Establecimos en el capítulo anterior que, al decidir sobre un producto maximizador de ganancias, cualquier empresa debe producir hasta el punto en que el costo adicional sea igual a los ingresos adicionales de una unidad de producción. Lo que distingue la decisión de oferta para un monopolista de la decisión de oferta del competidor perfecto es que el monopolista enfrenta una demanda en pendiente descendente. Un monopolista es el único proveedor y por lo tanto debe satisfacer toda la demanda del mercado. Esto quiere decir que si se produce más producción, el precio debe caer. Ilustraremos la elección de un beneficio maximizando la producción usando primero un enfoque de costo marginal/ingresos marginales; luego un enfoque de oferta/demanda.
Ingresos marginales y costo marginal
El Cuadro 10.1 muestra los valores de precio y cantidad para una curva de demanda en las columnas 1 y 2. La columna 3 contiene los ingresos por ventas generados en cada salida. Es el producto de precio y cantidad. Dado que el precio denota los ingresos por unidad, a veces se le conoce como ingreso promedio. El ingreso total (TR) alcanza un máximo de 32 dólares, donde se producen 4 unidades de producción. Una mayor producción requiere un precio menor por cada unidad vendida, y en este caso los ingresos caen si la quinta unidad es traída al mercado. A pesar de que la quinta unidad se vende por un precio positivo, el precio de las otras 4 unidades es ahora menor y el efecto neto es reducir los ingresos totales. Este patrón refleja lo que examinamos en el Capítulo 4: A medida que el precio se baja desde el valor más alto posible de 14 dólares (donde se demanda 1 unidad) y la cantidad correspondiente aumenta, los ingresos aumentan, alcanzan su punto máximo y finalmente caen a medida que aumenta la producción. En el Capítulo 4 explicamos que este punto máximo de ingresos ocurre donde la elasticidad del precio es la unidad (-1), en el punto medio de una curva lineal de demanda.
Cuadro 10.1 Un monopolista maximizador de ganancias
| Cantidad |
Precio |
Total |
Marginal |
Marginal |
Total |
Beneficio |
| (Q) |
(P) |
ingresos (TR) |
ingresos (MR) |
costo (MC) |
costo (TC) |
|
| 0 |
16 |
|
|
|
|
|
| 1 |
14 |
14 |
14 |
2 |
2 |
12 |
| 2 |
12 |
24 |
10 |
3 |
5 |
19 |
| 3 |
10 |
30 |
6 |
4 |
9 |
21 |
| 4 |
8 |
32 |
2 |
5 |
14 |
18 |
| 5 |
6 |
30 |
-2 |
6 |
20 |
10 |
| 6 |
4 |
24 |
-6 |
7 |
27 |
-3 |
| 7 |
2 |
14 |
-10 |
8 |
35 |
-21 |
Relacionada con la función de ingresos totales está la función de ingresos marginales. Es la suma de ingresos totales por la venta de una unidad más de la mercancía.
El ingreso marginal es el cambio en los ingresos totales debido a la venta de una unidad más del bien.
El ingreso promedio es el precio por unidad vendida.
El MR en este ejemplo se define en la cuarta columna del Cuadro 10.1. Cuando la cantidad vendida aumenta de 1 unidad a 2 unidades el ingreso total aumenta de $14 a $24. Por lo tanto, el ingreso marginal asociado a la segunda unidad de producción es de $10. Cuando se vende una tercera unidad TR aumenta a $30 y por lo tanto el MR de la tercera unidad es de $6. A medida que aumenta la producción, el MR disminuye y eventualmente se vuelve negativo —en el punto donde el TR es un máximo: Si TR comienza a disminuir entonces los ingresos adicionales son por definición negativos.
La función MR se representa en la Figura 10.4. Se vuelve negativo cuando la salida aumenta de 4 a 5 unidades.
La salida óptima
Este productor tiene una estructura de costos marginales dada en la quinta columna de la tabla, y esta también se grafica en la Figura 10.4. Nuestra regla de maximización de ganancias del Capítulo 8 establece que es óptimo producir una mayor producción siempre y cuando los ingresos adicionales excedan el costo adicional de producción en la siguiente unidad de producción. En mercados perfectamente competitivos el ingreso adicional viene dado por el precio fijo para el productor individual, mientras que para el monopolista el ingreso adicional es el ingreso marginal. En consecuencia, siempre y cuando MR supere a MC para la siguiente unidad, un mayor rendimiento es rentable, pero una vez que MC excede a MR, la producción de unidades adicionales debe cesar.
De la Tabla 10.1 y la Figura 10.4 es claro que la salida óptima es en 3 unidades. La propia tercera unidad arroja una ganancia de 2$, la diferencia entre MR ($6) y MC ($4). Sin embargo, una cuarta unidad reduciría las ganancias en $3, porque el MR ($2) es menor que el MC ($5). ¿Qué precio debe cobrar el productor? El precio, como siempre, viene dado por la función de demanda. A una cantidad vendida de 3 unidades, el precio correspondiente es de $10, lo que arroja ingresos totales de $30.
El beneficio es la diferencia entre los ingresos totales y el costo total. En el Capítulo 8 calculamos el costo total como el costo promedio multiplicado por el número de unidades producidas. También se puede computar como la suma de costos asociados a cada unidad producida: La primera unidad cuesta $2, la segunda $3 y la tercera $4. El costo total de producir 3 unidades es la suma de estos valores en dólares:
. Por lo tanto, la producción maximizadora de ganancias arroja una ganancia de $21 (
).
Oferta y demanda
Al ilustrar el comportamiento del mercado es conveniente describir el comportamiento mediante simples funciones lineales de oferta y demanda que son continuas, en lugar de las funciones 'escalonadas' utilizadas en el ejemplo anterior. Como se explica en el Capítulo 5, al usar curvas continuas para representar un mercado asumimos implícitamente que una unidad de producción puede dividirse en subunidades. En el ejemplo anterior asumimos que las ventas siempre implican una unidad completa del producto que se vende. De hecho muchos bienes se pueden vender en unidades fraccionarias: La gasolina se puede vender en fracciones de litro; las frutas y verduras se pueden vender en fracciones de kilogramo, y así sucesivamente. El cuadro 10.2 a continuación proporciona los datos para nuestro análisis.
Tabla 10.2 Cantidades discretas
| Precio |
Cantidad |
Total |
Total |
Beneficio |
| |
exigió |
ingresos |
costo |
|
| 12 |
0 |
0 |
0 |
0 |
| 11 |
2 |
22 |
1 |
21 |
| 10 |
4 |
40 |
4 |
36 |
| 9 |
6 |
54 |
9 |
45 |
| 8 |
8 |
64 |
16 |
48 |
| 7 |
10 |
70 |
25 |
45 |
| 6 |
12 |
72 |
36 |
36 |
| 5 |
14 |
70 |
49 |
21 |
| 4 |
16 |
64 |
64 |
0 |
| 3 |
18 |
54 |
81 |
-27 |
| 2 |
20 |
40 |
100 |
-60 |
| 1 |
22 |
22 |
121 |
-99 |
| 0 |
24 |
0 |
144 |
-144 |
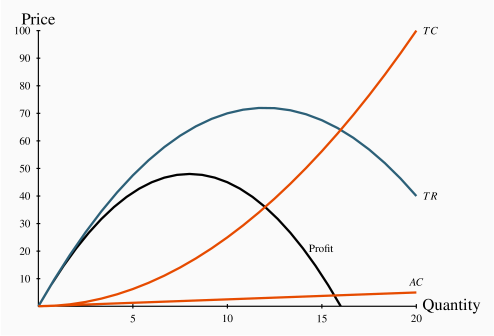
Las dos primeras columnas definen la curva de demanda. El ingreso total es el producto de precio y cantidad y se da en la columna 3. Los datos de costos se dan en la columna 4, y el beneficio — la diferencia entre los ingresos totales y el costo total está en la columna final. Se maximiza el beneficio donde la diferencia entre ingresos y costo es mayor; en este caso donde la salida es de 8 unidades. A menor o mayor rendimiento el beneficio es menor. La Figura 10.5 contiene las curvas que definen el ingreso total (TR), el costo total (TC) y el beneficio. Estas funciones se pueden obtener mapeando todas las combinaciones ingreso-cantidad, las combinaciones costo-cantidad y las combinaciones de beneficio-cantidad como una serie de puntos, y uniendo estos puntos para formar las funciones suaves mostradas. El eje vertical se mide en dólares, el eje horizontal en unidades de salida. Gráficamente, se maximiza el beneficio donde la diferencia en dólares entre TR y TC es mayor; es decir, en la salida donde la distancia vertical entre las dos curvas es mayor. Esta diferencia, que también está definida por la curva de ganancias, se produce a un valor de 8 unidades, correspondiente al resultado en la Tabla 10.2.
En cualquier cantidad inferior a esta producción, la ganancia aumentaría con la producción adicional. Esto se debe a que, a partir de una producción menos que óptima, los ingresos adicionales por el aumento de las ventas superan el aumento del costo asociado con la producción de esas unidades: Dicho de manera diferente, los ingresos marginales excederían al costo marginal. Por el contrario, salidas mayores que el resultado óptimo en una MR menor que la MC asociada. En consecuencia, dado que las salidas donde MR > MC son demasiado bajas, y las salidas donde MR < MC son demasiado altas, el óptimo debe ser donde el MR = MC. De ahí que la igualdad entre MR y MC esté implícita en este diagrama en la salida donde la diferencia entre TR y TC es mayor.
Obsérvese finalmente que los ingresos totales se maximizan donde la curva TR alcanza un pico. En este ejemplo eso ocurre a un valor de 12 unidades de salida. Esto es de anticiparse, como aprendimos en el Capítulo 4, porque el punto medio del horario de demanda en la Tabla 10.2 ocurre a ese valor.
La Figura 10.6 muestra la curva de demanda para el mercado, la curva MR y las curvas MC y AC del monopolista. Considere primero la curva de ingresos marginales. En contraste con el ejemplo anterior, donde solo se podían vender unidades enteras o enteras, en este ejemplo las unidades se pueden vender en cantidades fraccionarias, y la curva MR debe reflejar esto. Para determinar la posición de la curva MR, tenga en cuenta que con una curva de demanda de línea recta el ingreso total es un máximo en el punto medio de la curva de demanda. Cualquier incremento en la producción da como resultado una reducción de los ingresos: Dicho de manera diferente, los ingresos marginales se vuelven negativos en ese producto. Hasta esa salida el MR es positivo, como se ilustra en la Figura 10.3. En consecuencia, la curva MR debe intersectar el eje de cantidad a medio camino entre cero y la intersección del eje horizontal de la curva de demanda. Geométricamente, dado que el MR interseca el eje de cantidad a mitad de camino a la intersección horizontal de la curva de demanda, debe tener una pendiente que sea el doble de la pendiente de la curva de demanda.
Al observar los datos en las columnas 1 y 2 de la tabla, las intercepciones de la curva de demanda son
, y desde la discusión anterior la curva MR tiene intercepciones
. El AC se obtiene dividiendo TC por salida en el Cuadro 10.2, y el MC también se puede calcular como el cambio en el costo total dividido por el cambio en la salida del Cuadro 10.2. El resultado de estos cálculos se muestra en la Figura 10.6.
El beneficio maximizando la salida es de 8 unidades, donde MC = MR. El precio al que se pueden vender 8 unidades se lee en la curva de demanda , o la primera columna del Cuadro 10.2. Es de $8. Y, como era de esperar, esta combinación precio-cantidad maximiza las ganancias. El Cuadro 10.2 indica que la ganancia se maximiza en $48, en q =8.
Elasticidad de demanda e ingresos marginales
Hemos demostrado anteriormente que la curva MR corta el eje horizontal en una cantidad donde la elasticidad de la demanda es la unidad. Sabemos por el Capítulo 4 que la demanda es elástica en puntos de la curva de demanda por encima de este punto unidad-elástico. Además, dado que la intersección de MR y MC debe estar a un valor positivo en dólares (MC no puede ser negativo), entonces debe darse el caso de que el precio maximizador de ganancias para un monopolista siempre se encuentre en el segmento elástico de la curva de demanda.
Una representación gráfica general
En la Figura 10.7 generalizamos la representación gráfica del beneficio monopolista maximizando la producción al permitir que las curvas MC y ATC sean no lineales. La salida óptima está en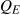
, donde MR = MC, y el precio
sostiene esa producción. Con el costo promedio conocido, el beneficio por unidad es AB, y por lo tanto el beneficio total es este margen multiplicado por el número de unidades vendidas,.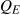
El beneficio total es por lo tanto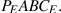
Tenga en cuenta que el monopolista no siempre puede obtener ganancias. Las pérdidas podrían resultar en la Figura 10.7 si los costos promedio aumentaran de manera que el ATC estuviera en todas partes por encima de la curva de demanda, o si la curva de demanda bajara a estar en todas partes por debajo de la curva ATC. A más largo plazo la monopolista tendría que o bien reducir costos o quizás estimular la demanda a través de la publicidad si quería seguir operando.
