12.1: Describir variables individuales
- Page ID
- 144572
La estadística descriptiva se refiere a un conjunto de técnicas para resumir y mostrar datos. Supongamos aquí que los datos son cuantitativos y consisten en puntuaciones en una o más variables para cada uno de los diversos participantes del estudio. Aunque en la mayoría de los casos la pregunta principal de investigación será sobre una o más relaciones estadísticas entre variables, también es importante describir cada variable individualmente. Por esta razón, comenzamos por observar algunas de las técnicas más comunes para describir variables individuales.
La distribución de una variable
Cada variable tiene una distribución, que es la forma en que las puntuaciones se distribuyen entre los niveles de esa variable. Por ejemplo, en una muestra de 100 universitarios, la distribución de la variable “número de hermanos” podría ser tal que 10 de ellos no tengan hermanos, 30 tengan un hermano, 40 tengan dos hermanos, y así sucesivamente. En la misma muestra, la distribución de la variable “sexo” podría ser tal que 44 tengan una puntuación de “masculino” y 56 tengan una puntuación de “femenino”.
Tablas de Frecuencia
Una forma de mostrar la distribución de una variable es en una tabla de frecuencias. La tabla\(\PageIndex{1}\), por ejemplo, es una tabla de frecuencias que muestra una distribución hipotética de las puntuaciones en la Escala de Autoestima de Rosenberg para una muestra de 40 estudiantes universitarios. La primera columna enumera los valores de la variable, las puntuaciones posibles en la escala de Rosenberg, y la segunda columna enumera la frecuencia de cada puntaje. Esta tabla muestra que hubo tres estudiantes que tenían puntuaciones de autoestima de 24, cinco que tenían puntuaciones de autoestima de 23, y así sucesivamente. A partir de una tabla de frecuencias como esta, se pueden ver rápidamente varios aspectos importantes de una distribución, incluyendo el rango de puntuaciones (de 15 a 24), las puntuaciones más y menos comunes (22 y 17, respectivamente), y cualquier puntaje extremo que se destaque del resto.
| Autoestima | Frecuencia |
|---|---|
| 24 | 3 |
| 23 | 5 |
| 22 | 10 |
| 21 | 8 |
| 20 | 5 |
| 19 | 3 |
| 18 | 3 |
| 17 | 0 |
| 16 | 2 |
| 15 | 1 |
Hay algunos otros puntos que vale la pena destacar sobre las tablas de frecuencias. Primero, los niveles listados en la primera columna suelen ir desde los más altos en la parte superior hasta los más bajos en la parte inferior, y generalmente no se extienden más allá de las puntuaciones más altas y más bajas en los datos. Por ejemplo, aunque las puntuaciones en la escala de Rosenberg pueden variar de un máximo de 30 a un mínimo de 0, la Tabla\(\PageIndex{1}\) solo incluye niveles de 24 a 15 porque ese rango incluye todas las puntuaciones de este conjunto de datos en particular. Segundo, cuando hay muchas puntuaciones diferentes en una amplia gama de valores, a menudo es mejor crear una tabla de frecuencias agrupadas, en la que la primera columna enumera rangos de valores y la segunda columna enumera la frecuencia de puntuaciones en cada rango. La tabla\(\PageIndex{2}\), por ejemplo, es una tabla de frecuencias agrupadas que muestra una distribución hipotética de tiempos de reacción simples para una muestra de 20 participantes. En una tabla de frecuencias agrupadas, todos los rangos deben ser de igual ancho, y generalmente hay entre cinco y 15 de ellos. Por último, también se pueden utilizar tablas de frecuencias para variables categóricas, en cuyo caso los niveles son etiquetas de categoría. El orden de las etiquetas de categoría es algo arbitrario, pero a menudo se listan desde las más frecuentes en la parte superior hasta las menos frecuentes en la parte inferior.
| Tiempo de reacción (ms) | Frecuencia |
|---|---|
| 241—260 | 1 |
| 221—240 | 2 |
| 201—220 | 2 |
| 181—200 | 9 |
| 161—180 | 4 |
| 141—160 | 2 |
Histogramas
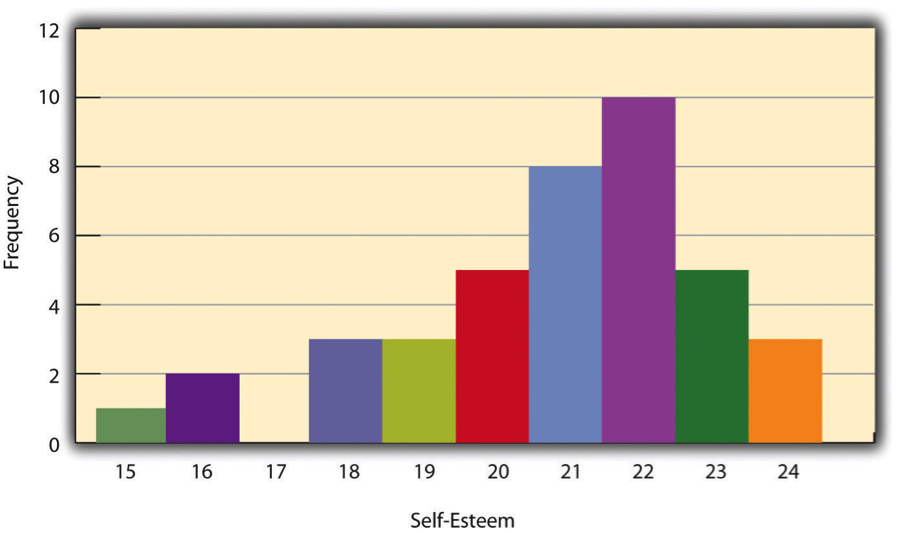
Un histograma es una visualización gráfica de una distribución. Presenta la misma información que una tabla de frecuencias pero de una manera aún más rápida y fácil de captar. El histograma de la Figura\(\PageIndex{1}\) presenta la distribución de las puntuaciones de autoestima en la Tabla\(\PageIndex{1}\). El eje x del histograma representa la variable y el eje y representa la frecuencia. Por encima de cada nivel de la variable en el eje x hay una barra vertical que representa el número de individuos con esa puntuación. Cuando la variable es cuantitativa, como en este ejemplo, no suele haber hueco entre las barras. Cuando la variable es categórica, sin embargo, suele haber una pequeña brecha entre ellas. (La brecha a 17 en este histograma refleja el hecho de que no hubo puntuaciones de 17 en este conjunto de datos).
Formas de Distribución
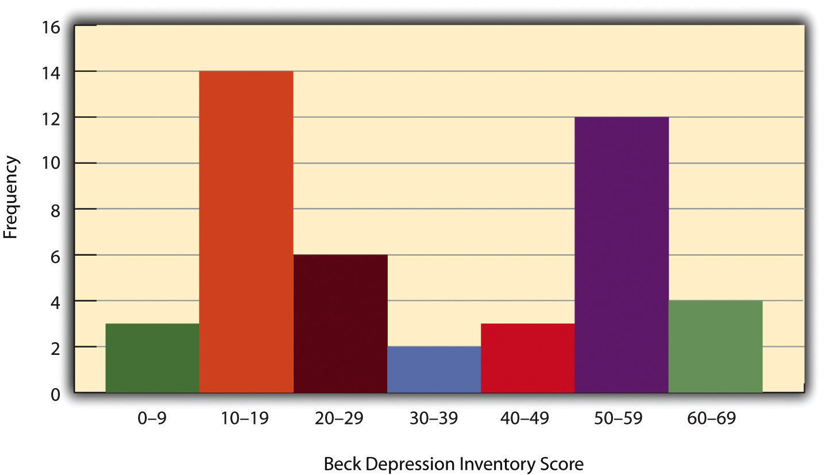
Cuando la distribución de una variable cuantitativa se muestra en un histograma, ésta tiene una forma. La forma de la distribución de las puntuaciones de autoestima en la Figura\(\PageIndex{1}\) es típica. Hay un pico en algún lugar cerca de la mitad de la distribución y “colas” que se estrecha en cualquier dirección desde el pico. La distribución de la Figura\(\PageIndex{1}\) es unimodal, lo que significa que tiene un pico distinto, pero las distribuciones también pueden ser bimodales, lo que significa que tienen dos picos distintos. La figura\(\PageIndex{2}\), por ejemplo, muestra una hipotética distribución bimodal de las puntuaciones en el Inventario de Depresión de Beck. Las distribuciones también pueden tener más de dos picos distintos, pero estos son relativamente raros en la investigación psicológica.
Otra característica de la forma de una distribución es si es simétrica o sesgada. La distribución en el centro de la Figura\(\PageIndex{3}\) es simétrica. Sus mitades izquierda y derecha son imágenes especuladas entre sí. La distribución de la izquierda está sesgada negativamente, con su pico desplazado hacia el extremo superior de su rango y una cola negativa relativamente larga. La distribución a la derecha está sesgada positivamente, con su pico hacia el extremo inferior de su rango y una cola positiva relativamente larga.

Un valor atípico es una puntuación extrema que es mucho mayor o menor que el resto de las puntuaciones en la distribución. A veces los valores atípicos representan puntuaciones verdaderamente extremas en la variable de interés. Por ejemplo, en el Inventario de Depresión de Beck, una sola persona clínicamente deprimida podría ser un valor atípico en una muestra de compañeros por lo demás felices y de alto funcionamiento. Sin embargo, los valores atípicos también pueden representar errores o malentendidos por parte del investigador o participante, mal funcionamiento del equipo o problemas similares. Más adelante en este capítulo diremos más sobre cómo interpretar los valores atípicos y qué hacer al respecto.
Medidas de Tendencia Central y Variabilidad
También es útil poder describir las características de una distribución con mayor precisión. Aquí analizamos cómo hacerlo en términos de dos características importantes: su tendencia central y su variabilidad.
Tendencia Central
La tendencia central de una distribución es su centro, el punto alrededor del cual las puntuaciones en la distribución tienden a agruparse. (Otro término para tendencia central es promedio.) Mirando hacia atrás en Figura\(\PageIndex{1}\), por ejemplo, podemos ver que los puntajes de autoestima tienden a agruparse alrededor de los valores de 20 a 22. Aquí consideraremos las tres medidas más comunes de tendencia central: la media, la mediana y el modo.
La media de una distribución (M simbolizada) es la suma de las puntuaciones dividida por el número de puntajes. Es un promedio. Como fórmula, se ve así:
\[M=\dfrac{\displaystyle \sum X}{N}\]
En esta fórmula, el símbolo σ (la letra griega sigma) es el signo de suma y significa sumar a través de los valores de la variable X. N representa el número de puntajes. La media es, con mucho, la medida más común de tendencia central, y existen algunas buenas razones para ello. Por lo general, proporciona una buena indicación de la tendencia central de una distribución, y es fácilmente entendida por la mayoría de las personas. Además, la media tiene propiedades estadísticas que la hacen especialmente útil en la realización de estadísticas inferenciales.
Una alternativa a la media es la mediana. La mediana es la puntuación media en el sentido de que la mitad de las puntuaciones en la distribución son menores que ella y la mitad son mayores que ella. La forma más sencilla de encontrar la mediana es organizar las puntuaciones de menor a mayor y ubicar la puntuación en el medio. Consideremos, por ejemplo, el siguiente conjunto de siete puntuaciones:
8 4 12 14 3 2 3
Para encontrar la mediana, simplemente reorganice los puntajes de menor a mayor y ubique el que está en el medio.
2 3 3 4 8 12 14
En este caso, la mediana es 4 porque hay tres puntuaciones menores que 4 y tres puntuaciones superiores a 4. Cuando hay un número par de puntajes, hay dos puntajes a mitad de la distribución, en cuyo caso la mediana es el valor a mitad de camino entre ellas. Por ejemplo, si tuviéramos que sumar una puntuación de 15 al conjunto de datos anterior, habría dos puntuaciones (tanto 4 como 8) a mitad de la distribución, y la mediana estaría a mitad de camino entre ellas (6).
Una medida final de la tendencia central es el modo. El modo es el puntaje más frecuente en una distribución. En la distribución de la autoestima presentada en Tabla\(\PageIndex{1}\) y Figura\(\PageIndex{1}\), por ejemplo, el modo es 22. Más alumnos tenían esa puntuación que cualquier otro. El modo es la única medida de tendencia central que también se puede utilizar para variables categóricas.
En una distribución unimodal y simétrica, la media, la mediana y el modo estarán muy cerca entre sí en el pico de la distribución. En una distribución bimodal o asimétrica, la media, la mediana y el modo pueden ser bastante diferentes. En una distribución bimodal, la media y la mediana tenderán a estar entre los picos, mientras que el modo estará en el pico más alto. En una distribución sesgada, la media diferirá de la mediana en la dirección del sesgo (es decir, la dirección de la cola más larga). Para distribuciones altamente sesgadas, la media se puede tirar hasta el momento en la dirección del sesgo que ya no es una buena medida de la tendencia central de esa distribución. Imagine, por ejemplo, un conjunto de cuatro tiempos de reacción simples de 200, 250, 280 y 250 milisegundos (ms). La media es de 245 ms. Pero la adición de una puntuación más de 5,000 ms —quizás porque el participante no estaba prestando atención— elevaría la media a mil 445 ms. Esta medida de tendencia central no sólo es mayor al 80% de las puntuaciones en la distribución, sino que tampoco parece representar muy bien el comportamiento de nadie en la distribución. Es por ello que los investigadores suelen preferir la mediana para distribuciones altamente sesgadas (como distribuciones de tiempos de reacción).
Tenga en cuenta, sin embargo, que no está obligado a elegir una sola medida de tendencia central en el análisis de sus datos. Cada uno proporciona información ligeramente diferente, y todos ellos pueden ser útiles.
Medidas de Variabilidad
La variabilidad de una distribución es la medida en que las puntuaciones varían en torno a su tendencia central. Consideremos las dos distribuciones de la Figura\(\PageIndex{4}\), las cuales tienen la misma tendencia central. La media, mediana y modo de cada distribución son 10. Observe, sin embargo, que las dos distribuciones difieren en términos de su variabilidad. El superior tiene una variabilidad relativamente baja, con todos los puntajes relativamente cerca del centro. El inferior tiene una variabilidad relativamente alta, con los puntajes se distribuyen en un rango mucho mayor.

Una simple medida de variabilidad es el rango, que es simplemente la diferencia entre las puntuaciones más altas y más bajas en la distribución. El rango de las puntuaciones de autoestima en la Tabla\(\PageIndex{1}\), por ejemplo, es la diferencia entre la puntuación más alta (24) y la puntuación más baja (15). Es decir, el rango es 24 − 15 = 9. Aunque el rango es fácil de calcular y entender, puede ser engañoso cuando hay valores atípicos. Imagínese, por ejemplo, un examen en el que todos los alumnos obtuvieron calificaciones entre 90 y 100. Tiene un rango de 10. Pero si hubiera un solo estudiante que obtuvo 20, el rango aumentaría a 80, dando la impresión de que las puntuaciones eran bastante variables cuando de hecho solo un estudiante difería sustancialmente del resto.
Con mucho, la medida de variabilidad más común es la desviación estándar. La desviación estándar de una distribución es la distancia promedio entre las puntuaciones y la media. Por ejemplo, las desviaciones estándar de las distribuciones en la Figura\(\PageIndex{4}\) son 1.69 para la distribución superior y 4.30 para la inferior. Es decir, mientras que las puntuaciones en la distribución superior difieren de la media en alrededor de 1.69 unidades en promedio, las puntuaciones en la distribución inferior difieren de la media en aproximadamente 4.30 unidades en promedio.
El cálculo de la desviación estándar implica una ligera complicación. Específicamente, implica encontrar la diferencia entre cada puntaje y la media, cuadrar cada diferencia, encontrar la media de estas diferencias cuadradas y finalmente encontrar la raíz cuadrada de esa media. La fórmula se ve así:
\[S D=\sqrt{\frac{\displaystyle \sum (X-M)^{2}}{N}}\]
Los cálculos para la desviación estándar se ilustran para un pequeño conjunto de datos en la Tabla\(\PageIndex{3}\). La primera columna es un conjunto de ocho puntuaciones que tiene una media de 5. La segunda columna es la diferencia entre cada puntaje y la media. La tercera columna es el cuadrado de cada una de estas diferencias. Observe que aunque las diferencias pueden ser negativas, las diferencias cuadradas son siempre positivas, lo que significa que la desviación estándar es siempre positiva. En la parte inferior de la tercera columna se encuentra la media de las diferencias cuadradas, que también se denomina varianza (simbolizada\(SD\) 2). Aunque la varianza es en sí misma una medida de variabilidad, generalmente juega un papel más importante en la estadística inferencial que en la estadística descriptiva. Finalmente, por debajo de la varianza se encuentra la raíz cuadrada de la varianza, que es la desviación estándar.
| \(X\) | \(X_M\) | \((X − M)^2\) |
|---|---|---|
| \ (X\)” style="vertical-align:middle; ">3 | \ (X_M\)” style="vertical-align:middle; ">−2 | \ ((X − M) ^2\)” style="vertical-align:middle; ">4 |
| \ (X\)” style="vertical-align:middle; ">5 | \ (X_M\)” style="vertical-align:middle; ">0 | \ ((X − M) ^2\)” style="vertical-align:middle; ">0 |
| \ (X\)” style="vertical-align:middle; ">4 | \ (X_M\)” style="vertical-align:middle; ">−1 | \ ((X − M) ^2\)” style="vertical-align:middle; ">1 |
| \ (X\)” style="vertical-align:middle; ">2 | \ (X_M\)” style="vertical-align:middle; ">−3 | \ ((X − M) ^2\)” style="vertical-align:middle; ">9 |
| \ (X\)” style="vertical-align:middle; ">7 | \ (X_M\)” style="vertical-align:middle; ">2 | \ ((X − M) ^2\)” style="vertical-align:middle; ">4 |
| \ (X\)” style="vertical-align:middle; ">6 | \ (X_M\)” style="vertical-align:middle; ">1 | \ ((X − M) ^2\)” style="vertical-align:middle; ">1 |
| \ (X\)” style="vertical-align:middle; ">5 | \ (X_M\)” style="vertical-align:middle; ">0 | \ ((X − M) ^2\)” style="vertical-align:middle; ">0 |
| \ (X\)” style="vertical-align:middle; ">8 | \ (X_M\)” style="vertical-align:middle; ">3 | \ ((X − M) ^2\)” style="vertical-align:middle; ">9 |
| \ (X\)” style="vertical-align:middle; "> M = 5 | \ (X_M\)” style="vertical-align:middle; "> | \ ((X − M) ^2\)” style="vertical-align:middle; "> SD 2 =28/8=3.50 |
| \ (X\)” style="vertical-align:middle; "> | \ (X_M\)” style="vertical-align:middle; "> | \ ((X − M) ^2\)” style="vertical-align:middle; "> SD =√3.50=1.87 |
Rangos percentiles y puntuaciones z
En muchas situaciones, es útil tener una manera de describir la ubicación de una partitura individual dentro de su distribución. Un enfoque es el rango percentil. El rango percentil de una puntuación es el porcentaje de puntajes en la distribución que son inferiores a ese puntaje. Consideremos, por ejemplo, la distribución en la Tabla\(\PageIndex{1}\). Para cualquier puntaje en la distribución, podemos encontrar su rango de percentil contando el número de puntajes en la distribución que son inferiores a ese puntaje y convirtiendo ese número a un porcentaje del número total de puntajes. Observe, por ejemplo, que cinco de los estudiantes representados por los datos en Tabla\(\PageIndex{1}\) tuvieron puntuaciones de autoestima de 23. En esta distribución, 32 de las 40 puntuaciones (80%) son inferiores a 23. Así cada uno de estos alumnos tiene un rango percentil de 80. (También se puede decir que anotaron “al percentil 80”). Los rangos percentiles se utilizan a menudo para reportar los resultados de pruebas estandarizadas de habilidad o logro. Si tu rango percentil en una prueba de habilidad verbal fuera 40, por ejemplo, esto significaría que obtuviste una puntuación superior al 40% de las personas que tomaron la prueba.
Otro enfoque es la puntuación z. La puntuación z para un individuo en particular es la diferencia entre la puntuación de ese individuo y la media de la distribución, dividida por la desviación estándar de la distribución:
\[z= \dfrac{X−M}{SD}\]
Una puntuación z indica qué tan por encima o por debajo de la media está una puntuación bruta, pero lo expresa en términos de la desviación estándar. Por ejemplo, en una distribución de puntuaciones del cociente de inteligencia (CI) con una media de 100 y una desviación estándar de 15, una puntuación de CI de 110 tendría una puntuación z de (110 − 100)/15 = +0.67. Es decir, una puntuación de 110 es 0.67 desviaciones estándar (aproximadamente dos tercios de una desviación estándar) por encima de la media. De igual manera, una puntuación bruta de 85 tendría una puntuación z de (85 − 100)/15 = −1.00. Es decir, una puntuación de 85 es una desviación estándar por debajo de la media.
Hay varias razones por las que las puntuaciones z son importantes. Nuevamente, proporcionan una manera de describir dónde se encuentra la puntuación de un individuo dentro de una distribución y en ocasiones se utilizan para reportar los resultados de pruebas estandarizadas. También proporcionan una forma de definir los valores atípicos. Por ejemplo, los valores atípicos a veces se definen como puntuaciones que tienen puntuaciones z menores de −3.00 o mayores que +3.00. En otras palabras, se definen como puntuaciones que son más de tres desviaciones estándar de la media. Por último, las puntuaciones z juegan un papel importante en la comprensión y computación de otras estadísticas, como veremos en breve.


