12.2: Describir las relaciones estadísticas

Objetivos de aprendizaje

1. Describir las diferencias entre grupos en términos de sus medias y desviaciones estándar, y en términos de la d de Cohen.
2. Describir las correlaciones entre variables cuantitativas en términos de r de Pearson.

Como hemos visto a lo largo de este libro, las preguntas de investigación más interesantes en psicología son sobre las relaciones estadísticas entre variables. En esta sección, revisamos las dos formas básicas de relación estadística introducidas anteriormente en el libro, las diferencias entre grupos o condiciones y las relaciones entre variables cuantitativas, y consideramos cómo describirlas con más detalle.

Diferencias entre grupos o condiciones

Las diferencias entre grupos o condiciones generalmente se describen en términos de la media y desviación estándar de cada grupo o condición. Por ejemplo, Thomas Ollendick y sus colegas realizaron un estudio en el que evaluaron dos tratamientos de una sesión para fobias simples en niños (Ollendick et al., 2009) ^[1]. Asignaron aleatoriamente a niños con un miedo intenso (por ejemplo, a perros) a una de tres condiciones. En la condición de exposición, los niños realmente se enfrentaron al objeto de su miedo bajo la guía de un terapeuta capacitado. En la condición educativa, aprendieron sobre las fobias y algunas estrategias para afrontarlas. En la condición de control de lista de espera, estaban esperando recibir un tratamiento una vez finalizado el estudio. La severidad de la fobia de cada niño fue luego calificada en una escala de 1 a 8 por un clínico que no sabía qué tratamiento había recibido el niño. (Esta fue una de varias variables dependientes). La calificación media de miedo en la condición de educación fue de 4.83 con una desviación estándar de 1.52, mientras que la calificación de miedo promedio en la condición de exposición fue de 3.47 con una desviación estándar de 1.77. La puntuación media de miedo en la condición testigo fue de 5.56 con una desviación estándar de 1.21. Es decir, ambos tratamientos funcionaron, pero el tratamiento de exposición funcionó mejor que el tratamiento educativo. Como hemos visto, las diferencias entre medias de grupo o condición se pueden presentar en un gráfico de barras como el de la Figura\(\PageIndex{1}\), donde las alturas de las barras representan las medias de grupo o condición. En breve veremos más de cerca la creación de gráficos de barras al estilo de la Asociación Americana de Psicología (APA).

Figura\(\PageIndex{1}\): Gráfico de barras que muestra las calificaciones medias de fobia a los médicos para niños en dos condiciones de tratamiento

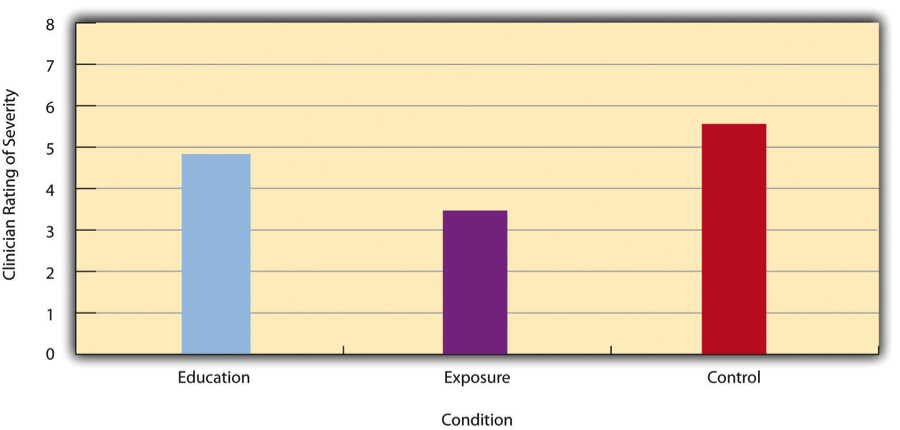
También es importante poder describir la fuerza de una relación estadística, a la que a menudo se le conoce como el tamaño del efecto. La medida más utilizada del tamaño del efecto para las diferencias entre medias de grupo o condición se llama d de Cohen, que es la diferencia entre las dos medias dividida por la desviación estándar:

\[d= \dfrac{M_1 −M_2}{SD}\]

En esta fórmula, realmente no importa cuál es la media\(M_1\) y cuál es\(M_2\). Si hay un grupo de tratamiento y un grupo control, la media del grupo de tratamiento suele ser M 1 y la media del grupo control es\(M_2\). De lo contrario, la media mayor suele ser\(M_1\) y la media más pequeña\(M_2\) para que la d de Cohen resulte ser positiva. En efecto, los valores d de Cohen deben ser siempre positivos por lo que es la diferencia absoluta entre las medias lo que se considera en el numerador. La desviación estándar en esta fórmula suele ser una especie de promedio de las dos desviaciones estándar de grupo llamada desviación estándar agrupada dentro de los grupos. Para calcular la desviación estándar agrupada dentro de grupos, agregue la suma de las diferencias cuadradas para el Grupo 1 a la suma de las diferencias cuadradas para el Grupo 2, divida esta por la suma de los dos tamaños de muestra y luego tome la raíz cuadrada de esa. Informalmente, sin embargo, la desviación estándar de cualquiera de los grupos puede ser utilizada en su lugar.

Conceptualmente, la d de Cohen es la diferencia entre las dos medias expresadas en unidades de desviación estándar. (Observe su similitud con una puntuación z, que expresa la diferencia entre una puntuación individual y una media en unidades de desviación estándar). Una d de Cohen de 0.50 significa que las medias de dos grupos difieren en 0.50 desviaciones estándar (media desviación estándar). Una d de Cohen de 1.20 significa que difieren en 1.20 desviaciones estándar. Pero, ¿cómo debemos interpretar estos valores en términos de la fuerza de la relación o el tamaño de la diferencia entre las medias? \(\PageIndex{1}\)En la tabla se presentan algunas pautas para interpretar los valores d de Cohen en la investigación psicológica (Cohen, 1992) ^[2]. Los valores cercanos a 0.20 se consideran pequeños, los valores cercanos a 0.50 se consideran medianos y los valores cercanos a 0.80 se consideran grandes. Así, un valor d de Cohen de 0.50 representa una diferencia de tamaño mediano entre dos medias, y un valor d de Cohen de 1.20 representa una diferencia muy grande en el contexto de la investigación psicológica. En la investigación de Ollendick y sus colegas, hubo una gran diferencia (d = 0.82) entre las condiciones de exposición y educación.

Tabla\(\PageIndex{1}\): Directrices para referirse a los valores d de Cohen y r de Pearson como “Fuerte”, “Medio” o “Débil”

Fuerza de la relación	^D de Cohen	^R de Pearson
fuerte/grande	0.80	± 0.50
Mediano	0.50	± 0.30
Débil/pequeño	0.20	± 0.10

La d de Cohen es útil porque tiene el mismo significado independientemente de la variable que se compara o de la escala en la que se midió. Una d de Cohen de 0.20 significa que las dos medias grupales difieren en 0.20 desviaciones estándar, ya sea que estemos hablando de puntajes en la escala de autoestima de Rosenberg, tiempo de reacción medido en milisegundos, número de hermanos o presión arterial diastólica medida en milímetros de mercurio. Esto no solo facilita que los investigadores se comuniquen entre sí sobre sus resultados, sino que también permite combinar y comparar resultados a través de diferentes estudios utilizando diferentes medidas.

Tenga en cuenta que el término tamaño del efecto puede ser engañoso porque sugiere una relación causal, que la diferencia entre los dos medios es un “efecto” de estar en un grupo o condición en oposición a otra. Imagínese, por ejemplo, un estudio que muestre que un grupo de usuarios es más feliz en promedio que un grupo de no practicantes, con un “tamaño de efecto” de d = 0.35. Si el estudio fue un experimento, con participantes asignados aleatoriamente a condiciones de ejercicio y sin ejercicio, entonces se podría concluir que el ejercicio causó un aumento de felicidad de pequeño a mediano tamaño. Sin embargo, si el estudio fue transversal, entonces solo se podría concluir que los usuarios estaban más felices que los no practicantes en una cantidad pequeña a mediana. En otras palabras, el simple hecho de llamar a la diferencia un “tamaño de efecto” no hace que la relación sea causal.

Diferencias de sexo expresadas como d de Cohen

La investigadora Janet Shibley Hyde ha examinado los resultados de numerosos estudios sobre diferencias psicológicas de sexo y ha expresado los resultados en términos de d de Cohen (Hyde, 2007) ^[3]. A continuación se presentan algunos de los valores que ha encontrado, promediando a través de varios estudios en cada caso. (Tenga en cuenta que debido a que siempre trata la media para los hombres como M 1 y la media para las mujeres como M 2, los valores positivos indican que los hombres puntúan más altos y los valores negativos indican que las mujeres puntúan más altas).

Resolución matemática de problemas	+0.08
Comprensión lectora	−0.09
Sonriente	−0.40
Agresión	+0.50
Actitudes hacia el sexo casual	+0.81
Efectividad del liderazgo	−0.02

Hyde señala que aunque hombres y mujeres difieren en gran medida en algunas variables (por ejemplo, actitudes hacia el sexo casual), difieren solo en una pequeña cantidad en la gran mayoría. En muchos casos, la d de Cohen es inferior a 0.10, lo que ella denomina una diferencia “trivial”. (La diferencia de locución discutida en el Capítulo 1 también fue trivial: d = 0.06.) Aunque investigadores y no investigadores a menudo enfatizan las diferencias de sexo, Hyde ha argumentado que tiene al menos tanto sentido pensar en hombres y mujeres como fundamentalmente similares. Ella se refiere a esto como la “hipótesis de las similitudes de género”.

Correlaciones entre variables cuantitativas

Como hemos visto a lo largo del libro, muchas relaciones estadísticas interesantes toman la forma de correlaciones entre variables cuantitativas. Por ejemplo, los investigadores Kurt Carlson y Jacqueline Conard realizaron un estudio sobre la relación entre la posición alfabética de la primera letra de los apellidos de las personas (de A = 1 a Z = 26) y la rapidez con la que esas personas respondieron a las apelaciones de los consumidores (Carlson & Conard, 2011) ^[4] . En un estudio, enviaron correos electrónicos a un grupo numeroso de estudiantes de MBA, ofreciendo boletos de basquetbol gratis de una oferta limitada. El resultado fue que cuanto más hacia el final del alfabeto estaban los apellidos de los estudiantes, más rápido tendían a responder. Estos resultados se resumen en la Tabla\(\PageIndex{2}\).

Tabla\(\PageIndex{2}\): Gráfico de líneas que muestra la relación entre la posición alfabética de los apellidos de las personas y la rapidez con la que esas personas responden a las ofertas de bienes de consumo

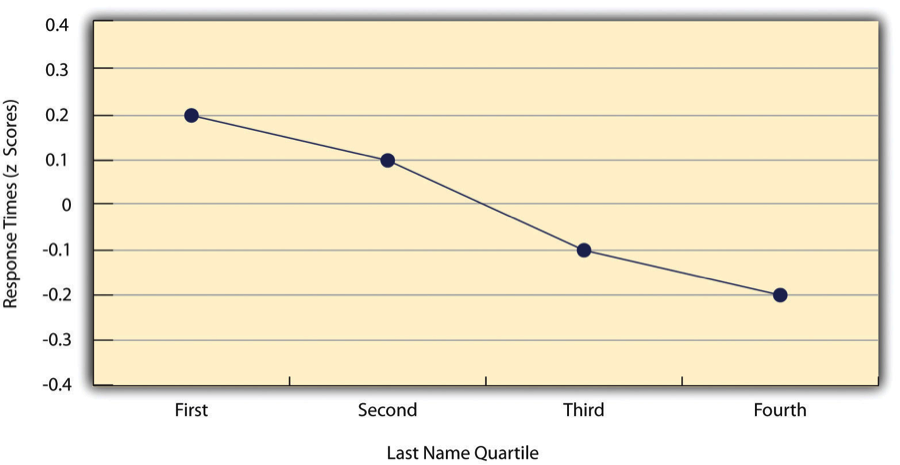
Tales relaciones se presentan a menudo usando gráficos de líneas o diagramas de dispersión, que muestran cómo el nivel de una variable difiere en el rango de la otra. En la gráfica de líneas de Tabla\(\PageIndex{2}\), por ejemplo, cada punto representa el tiempo medio de respuesta para los participantes con apellidos en el primer, segundo, tercero y cuarto cuartiles (o trimestres) de la distribución de nombres. Muestra claramente cómo el tiempo de respuesta tiende a disminuir a medida que los apellidos de las personas se acercan al final del alfabeto. La gráfica de dispersión en Table\(\PageIndex{3}\), muestra la relación entre 25 métodos de investigación de los resultados de los estudiantes en la Escala de Autoestima de Rosenberg dadas en dos ocasiones a la semana de diferencia. Aquí los puntos representan a individuos, y podemos ver que a mayor puntuación de alumnos en la primera ocasión, mayor tendieron a anotar en la segunda ocasión. En general, los gráficos de líneas se utilizan cuando la variable en el eje x tiene (o está organizada en) un pequeño número de valores distintos, como los cuatro cuartiles de la distribución de nombres. Los diagramas de dispersión se utilizan cuando la variable en el eje x tiene un gran número de valores, como las diferentes puntuaciones posibles de autoestima.

Tabla\(\PageIndex{3}\): Relación estadística entre las puntuaciones de varios estudiantes universitarios en la escala de autoestima de Rosenberg dadas en dos ocasiones a la semana de diferencia

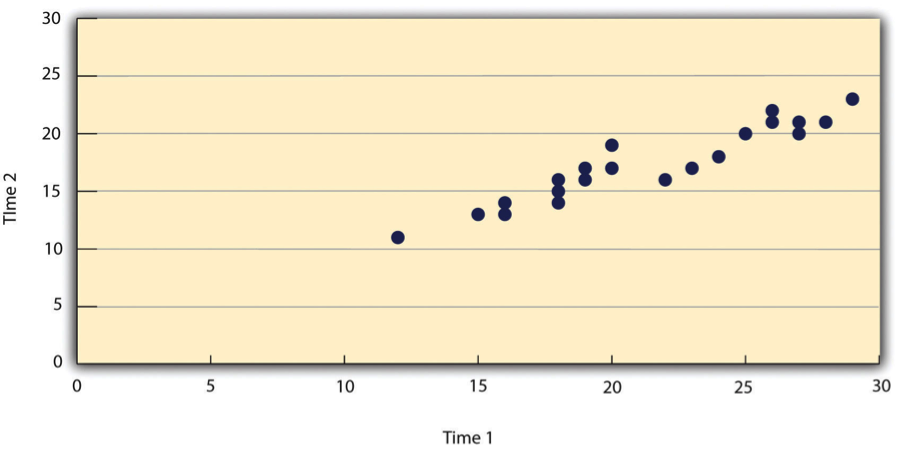
Los datos presentados en la Tabla\(\PageIndex{3}\) proporcionan un buen ejemplo de una relación positiva, en la que las puntuaciones más altas en una variable tienden a asociarse con puntuaciones más altas en la otra (de manera que los puntos van de la parte inferior izquierda a la parte superior derecha de la gráfica). Los datos presentados en la Tabla\(\PageIndex{2}\) proporcionan un buen ejemplo de una relación negativa, en la que las puntuaciones más altas en una variable tienden a asociarse con puntuaciones más bajas en la otra (de manera que los puntos van de la parte superior izquierda a la inferior derecha).

Ambos ejemplos son también relaciones lineales, en las que los puntos se ajustan razonablemente bien por una sola línea recta. Las relaciones no lineales son aquellas en las que los puntos se ajustan mejor por una línea curva. La tabla\(\PageIndex{4}\), por ejemplo, muestra una relación hipotética entre la cantidad de sueño que las personas duermen por noche y su nivel de depresión. En este ejemplo, la línea que mejor se ajusta a los puntos es una curva —una especie de “U” al revés— porque las personas que duermen unas ocho horas tienden a ser las menos deprimidas, mientras que las que duermen muy poco y las que duermen demasiado tienden a estar más deprimidas. Las relaciones no lineales no son infrecuentes en psicología, pero una discusión detallada de ellas está más allá del alcance de este libro.

Tabla\(\PageIndex{4}\): Una relación hipotética no lineal entre cuánto duermen las personas por noche y qué tan deprimidas están

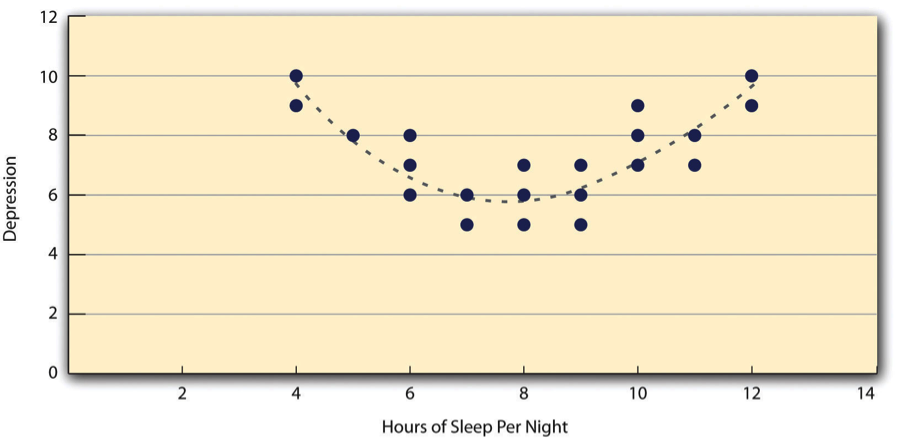
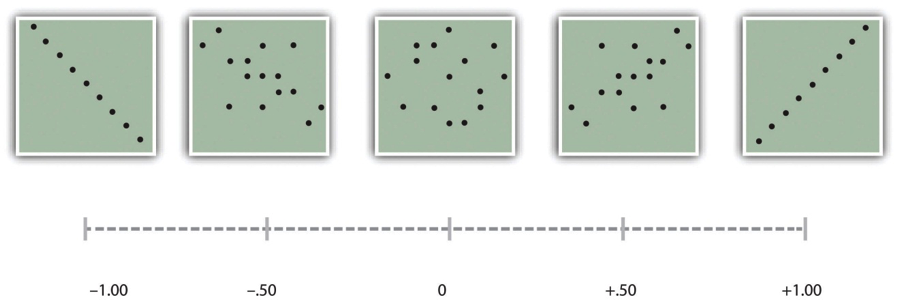
Como vimos anteriormente en el libro, la fuerza de una correlación entre variables cuantitativas se mide típicamente usando una estadística llamada r de Pearson. Como\(\PageIndex{5}\) muestra la Tabla, sus posibles valores oscilan entre −1.00, pasando por cero, hasta +1.00. Un valor de 0 significa que no hay relación entre las dos variables. Además de sus pautas para interpretar la d de Cohen, Cohen ofreció pautas para interpretar la r de Pearson en la investigación psicológica (ver Tabla\(\PageIndex{1}\)). Los valores cercanos a ±.10 se consideran pequeños, los valores cercanos a ± .30 se consideran medianos y los valores cercanos a ±.50 se consideran grandes. Observe que el signo de la r de Pearson no está relacionado con su fuerza. Los valores r de Pearson de +.30 y −.30, por ejemplo, son igualmente fuertes; es solo que uno representa una relación positiva moderada y el otro una relación negativa moderada. Al igual que la d de Cohen, la r de Pearson también se conoce como una medida del “tamaño del efecto” a pesar de que la relación puede no ser causal.

Tabla\(\PageIndex{5}\): La r de Pearson oscila entre −1.00 (que representa la relación negativa más fuerte posible), pasando por 0 (que representa la ausencia de relación), hasta +1.00 (representando la relación positiva más fuerte posible)

Los cálculos para r de Pearson son más complicados que los de la d de Cohen. Aunque quizás nunca tengas que hacerlas a mano, sigue siendo instructivo ver cómo. Computacionalmente, la r de Pearson es el “producto cruzado medio de las puntuaciones z”. Para calcularlo, uno comienza transformando todos los puntajes en puntuaciones z. Para la variable X, reste la media de X de cada puntaje y divida cada diferencia por la desviación estándar de X. Para la variable Y, reste la media de Y de cada puntaje y divida cada diferencia por la desviación estándar de Y. Luego, para cada individuo, multiplique las dos puntuaciones z juntas para formar un producto cruzado. Por último, tomar la media de los productos cruzados. La fórmula se ve así:

\[r=\frac{\sum\left(z_{x} z_{y}\right)}{N}\]

\(\PageIndex{2}\)La tabla ilustra estos cálculos para un pequeño conjunto de datos. La primera columna enumera las puntuaciones para la variable X, que tiene una media de 4.00 y una desviación estándar de 1.90. La segunda columna es la puntuación z- para cada uno de estos puntajes brutos. En las columnas tercera y cuarta se enumeran los puntajes brutos para la variable Y, que tiene una media de 40 y una desviación estándar de 11.78, y las puntuaciones z correspondientes. En la quinta columna se enumeran los productos cruzados. Por ejemplo, el primero es 0.00 multiplicado por −0.85, que es igual a 0.00. El segundo es 1.58 multiplicado por 1.19, que es igual a 1.88. La media de estos productos cruzados, que se muestra en la parte inferior de esa columna, es r de Pearson, que en este caso es +.53. Hay otras fórmulas para computar el r de Pearson a mano que pueden ser más rápidas. Este enfoque, sin embargo, es mucho más claro en términos de comunicar conceptualmente cuál es la r de Pearson.

Tabla\(\PageIndex{2}\): Cálculos de muestra para r de Pearson

X	z x	Y	z y	z x z
4	0.00	30	−0.85	0.00
7	1.58	54	1.19	1.88
2	−1.05	23	−1.44	1.52
5	0.53	43	0.26	0.13
2	−1.05	50	0.85	−0.89
M x = 4.00		M y = 40.00		r = 0.53
SD x = 1.90		SD y = 11.78

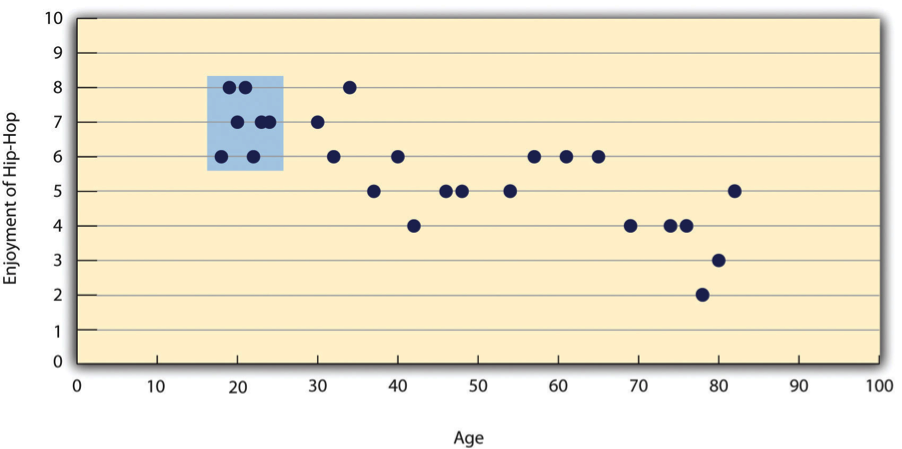
Como vimos antes, hay dos situaciones comunes en las que el valor de r de Pearson puede ser engañoso. Una es cuando la relación en estudio es no lineal. A pesar de que Table\(\PageIndex{4}\) muestra una relación bastante fuerte entre la depresión y el sueño, la r de Pearson estaría cerca de cero porque los puntos en la gráfica de dispersión no están bien ajustados por una sola línea recta. Esto significa que es importante hacer una gráfica de dispersión y confirmar que una relación es aproximadamente lineal antes de usar r de Pearson. La otra es cuando una o ambas variables tienen un rango limitado en la muestra en relación con la población. Este problema se conoce como restricción de rango. Supongamos, por ejemplo, que existe una fuerte correlación negativa entre la edad de las personas y su disfrute de la música hip hop como lo muestra la trama de dispersión en Table\(\PageIndex{6}\). La r de Pearson aquí es −.77. Sin embargo, si tuviéramos que recolectar datos solo de 18 a 24 años de edad, representados por el área sombreada de\(\PageIndex{7}\) Table, entonces la relación parecería ser bastante débil. De hecho, la r de Pearson para este rango restringido de edades es 0. Es una buena idea, por lo tanto, diseñar estudios para evitar la restricción de rango. Por ejemplo, si la edad es una de tus variables principales, entonces puedes planear recopilar datos de personas de un amplio rango de edades. Debido a que la restricción de rango no siempre se anticipa o se puede evitar fácilmente, sin embargo, es una buena práctica examinar sus datos en busca de una posible restricción de rango e interpretar la r de Pearson a la luz de ella. (También existen métodos estadísticos para corregir la r de Pearson para la restricción de rango, pero están más allá del alcance de este libro).

Tabla\(\PageIndex{6}\): Datos hipotéticos que muestran cómo una correlación general fuerte puede parecer débil cuando una variable tiene un rango restringido. La correlación general aquí es −.77, pero la correlación para los jóvenes de 18 a 24 años (en el cuadro azul) es 0.

Referencias

1. Ollendick, T. H., Öst, L.-G., Reuterskiöld, L., Costa, N., Cederlund, R., Sirbu, C.,... Jarrett, M. A. (2009). Tratamientos de una sesión de fobias específicas en jóvenes: Un ensayo clínico aleatorizado en Estados Unidos y Suecia. Revista de Consultoría y Psicología Clínica, 77, 504—516.
2. Cohen, J. (1992). Una imprimación de potencia. Boletín Psicológico, 112, 155—159.
3. Hyde, J. S. (2007). Nuevas direcciones en el estudio de las similitudes y diferencias de género. Direcciones Actuales en Ciencia Psicológica, 16, 259—263.
4. Carlson, K. A., & Conard, J. M. (2011). El efecto apellido: Cómo influye el apellido en el tiempo de adquisición. Revista de Investigación del Consumidor, 38 (2), 300-307. doi: 10.1086/658470