2.3: De las leyes del pensamiento a la lógica binaria

En 1854, con la publicación de Una investigación de las leyes del pensamiento, George Boole (2003) inventó la lógica matemática moderna. El objetivo de Boole era trasladar el estudio del pensamiento del dominio de la filosofía al dominio de las matemáticas:

No sólo existe una estrecha analogía entre las operaciones de la mente en el razonamiento general y sus operaciones en la ciencia particular del Álgebra, sino que existe en gran medida un acuerdo exacto en las leyes por el cual se llevan a cabo las dos clases de operaciones. (Boole, 2003, p. 6)

Hoy asociamos el nombre de Boole con la lógica subyacente a las computadoras digitales (Mendelson, 1970). Sin embargo, el álgebra de Boole tiene poco parecido con nuestra interpretación moderna de la misma. El propósito de esta sección es trazar la trayectoria que nos lleva desde el cálculo decimonónico de Boole hasta la invención del siglo XX de tablas de verdad que definen funciones lógicas sobre dos entradas binarias.

Boole no creó una lógica binaria; en cambio desarrolló un álgebra de conjuntos. Boole utilizó símbolos como\(x,\,y,\) y\(z\) para representar clases de entidades. Luego definió “signos de operación, como +, —, ', que representan aquellas operaciones de la mente mediante las cuales se combinan o resuelven las concepciones de las cosas para formar nuevas concepciones que involucran los mismos elementos” (Boole, 2003, p. 27). Las operaciones de su álgebra fueron las de elección: seleccionaron subconjuntos de entidades de diversas clases de interés (Lewis, 1918).

Por ejemplo, considere dos clases:\(x\) (ej., “cosas negras”) y\(y\) (por ejemplo, “pájaros”). La expresión de Boole\(x\,+\,y\) realiza una “exclusiva o” de las dos clases constituyentes, eligiendo las entidades que eran “cosas negras”, o eran “pájaros”, pero no las que eran “pájaros negros”.

Elementos del álgebra de Boole apuntaban en la dirección de nuestra lógica binaria más moderna. Por ejemplo, Boole utilizó la multiplicación para elegir entidades que compartían propiedades definidas por clases separadas. Entonces, continuando con nuestro ejemplo, el conjunto de “pájaros negros” sería elegido por la expresión\(xy\). Boole también reconoció que si uno multiplicaba una clase consigo mismo, el resultado simplemente sería el conjunto original nuevamente. Boole escribió su ley fundamental del pensamiento como\(xx\,=\,x\), que también se puede expresar como\(x^2\,=\,x\). Se dio cuenta de que si se asignaban cantidades numéricas a\(x\), entonces esta ley sólo sería cierta para los valores 0 y 1. “Así es consecuencia de que la ecuación fundamental del pensamiento es de segundo grado, que realizamos la operación de análisis y clasificación, por división en pares de opuestos, o, como se dice técnicamente, por dicotomía” (Boole, 2003, pp. 50—51). Aún así, esta dicotomía no debía interpretarse exclusivamente en términos de verdad o falsedad, aunque Boole explotó esta representación en su tratamiento de proposiciones secundarias. Boole solía utilizar 0 para representar el conjunto vacío y 1 para representar el conjunto universal; la expresión\(1\,–\,x\) eligió aquellas entidades a las que no pertenecían\(x\).

Las operaciones de Boole sobre símbolos fueron puramente formales. Es decir, las acciones de sus reglas lógicas eran independientes de cualquier interpretación semántica de los términos lógicos que se manipulaban.

De hecho, podemos dejar de lado la interpretación lógica de los símbolos en la ecuación dada; convertirlos en símbolos cuantitativos, susceptibles solo de los valores 0 y 1; realizar sobre ellos como tales todos los procesos de solución necesarios; y finalmente restaurarles su lógica interpretación. (Boole, 2003, p. 70)

Este enfoque formal es evidente en el análisis de Boole de su ley fundamental. Comenzando con\(x^2\,=\,x\), Boole aplicó álgebra básica para convertir esta expresión en\(x\,–\,x^2\,=\,0\). Luego simplificó esta expresión a\(x(1\,–\,x)\,=\,0\). Tenga en cuenta que ninguno de estos pasos es de naturaleza lógica; Boole no podría proporcionar una justificación lógica para su derivación. No obstante, sí brindó triunfalmente una interpretación lógica de su resultado: 0 es el conjunto vacío, 1 el conjunto universal,\(x\) es algún conjunto de interés, y\(1\,–\,x\) es la negación de este conjunto. La derivación algebraica de Boole muestra así que la intersección de\(x\) con su negación es el conjunto vacío. Boole señaló que, en términos de lógica, la ecuación\(x(1\,–\,x)\,=\,0\) expresa,

que es imposible que un ser posea una cualidad y no posea esa cualidad al mismo tiempo. Pero esto es idénticamente ese 'principio de contradicción' que Aristóteles ha descrito como el axioma fundamental de toda filosofía. (Boole, 2003, p. 49)

Era importante para Boole vincular su cálculo a Aristóteles, porque Boole no sólo tenía en alta estima la lógica aristotélica, sino que también esperaba que sus nuevos métodos matemáticos apoyaran tanto los logros lógicos clave de Aristóteles como extendieran la obra de Aristóteles en nuevas direcciones. Para vincular aún más su formalismo a la lógica de Aristóteles, Boole aplicó sus métodos a lo que llamó proposiciones secundarias. Una proposición secundaria era una declaración sobre una proposición que podía ser verdadera o falsa. Como resultado, el análisis de Boole de las proposiciones secundarias proporciona otro atisbo de cómo su obra se relaciona con nuestra interpretación binaria moderna de la misma.

Boole aplicó su álgebra de conjuntos a proposiciones secundarias adoptando una interpretación temporal de la elección. Es decir, Boole consideró que una proposición secundaria podría ser verdadera o falsa por algún tiempo de interés. La expresión ahora se\(xy\) interpretaría como la elección de un periodo temporal durante el cual ambas proposiciones\(x\) y\(y\) son verdaderas. A los símbolos 0 y 1 también se les dieron interpretaciones temporales, lo que significa “no tiempo” y “todo el tiempo” respectivamente. Si bien este uso difiere sustancialmente de nuestro enfoque moderno, ha sido visto como la inspiración para la lógica binaria moderna (Post, 1921).

El trabajo de Boole inspiró el trabajo posterior sobre la lógica de dos maneras diferentes. Primero, Boole demostró que un álgebra de símbolos era posible, productivo y digno de exploración: “Boole demostró indiscutiblemente que era posible, con la ayuda de un sistema de signos matemáticos, deducir las conclusiones de todos estos modos antiguos de razonamiento, y un número indefinido de otras conclusiones ” (Jevons, 1870, p. 499). En segundo lugar, los logísticos notaron ciertas idiosincrasias y deficiencias con el cálculo de Boole, y trabajaron en tratar estos problemas. Jevons también escribió que los ejemplos de Boole “solo pueden ser seguidos por mentes matemáticas altamente logradas; e incluso un matemático no encontraría ninguna fuerza demostrativa en un cálculo que emplea sin miedo símbolos inintencionales e incomprensibles” (p. 499). Los intentos de simplificar y corregir Boole produjeron nuevos sistemas lógicos que sirven de puente entre la lógica del siglo XIX de Boole y la lógica binaria que surgió en el siglo XX.

La lógica de Boole es problemática porque ciertas operaciones matemáticas no tienen sentido dentro de ella (Jevons, 1870). Por ejemplo, debido a que la adición definía el “exclusivo o” de dos conjuntos, la expresión no\(x\,+\,x\) tenía interpretación en el sistema de Boole. Jevons creía que la interpretación de la adición de Boole estaba profundamente equivocada y corrigió esto definiendo la adición como la “inclusiva o” de dos series. Esto produjo una ley aditiva interpretable,\(x\,+\,x\,=\,x\), que era paralela a la ley fundamental multiplicativa del pensamiento de Boole.

La revisión de Jevons (1870) del álgebra de Boole condujo a un sistema que era lo suficientemente simple como para permitir la inferencia lógica para ser mecanizada. Jevons ilustró esto con un sistema de tres clases, en el que las letras mayúsculas (e.g.,\(A\)) seleccionaban aquellas entidades que pertenecían a un conjunto y las letras minúsculas (por ejemplo,\(a\)) seleccionaban aquellas entidades que no pertenecían. Posteriormente produjo lo que llamó el abecedario lógico, que era el conjunto de posibles combinaciones de las tres clases. En su ejemplo de tres clases, el abecedario constaba de ocho combinaciones:\(ABC,\,ABc,\,AbC,\,Abc,\,aBC,\,aBc,\,abC,\) y\(abc\). Tenga en cuenta que cada una de estas combinaciones es una multiplicación de tres términos en el sentido de Boole, y así elige una intersección de tres clases diferentes. Además, con la definición mejorada de adición lógica, se podrían sumar diferentes términos del abecedario para definir algún conjunto de interés. Por ejemplo Jevons (¡pero no Boole!) podría elegir la clase\(B\) con la siguiente expresión:\(B\,=\,ABC\,+\,ABc\,+\,aBC\,+\,aBc\).

Jevons (1870) demostró cómo el abecedario podría ser utilizado como motor de inferencia. Primero, utilizó su notación set para definir conceptos de interés, como en el ejemplo\(A\) = hierro,\(B\) = metal, y\(C\) = elemento. Segundo, tradujo proposiciones en intersecciones de conjuntos. Por ejemplo, la premisa “El hierro es metal” se puede reescribir como “\(A\)es”\(B\), que en el álgebra de Boole se convierte\(AB\), y “el metal es elemento” se convierte\(BC\). Tercero, dado un conjunto de premisas, Jevons eliminó del abecedario los términos que eran inconsistentes con los locales: los únicos términos congruentes con los locales\(AB\) y\(BC\) son\(ABC,\,aBC,\,abC,\) y\(abc\). Cuarto, Jevons inspeccionó e interpretó los términos de abecedario restantes para realizar inferencias lógicas válidas. Por ejemplo, de los cuatro términos restantes en el ejemplo de Jevons, podemos concluir que “todo el hierro es elemento”, porque sólo\(A\) se empareja con\(C\) los términos que quedan, y “hay algunos elementos que no son ni metal ni hierro”, o\(abC\). Por supuesto, el conjunto completo de entidades que es electo por las premisas es la suma lógica de los términos que no fueron eliminados.

Jevons (1870) creó un dispositivo mecánico para automatizar el procedimiento descrito anteriormente. La máquina, conocida como el “piano lógico” por su apariencia, mostró las 16 combinaciones diferentes del abecedario para trabajar con cuatro clases diferentes. Los locales se ingresaron presionando las teclas; la depresión de un patrón de teclas eliminó términos inconsistentes de abecedario de la vista. Después de que todas las premisas se hubieran ingresado en secuencia, se interpretaron los términos que permanecieron en exhibición. Allan Marquand (Marquand, 1885) inventó una variación más simple del dispositivo de Jevons, originalmente desarrollado para problemas de cuatro clases pero más fácilmente extensible a situaciones más grandes. Marquand posteriormente produjo planos para una versión eléctrica de su dispositivo que utilizaba electroimanes para controlar la pantalla (Mays, 1953). Si se hubiera construido este dispositivo y si el trabajo de Marquand hubiera llamado la atención de un público más amplio, la computadora digital podría haber sido un invento del siglo XIX (Buck & Hunka, 1999).

Con respecto a nuestro interés en la transición de la obra de Boole a nuestra interpretación moderna de la misma, tenga en cuenta que los sistemas lógicos desarrollados por Jevons, Marquand y otros eran binarios en dos sentidos diferentes. Primero, un conjunto y su complemento (e.g.,\(A\) y\(a\)) nunca coocurrieron en el mismo término abecedario. Segundo, cuando se aplicaron premisas, se eliminó o no un término de abecedario. Estas características binarias de tales sistemas les permitieron ser lo suficientemente simples como para ser mecanizados.

El siguiente paso hacia la lógica binaria moderna fue adoptar la práctica de asumir que las proposiciones podían ser verdaderas o falsas, e indicar algebraicamente estos estados con los valores 1 y 0. Hemos visto que Boole inició este enfoque, pero que lo hizo aplicando incómodas interpretaciones teóricas de conjuntos temporales a estos dos símbolos.

El uso moderno del 1 y el 0 para representar lo verdadero y lo falso surge más adelante en el siglo XIX. La lógica simbólica del lógico británico Hugh McColl (1880) utilizó esta notación, que tomó prestada de las matemáticas de la probabilidad. El lógico estadounidense Charles Sanders Peirce (1885) también utilizó explícitamente una notación binaria para la verdad en su famoso artículo “Sobre el álgebra de la lógica: Una contribución a la filosofía de la notación”. A menudo se cita este artículo como el que introdujo el uso moderno (Ewald, 1996). Peirce extendió el trabajo de Boole sobre proposiciones secundarias al estipular una ley algebraica adicional de proposiciones: para cada elemento\(x\), ya sea\(x\,=\,0\) o\(x\,=\,1\), produciendo un sistema conocido como “el álgebra de dos valores” (Lewis, 1918).

El álgebra de dos valores condujo a la invención de tablas de la verdad, que se establecen en la literatura a principios de los años 20 (Post, 1921; Wittgenstein, 1922), pero probablemente estaban en uso mucho antes. Hay evidencia de que Bertrand Russell y su entonces alumno Ludwig Wittgenstein estaban usando tablas de la verdad ya en 1910 (Shosky, 1997). También se ha argumentado que Charles Peirce y sus alumnos probablemente estaban usando tablas de la verdad ya en 1902 (Anellis, 2004).

Las tablas de verdad hacen explícito un enfoque en el que se utilizan proposiciones primitivas (\(p,\,q,\,r,\)etc.) que sólo podrían adoptar valores de 0 o 1 para producir expresiones más complejas. Estas expresiones se producen mediante el uso de funciones lógicas para combinar términos más simples. Este enfoque se conoce como “usando sistemas de verdad-valor” (Lewis y Langford, 1959). Los sistemas de verdad-valor utilizan esencialmente tablas de verdad para determinar la verdad de funciones de proposiciones (es decir, de combinaciones lógicas de proposiciones). “Es una característica distintiva de este sistema de dos valores que cuando se da la propiedad, 0 ó 1, de los elementos\(p,\,q,\) etc., se determina con ello que cualquier función de los elementos que se encuentra en el sistema tiene la propiedad 0 o la propiedad 1” (p. 199).

Considerar Tabla\(PageIndex{1}\), que proporciona los valores de tres funciones diferentes (las últimas tres columnas de la tabla) dependiendo del valor de verdad de dos proposiciones simples (las dos primeras columnas de la tabla):

\(p\)	\(q\)	\(p\cdot q\)	\(p+q\)	\(p\cdot (p+q)\)
1	1	1	1	1
1	0	0	1	1
0	1	0	1	0
0	0	0	0	0

Cuadro 1. Ejemplos del sistema de valores de la verdad para dos proposiciones elementales y algunas de sus combinaciones. Los posibles valores de p y q se dan en las dos primeras columnas. Los valores resultantes de las diferentes funciones de estas proposiciones se proporcionan en las columnas restantes.

Los sistemas de verdad-valor dan como resultado un enfoque sorprendente y simplificado para definir funciones lógicas básicas o primitivas. Cuando las proposiciones p y q se interpretan como que son solo verdaderas o falsas, entonces solo hay cuatro combinaciones posibles de estas dos proposiciones que pueden existir, es decir, las dos primeras columnas de Table\(PageIndex{1}\). Una función primitiva se puede definir como una función que se define sobre p y q, y que adquiere un valor de verdad para cada combinación de estas variables.

Dado que en un sistema de verdad-valor una función sólo puede tomar el valor de 0 o 1, entonces sólo hay 16 funciones primitivas diferentes que pueden definirse para combinaciones de las entradas binarias p y q (Ladd, 1883). Estas funciones primitivas se proporcionan en Tabla\(PageIndex{2}\); cada fila de la tabla muestra los valores de verdad de cada función para cada combinación de las entradas. Un ejemplo de notación lógica para cada función se proporciona en la última columna de la tabla. Esta notación fue utilizada por Warren McCulloch (1988b), quien la atribuyó a trabajos anteriores de Wittgenstein.

No es sorprendente que también se pueda trazar una trayectoria histórica para la lógica binaria definida en Table\(PageIndex{2}\). La alumna de Peirce, Christine Ladd, produjo en realidad las primeras cinco columnas de esa tabla en su artículo de 1883, incluida la conversión de los primeros cuatro números seguidos de un número binario a un número base 10. Sin embargo, Ladd no interpretó cada fila como definiendo una función lógica. En cambio, vio las columnas en términos de notación fija y cada fila definía un “universo” diferente. La interpretación de las primeras cuatro columnas como los valores de verdad de diversas funciones lógicas surgió posteriormente con la popularización de las tablas de verdad (Post, 1921; Wittgenstein, 1922).

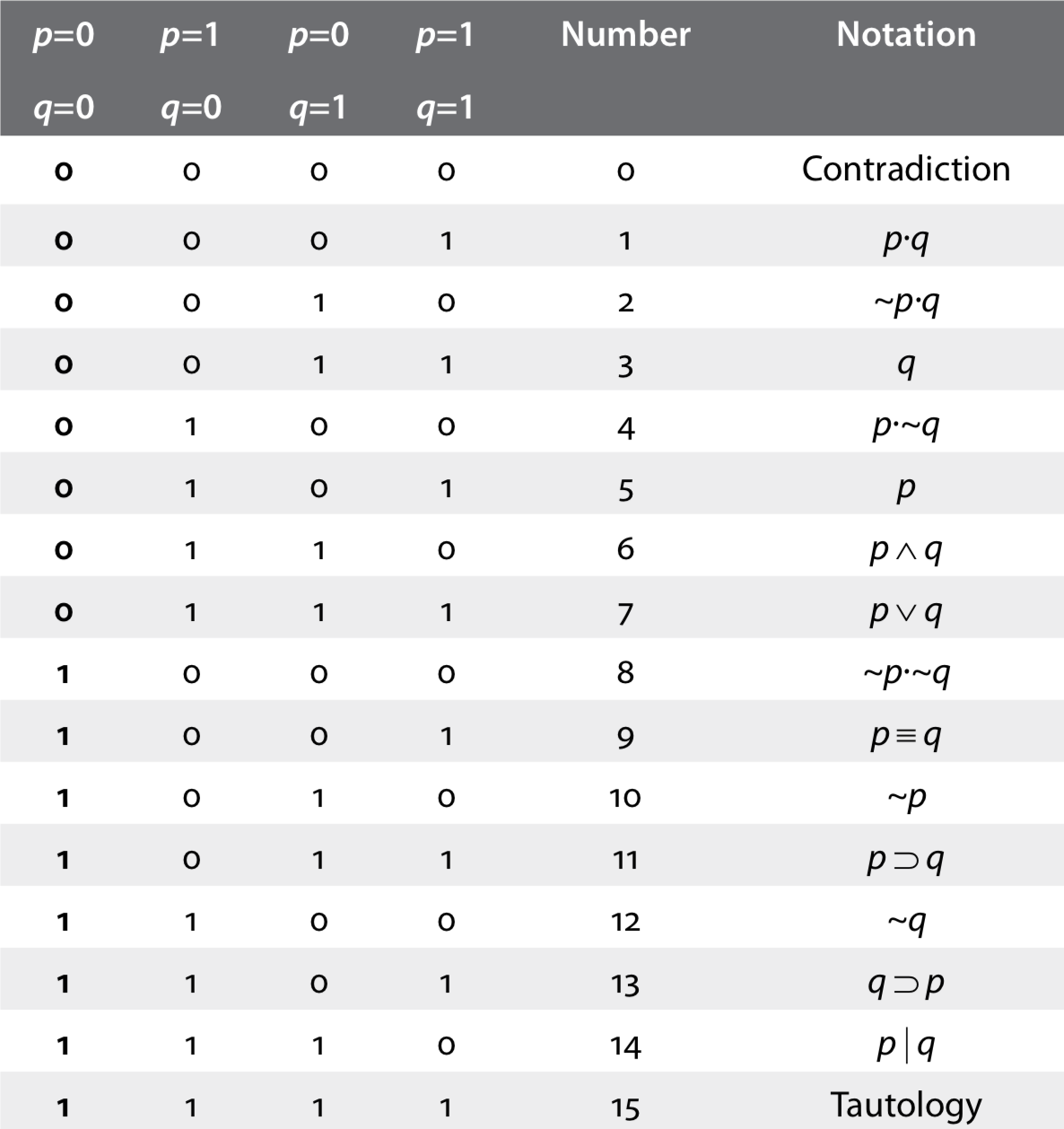
Cuadro 2. Tablas de verdad para todas las funciones posibles de pares de proposiciones. Cada función tiene un valor de verdad por cada combinación posible de los valores de verdad de p y q, dados en las primeras cuatro columnas de la tabla. La columna Número convierte los primeros cuatro valores de una fila en un número binario (Ladd, 1883). La notación lógica para cada función se toma Warren McCulloch (1988b).

Las tablas de la verdad, y el sistema de verdad-valor que apoyan, son muy poderosas. Se pueden utilizar para determinar si alguna expresión compleja, basada en combinaciones de proposiciones primitivas y operaciones lógicas primitivas, es verdadera o falsa (Lewis, 1932). En la siguiente sección vemos el poder del sistema binario simple de verdad-valor, porque es la base de la computadora digital moderna. También vemos que dar vida a este sistema en una computadora digital lleva a la conclusión de que se debe usar más de un vocabulario para explicar los dispositivos lógicos.