3.3: Mecanizar el Infinito

Hemos visto que la mente cartesiana incorpórea es la cosa pensante que media en la percepción del mundo y que actúa sobre él. Lo hace participando en actividades tales como dudar, comprender, afirmar, negar, percibir, imaginar y querer. Estas actividades fueron consideradas por Descartes como análogas al uso de reglas por parte de un geómetro para manipular expresiones matemáticas. Esto nos lleva a preguntarnos, ¿en qué medio se lleva a cabo el pensamiento? ¿Qué reglas formales emplea? ¿Qué expresiones simbólicas manipula?

Muchos otros filósofos simpatizaron con la afirmación de que la actividad mental era una especie de manipulación de símbolos. Thomas Hobbes es reclamado como uno de los padres filosóficos de la ciencia cognitiva clásica debido a sus escritos sobre la naturaleza de la mente:

Cuando un hombre Razoneth, ji no hace otra cosa que concebir un summe totall, de Adición de parcelas; o concebir un Resto, de Sustracción de un summe de otro”. Tales operaciones no se limitaban a números: “Estas operaciones no son incidentes solo a Números, sino a todo tipo de cosas que pueden sumarse, y sacarse una de otra. (Hobbes, 1967, p. 32)

Hobbes señaló que los geometristas aplicaron tales operaciones a líneas y figuras, y que los logísticos aplicaron estas operaciones a las palabras. Por lo tanto, no es sorprendente que Hobbes describiera el pensamiento como un discurso mental—pensar, para él, era parecido al lenguaje.

¿Por qué a los estudiosos les tomó la idea de que el lenguaje era el medio en el que se conducía el pensamiento Primero, coincidieron en que el pensamiento era excepcionalmente poderoso, en el sentido de que no había límites para la creación de ideas. En otras palabras, el hombre en principio era capaz de una infinita variedad de pensamientos diferentes. “La razón es un instrumento universal que puede operar en todo tipo de situaciones” (Descartes, 2006, p. 47). Segundo, el lenguaje era un medio en el que se podía expresar el pensamiento, porque también era capaz de una variedad infinita. Descartes expresó esto de la siguiente manera:

Porque es un hecho muy notable que no haya hombres tan tontos y estúpidos, ni siquiera locos, que sean incapaces de encadenar diferentes palabras, y componerlas en enunciados, a través de los cuales dejan conocer sus pensamientos. (Descartes, 2006, p. 47) Los lingüistas modernos describen esto como el aspecto creativo del lenguaje (Chomsky, 1965, 1966). “Una propiedad esencial del lenguaje es que proporciona los medios para expresar indefinidamente muchos pensamientos y para reaccionar adecuadamente en un rango indefinido de nuevas situaciones” (Chomsky, 1965, p. 6).

Si bien Descartes no escribió mucho sobre el lenguaje específicamente (Chomsky, 1966), es claro que simpatizaba con la noción de que el lenguaje era el medio para el pensamiento. Esto se debe a que utilizó el aspecto creativo del lenguaje para argumentar a favor del dualismo. Inspirado en los autómatas que aparecían en Europa en su época, Descartes imaginó la posibilidad de tener que demostrar que los sofisticados dispositivos futuros no eran humanos. Anticipó la prueba de Turing (Turing, 1950) por más de tres siglos utilizando el lenguaje para separar al hombre de la máquina.

Porque bien podemos concebir una máquina hecha de tal manera que emita palabras, e incluso las pronuncia sobre acciones corporales que provocan algún cambio correspondiente en sus órganos.. pero no es concebible que ponga estas palabras en diferentes órdenes para que correspondan al sentido de las cosas dichas en su presencia. (Descartes, 2006, p. 46)

Siglos después, argumentos similares siguen apareciendo en la filosofía. Por ejemplo, ¿por qué una grabación fonográfica de toda la vida del habla de alguien es una simulación inadecuada de ese discurso (Fodor, 1968b)? “En el mejor de los casos, los fonógrafos hacen lo que hacen los hablantes, no lo que pueden hacer los hablantes” (p. 129).

¿Por qué podría ser imposible que un dispositivo haga lo que los altavoces pueden hacer? Para Descartes, las máquinas productoras de lenguaje eran inconcebibles porque las máquinas eran físicas y por lo tanto finitas. Su naturaleza finita les impidió ser infinitamente variables.

Aunque tales máquinas podrían hacer muchas cosas tan bien o incluso mejor que cualquiera de nosotros, inevitablemente dejarían de hacer algunas otras, por lo que descubriríamos que no actuaban conscientemente, sino sólo porque sus órganos estaban dispuestos de cierta manera. (Descartes, 2006, pp. 46—47)

En otras palabras, la creatividad del pensamiento o del lenguaje sólo era posible en la mente infinita, no física, incorpórea.

Es esta conclusión de Descartes la que lleva a una marcada distinción entre la filosofía cartesiana y la ciencia cognitiva clásica. La ciencia cognitiva clásica abarca el aspecto creativo del lenguaje. Sin embargo, ve tal creatividad desde una perspectiva materialista, no dualista. Los desarrollos en la lógica y en la computación ocurridos desde el siglo XVII han producido un dispositivo que Descartes no tenía a su disposición: el sistema de símbolos físicos. Y, aparentemente mágicamente, un sistema de símbolos físicos es un artefacto finito que es capaz de una variedad infinita de comportamientos.

Para el siglo XIX, la noción del lenguaje como sistema finito que podría ser infinitamente expresivo estaba bien establecida (Humboldt, 1999, p. 91): “Porque el lenguaje se enfrenta de manera bastante peculiar a un dominio interminable y verdaderamente ilimitado, la esencia de todo lo que se puede pensar. Por lo tanto, debe hacer un empleo infinito de medios finitos”. Si bien se ha argumentado que la teoría del lenguaje de Humboldt presagiaba muchas de las propiedades clave de las gramáticas generativas modernas (Chomsky, 1966), no logró dar una respuesta específica a la pregunta fundacional que planteó: ¿cómo puede un sistema finito producir lo infinito? La respuesta a esa pregunta requirió avances en la lógica y las matemáticas que vinieron después de Humboldt, y que a su vez fueron posteriormente traídos a la vida por las computadoras digitales.

Si bien desde hace siglos se sospechaba que todas las matemáticas puras tradicionales pueden derivarse de las propiedades básicas de los números naturales, la confirmación de esta sospecha sólo se obtuvo con avances ocurridos en los siglos XIX y XX (Russell, 1993). La “aritmetización” de las matemáticas se estableció en el siglo XIX, en lo que se llaman los axiomas Dedekind-Peano (Dedekind, 1901; Peano, 1973). Esta teoría matemática define tres nociones primitivas: 0, número y sucesor. También define cinco proposiciones básicas: 0 es un número; el sucesor de cualquier número es un número; no hay dos números que tengan el mismo sucesor; 0 no es el sucesor de ningún número; y el principio de inducción matemática. Estas ideas básicas fueron suficientes para generar toda la teoría de los números naturales (Russell, 1993).

De particular interés para nosotros es el procedimiento que se utiliza en este sistema para generar el conjunto de números naturales. El conjunto comienza con 0. El siguiente número es 1, que puede definirse como el sucesor de 0, como s (0). El siguiente número es 2, que es el sucesor de 1, s (1), y también es el sucesor del sucesor de 0, s (s (0)). En otras palabras, la función sucesora se puede utilizar para crear el conjunto completo de números naturales: 0, s (0), s (s (0)), s (s (s (0))), y así sucesivamente.

La definición de números naturales usando la función sucesora es un ejemplo de recursión simple; una función es recursiva cuando opera refiriéndose a sí misma. La expresión s (s (0)) es recursiva porque la primera función sucesora toma como entrada otra versión de sí misma. La recursión es un método por el cual un sistema finito (como los axiomas Dedekind-Peano) puede producir variedad infinita, como en el conjunto de números naturales.

La recursión no se limita al mundo abstracto de las matemáticas, ni su único papel es generar variedad infinita. Puede funcionar en sentido contrario, transformando lo grande y complejo en lo pequeño y simple. Por ejemplo, la recursión puede ser utilizada para resolver un problema complejo reduciéndolo a una versión simple de sí misma. Este enfoque de resolución de problemas a menudo se llama dividir y conquistar (Knuth, 1997).

Un ejemplo de ello es el famoso problema de la Torre de Hanoi (ver Figura 3-1), presentado por primera vez al mundo como un rompecabezas de madera por el matemático francés Edouard Lucas en 1883. En este rompecabezas, hay tres ubicaciones, A, B y C. Al inicio de este problema hay un conjunto de discos de madera de diferentes tamaños apilados uno sobre otro en la ubicación A. Vamos a numerar estos discos 0, 1, 2, y así sucesivamente, donde el número asignado a un disco indica su tamaño. El objetivo del problema es mover toda esta pila a la ubicación C, bajo dos restricciones: primero, solo se puede mover un disco a la vez; segundo, un disco más grande nunca se puede colocar sobre un disco más pequeño.

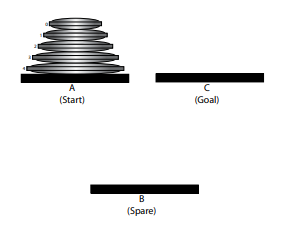
Figura 3-1. La configuración inicial para una versión de cinco discos del problema de la Torre de Hanoi.

La versión más simple del problema de la Torre de Hanoi comienza con solo el disco 0 en la ubicación A. Su solución es completamente sencilla: el disco 0 se mueve directamente a la ubicación C, y el problema está resuelto. El problema solo es un poco más complicado si comienza con dos discos apilados en la ubicación A. Primero, el disco 0 se mueve a la ubicación B. Segundo, el disco 1 se mueve a la ubicación C. Tercero, el disco 0 se mueve de A a C, se apila encima del disco 1, y el problema se ha resuelto.

¿Y un problema de la Torre de Hanoi que comienza con tres discos? Para resolver este problema más complicado, primero podemos definir un subproblema más simple: apilar discos 0 y 1 en la ubicación B. Esto se logra haciendo las acciones definidas en el párrafo anterior, con la excepción de que la ubicación objetivo es B para el subproblema. Una vez realizada esta subtarea, el disco 2 se puede mover directamente a la meta final, ubicación C. Ahora, resolvemos el problema moviendo los discos 0 y 1, los cuales están apilados en B, a la ubicación C, utilizando nuevamente un procedimiento como el descrito en el párrafo anterior.

Este relato de resolver una versión más compleja del problema de la Torre de Hanoi apunta a la naturaleza recursiva de dividir y conquistar: resolvemos el problema mayor por 0 1 2 3 4 A (Start) B (Spare) C (Goal) primero resolviendo una versión más pequeña del mismo tipo de problema. Para mover una pila de n discos a la ubicación C, primero movemos la pila más pequeña de n — 1 discos a la ubicación B. “Mover la pila” es el mismo tipo de procedimiento para los n discos y para los discos n — 1. Todo el enfoque es recursivo en el sentido de que para mover la pila grande, primero se debe usar el mismo procedimiento para mover la pila más pequeña sobre el disco más grande.

La naturaleza recursiva de la solución a la Torre de Hanoi se hace evidente si escribimos un algoritmo de pseudocódigo para mover los discos. Llamemos a nuestro procedimiento MoveStack (). Tomará cuatro argumentos: el número de discos en la pila a mover, la ubicación inicial, la ubicación de “repuesto” y la ubicación de la meta. Entonces, si tuviéramos una pila de tres discos en la ubicación A, y quisiéramos mover la pila a la ubicación C usando la ubicación B como repuesto, ejecutaríamos MoveStack (3, A, B, C).

La definición completa del procedimiento es la siguiente:

MoveStack (N, Inicio, Repuesto, Meta)

Si N = 0

Salir

Else

MoveStack (N — 1, Inicio, Meta, Repuesto)

MoveStack (1, Inicio, Repuesto, Meta)

MoveStack (N — 1, Repuesto, Inicio, Meta)

EnDiF

Observe la recursión explícita en este procedimiento, ya que MoveStack () se llama a sí mismo para mover una pila más pequeña de discos apilados en la parte superior del disco que va a mover. Tenga en cuenta también que la naturaleza recursiva de este programa significa que es lo suficientemente flexible como para trabajar con cualquier valor de N. La Figura 3-2 ilustra un estado intermedio que ocurre cuando este procedimiento se aplica a una versión de cinco discos del problema.

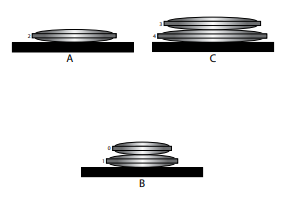
Figura 3-2. Un estado intermedio que ocurre cuando MoveStack () se aplica a una versión de cinco discos de la Torre de Hanoi.

En el código dado anteriormente, la recursión fue evidente porque MoveStack () se llamó a sí mismo. Hay otras formas en las que la recursión puede hacerse evidente. Por ejemplo, la recursión puede producir estructuras jerárquicas y autosimilares como los fractales (Mandelbrot, 1983), cuya naturaleza recursiva es inmediatamente evidente a través de la inspección visual. Consideremos el triángulo Sierpinski (Mandelbrot, 1983), que comienza como un triángulo equilátero (Figura 3-3).

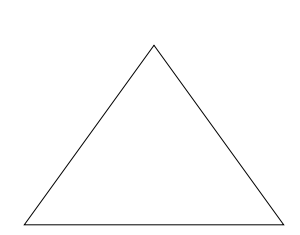
Figura 3-3. La raíz del triángulo Sierpinski es un triángulo equilátero.

El siguiente paso para crear el triángulo Sierpinski es tomar la Figura 3-3 y reducirlo exactamente a la mitad de su tamaño original. Tres de estos triángulos más pequeños se pueden inscribir dentro del triángulo original, como se ilustra en la Figura 3-4.

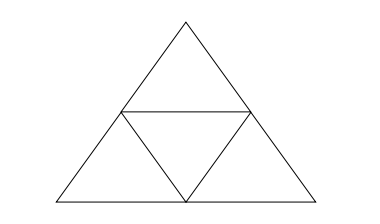
Figura 3-4. El segundo paso de construir un triángulo Sierpinski.

La regla utilizada para crear la Figura 3-4 se puede aplicar recursivamente y (en principio) infinitamente. Uno toma el triángulo más pequeño que se utilizó para crear la Figura 3-4, lo hace exactamente la mitad de su tamaño original, e inscribe tres copias de este triángulo aún más pequeño en cada uno de los tres triángulos que se utilizaron para crear la Figura 3-4. Esta regla se puede aplicar recursivamente para inscribir triángulos más pequeños en cualquiera de los triángulos que se agregaron a la figura en una etapa previa de dibujo. La Figura 3-5 muestra el resultado cuando esta regla se aplica cuatro veces a la Figura 3-4.

Figura 3-5. El triángulo Sierpinski que resulta cuando la regla recursiva se aplica cuatro veces a la Figura 3-4.

El triángulo Sierpinski, y todos los demás fractales que se crean por recursión, son intrínsecamente autosimilares. Es decir, si uno tomara uno de los triángulos más pequeños a partir de los cuales se construye la Figura 3-4 y lo magnificara, se vería todavía ver la estructura jerárquica que se ilustra anteriormente. La estructura del conjunto es idéntica a la estructura (más pequeña) de las partes. En la siguiente sección, vemos que la naturaleza recursiva del lenguaje humano se revela de la misma manera.