3.1.4: Identidades pitagóricas
- Page ID
- 107710
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Seno cuadrado más coseno cuadrado es igual a uno.
l Teorema de Pitágoras trabaja sobre triángulos rectos. Si considera que la coordenada x de un punto a lo largo del círculo unitario es el coseno y la coordenada y del punto es el seno y la distancia al origen es 1 entonces el Teorema de Pitágoras inmediatamente produce la identidad:
\(\begin{aligned} y^2+x^2&=1 \\ \sin ^2 x+\cos ^2 x&=1\end{aligned}\)
Un estudiante observador puede adivinar que existen otras identidades pitagóricas con el resto de funciones trigonométricas. ¿Es\(\tan ^2 x+\cot ^2 x=1\) una identidad legítima?
La prueba de la identidad pitagórica para seno y coseno es esencialmente dibujar un triángulo rectángulo en un círculo unitario, identificando el coseno como la coordenada x, el seno como la coordenada y y 1 como la hipotenusa.
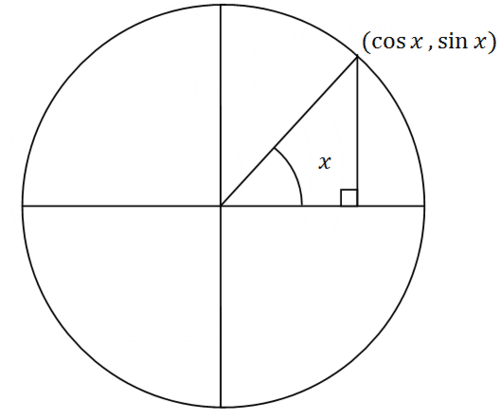
\(\cos ^2 x+\sin ^2 x=1\)
o
\(\sin ^2 x+\cos ^2 x=1\)
Las otras dos identidades pitagóricas son:
- \(1+\cot ^2 x=\csc ^2 x\)
- \(\tan ^2 x+1=\sec ^2 x\)
Para derivar estas dos identidades pitagóricas, dividir la identidad pitagórica original por\(\sin ^2 x\) y\(\cos ^2 x\) respectivamente.
Para derivar la identidad pitagórica\(1+\cot ^2 x=\csc ^2 x\) dividirla\(\sin ^2 x\) y simplificar.
\(\begin{aligned} \dfrac{\sin ^2 x}{\sin ^2 x}+\dfrac{\cos ^2 x}{\sin ^2 x}&=\dfrac{1}{\sin ^2 x}\\ 1+\cot ^2 x&=\csc ^2 x \end{aligned}\)
De igual manera, para derivar la identidad pitagórica\(\tan ^2 x+1=\sec ^2 x\), dividirla\(\cos ^2 x\) y simplificar.
\(\begin{aligned}\dfrac{\sin ^2 x}{\cos ^2 x}+\dfrac{\cos ^2 x}{\cos ^2 x} &=\dfrac{1}{\cos ^2 x}\\ \tan ^2 x+1 &=\sec ^2 x \end{aligned}\)
Anteriormente, se le preguntó si\(\tan ^2 x+\cot ^2 x=1\) es una identidad legítima. Las cofunciones no siempre están conectadas directamente a través de una identidad pitagórica.
\(\tan ^2 x+\cot ^2 x \neq 1\)
Solución
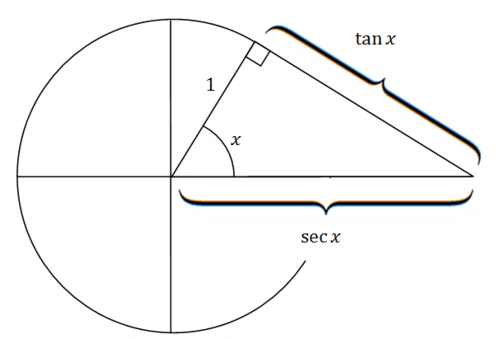
Visualmente, el triángulo rectángulo que conecta tangente y secante también se puede observar en el círculo unitario. La mayoría de la gente no sabe que tangente se denomina “tangente” porque se refiere a la distancia de la línea tangente desde el punto en el círculo unitario hasta el\(x\) eje. Mira la imagen de abajo y piensa en por qué tiene sentido eso\(\tan x\) y\(\sec x\) están como marcadas. \(\tan x=\dfrac{opp}{adj}\). Dado que el lado adyacente es igual a 1 (el radio del círculo),\(\tan x\) simplemente equivale al lado opuesto. Una lógica similar puede explicar la ubicación de\(\sec x\).
Simplifica la siguiente expresión:\(\dfrac{\sin x(\csc x−\sin x)}{1−\sin x}\).
Solución
\ (\ comenzar {alineado}
\ dfrac {\ sin x (\ csc x-\ sin x)} {1-\ sin x} &=\ dfrac {\ sin x\ cdot\ csc x-\ sin ^ {2} x} {1-\ sin x}\\
&=\ dfrac {1-\ sin ^ {2} x} {1-\ sin x}\
&=\ dfrac {(1-\ sin x) (1+\ sin x)} {1-\ sin x}\\
&=1+\ sin x
\ final {alineado}\)
Tenga en cuenta que factorizar la identidad pitagórica es una de las aplicaciones más potentes y comunes.
Demostrar la siguiente identidad trigonométrica:\((\sec ^2 x+\csc ^2 x)−(\tan ^2 x+\cot ^2 x)=2\)
Solución
Agrupar los términos y aplicar una forma diferente de las dos segundas identidades pitagóricas que son\(1+\cot ^2 x=\csc ^2 x\) y\(\tan ^2 x+1=\sec ^2 x\).
\(\begin{aligned} (\sec ^2 x+\csc ^2 x)−(\tan ^2 x+\cot ^2 x) &=\sec ^2 x−\tan ^2 x+\csc ^2 x−\cot ^2 x \\&=1+1\\&=2\end{aligned}\)
Simplifica la siguiente expresión. Nota:\(\sec ^2 x=\dfrac{1}{\cos ^2 x}\)
Solución
\((\sec ^2 x)(1−\sin ^2 x)−(\dfrac{\sin x}{\csc x}+\dfrac{\cos x}{\sec x})\)
\(\begin{aligned} (\sec ^2 x)(1−\sin ^2 x)−(\dfrac{\sin x}{\csc x}+\dfrac{\cos x}{\sec x})&=\sec ^2 x\cdot \cos ^2 x−(\sin ^2 x+\cos ^2 x) \\ &=1−1 \\&=0\end{aligned}\)
Simplifica la siguiente expresión.
\((\cos t−\sin t)^2+(cost+\sin t)^2\)
Solución
Obsérvese que inicialmente, la expresión no es la misma que la identidad pitagórica.
\(\begin{aligned} (\cos t−\sin t)^2+(\cos t+\sin t)^2&=\cos^2t−2\cos t \sin t+sin^2t+cos^2t+2 \cos t \sin t+\sin^2 t\\&=1−2\cos t \sin t+1+2\cos t \sin t \\&=2\end{aligned}\)
Revisar
- Demostrar cada uno de los siguientes:
- \((1−\cos ^2 x)(1+\cot ^2 x)=1\)
- \(\cos x(1−\sin ^2 x)=cos^3 x\)
- \(\sin ^2 x=(1−\cos x)(1+\cos x)\)
- \(\sin x=\dfrac{\sin ^2 x+\cos ^2 x}{\csc x}\)
- \(sin^4x−cos^4x=\sin ^2 x−\cos ^2 x\)
- \(\sin ^2 x cos ^3x=(\sin ^2 x− \sin^4x)(\cos x)\)
Simplifica cada expresión tanto como sea posible.
- \(\tan^3x \csc^3x\)
- \(\dfrac{\csc^2x−1}{sec^2x}\)
- \(\dfrac{1−\sin ^2 x}{1+\sin x}\)
- \(\sqrt{1−\cos ^2 x}\)
- \(\dfrac{\sin ^2 x−sin^4 x}{\cos ^2 x}\)
- \((1+\tan ^2 x)(\sec ^2 x)\)
- \(\dfrac{\sin ^2 x+\tan ^2 x+\cos ^2 x}{\sec x}\)
- \(\dfrac{1+\tan ^2 x}{\csc ^2 x}\)
- \(\dfrac{1−\sin ^2 x}{\cos x}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.2.
El vocabulario
| Término | Definición |
|---|---|
| identidad | Una identidad es una oración matemática que involucra el símbolo “=” que siempre es verdadera para las variables dentro de los dominios de las expresiones de ambos lados. |
| Identidad pitagórica | La identidad pitagórica es una relación que muestra que el seno de un ángulo cuadrado más el coseno de un ángulo cuadrado es igual a uno. |
| Teorema de Pitágoras | El Teorema de Pitágoras es una relación matemática entre los lados de un triángulo rectángulo\(a^2+b^2=c^2\), dada por, donde a y b son patas del triángulo y c es la hipotenusa del triángulo. |
Recursos adicionales
Video: Las identidades recíprocas, cocientes y pitagóricas
Práctica: Identidades pitagóricas

