1.5.3: Combinar transformaciones

Gráficas de funciones: Transformaciones combinadas

¿Cómo las diferentes formas de transformaciones dan como resultado las diferencias entre las funciones principales básicas que hemos explorado y algunas de las gráficas más complejas que pudo haber visto? Probablemente se le ha ocurrido que estas transformaciones individuales no son suficientes para dar como resultado diferencias tan significativas. ¿Cómo aplicamos entonces las transformaciones individuales para que se entiendan las gráficas más complejas?

---

Transformaciones de funciones: transformaciones combinadas

Al combinar turnos, reflexiones y estiramientos y compresión verticales y horizontales, un gráfico de función padre simple puede representar una función mucho más avanzada.

Considera la ecuación y=2 (x−3) ² +1. Podemos comparar la gráfica de esta función con la gráfica del padre y=x ²: la gráfica representa un estiramiento vertical por un factor de 2, un desplazamiento horizontal de 3 unidades a la derecha y un desplazamiento vertical de 1 unidad.

Podemos usar esta relación para graficar la función y=2 (x−3) ² +1. Puedes comenzar por bosquejar y=x ² o y=2x ². Después se puede desplazar la gráfica 3 unidades a la derecha, y subir 1 unidad.

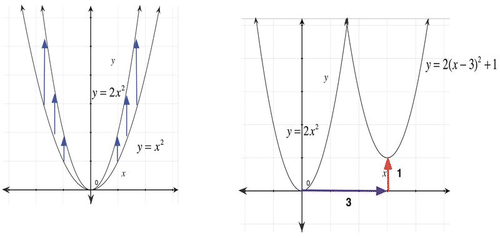[Figura1]

Usando tu conocimiento de la función padre y=|x| y tu conocimiento de las transformaciones, grafica la siguiente función:

f (x) =−|x|+3

La gráfica padre de esta función es la gráfica de y=|x|, reflejada sobre el eje x, y desplazada hacia arriba 3 unidades. La pregunta es: ¿qué transformación realiza primero?

Podemos responder a esta pregunta si consideramos algunos valores clave de función. La siguiente tabla muestra varios valores de función para f (x) =−|x|+3:

x	f (x) =−abs (x) +3
-3	−abs (−3) +3=− (+3) +3=−3+3=0
-2	−abs (−2) +3=− (+2) +3 = −2+3=1
-1	2
0	3
1	2
3	0

A partir de los valores de función en la tabla podemos ver que la función aumenta hasta un vértice en (0, 3), y luego vuelve a disminuir. Esto nos dice que podemos obtener la gráfica si primero reflejamos y=|x| sobre el eje x (volteamos la “v” boca abajo), y luego desplazamos la gráfica hacia arriba 3 unidades.

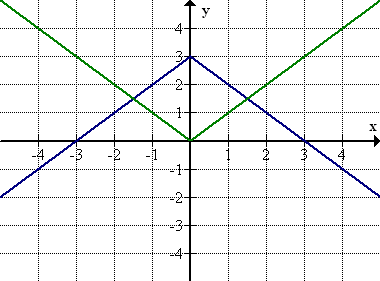[Figura2]

También podemos justificar este ordenamiento de las transformaciones de pensamos en el orden de las operaciones. Para encontrar cualquier valor de función tomamos un valor x, encontramos su valor absoluto, encontramos el negativo de ese número, y luego sumamos 3. Esto es lo mismo que el orden de la transformación: la reflexión viene antes de cambiar hacia arriba.

Al describir la relación entre una gráfica transformada y su gráfica padre, es importante tener cuidado con el orden de las operaciones. Toma la gráfica de f (x) =3 (x+7) ³ +5 y su función padre g (x) =x ³.

La gráfica de f (x) =4 (x+8) ^{3 −3} es la gráfica de g (x) =x ³, estirada verticalmente (hecha más estrecha) por un factor de 3, desplazada 7 unidades hacia la izquierda, y luego desplazada 5 unidades hacia arriba.

---

Ejemplos

Ejemplo 1

Grafica la función a continuación usando tu conocimiento de la función padre y=|x| y tu conocimiento de las transformaciones.
g (x) =|−x+3|

Solución

Esta función representa un desplazamiento horizontal de y=|x|, y una reflexión sobre el eje x. Antes de graficar, considere algunos valores de función:

x	g (x) =abs (−x+3)
-3	abs (− (−3) +3) =abs (3+3) =abs (6) =6
-2	abs (− (−2) +3) = (2+3) =abs (5) =5
0	3
1	2
3	0
4	1

De los valores en la tabla, podemos ver que el vértice de la gráfica está en (3, 0). A continuación se muestra la gráfica.

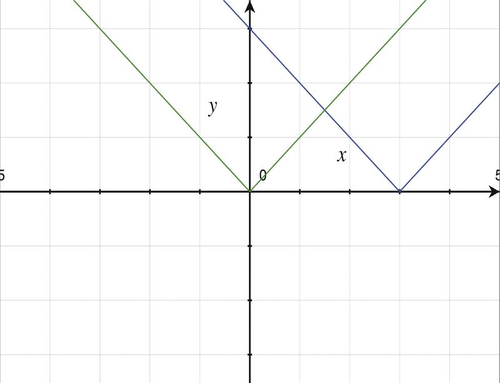[Figura3]

La gráfica se ve igual que la gráfica de y=|x−3|. Este es el caso porque y=|−x+3|=|− (x−3) |, y porque |−a|=|a| para todos los valores de a, luego |− (x−3) |=|x−3|. Entonces la función original es igual a |x−3|.

Todavía podemos pensar en esta gráfica como una reflexión: si reflejamos y=|x| sobre el eje x, la gráfica sigue siendo la misma, ya que es simétrica sobre el eje x. Después desplazamos la gráfica 3 unidades a la derecha. Lo que es importante señalar aquí es que para “leer” la ecuación como un desplazamiento horizontal, se debe negar toda la expresión dentro de la función (en este caso, dentro del valor absoluto).

Recuerda que la clave de múltiples transformaciones es hacerlas en orden. Otra forma de hacer un seguimiento de qué operaciones hacer en qué orden es simplemente hacerlas en el orden en que aparecen en la ecuación, de izquierda a derecha.

Ejemplo 2

Dibuja el gráfico de y=−3 (x+2) ² +4

Solución

Para bosquejar y=−3 (x+2) ² +4, comenzamos con la función padre, y=x ².

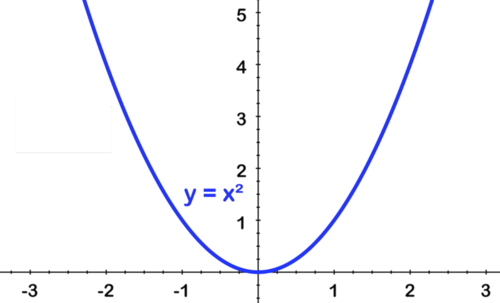[Figura4]

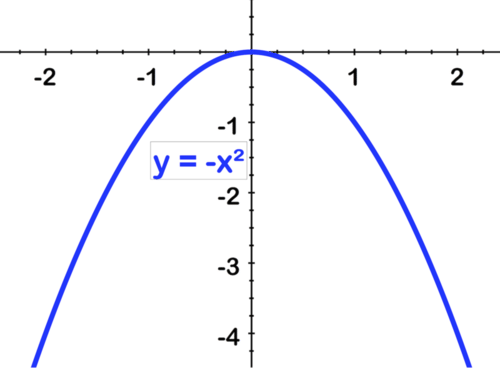[Figura5]

A continuación estiramos por 3:

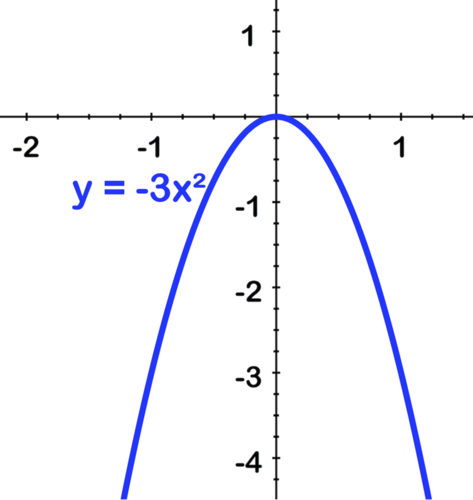[Figura6]

Desplazar a la izquierda por 2:

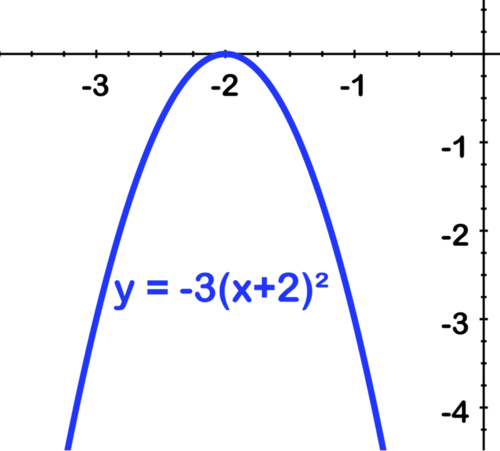[Figura7]

Finalmente cambiar hacia arriba por 4:

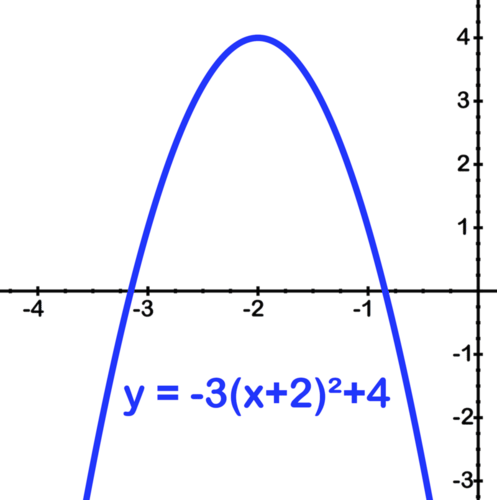[Figura8]

Ejemplo 3

Esbozar el gráfico de y=−1|x+2|−3

Solución

Para esbozar y=−1|x+2|−3 comienza con la ecuación padre: f (x) =|x| y completa las transformaciones de izquierda a derecha:

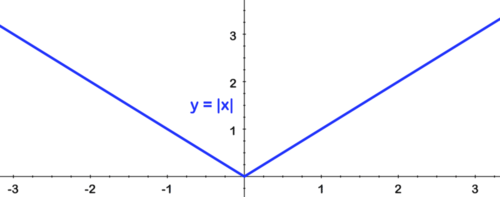[Figura9]

Primero reflexione sobre el eje x:

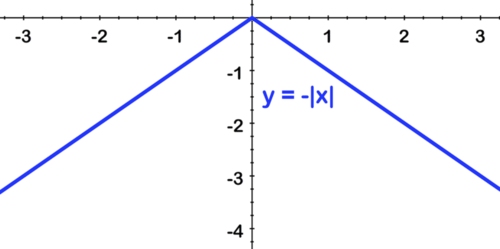[Figura10]

Segundo, desplazamiento a la izquierda por 2:

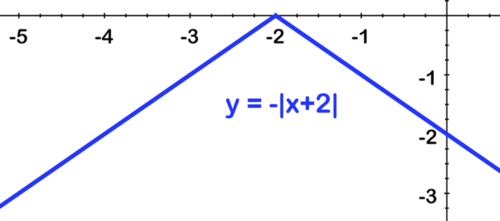[Figura11]

Por último, cambiar a la baja por 3:

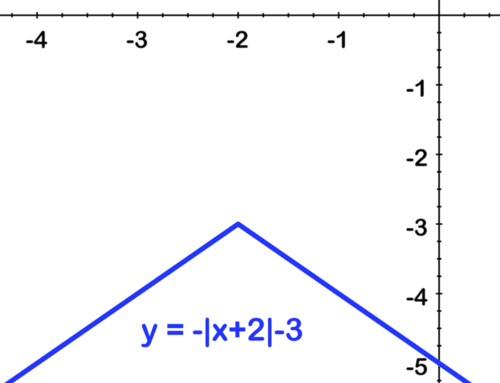[Figura12]

Ejemplo 4

Dibuje el gráfico de f (x) =2 (x−1) ²

Solución

Para esbozar f (x) =2 (x−1) ² comienza con el padre f (x) =x ²

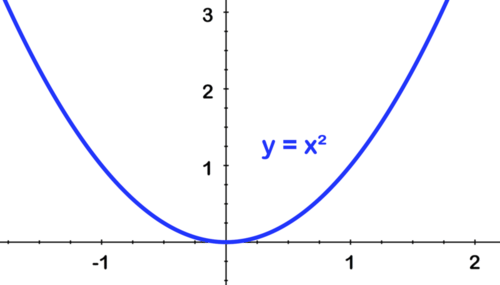[Figura13]

Primer tramo por 2:

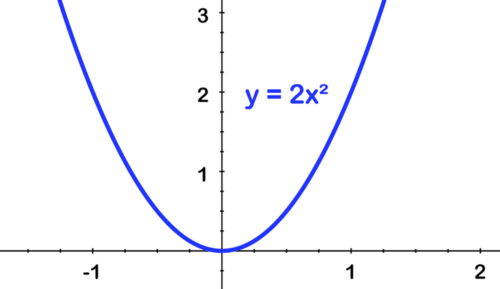[Figura14]

Segundo, cambiar a la derecha por 1:

[Figura15]

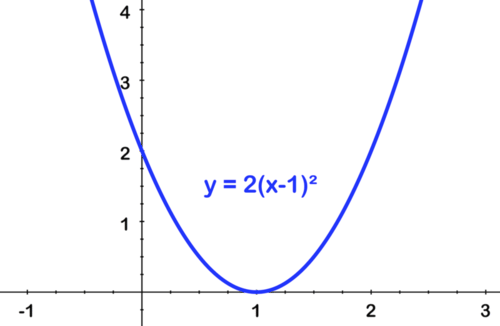Ejemplo 5

Esbozar el gráfico de\(\ f(x)=-2 \sqrt{x-1}\)

Solución

Para bosquejar la gráfica de\(\ f(x)=-2 \sqrt{x-1}\) inicio con el padre\(\ y=\sqrt{x}\)

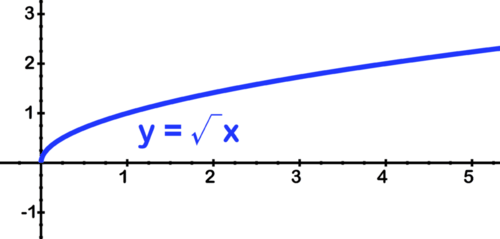[Figura16]

Primero reflexione sobre el eje x:

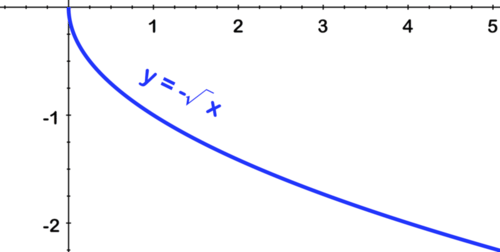[Figura17]

Segundo, estirar por 2:

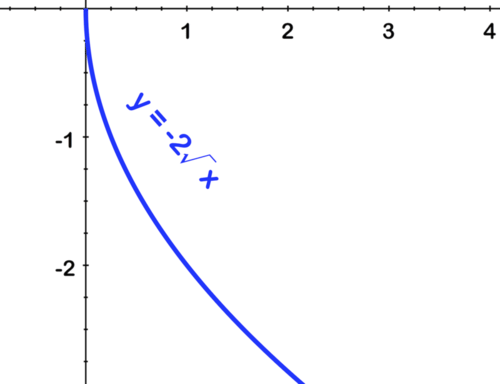[Figura18]

Tercero, cambiar a la derecha por 1:

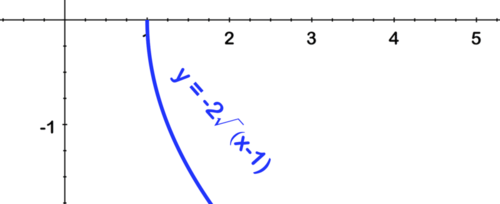[Figura19]

---

Revisar

1. ¿Qué parte de la función g (x) =− (f (x) +1) =− (x ³ +1) desplaza la gráfica de f (x) verticalmente?
2. ¿Qué parte de la función g (x) =− (f (x) +1) refleja la gráfica de f (x) a través del eje x?
3. ¿Qué diferencia hay entre las funciones g (x) =− (x ³ +1.0) y h (x) =−x ³ +1.0 que cambia la apariencia de la gráfica?
4. Dada la función g (x) =3.0 (f (x) +2.0) =3.0 (x ² +2.0), ¿qué es lo que desplaza la gráfica de f (x) verticalmente?
   1. 3.0
   2. x ²
   3. 2.0
5. Dada la función g (x) =3.0 (f (x) +2.0) =3.0 (x ² +2.0), ¿qué es lo que estira la gráfica de f (x) verticalmente?
   1. 3.0
   2. x ²
   3. 2.0
6. ¿Qué parte de la ecuación k (x) =− (x+1) ³ desplaza la gráfica de j (x) =x ³ horizontalmente?
7. ¿Qué parte de la ecuación k (x) =− (x+1) ³ refleja la gráfica de j (x) =x ³ a través del eje x?
8. Dada la función g (x) =3.0 (f (x) +2.0) =3.0 (x+2.0) ³, ¿qué es lo que desplaza la gráfica de f (x) horizontalmente?
9. Dada la función g (x) =3.0 (f (x) +2.0) =3.0 (x ² +2.0) ³, ¿qué es lo que estira la gráfica de f (x) verticalmente?
10. La gráfica de g (x) es f (x) reflejada a través del eje x. La gráfica de h (x) es f (x) reflejada a través del eje y. La gráfica de j (x) es f (x) reflejada a través del eje x y el eje y. Al graficar j (x) ¿importa el orden en que ocurren las reflexiones? (¿Importa en qué eje reflejemos primero la gráfica?)
11. Dada la función f (x) =x ³, escribe una función g (x) que es: f (x) reflejada a través del eje y y luego estirada verticalmente por 8.
12. ¿Cómo se transforma la gráfica de: f (x) =x ³ para que se vea como la gráfica de: f (x) =4x ³ +6?
    1. Estirarlo por un factor de\(\ 1 \over 4\) y desplazarlo hacia arriba 6 unidades.
    2. Estirarlo por un factor de 6 y desplazarlo a la izquierda 4 unidades.
    3. Estirarlo por un factor de 4 y desplazarlo hacia abajo 6 unidades.
    4. Estirarlo por un factor de 4 y desplazarlo hacia arriba 6 unidades.
13. ¿Cómo se transforma la gráfica de:\(\ f(x)=\sqrt{x}\) para que se vea como la gráfica de:\(\ f(x)=-\sqrt{x}-4\)?
    1. Refleja el eje x y deslízalo 4 unidades hacia abajo.
    2. Refleja a través del eje y y desplace 4 unidades hacia arriba.
    3. Refleja a través del eje x y desplace 4 unidades hacia arriba.
    4. Refleja a través del eje y y deslízalo 4 unidades hacia abajo.
14. La gráfica a continuación es una transformación de una función común. ¿Cuál es la función común que se ha transformado?
    1. y=|x|
    2. y=\(\ \sqrt{x}\)
    3. y=x ²
    4. y=x ³

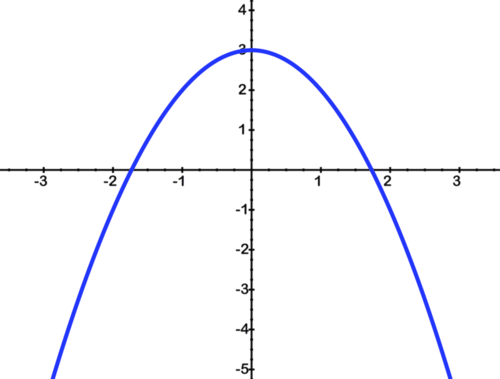[Figura20]

15. ¿Cómo se ha transformado la función en Q# 14?
    1. Reflejado a través del eje y y desplazado hacia la derecha 3 unidades.
    2. Estirada verticalmente por un factor de 3 y desplazada a la derecha 1 unidad.
    3. Reflejado a través del eje x y desplazado hacia arriba 3 unidades.
    4. Reflejado a través del eje x y desplazado a la izquierda 4 unidades.
16. Escribe una función g (x) cuya gráfica se parezca a la gráfica de f (x) =|x| reflejada a través del eje x y desplazada hacia arriba 1 unidad.
17. Elija la función cuya gráfica se vea como la gráfica de f (x) =x ³ desplazada hacia la derecha 2 unidades y reflejada a través del eje y.
    1. f (x) = (−x−2) ³
    2. f (x) = (−x+2) ³
    3. f (x) =− (x−2) ³
    4. f (x) = (x−2) ³

---

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.7.

---

El vocabulario

Término	Definición
función padre	Una función padre es la forma más simple de un tipo particular de función. Todas las demás funciones de este tipo suelen compararse con la función padre.
Transformaciones	Las transformaciones se utilizan para cambiar la gráfica de una función padre en la gráfica de una función más compleja.

---

Atribuciones de imagen

1. [Figura 1]
   Licencia: CC BY-NC-SA
2. [Figura 2]
   Licencia: CC BY-NC-SA
3. [Figura 3]
   Licencia: CC BY-NC-SA
4. [Figura 4]
   Licencia: CC BY-NC-SA
5. [Figura 5]
   Licencia: CC BY-NC-SA
6. [Figura 6]
   Licencia: CC BY-NC-SA
7. [Figura 7]
   Licencia: CC BY-NC-SA
8. [Figura 8]
   Licencia: CC BY-NC-SA
9. [Figura 9]
   Crédito: dev Moore; Fundación CK-12
   Fuente: https://www.flickr.com/photos/devinmoore/187215281/in/photolist-hxwzF-9Y2dT2-8R5iar-9Y2cLM-ePfP1W-eP4pca-epUxUk-ePfP4W-ceh8k3-3dMceZ-aehC8w-gmZd-e3dfr7-ac7c3c-dMr5kM-6bfCWV-6vpzyo-eKFqm1-iEv4o-aYNoV6-aWuFqv-9Uomhm-aWuFb4-eLWJx6-9Y2d4v-aWuFg4-633FZc-7L1mSC-aWuFn6-eKFqkC-7nAuor-9yD6vQ-7jAj2m-aWuFja-bXcHpR-7q9MQ4-eq QMBS-4V9IRC-4V9ISQ-EPFPIS-9mmCH4-7QEAJQ-EPFNZY-B3SGM-EP4OK2-EP4OZD-7Q9Y2K-EPF9O-EKFXDM-7QDVYU
   Licencia: CC BY-NC-SA
10. [Figura 10]
    Crédito: dev Moore; Fundación CK-12
    Fuente: https://www.flickr.com/photos/devinmoore/187215281/in/photolist-hxwzF-9Y2dT2-8R5iar-9Y2cLM-ePfP1W-eP4pca-epUxUk-ePfP4W-ceh8k3-3dMceZ-aehC8w-gmZd-e3dfr7-ac7c3c-dMr5kM-6bfCWV-6vpzyo-eKFqm1-iEv4o-aYNoV6-aWuFqv-9Uomhm-aWuFb4-eLWJx6-9Y2d4v-aWuFg4-633FZc-7L1mSC-aWuFn6-eKFqkC-7nAuor-9yD6vQ-7jAj2m-aWuFja-bXcHpR-7q9MQ4-eq QMBS-4V9IRC-4V9ISQ-EPFPIS-9mmCH4-7QEAJQ-EPFNZY-B3SGM-EP4OK2-EP4OZD-7Q9Y2K-EPF9O-EKFXDM-7QDVYU
    Licencia: CC BY-NC-SA
11. [Figura 11]
    Crédito: dev Moore; Fundación CK-12
    Fuente: https://www.flickr.com/photos/devinmoore/187215281/in/photolist-hxwzF-9Y2dT2-8R5iar-9Y2cLM-ePfP1W-eP4pca-epUxUk-ePfP4W-ceh8k3-3dMceZ-aehC8w-gmZd-e3dfr7-ac7c3c-dMr5kM-6bfCWV-6vpzyo-eKFqm1-iEv4o-aYNoV6-aWuFqv-9Uomhm-aWuFb4-eLWJx6-9Y2d4v-aWuFg4-633FZc-7L1mSC-aWuFn6-eKFqkC-7nAuor-9yD6vQ-7jAj2m-aWuFja-bXcHpR-7q9MQ4-eq QMBS-4V9IRC-4V9ISQ-EPFPIS-9mmCH4-7QEAJQ-EPFNZY-B3SGM-EP4OK2-EP4OZD-7Q9Y2K-EPF9O-EKFXDM-7QDVYU
    Licencia: CC BY-NC-SA
12. [Figura 12]
    Crédito: dev Moore; Fundación CK-12
    Fuente: https://www.flickr.com/photos/devinmoore/187215281/in/photolist-hxwzF-9Y2dT2-8R5iar-9Y2cLM-ePfP1W-eP4pca-epUxUk-ePfP4W-ceh8k3-3dMceZ-aehC8w-gmZd-e3dfr7-ac7c3c-dMr5kM-6bfCWV-6vpzyo-eKFqm1-iEv4o-aYNoV6-aWuFqv-9Uomhm-aWuFb4-eLWJx6-9Y2d4v-aWuFg4-633FZc-7L1mSC-aWuFn6-eKFqkC-7nAuor-9yD6vQ-7jAj2m-aWuFja-bXcHpR-7q9MQ4-eq QMBS-4V9IRC-4V9ISQ-EPFPIS-9mmCH4-7QEAJQ-EPFNZY-B3SGM-EP4OK2-EP4OZD-7Q9Y2K-EPF9O-EKFXDM-7QDVYU
    Licencia: CC BY-NC-SA
13. [Figura 13]
    Licencia: CC BY-NC-SA
14. [Figura 14]
    Licencia: CC BY-NC-SA
15. [Figura 15]
    Licencia: CC BY-NC-SA
16. [Figura 16]
    Licencia: CC BY-NC-SA
17. [Figura 17]
    Licencia: CC BY-NC-SA
18. [Figura 18]
    Licencia: CC BY-NC-SA
19. [Figura 19]
    Licencia: CC BY-NC-SA
20. [Figura 20]
    Licencia: CC BY-NC-SA