6.2.4: Parábolas y Geometría Analítica

Parábolas y Geometría Analítica

Brandyn está graficando parábolas como parte de su tarea. Está familiarizado con la forma estándar de una parábola:\(\ y=a x^{2}\), y la forma más larga:\(\ y-k=a(x-h)^{2}\).

En su tercer problema, se encuentra con un inconveniente. Ha simplificado la ecuación significativamente, y ha estado tratando de que se ajuste a la forma estándar, pero sigue ideando esto:\(\ x-4=3(y-3)^{2}\). No puede entender por qué el término y es el cuadrado, en lugar del término x.

¿Qué está pasando aquí?

---

Parábolas y Geometría Analítica

Esta es nuestra segunda lección sobre parábolas. En la lección inicial, exploramos la parábola usando la fórmula de distancia, y tocamos el uso del enfoque y la directriz. En esta lección, primero examinamos las parábolas desde el punto de vista de la “geometría analítica”, y luego trabajamos algunos ejemplos con el enfoque y la directriz de una parábola.

Encontrar la ecuación de una parábola usando geometría analítica

Considere un cono orientado en el espacio como se muestra a continuación:

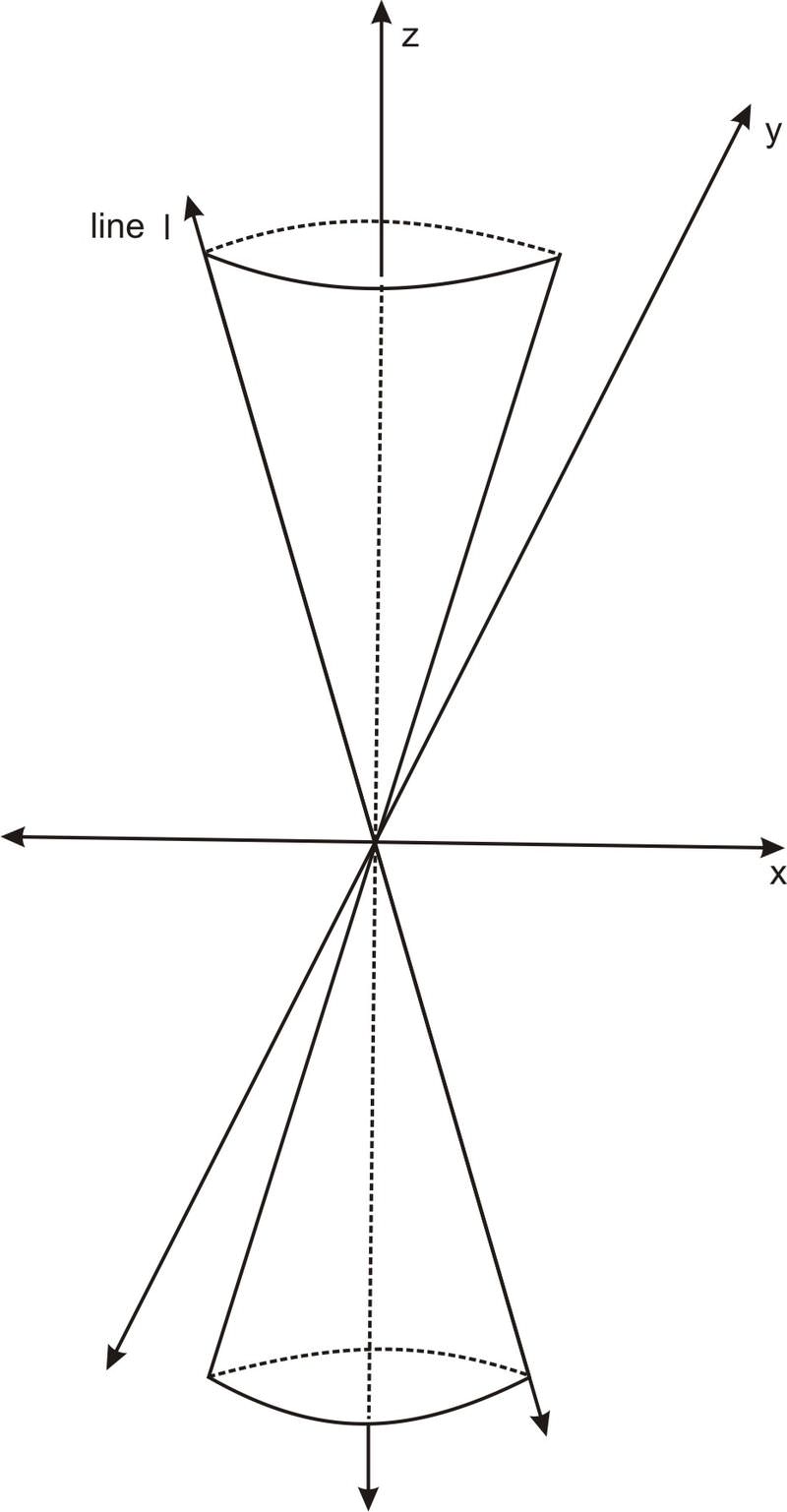
Si el cono se abre en un ángulo tal que en cualquier punto su relación de radio a altura es a, entonces el cono podría definirse como el conjunto de puntos de tal manera que la distancia desde el eje z es a veces la coordenada z. O, en otras palabras, el conjunto de puntos (x, y, z) que satisface:

\(\ \sqrt{(x-0)^{2}+(y-0)^{2}}=a z\)

o

\(\ x^{2}+y^{2}=a^{2} z^{2}\)

Esta ecuación funciona para valores negativos de x, y y z, dando la ecuación general para un cono de dos lados.

Para considerar la intersección de este cono con un plano que es paralelo a la línea\(\ l\) marcada en el diagrama anterior, lo más conveniente es rotar todo el cono alrededor del\(\ y\) eje hasta que el lado izquierdo del cono esté vertical, luego cruzarlo con un plano vertical perpendicular al \(\ x\)−eje. Tal rotación deja la\(\ y\) variable −sin cambios. Para ver qué le hace a las\(\ z\) variables\(\ x\) y, veamos qué sucede con el punto\(\ (x,z)\) en el\(\ xz\) plano −cuando se gira un ángulo de θ.

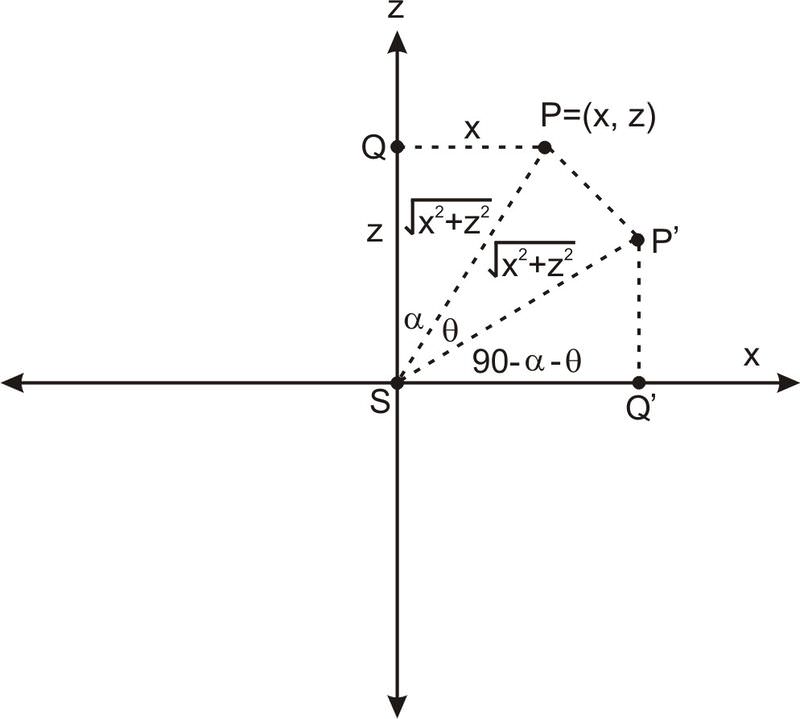
En el diagrama anterior,\(\ P(x, z)\) se gira un ángulo de θ con respecto al punto\(\ P^{\prime}\). Hemos marcado las longitudes laterales\(\ Q P=x\) y\(\ S Q=z\). Por el teorema de Pitágoras,\(\ S P=\sqrt{x^{2}+z^{2}}\). También tenemos\(\ S P^{\prime}=\sqrt{x^{2}+z^{2}}\), ya que la rotación deja sin cambios la distancia desde el origen. Para encontrar las\(\ x\) coordenadas −de nuestro punto girado\(\ P^{\prime}\), podemos usar el hecho de que

\(\ \cos (90-\alpha-\theta)=\frac{S Q^{\prime}}{\sqrt{x^{2}+z^{2}}}\). Pero por propiedades del coseno tenemos:

\(\ \cos (90-\alpha-\theta)=\sin (\alpha+\theta)\),

y sustituyendo con la fórmula de adición sinusoidal nos da:

\(\ \frac{S Q^{\prime}}{\sqrt{x^{2}+z^{2}}}=\sin (\alpha) \cos (\theta)+\cos (\alpha) \sin (\theta)\),

que podemos usar nuestro diagrama para cambiar a:

\(\ \frac{S Q^{\prime}}{\sqrt{x^{2}+z^{2}}}=\frac{x}{\sqrt{x^{2}+z^{2}}} \cos (\theta)+\frac{z}{\sqrt{x^{2}+z^{2}}} \sin (\theta)\)

lo que simplifica a:

\(\ S Q^{\prime}=x \cos (\theta)+z \sin (\theta)\)

Para encontrar las\(\ x\) coordenadas −de nuestro punto girado\(\ P^{\prime}\), podemos usar el hecho de que

\(\ \sin (90-\alpha-\theta)=\frac{P^{\prime} Q^{\prime}}{\sqrt{x^{2}+z^{2}}}\). Pero por propiedades de seno tenemos:

\(\ \sin (90-\alpha-\theta)=\cos (\alpha+\theta)\)

y sustituyendo con la fórmula de adición de coseno nos da:

\(\ \frac{P^{\prime} Q^{\prime}}{\sqrt{x^{2}+z^{2}}}=\cos (\alpha) \cos (\theta)-\sin (\alpha) \sin (\theta)\),

que podemos usar nuestro diagrama para cambiar a:

\(\ \frac{P^{\prime} Q^{\prime}}{\sqrt{x^{2}+z^{2}}}=\frac{z}{\sqrt{x^{2}+z^{2}}} \cos (\theta)-\frac{x}{\sqrt{x^{2}+z^{2}}} \sin (\theta)\)

lo que simplifica a:

\(\ P^{\prime} Q^{\prime}=z \cos (\theta)-x \sin (\theta)\)

Mirando hacia atrás a la imagen, esto significa que las coordenadas de\(\ P^{\prime}\) son\(\ (x \cos (\theta)+z \sin (\theta), z \cos (\theta)-x \sin (\theta))\). En otras palabras, al rotar de\(\ P\) a\(\ P^{\prime}\), la\(\ x\) coordenada −cambia a\(\ x \cos (\theta)+z \sin (\theta)\) y la coordenada\(\ z\) − cambia a\(\ z \cos (\theta)-x \sin (\theta)\).

Si esta rotación sucede a cada punto del cono, podemos sustituir\(\ x\) y\(\ x \cos (\theta)+z \sin (\theta)\)\(\ z \cos (\theta)-x \sin (\theta)\) para\(\ z\) dentro de nuestra ecuación del cono, resultando en una nueva ecuación para el cono después de rotar por\(\ \theta\).

\ (\\ comenzar {alineado}
(x\ cos (\ theta) +z\ sin (\ theta)) ^ {2} +y^ {2} &=a^ {2} (z\ cos (\ theta) -x\ sin (\ theta)) ^ {2}\
x^ {2}\ cos ^ {2} (\ theta) +2 x\ z cos (\ theta)\ sin (\ theta) +z^ {2}\ sin ^ {2} (\ theta) +y^ {2} &=a^ {2}\ left (x^ {2}\ sin ^ {2} (\ theta) -2 x z\ cos (\ theta)\ sin (\ theta) +z^ {2} \ cos ^ {2} (\ theta)\ derecho.) \\
x^ {2}\ cos ^ {2} (\ theta) +2 x z\ cos (\ theta)\ sin (\ theta) +z^ {2}\ sin ^ {2} (\ theta) +y^ {2} &=a^ {2} x^ {2}\ sin ^ {2} (\ theta) -2 a^ {2} x\ cos (\ theta) -2 a^ {2} x\ cos (\ theta))\ sin (\ theta) +a^ {2} z^ {2}\ cos (\ theta))\\
x^ {2}\ cos ^ {2} (\ theta) +2 x z\ cos (\ theta)\ sin (\ theta) +z^ {2}\ sin ^ {2} (\ theta) +y^ {2} &=a^ {2} x^ {2}\ sin ^ {2} (\ theta) -2 a^ {2} x z\ cos (\ theta)\ sin (\ theta) +a^ {2} z^ {2}\ cos (\ theta))
\ final {alineado}\)

Ahora en el caso del cono inclinado, queremos inclinar el cono de tal manera que el lado izquierdo se vuelva vertical. Dado que el factor\(\ a\) determina qué tan inclinado está el cono, podemos ver desde el triángulo debajo de eso\(\ \sin (\theta)=\frac{a}{\sqrt{1+a^{2}}}\) y\(\ \cos (\theta)=\frac{1}{\sqrt{1+a^{2}}}\).

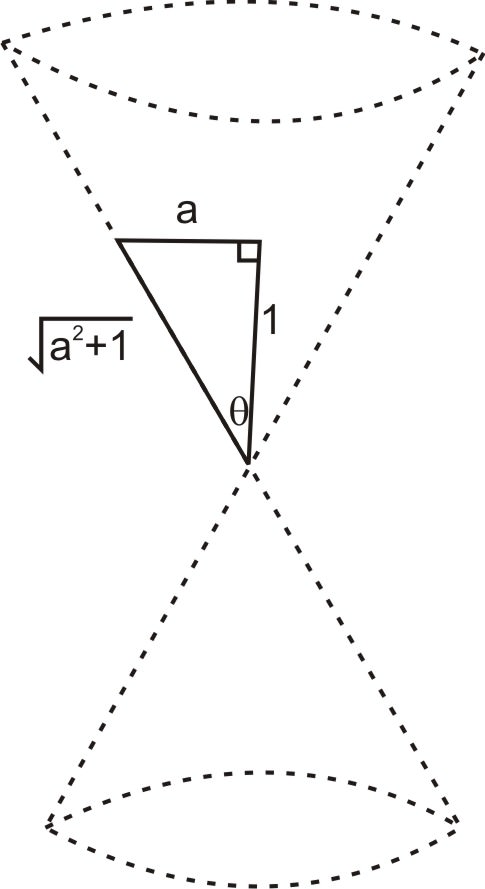
Entonces la ecuación se convierte en:

\ (\\ begin {alineado}
x^ {2}\ frac {1} {1+a^ {2}} +2 x z\ frac {a} {1+a^ {2}} +z^ {2}\ frac {a^ {2}} {1+a^ {2}} +y^ {2} &=a^ {2} x^ {2}\ frac {a^ {2}}} {1+a^ {2}} -2 a^ {2} x z\ frac {a} {1+a^ {2}} +a^ {2} z^ {2}\ frac {1} {1+a^ {2}}\
x^ {2} +2 x z a+z^ {2} a^ {2} a^ {2} +y^ {2}\ izquierda (1+a^ {2}\ derecha) &=a^ {4} x^ {2} -2 a^ {3} x z+a^ {2} z^ {2}\\
x^ {2} +2 x z a+y^ {2}\ izquierda (1+a^ {2}\ derecha) &=a^ {4} x^ {2} -2 a^ {3} x z
\ end {alineado}\)

Ahora que hemos inclinado nuestro cono, para tomar una sección transversal que es paralela al lado izquierdo del cono, simplemente podemos cortarlo con un plano vertical. La ecuación de un plano vertical que atraviesa\(\ (b, 0,0)\) y perpendicular al\(\ x\) eje −es\(\ x=b\). Por lo tanto, establecer\(\ x\) igual a la constante en la ecuación anterior nos dará la intersección del cono inclinado y un plano paralelo a un lado del cono. \(\ b\). Aquí hay una imagen de la rotación y la sección transversal, que se encuentra en un\(\ xz\) plano −.

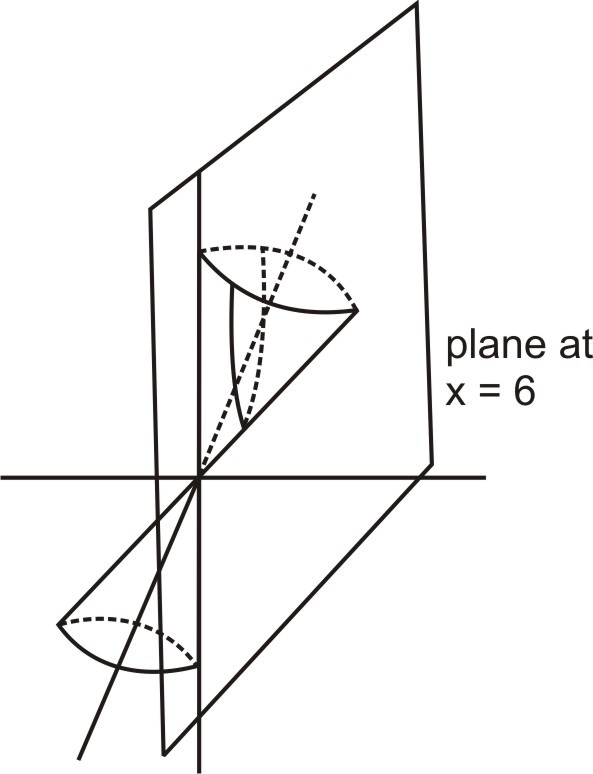
Estableciendo\(\ x\) igual a la constante\(\ b\), tenemos:

\ (\\ comenzar {alineado}
b^ {2} +2 a b z+y^ {2}\ izquierda (1+a^ {2}\ derecha) &=a^ {4} b^ {2} -2 a^ {3} b z\\
z\ izquierda (2 a b+2 a^ {3} b\ derecha) &=-y^ {2}\ izquierda (1+a^ {2}\ derecha) +a^ {4} b^ {2} -b^ {2}\\
z &=\ izquierda (\ frac {-1-a^ {2}} {2 a b+2 a^ {3} b}\ derecha) y^ {2} +\ izquierda (a^ {4} b^ {2} -b^ {2}\ derecha)
\ end {alineado}\)

Si bien este coeficiente y término constante parecen complicados,\(\ a\) y\(\ b\) pueden elegirse para que el coeficiente del\(\ y^{2}\) término pueda ser igual a cualquier número (explorarás este hecho en un ejercicio). El término constante puede ser ignorado ya que cualquier parábola puede ser desplazada verticalmente en cualquier cantidad.

Entonces la forma general de una parábola es:

\(\ z=A y^{2}\)

donde A es cualquier constante.

O, usando el más estándar\(\ x-\) y\(\ y-\text { coordinates }\) la forma de una parábola es

\(\ y=a x^{2}\)

Como antes, esta ecuación se puede adaptar para producir las formas desplazadas y orientadas horizontalmente.

---

Ejemplos

Ejemplo 1

Anteriormente, se le hizo una pregunta sobre Brandyn, quien no está seguro de por qué tiene un\(\ y^{2}\) término en su ecuación de forma estándar en lugar de un\(\ x^{2}\) término.

Solución

Brandyn sigue ideando un\(\ y^{2}\) término porque se trata de una parábola lateral.

Ejemplo 2

En la prueba anterior, simplificamos enormemente la fórmula cerca del final sustituyendo A por

\(\ \frac{-1-a^{2}}{2 a b+2 a^{3} b}\)

Solución

Explique por qué esto era permisible demostrando que para cualquiera\(\ A\) existen constantes\(\ a\) y\(\ b\) tal que\(\ A=\frac{-1-a^{2}}{2 a b+2 a^{3} b}\)

Resolviendo para\(\ b\) en términos de\(\ A\) y\(\ a\), tenemos:

\ (\\ comenzar {alineado}
A\ izquierda (2 a b+2 a^ {3} b\ derecha) &=-1-a^ {2}\\
2 A a b\ izquierda (1+a^ {2}\ derecha) &=-\ izquierda (1+a^ {2}\ derecha)\\
2 A a b &=-1\\
2 A a b &=-1\\
b &=-\ frac {1} {2 A a}
\ final {alineado}\)

Para que podamos establecer\(\ b=2Aa\) y la relación se mantendrá.

Ejemplo 3

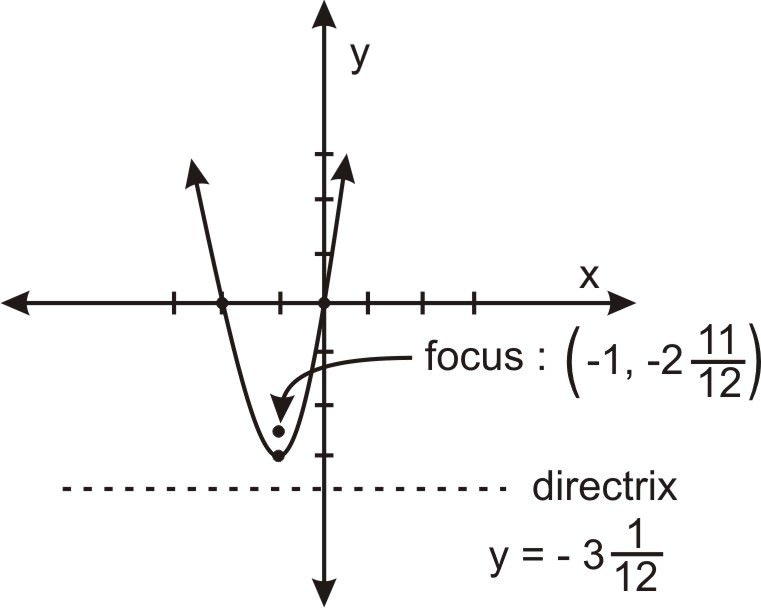
Dibuja un boceto de la siguiente parábola. Identificar también su directrix y enfoque. \(\ 3 x^{2}+6 x-y=0\)

Solución

Factorizar y completar el cuadrado para obtener:\(\ 3(x+1)=y+3\). El vértice está en:\(\ (-1,-3)\).

El foco es\(\ \left(-1,-2 \frac{11}{12}\right)\) La directrix es la línea\(\ y=-3 \frac{1}{12}\)

Ejemplo 4

Encuentra la ecuación para una parábola con directrix\(\ y=-2\) y enfoque\(\ (3,8)\).

Solución

El vértice se encuentra verticalmente a medio camino entre el foco y la directriz:\(\ \frac{-2+8}{2}=3\), lo mismo horizontalmente que el foco:\(\ x=3\) y por lo tanto en:\(\ (3,3)\).

Sustituir esos valores en la fórmula da:

\(\ y-3=\frac{1}{20}(x-3)^{2}\)

Ejemplo 5

Encuentra la ecuación para una parábola con directrix\(\ y=3\) y enfoque\(\ (2, -1)\).

Solución

Usando la forma de vértice de una parábola\(\ (y-k)^{2}=4 a(x-h)\):

Recordemos que el valor y del vértice\(\ k\) es el punto medio de la directriz y el foco en la línea perpendicular a la directriz y cruzando el foco. Por lo tanto, el valor y del vértice es 1

Recordemos que el valor x del vértice\(\ h\) es el mismo que el foco, por lo tanto, el valor x del vértice es 2

Por último, recordemos que\(\ a\) la distancia desde el vértice al foco o desde el vértice a la directriz (que son iguales):\(\ \therefore a=2\)

Sustituir da:\(\ (y-1)^{2}=8(x-2) \rightarrow y^{2}+1=8 x-16 \rightarrow y^{2}=8 x-17\)

Ejemplo 6

Describir la forma de una parábola en relación con un cono o cono doble.

Solución

La forma de una parábola en lo que se refiere a un cono o cono doble, es que una parábola representa la forma revelada cuando se corta un cono hueco en un ángulo igual al lado del cono. Particularmente claro con un cono doble es el hecho de que cortar a través de un ángulo más pronunciado dará como resultado dos curvas (una hipérbola) y un ángulo menos profundo dará como resultado una elipse.

Ejemplo 7

Dibuje la siguiente parábola e identifique la directriz y enfoque:\(\ 4 x^{2}-3 x+y=7\).

Solución

\(\ y=a x^{2}+b x+c\)... Recordemos la forma estándar de una parábola

\(\ a=-3|b=6| c=-2\)... Extracto a, b, c

\(\ x=\frac{-6}{2(-3)} \rightarrow x=1\)... La coordenada x del vértice\(\ =\frac{-b}{2 a}\)

\(\ y=(-3)(1)+6(1)-2\)... Sustituir el valor x calculado para resolver\(\ y\)

\(\ y=1\)... El vértice = (1,1)

\(\ x=1 \pm \frac{1}{\sqrt{3}}\)... Identificar las intercepciones x usando la fórmula cuadrática

---

Revisar

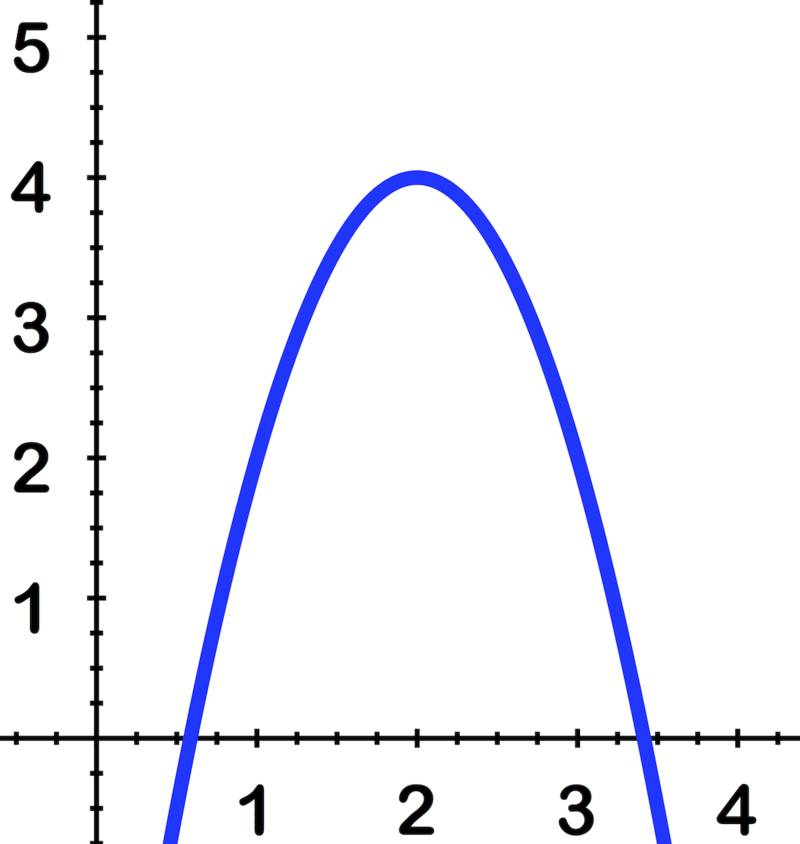
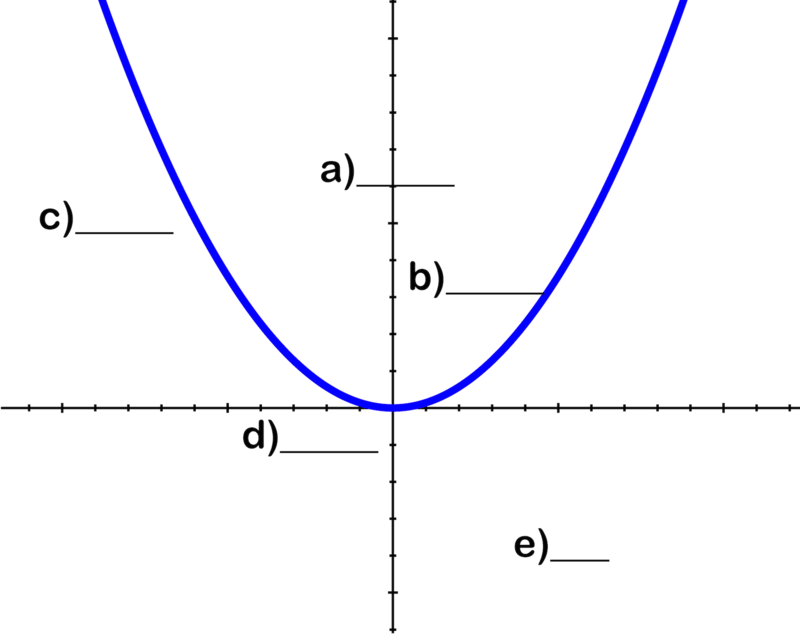
Usa la imagen para identificar las partes de la parábola:

1. El Foco
2. El vértice
3. El Radio Focal
4. La Directrix
5. La Parábola

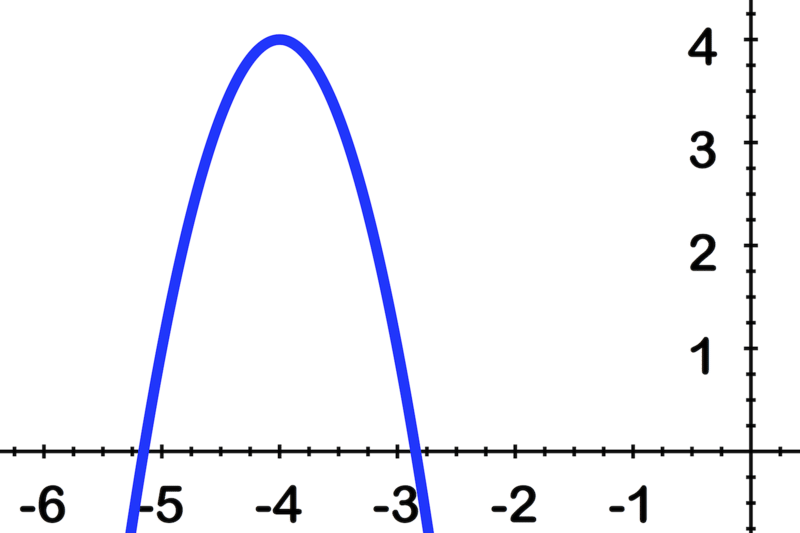
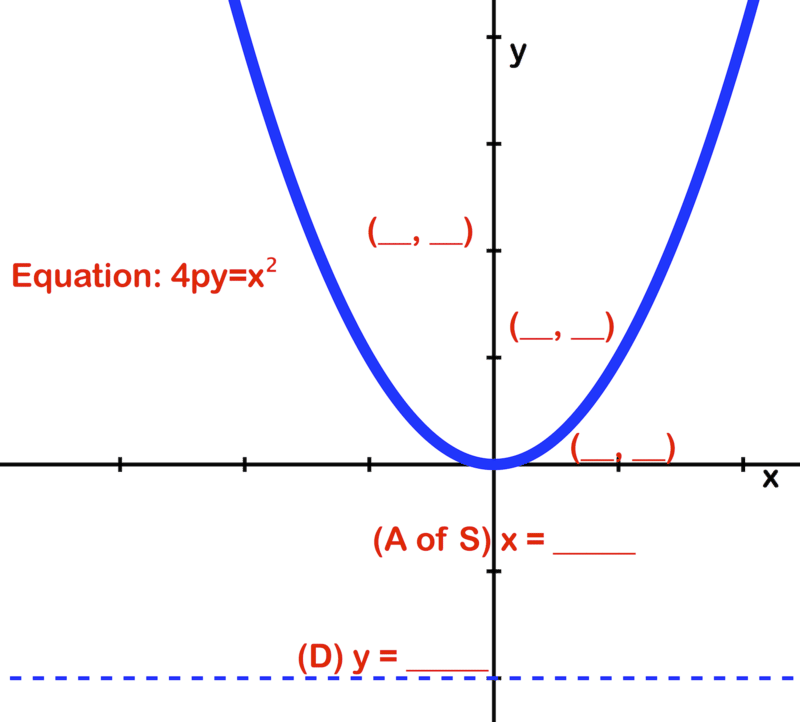
Utilice la imagen y la ecuación dada de la parábola para identificar lo siguiente:

6. Las coordenadas del foco
7. La ecuación de la directrix
8. La longitud del radio focal
9. La ecuación del eje de simetría
10. Las coordenadas del vértice

11. Encuentra la ecuación para una parábola con directrix: x=2 y focus: (0, −2)
12. Encuentra la ecuación para una parábola con vértice: (5, −2) y directriz: y=−5
13. Encuentra la ecuación para una parábola con foco: (3, 5) y vértice: (3, 1)

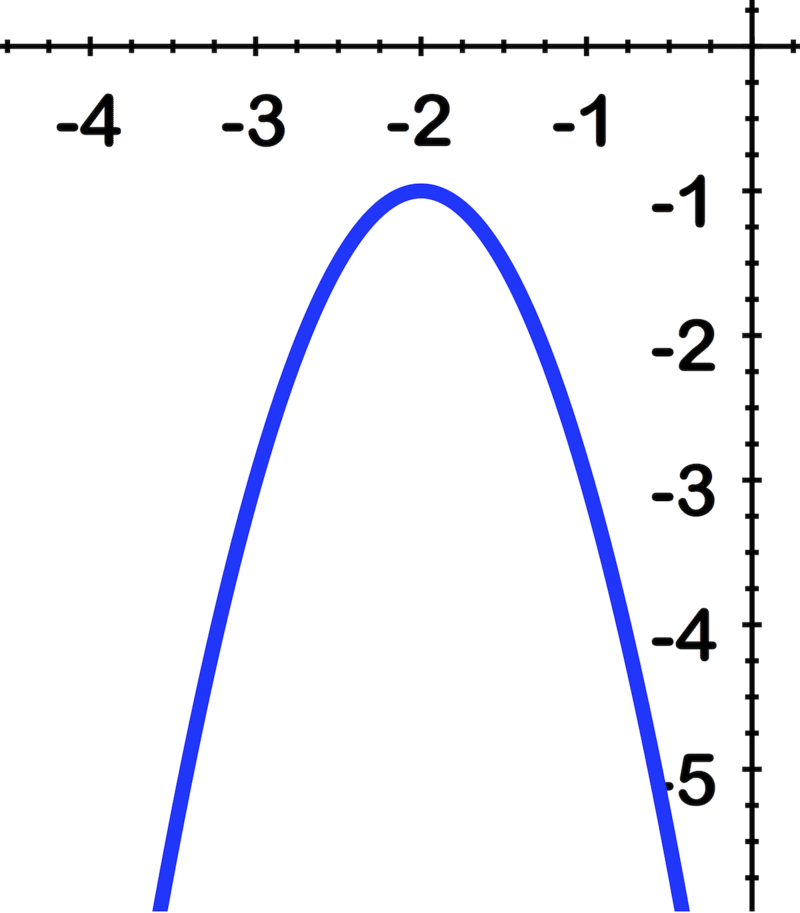
Usa la imagen para identificar el vértice, eje de simetría y ecuación de la parábola:

14. 
15. 
16. 

---

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.4.

---

Recursos

---

El vocabulario

Término	Definición
Geometría Analítica	La geometría analítica es una rama de las matemáticas que se ocupa de modelar y explorar formas mediante el uso de fórmulas algebraicas y un sistema de coordenadas.
eje de simetría	El eje de simetría de una parábola es una línea vertical que pasa por el vértice de la parábola. La parábola es simétrica sobre esta línea.
Cónico	Las secciones cónicas son aquellas curvas que se pueden crear por la intersección de un doble cono y un plano. Incluyen círculos, elipses, parábolas e hipérbolas.
directrix	La directriz de una parábola es la línea de la que parece desviarse la parábola. Todos los puntos en una parábola son equidistantes del foco de la parábola y la directriz de la parábola.
enfoque	El foco de una parábola es el punto que “ancla” una parábola. Cualquier punto de la parábola está exactamente a la misma distancia del foco que de la directriz.
Parábola	Una parábola es el conjunto de puntos que son equidistantes de un punto fijo en el interior de la curva, llamado el “'enfoque"', y una línea en el exterior, llamada la “'directrix"'. La directriz es vertical u horizontal, dependiendo de la orientación de la parábola.