6.3.5: Hipérbolas y asíntotas

Hipérbolas y asíntotas

Al igual que otras secciones cónicas, las hipérbolas se pueden crear “rebanando” un cono y mirando la sección transversal. A diferencia de otras cónicas, las hipérbolas en realidad requieren 2 conos apilados uno encima del otro, punto a punto. La forma es el resultado de crear efectivamente una parábola a partir de ambos conos al mismo tiempo.

Entonces la pregunta es, ¿las hipérbolas deberían considerarse realmente una forma propia? ¿O son solo dos parábolas graficadas al mismo tiempo? ¿Podrían hacerse formas “diferentes” a partir de alguna de las otras secciones cónicas si se usaran dos conos al mismo tiempo?

---

Hipérbolas y asíntotas

Además de su propiedad focal, las hipérbolas también tienen otra propiedad geométrica interesante. A diferencia de una parábola, una hipérbola se acerca infinitesimalmente a una cierta línea a medida que las coordenadas x− o y−se acercan al infinito. ¿Qué queremos decir con “infinitesimalmente cerca”? Aquí nos referimos a dos cosas: 1) Cuanto más vayas a lo largo de la curva, más cerca te acercas a la asíntota, y 2) Si nombras una distancia, por pequeña que sea, eventualmente la curva estará tan cerca de la asíntota. O, usando el lenguaje de los límites, a medida que vamos más lejos del vértice de la hipérbola el límite de la distancia entre la hipérbola y la asíntota es 0.

Estas líneas se llaman asíntotas.

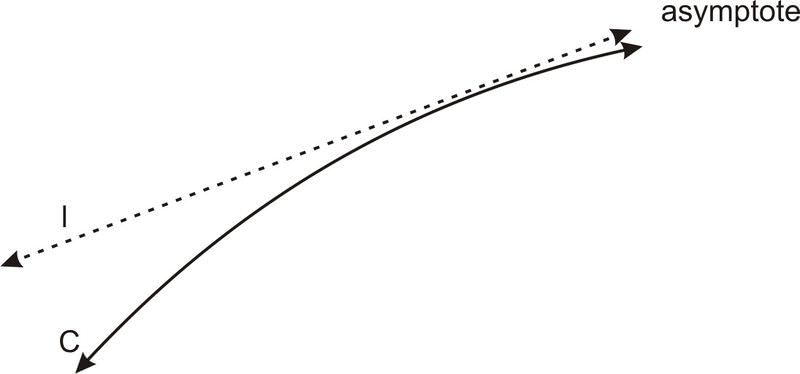
Hay dos asíntotas, y se cruzan en el punto en el que se centra la hipérbola:

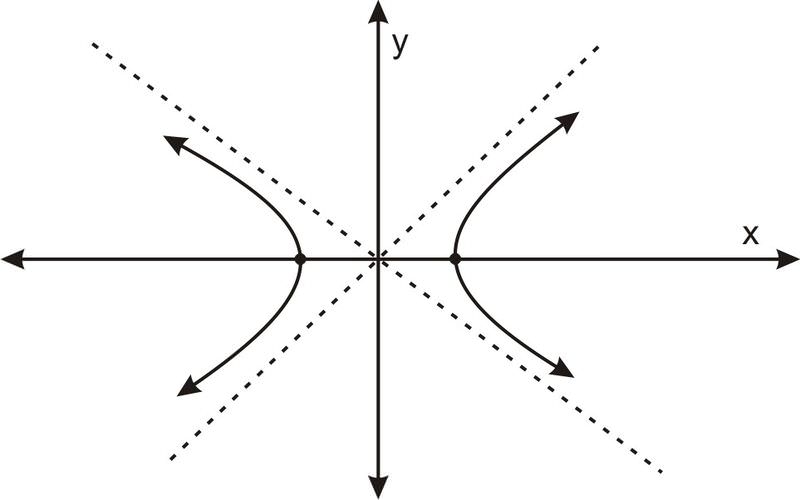
Para una hipérbola de la forma\(\ \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), las asíntotas son las líneas:

\(\ y=\frac{b}{a} x\)y\(\ y=-\frac{b}{a} x\).

Para una hipérbola de la forma\(\ \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\) las asíntotas son las líneas:

\(\ y=\frac{a}{b} x\)y\(\ y=-\frac{a}{b} x\).

(Para una hipérbola desplazada, las asíntotas se desplazan en consecuencia.)

---

Ejemplos

Ejemplo 1

Anteriormente, se le preguntó si las hipérbolas deberían considerarse formas propias.

Solución

Las hipérbolas se consideran formas diferentes, porque existen comportamientos específicos que son exclusivos de las hipérbolas. Además, aunque las hipérbolas son el resultado de parábolas duales, ninguna de las otras cónicas realmente crea formas únicas con conos duales -solo figuras dobles- y en cualquier caso requieren múltiples “rebanadas”.

Ejemplo 2

Grafica la siguiente hipérbola, dibujando sus focos y asíntotas y usándolos para crear un mejor dibujo:\(\ 9 x^{2}-36 x-4 y^{2}-16 y-16=0\)

Solución

Primero, ponemos la hipérbola en la forma estándar:

\ (\\ comenzar {alineado}
9\ izquierda (x^ {2} -4 x\ derecha) -4\ izquierda (y^ {2} +4 y\ derecha) &=16\\
9\ izquierda (x^ {2} -4 x+4\ derecha) -4\ izquierda (y^ {2} +4 y+4\ derecha) &=36\\
\ frac {(x-2) ^ {2}} {4} -\ frac {(y+2) ^ {2}} {9} &=1
\ end {alineado}\)

Entonces\(\ a=2\),\(\ b=3\) y\(\ c=\sqrt{4+9}=\sqrt{13}\). La hipérbola está orientada horizontalmente, centrada en el punto\(\ (2,-2)\), con focos en\(\ (2+\sqrt{13},-2)\) y\(\ (2-\sqrt{13},-2)\). Después de tomar en consideración el cambio, las asíntotas son las líneas:\(\ y+2=\frac{3}{2}(x-2)\) y\(\ y+2=-\frac{3}{2}(x-2)\). Entonces graficando los vértices y algunos puntos a cada lado, vemos que la hipérbola se ve algo así:

Ejemplo 3

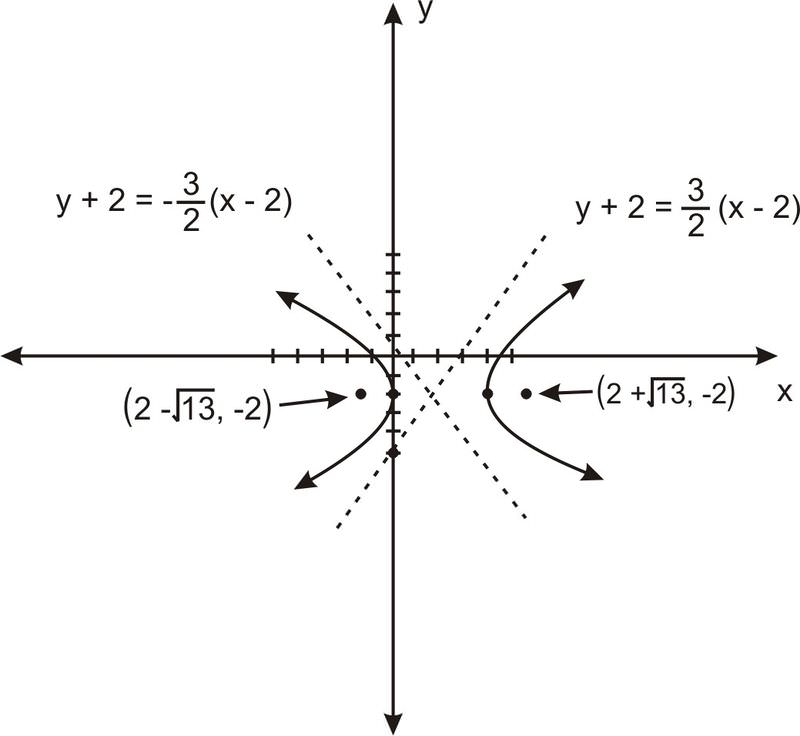
Grafica la siguiente hipérbola, dibujando sus focos y asíntotas y usándolos para crear un mejor dibujo:\(\ 16 x^{2}-96 x-9 y^{2}-36 y-84=0\)

Solución

Ejemplo 4

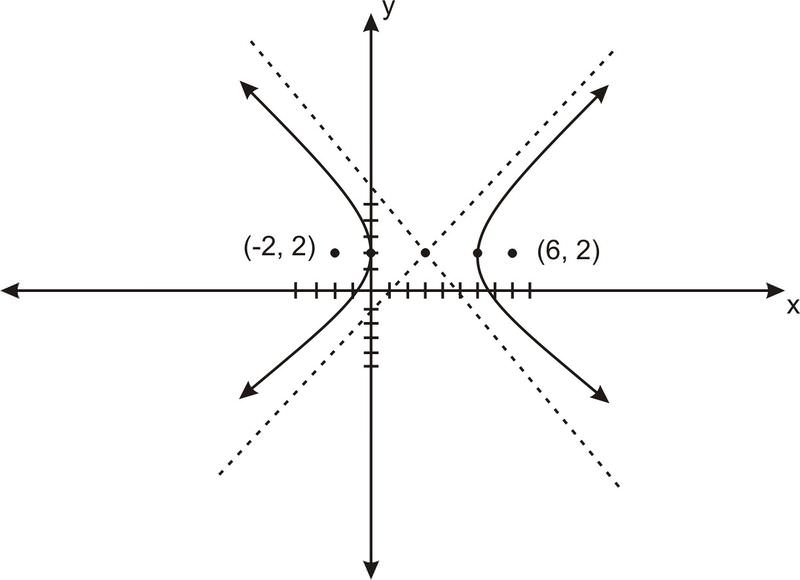
Grafica la siguiente hipérbola, dibujando sus focos y asíntotas, y úsalos para crear un mejor dibujo:\(\ y^{2}-14 y-25 x^{2}-200 x-376=0\).

Solución

Ejemplo 5

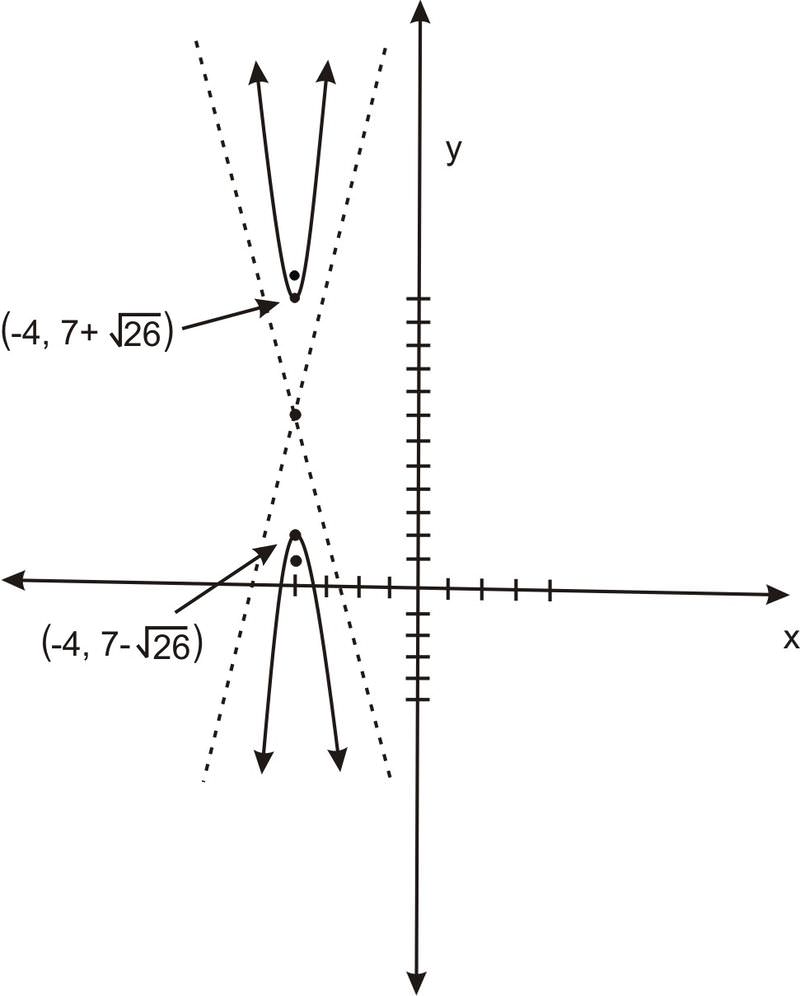
Encuentra la ecuación para una hipérbola con asíntotas de pendientes\(\ \frac{5}{12}\) y\(\ -\frac{5}{12}\), y focos en puntos\(\ (2,11)\) y\(\ (2,1)\).

Solución

\(\ \frac{(y-6)^{2}}{25}-\frac{(x-2)^{2}}{144}=1\)

Ejemplo 6

Una hipérbola con asíntotas perpendiculares se llama perpendicular. ¿Qué aspecto tiene la ecuación de una hipérbola perpendicular?

Solución

Las pendientes de las líneas perpendiculares son recíprocas negativas entre sí. Esto significa eso\(\ \frac{a}{b}=\frac{b}{a}\), que, para positivo\(\ a\) y\(\ b\) significa\(\ a=b\).

Ejemplo 7

Encuentra una ecuación de la hipérbola con intercepciones x en\(\ x = –7\) y\(\ x = 5\), y focos en\(\ (–6, 0)\) y\(\ (4, 0)\).

Solución

Los focos tienen las mismas coordenadas y, por lo que esta es una hipérbola izquierda/derecha con el centro, focos y vértices en una línea paralela al eje x.

Al tratarse de una hipérbola izquierda/derecha, la parte y de la ecuación será negativa y la ecuación conducirá con el\(\ x^{2}\) término (ya que el término principal es positivo por convención y el término cuadrado debe tener signos diferentes si se trata de una hipérbola).: El centro está a medio camino entre los focos, por lo que el centro \(\ (h, k)=(-1,0)\). Los focos c son 5 unidades a cada lado del centro, así que\(\ c=5 \rightarrow c^{2}=25\).

Las intercepciones x son 4 unidades a cada lado del centro, y los focos están en el eje x por lo que las intercepciones deben ser los vértices\(\ a\)\(\ a=4 \rightarrow a^{2}=16\).

Usa el teorema de Pitágoras,\(\ a^{2}+b^{2}=c^{2}\), para obtener\(\ b^{2}=25-16=9\).

Sustituir los valores calculados en la forma estándar\(\ \frac{(x-h)^{2}}{a}-\frac{(y-k)^{2}}{b}=1\) para obtener\(\ \frac{(x+1)^{2}}{16}-\frac{y^{2}}{9}=1\).

---

Revisar

Encuentra las ecuaciones de las asíntotas de cada hipérbola.

1. \(\ \frac{(y+3)^{2}}{4}-(x-2)^{2}=1\)
2. \(\ \frac{y^{2}}{16}-(x+3)^{2}=1\)
3. \(\ \frac{(x+2)^{2}}{4}-\frac{(y+1)^{2}}{9}=1\)
4. \(\ \frac{(y-4)^{2}}{16}-\frac{(x-4)^{2}}{16}=1\)
5. \(\ \frac{(x-1)^{2}}{1}-\frac{9(y+4)^{2}}{1}=9\)
6. \(\ \frac{(y+2)^{2}}{16}-\frac{(x-2)^{2}}{1}=1\)
7. \(\ \frac{(x-4)^{2}}{1}-\frac{(y+1)^{2}}{4}=1\)
8. \(\ \frac{y^{2}}{16}-\frac{(x+1)^{2}}{4}=1\)
9. \(\ \frac{(x-3)^{2}}{4}-\frac{(y-4)^{2}}{1}=1\)
10. \(\ \frac{(x-4)^{2}}{4}-\frac{(y-3)^{2}}{1}=1\)

Grafica las hipérbolas, da la ecuación de las asíntotas y usa las asíntotas para mejorar la precisión de tu gráfica.

11. \(\ \frac{(x+4)^{2}}{4}-\frac{(y-1)^{2}}{9}=1\)
12. \(\ \frac{(y+3)^{2}}{4}-\frac{(x-4)^{2}}{9}=1\)
13. \(\ \frac{(y+4)^{2}}{16}-\frac{(x-1)^{2}}{4}=1\)
14. \(\ (x-2)^{2}-4 y^{2}=16\)
15. \(\ \frac{y^{2}}{4}-\frac{(x-1)^{2}}{4}=1\)
16. \(\ \frac{(x-2)^{2}}{16}-\frac{(y+4)^{2}}{1}=1\)
17. \(\ \frac{(x+2)^{2}}{9}-\frac{(y+2)^{2}}{16}=1\)
18. \(\ \frac{(x+4)^{2}}{9}-\frac{(y-2)^{2}}{4}=1\)

---

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.7.

---

vocabulario

Término	Definición
asíntotas	Una asíntota es una línea en la gráfica de una función que representa un valor hacia el que la función puede acercarse, pero no alcanza (con ciertas excepciones).
Cónico	Las secciones cónicas son aquellas curvas que se pueden crear por la intersección de un doble cono y un plano. Incluyen círculos, elipses, parábolas e hipérbolas.
hipérbola	Una hipérbola es una sección cónica formada cuando el plano de corte cruza ambos lados del cono, dando como resultado dos curvas infinitas en forma de “U”.
Parábola	Una parábola es el conjunto de puntos que son equidistantes de un punto fijo en el interior de la curva, llamado el “'foco"', y una línea en el exterior, llamada la “'directrix"'. La directriz es vertical u horizontal, dependiendo de la orientación de la parábola.
hipérbola perpendicular	Una hipérbola perpendicular tiene asíntotas que se cruzan en un ángulo de 90°.
sin límites	Estar sin límites significa ser tan grande que ningún círculo, por más grande que sea, puede encerrar la forma.