6.5.4: Resolver sistemas de líneas, cuadráticas y cónicas
- Page ID
- 108852
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Resolviendo sistemas de líneas, cuadráticas y cónicas
Se te da la elipse\(\ \frac{x^{2}}{4}+\frac{y^{2}}{9}=1\) y la línea\(\ y=\frac{3}{2} x+3\). Se quiere determinar en qué punto (s), si los hay, las dos ecuaciones se cruzan sin graficar. ¿La línea se intersecta con la elipse? Si es así, ¿en qué punto (s) lo hace?
Sistemas de Líneas, Cuadráticas y Cónicas
Anteriormente, resolvimos un sistema que involucraba dos líneas o tres planos, mediante el uso de gráficos, sustitución y combinaciones lineales. En este concepto, agregaremos círculos, parábolas y elipses a los sistemas de ecuaciones. Debido a que tanto x como y pueden estar al cuadrado en estas ecuaciones, a menudo habrá más de una respuesta.
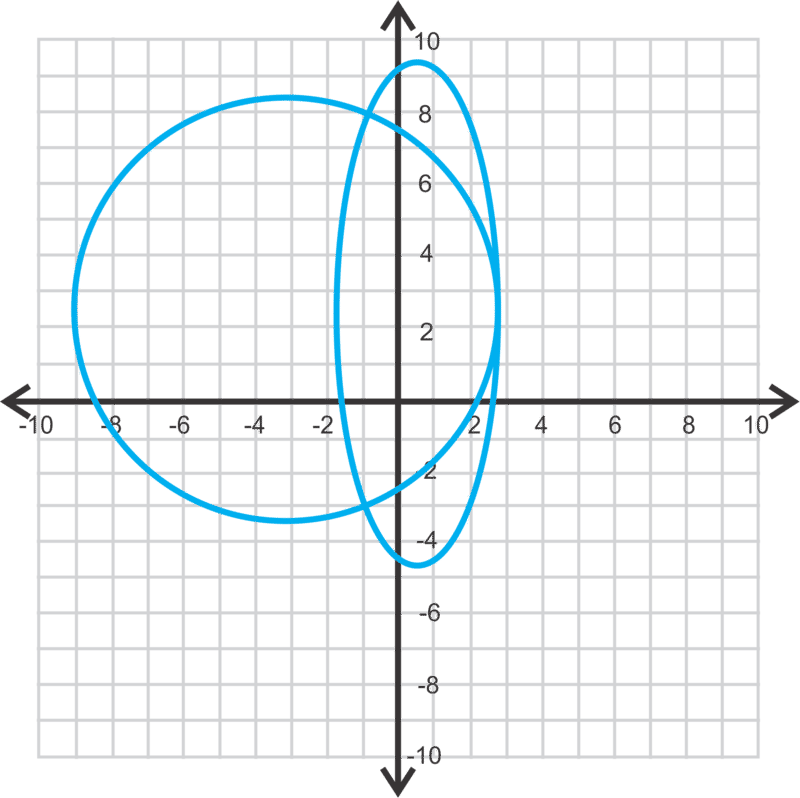
Estimemos las soluciones para el sistema de ecuaciones a continuación.
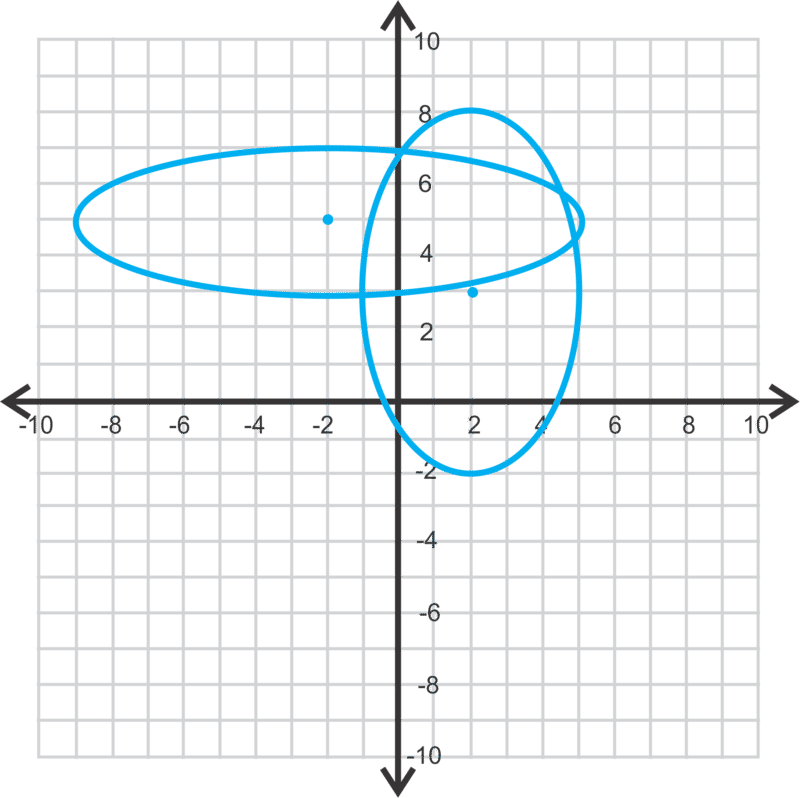
Estas dos elipses se cruzan en cuatro lugares. Parecen ser los siguientes puntos:
(0, 7), (4.7, 5.5), (4.9, 4.3) y (−1, 2.9)
Ten en cuenta que estas son solo estimaciones. En el siguiente problema, mostraremos cómo encontrar las respuestas exactas.
Ahora, vamos a resolver
\ (\\ begin {array} {l}
x^ {2} +y^ {2} =25\\
3 x+2 y=6
\ end {array}\)
Resolvamos este sistema graficando. La primera ecuación es un círculo, centrado en el origen, con un radio de 5. La segunda ecuación es una línea. En forma de intercepción de pendiente, es\(\ y=-\frac{3}{2} x+3\).
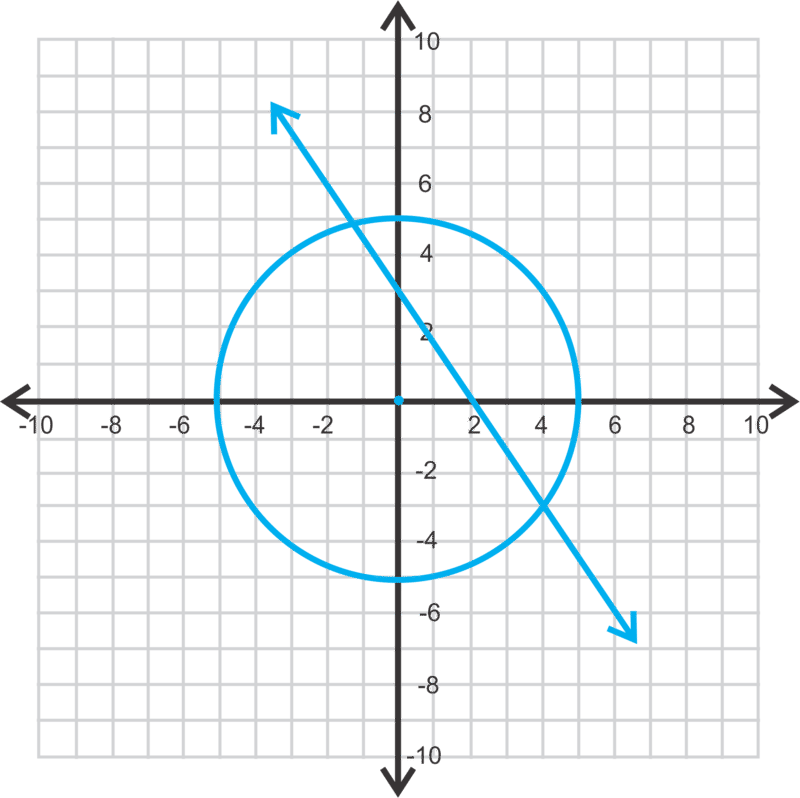
A continuación, calculemos dónde se cruzan la línea y el círculo. En el segundo cuadrante, se ve como (−1.2, 4.8) y en el cuarto cuadrante se ve como (4, −3). Estas son nuestras respuestas estimadas.
Para encontrar el valor exacto de estos puntos de intersección, necesitamos usar la sustitución. Sustituir en la ecuación lineal en para y en la ecuación de círculo y resolver para x.
\ (\\ comenzar {alineado}
x^ {2} +\ izquierda (-\ frac {3} {2} x+3\ derecha) ^ {2} &=25\\
x^ {2} +\ frac {9} {4} x^ {2} -9 x+9 &=25\
\ frac {13} {4} x^ {2} -9 x-16 &=0\
13 x^ {2} -36 x-64 &=0
\ final {alineado}\)
Utilice la fórmula cuadrática:
\ (\\ comenzar {alineado}
x &=\ frac {36\ pm\ sqrt {36^ {2} -4 (13) (-64)}} {2 (13)}}\\
&=\ frac {36\ pm\ sqrt {4624}} {26}\\
&=\ frac {36\ pm 68} {26}
\ end {alineado}\)
Las soluciones, para x, son\(\ \frac{36+68}{26}=4\) y\(\ \frac{36-68}{26}=-1 \frac{3}{13}\). Conecte estos en cualquiera de las ecuaciones para resolver para y.
\(\ y=-\frac{3}{2}(4)+3=-3\)y\(\ y=-\frac{3}{2}\left(-\frac{16}{13}\right)+3=4 \frac{11}{13}\)
Los puntos son (4, −3) y\(\ \left(-1 \frac{3}{13}, 4 \frac{11}{13}\right)\).
La técnica utilizada en este problema es cómo se recomienda que abordes cada problema. Primero, grafica el sistema para que tengas una idea de cuántas soluciones hay y dónde se encuentran. Entonces, usa la sustitución para resolver las respuestas exactas.
Por último, vamos a resolver
\ (\\ begin {array} {l}
\ frac {x^ {2}} {16} +\ frac {y^ {2}} {9} =1\\
y^ {2} =-\ frac {4} {3} (x-6)
\ end {array}\)
Graficando las dos ecuaciones, tenemos cuatro puntos de intersección abajo. La segunda ecuación se resuelve para\(\ y^{2}\), así que sustituya eso en la primera ecuación.
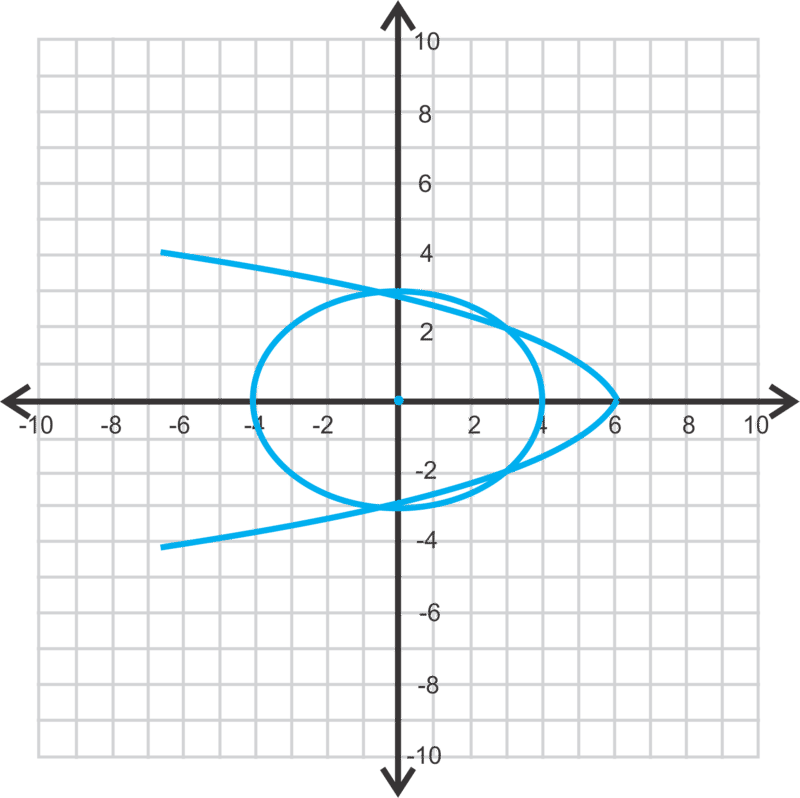
\ (\\ comenzar {alineado}
\ frac {x^ {2}} {16} -\ frac {4 (x-6)} {3\ cdot 9} &=1\\
\ frac {x^ {2}} {16} -\ frac {4 x-24} {27} &=1\\
27 x^ {2} -16 (4 x-24) &=432\
27 x^ {2} -64 x-48 &=0
\ end {alineado}\)
Ahora, usa la Fórmula Cuadrática para resolver x.
\ (\\ begin {alineado}
x &=\ frac {64\ pm\ sqrt {(-64) ^ {2} -4 (27) (-48)}} {2 (27)}\\
&=\ frac {64\ pm\ sqrt {9280}} {54}\
&=\ frac {32\ pm 4\ sqrt {145}} {27}
\ final {alineado}\)
Conectando estos a la calculadora que obtenemos\(\ x=\frac{32+4 \sqrt{145}}{27} \approx 2.97\) y\(\ x=\frac{32-4 \sqrt{145}}{27} \approx-0.6\). Al mirar la gráfica, sabemos que habrá dos valores y diferentes para cada valor x para dar cuatro puntos de intersección. Usando las estimaciones, resuelve para y. Puedes elegir cualquiera de las ecuaciones.
\ (\\ begin {array} {rlrl}
y^ {2} & =-\ frac {4} {3} (2.97-6) & y^ {2} &=-\ frac {4} {3} (-0.6-6)\\
y^ {2} & =4.04 &\ text {and} & y^ {2} & =8.8\\
y & =\ pm 2.01 && y & =\ pm 2.97
\ end {array}\)
Los puntos son (2.97, 2.01), (2.97, −2.01), (−0.6, 2.97), y (−0.6, −2.97).
Ejemplos
Anteriormente, se le pidió que determinara si la línea se\(\ y=\frac{3}{2} x+3\) cruza con la elipse\(\ \frac{x^{2}}{4}+\frac{y^{2}}{9}=1\), y de ser así, en qué punto (s).
Solución
Primero, deshagamos de las fracciones en la ecuación de la elipse para que sea más fácil trabajar con ellas. Para ello, multiplicamos por la LCD.
\ (\\ begin {array} {r}
\ frac {x^ {2}} {4} +\ frac {y^ {2}} {9} =1\
36\ frac {x^ {2}} {4} +36\ frac {y^ {2}} {9} =36\ cdot 1\
9 x^ {2} +4 y^ {2} =36
\ fin {matriz}\)
Ahora podemos sustituir la ecuación de la línea\(\ y=\frac{3}{2} x+3\) en por y y resolver por x.
\ (\\ comenzar {matriz} {r}
9 x^ {2} +4\ izquierda (\ frac {3} {2} x+3\ derecha) ^ {2} =36\\
9 x^ {2} +4\ izquierda (\ frac {9} {4} x^ {2} +9 x+9\ derecha) =36\\
9 x^ {2} +9 x^ {2} +36 x+36=36\\
18 x^ {2} +36 x=0\\
18 x (x+2) =0
\ end {array}\)
Entonces,\(\ x=0\) o\(\ x=−2\)
Finalmente podemos sustituir estos valores x en la ecuación de la línea para encontrar los valores y correspondientes.
\ (\\ begin {array} {l}
y=\ frac {3} {2} (0) +3=3\\
y=\ frac {3} {2} (-2) +3=0
\ end {array}\)
Por lo tanto, la línea se cruza con la elipse en puntos\(\ (0, 3)\) y\(\ (−2, 0)\).
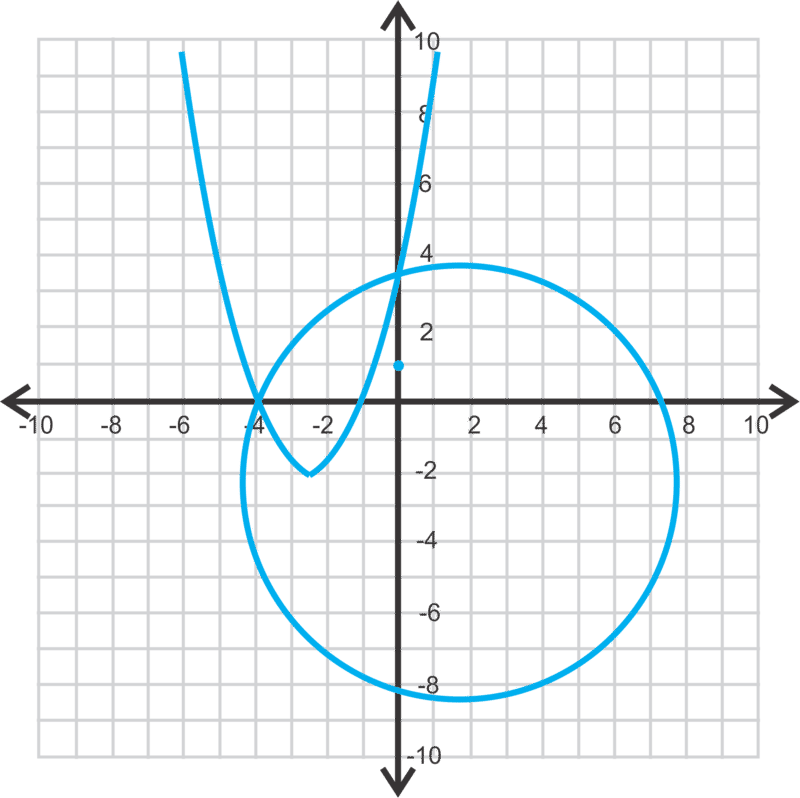
Estime las soluciones al sistema a continuación.
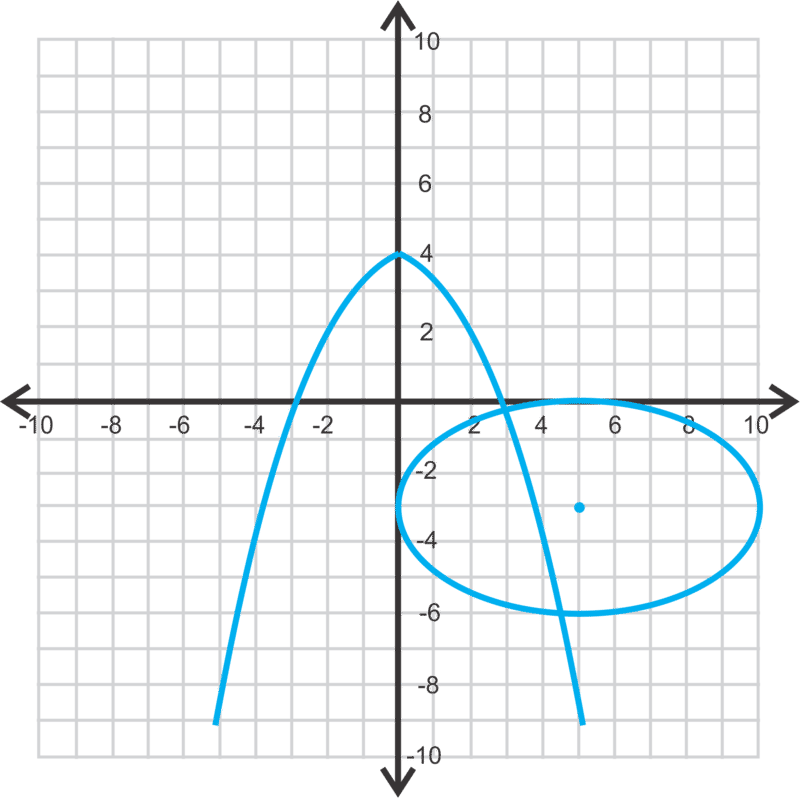
Solución
(3, −0.1) y (4.5, −6)
Encuentre las soluciones a los sistemas a continuación.
\ (\\ comenzar {alineado}
x^ {2} + (y-1) ^ {2} &=36\\
x^ {2} &=2 (y+9)
\ end {alineado}\)
Solución
Se trata de un círculo y una parábola que se cruza en cuatro lugares.
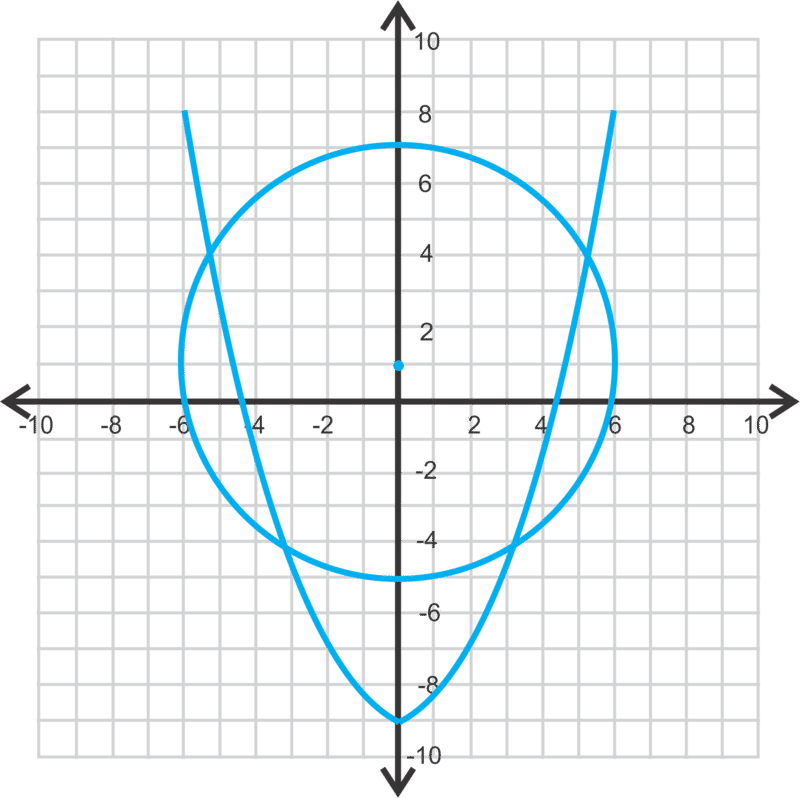
Usando la sustitución para\(\ x^{2}\), tenemos:
\ (\\ comenzar {alineado}
2 (y+9) + (y-1) ^ {2} &=36\\
2 y+18+y^ {2} -2 y+1 &=36\\
y^ {2} &=17\\
y &=\ pm\ sqrt {17}\ approx\ pm 4.12
\ final {alineado}\)
Los valores x correspondientes son:
\ (\\ begin {alineado}
x^ {2} &=2 (4.12+9) & x^ {2} &=2 (-4.12+9)\\
x^ {2} &=26.25\ quad\ quad\ quad\ quad\ quad\ text {y} & x^ {2} &=9.76\\
x &=\ pm 5.12 & x&=\ pm 3.12
\ end {alineado}\)
Las soluciones son: (4.12, 5.12), (4.12, −5.12), (−4.12, 3.12) y (−4.12, −3.12).
\ (\\ comenzar {alineado}
x^ {2} &=y+8\\
4 x+5 y &=12
\ final {alineado}\)
Solución
Se trata de una línea y una parábola que se cruzan en dos puntos.
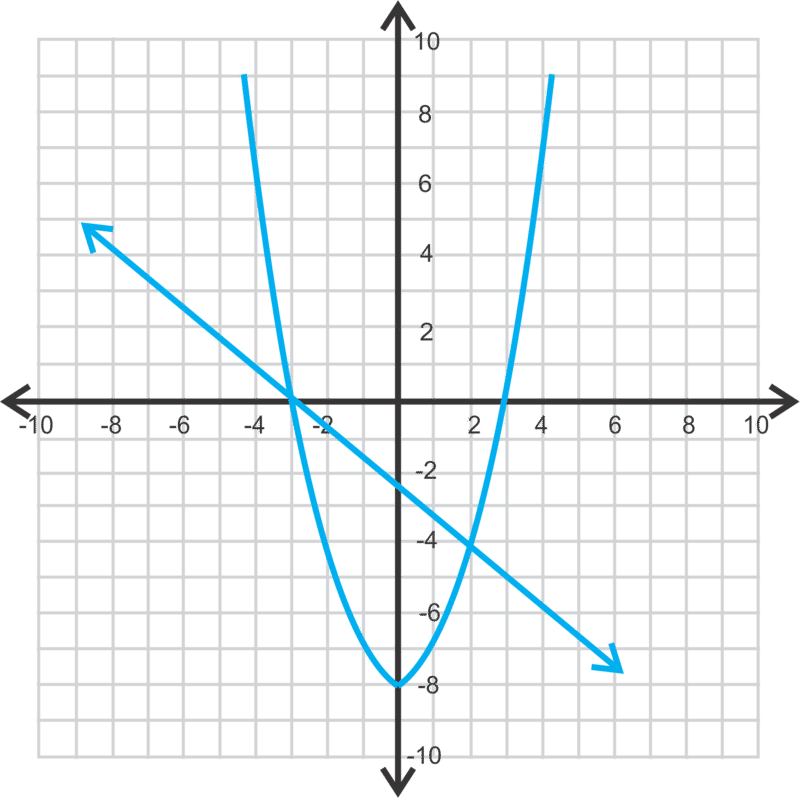
Resolver la primera ecuación para y y sustituir en la segunda.
\ (\\ comenzar {alineado}
4 x+5\ izquierda (x^ {2} -8\ derecha) &=12\\
4 x+5 x^ {2} -40 &=12\\
5 x^ {2} +4 x-52 &=0\\
x &=\ frac {-4\ pm\ sqrt {4^ {2} -4 (5) (-52)}} {2 (5)}\\
x &=\ frac {-4\ pm\ sqrt {1056}} {10}\ aproximadamente 3.65,2.85
\ fin {alineado}\)
Usando la primera ecuación,\(\ y=3.65^{2}-8=5.32\) y\(\ y=2.85^{2}-8=0.12\). Los puntos son\(\ (3.65,5.32)\) y\(\ (2.85,0.12)\).
Revisar
Estime las soluciones para cada sistema de ecuaciones a continuación.
Resuelve cada sistema de ecuaciones a continuación.
- \ (\\ comenzar {alineado}
5 x^ {2} +3 y &=17\\
x-y &=1
\ final {alineado}\) - \ (\\ begin {array} {c}
x^ {2} +y^ {2} =7.5\\
x+2 y=6
\ end {array}\) - \ (\\ begin {alineado}
x^ {2} &=y+4\\
\ frac {x^ {2}} {4} + (y+2) ^ {2} &=1
\ end {alineado}\) - \ (\\ begin {alineado}
(x-1) ^ {2} + (y-3) ^ {2} &=25\\
x^ {2} &=-2 (y-10)
\ end {alineado}\) - \ (\\ begin {array} {l}
x^ {2} +y^ {2} =16\\
4 x-3 y=18
\ end {array}\) - \ (\\ begin {alineado}
(x+4) ^ {2} + (y+1) ^ {2} &=36\\
\ frac {(x+1) ^ {2}} {4} +\ frac {(y-2) ^ {2}} {25} &=1
\ end {alineado}\) - ¿Cuántas formas diferentes pueden cruzarse un círculo y una parábola? Dibuja cada posibilidad.
- ¿Cuántas formas diferentes pueden cruzarse un círculo y una elipse? Dibuja cada posibilidad.
- Crea un sistema de dos círculos sin solución. ¿Cómo sería la gráfica?
- Desafío Encuentra las soluciones para el sistema
\ (\\ comenzar {alineado}
x^ {2} +y^ {2} &=r^ {2}\\
y &=m x
\ final {alineado}\)
Deja tus respuestas en términos de\(\ m\) y\(\ r\).
- Desafío Determinar si el sistema de tres ecuaciones a continuación tiene una solución común.
\ (\\ comenzar {alineado}
x^ {2} +3 y^ {2} &=16\\
3 x^ {2} +y^ {2} &=16\\
y &=x
\ end {alineado}\)
Respuestas para problemas de revisión
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.12.
Atribuciones de imagen
- [Figura 1]
Fuente: https://www.flickr.com/photos/76657755@N04/7067719845/in/photolist-bLxUSH-cEQdcG-sqcQh3-dnQDJC-SFo7H2-TojZMy-RCLLRv-SCJrjE-ShVoJ5-SSLaXc-SFqf7X-ShMjEQ-SSCQxz-SCS1fW-SCRxjm-RA8CDA-SCVo7W-RAgWYL-RCLTpR-RCFkKP-SCUQrb-RCLfoM-RA9k9U-ShMPey - Snzlpw-ssk11r-shn1b3-spbdj3-rae5ug-sp36gm-sd2skp-sp6zpm-rcfit2-sslrt2-scwgjd-shmpm3-sshmlx-shdfrf-sczafa-rclj6v-r3va3w-rcjkjh-shr7dy-rcgmu2-spbkvw-ra7hwg-UGC-RCFESG-JJOUQN-DHPRCR; https://www.flickr.com/photos/miwok/27224730280/