8.1.2: Límites unilaterales
- Page ID
- 108717
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Límites y continuidad de un solo lado
Un límite unilateral es exactamente lo que podría esperar; el límite de una función a medida que se acerca a un\(\ x\) valor específico ya sea desde el lado derecho o desde el lado izquierdo. Los límites unilaterales ayudan a lidiar con el tema de una discontinuidad de salto y los dos lados no coinciden.
¿La siguiente función por partes es continua?
\ (\ f (x) =\ left\ {\ begin {array} {cc}
-x-2 & x<1\\
-3 & x=1\\
x^ {2} -4 & 1<x
\ end {array}\ derecha.\)
Evaluación de límites unilaterales y continuidad
Un límite unilateral se puede evaluar ya sea desde la izquierda o desde la derecha. Dado que la izquierda y la derecha no son direcciones absolutas, una forma más precisa de pensar la dirección es “desde el lado negativo” o “desde el lado positivo”. La notación para estos límites unilaterales es:
\(\ \lim _{x \rightarrow a^{-}} f(x), \lim _{x \rightarrow a^{+}} f(x)\)
El negativo en el superíndice de no\(\ a\) es un exponente. En cambio indica desde el lado negativo. De igual manera el superíndice positivo no es un exponente, solo significa desde el lado positivo. Al evaluar límites unilaterales, no importa lo que esté haciendo la función en el punto real o lo que la función esté haciendo en el otro lado del número. Tu trabajo es determinar cuál debe ser la altura de la función usando solo evidencia por un lado.
Toma la gráfica a continuación. ¿Cuáles son los límites unilaterales en -5, -1, 3 y 5?
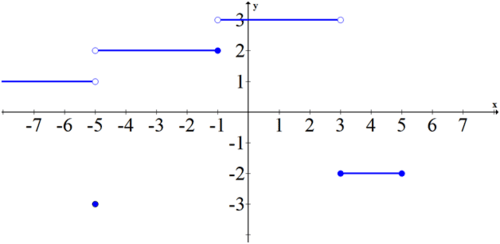
Cada punto debe tener dos límites, uno desde la izquierda y otro desde la derecha.
\ (\\ begin {array} {ll}
\ lim _ {x\ fila derecha-5^ {-}} f (x) &=1\ cuádruple\ cuádruple\ cuádruple\ cuádruple\ cuádruple\ cuádruple\ lim _ {x\ fila derecha-5^ {+}} f (x) &=2
\\ lim _ {x\ fila derecha-1^ {-}} f (x) &=2 &\ lim _ {x\ fila derecha-1^ {+}} f (x) &=3\
\\ lim _ {x\ fila derecha 3^ {-}} f (x) &=3 &\ lim _ {x\ fila derecha 3^ {+}} f (x) &=-2\\
\ lim _ {x\ fila derecha 5^ {-}} f (x) &=-2 &\ lim _ {x\ fila derecha-5^ {+}} f (x) &=D N E
\ end {array}\)
Has definido la continuidad en el pasado como la capacidad de dibujar una función completamente sin levantar tu lápiz del papel. Ahora se puede definir una definición más rigurosa de continuidad.
La continuidad en un punto existe cuando los límites de los lados izquierdo y derecho coinciden con la función evaluada en ese punto. En otras palabras, una función es continua en\(\ a\) si:
\(\ \lim _{x \rightarrow a^{-}} f(x)=f(a)=\lim _{x \rightarrow a^{+}} f(x)\)
Para que toda una función sea continua, la función debe ser continua en cada punto de un dominio ininterrumpido.
Ejemplos
Anteriormente, le preguntaron cómo confirmar la función
\ (\ f (x) =\ left\ {\ begin {array} {cc}
-x-2 & x<1\\
-3 & x=1\\
x^ {2} -4 & 1<x
\ end {array}\ derecha.\)
Solución
es continuo. Para confirmar o negar que la función es continua, las herramientas gráficas no son lo suficientemente precisas. A veces las discontinuidades de salto pueden estar apagadas en una cantidad tan pequeña que los píxeles en la pantalla de su calculadora no mostrarán una diferencia. Su calculadora ciertamente no mostrará discontinuidades removibles.
Debes tener en cuenta que en la gráfica, todo a la izquierda de 1 es continuo porque es solo una línea. A continuación hay que señalar que todo a la derecha de 1 también es continuo por la misma razón. El único punto a verificar es en\(\ x=1\). Para verificar la continuidad, use explícitamente la definición y evalúe las tres partes para ver si son iguales.
- \(\ \lim _{x \rightarrow a^{-}} f(x)=-1-2=-3\)
- \(\ f(1)=-3\)
- \(\ \lim _{x \rightarrow 1^{+}} f(x)=1^{2}-4=-3\)
Por lo tanto,\(\ \lim _{x \rightarrow 1^{-}} f(x)=f(1)=\lim _{x \rightarrow 1^{+}} f(x)\) y la función es continua en\(\ x=1\) y en todas partes.
Evaluar numéricamente el límite unilateral a 4 desde la dirección negativa.
\(\ f(x)=\frac{x^{2}-7 x+12}{x-4}\)
Solución
Recuerda que evaluar numéricamente significa que debes usar una tabla. Al crear la tabla, solo use valores que sean menores a 4.
| x | 3.9 | 3.99 | 3.999 |
| f (x) | 0.9 | 0.99 | 0.999 |
\(\ \lim _{x \rightarrow 4^{-}}\left(\frac{x^{2}-7 x+12}{x-4}\right)=1\)
Evaluar los siguientes límites.
- \(\ \lim _{x \rightarrow 3^{-}}(4 x-3)\)
- \(\ \lim _{x \rightarrow 2^{+}}\left(\frac{1}{x-2}\right)\)
- \(\ \lim _{x \rightarrow 1^{+}}\left(\frac{x^{2}+2 x-3}{x-1}\right)\)
Solución
La mayoría de las veces los límites unilaterales son los mismos que el límite de dos lados correspondiente. Las excepciones son cuando hay discontinuidades de salto, que normalmente solo ocurren con funciones por partes, y discontinuidades infinitas, que normalmente solo ocurren con funciones racionales.
- \(\ \lim _{x \rightarrow 3^{-}}(4 x-3)=4 \cdot 3-3=12-3=9\)
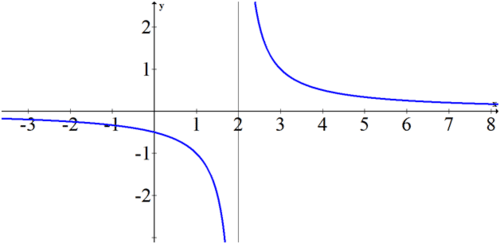
- \(\ \lim _{x \rightarrow 2^{+}}\left(\frac{1}{x-2}\right)=D N E \text { or } \infty\)
La razón por la que ∞ es preferible en este caso es porque los dos lados del límite no están de acuerdo. Un lado va al infinito negativo y el otro lado va al infinito positivo (ver la gráfica a continuación). Si solo indicas DNE entonces estás perdiendo alguna información perfectamente buena sobre la naturaleza de la función.
- \(\ \lim _{x \rightarrow 1^{+}}\left(\frac{x^{2}+2 x-3}{x-1}\right)=\lim _{x \rightarrow 1^{+}}\left(\frac{(x-1)(x+3)}{(x-1)}\right)=\lim _{x \rightarrow 1^{+}}(x+3)=1+3=4\)
Evaluar los siguientes límites.
- \(\ \lim _{x \rightarrow 1^{-}}(2 x-1)\)
- \(\ \lim _{x \rightarrow-3^{+}}\left(\frac{2}{x+2}\right)\)
- \(\ \lim _{x \rightarrow 2^{+}}\left(\frac{x^{3}-8}{x-2}\right)\)
Solución
- \(\ \lim _{x \rightarrow 1^{-}}(2 x-1)=2 \cdot 1-1=2-1=1\)
- \(\ \lim _{x \rightarrow-3^{+}}\left(\frac{2}{x+2}\right)=\frac{2}{-3+2}=\frac{2}{-1}=-2\)
¿La siguiente función es continua?
\ (\ f (x) =\ left\ {\ begin {array} {cc}
x^ {2} -1 & x<-1\\
3 & x=-1\
-x+3 & -1<x
\ end {array}\ derecha.\)
Solución
Utilizar la definición de continuidad.
- \(\ \lim _{x \rightarrow 1^{-}} f(x)=(-1)^{2}-1=1-1=0\)
- \(\ f(-1)=3\)
- \(\ \lim _{x \rightarrow-1^{+}} f(x)=-1+3=2\)
\(\ \lim _{x \rightarrow a^{-}} f(x) \neq f(a) \neq \lim _{x \rightarrow a^{+}} f(x)\)por lo que esta función es discontinua en\(\ x=−1\). Es continuo en todas partes.
Revisar
Evaluar los siguientes límites.
- \(\ \lim _{x \rightarrow 6^{-}}\left(3 x^{2}-4\right)\)
- \(\ \lim _{x \rightarrow 0^{-}} \frac{3 x-1}{x}\)
- \(\ \lim _{x \rightarrow 0^{+}} \frac{3 x-1}{x}\)
- \(\ \lim _{x \rightarrow 0^{+}} \frac{x}{|x|}\)
- \(\ \lim _{x \rightarrow 0^{-}} \frac{x}{|x|}\)
- \(\ \lim _{x \rightarrow 0^{+}} \frac{\sqrt{x}}{\sqrt{1+\sqrt{x}}-1}\)
Considerar
\ (\ f (x) =\ left\ {\ begin {array} {cc}
2 x^ {2} -1 & x<1\\
1 & x=1\\
-x+2 & 1<x
\ end {array}\ derecha.\)
- ¿Qué es\(\ \lim _{x \rightarrow 1^{-}} f(x)\)?
- ¿Qué es\(\ \lim _{x \rightarrow 1^{+}} f(x)\)?
- ¿Es\(\ f(x)\) continuo en\(\ x=1\)?
Considerar
\ (\ g (x) =\ left\ {\ begin {array} {cl}
4 x^ {2} +2 x-1 & x<-2\\
8 & x=-2\\
-3 x+5 & -2<x
\ end {array}\ derecha.\)
- ¿Qué es\(\ \lim _{x \rightarrow-2^{-}} g(x)\)?
- ¿Qué es\(\ \lim _{x \rightarrow-2^{+}} g(x)\)?
- ¿Es\(\ g(x)\) continuo en\(\ x=-2\)?
Considera que\(\ h(x)\) se muestra en la gráfica a continuación.
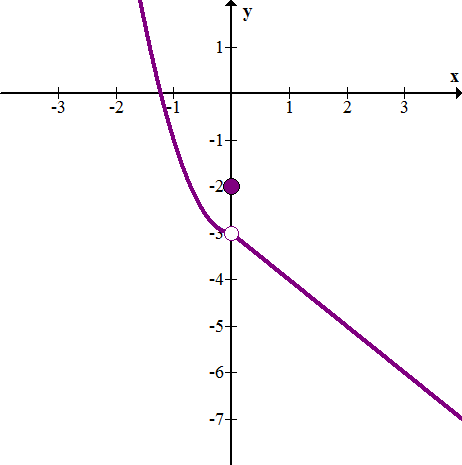
- ¿Qué es\(\ \lim _{x \rightarrow 0^{-}} h(x)\)?
- ¿Qué es\(\ \lim _{x \rightarrow 0^{+}} h(x)\)?
- ¿Es\(\ h(x)\) continuo en\(\ x=0\)?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 14.6.
El vocabulario
| Término | Definición |
|---|---|
| continuidad | La continuidad para un punto existe cuando los límites de los lados izquierdo y derecho coinciden con la función evaluada en ese punto. Para que una función sea continua, la función debe ser continua en cada punto de un dominio ininterrumpido. |
| Continuo | La continuidad para un punto existe cuando los límites de los lados izquierdo y derecho coinciden con la función evaluada en ese punto. Para que una función sea continua, la función debe ser continua en cada punto de un dominio ininterrumpido. |
| Discontinuidades de salto | Las funciones inversas son funciones que se 'deshacen' entre sí. Formalmente\(\ f(x)\) y\(\ g(x)\) son funciones inversas si\(\ f(g(x))=g(f(x))=x\). |
| límite | Un límite es el valor que la salida de una función se acerca a medida que la entrada de la función se acerca a un valor dado. |
| Discontinuidades removibles | Las discontinuidades removibles también se conocen como agujeros. Ocurren cuando los factores pueden ser cancelados algebraicamente a partir de funciones racionales. |
| Discontinuidad removible | Las discontinuidades removibles también se conocen como agujeros. Ocurren cuando los factores pueden ser cancelados algebraicamente a partir de funciones racionales. |
| límite de dos caras | Un límite de dos lados es el valor que una función se acerca tanto desde el lado izquierdo como desde el lado derecho. |
Atribuciones de imagen
- [Figura 1]
Crédito: Fundación CK-12
Licencia: CC BY-SA

