8.1.3: Límites Infinitos

Última actualización
Guardar como PDF

Page ID: 108700

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Límites Infinitos

Geeks-R-Us vende lápices mecánicos de titanio a diseñadores de algoritmos informáticos. En un esfuerzo por atraer más negocios, deciden ejecutar una promoción bastante inusual:

“VENTA!! ¡Cuanto más compres, más ahorras! ¡Los lápices son ahora$\ \$ \frac{12 x}{x-3}$ por docena!”

Si el trillonario, Spug Dense, entra y dice que quiere comprar tantos lápices como Geeks-R-Us pueda resultar, ¿cuál será el costo de los lápices se acercará a medida que el pedido se haga cada vez más grande?

Límites Infinitos

A veces, una función puede no definirse en un número determinado, pero a medida que los valores se ingresan cada vez más cerca del número indefinido, es posible que no exista un límite en la salida. Por ejemplo, para la función f (x) = 1/x (mostrada en las figuras a continuación), a medida que los valores x se toman cada vez más cerca de 0 desde la derecha, la función aumenta indefinidamente. Además, a medida que los valores x se acercan cada vez más a 0 desde la izquierda, la función disminuye indefinidamente.

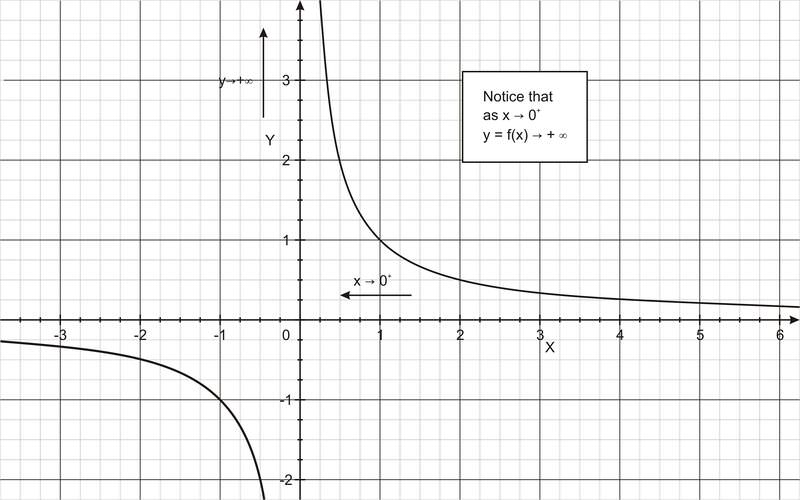
F-d_a1c872907db931401e43c359d41397d7f69e00b102ea5b86fd75d5f5+image_tiny+image_tiny.jpg

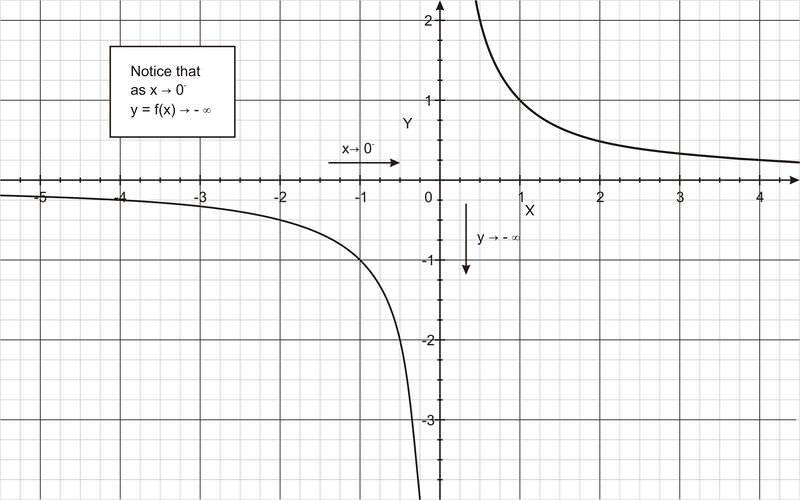
F-d_c3826dde494658e63429a0b807381d0fdd1eea097d6a266123417fec+image_tiny+image_tiny.jpg

Describimos estos comportamientos limitantes escribiendo

\ (\\ comenzar {matriz} {l}
\ lim _ {x\ fila derecha 0^ {+}}\ frac {1} {x} =+\ infty\
\ lim _ {x\ fila derecha 0^ {-}}\ frac {1} {x} =-\ infty
\ end {array}\)

A veces queremos conocer el comportamiento de a$\ f(x)$ medida que x aumenta o disminuye sin ataduras. En este caso nos interesa el comportamiento final de la función, un concepto que probablemente hayas explorado antes. Por ejemplo, ¿cuál es el valor de$\ f(x)=1 / x$ como$\ x$ aumenta o disminuye sin límite? Es decir,

\ (\\ begin {array} {l}
\ lim _ {x\ fila derecha+\ infty}\ frac {1} {x} =? \
\ lim _ {x\ fila derecha-\ infty}\ frac {1} {x} =?
\ end {array}\)

Como puede ver en las gráficas (que se muestran a continuación), como$\ x$ disminuye sin límite, los valores de$\ f(x) = 1/x$ son negativos y se acercan cada vez más a 0. Por otro lado, a medida que$\ x$ aumenta sin límite, los valores de$\ f(x) = 1/x$ son positivos y aún se acercan cada vez más a 0.

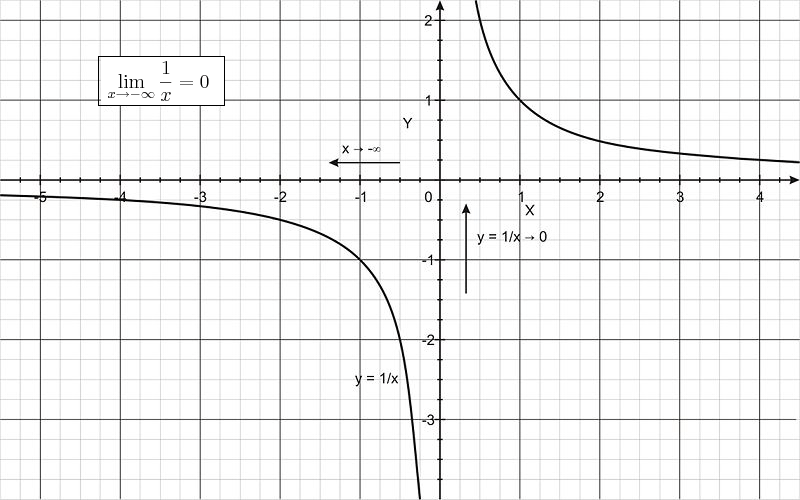
F-D_7309088A49A9161FC50AFC8D722ECEBF0C9766B35ECD49C5F8B9DC00+Image_Tiny+Image_Tiny.png

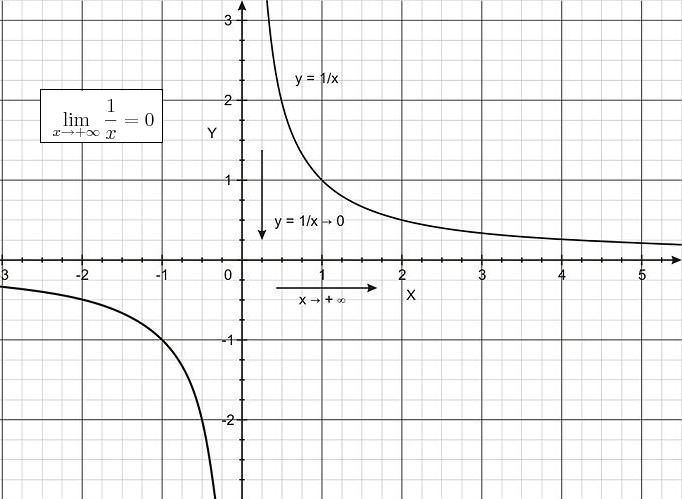
f-d_0084d4e7b6fb07a636d0387fd7cd595878852eda612a5bf27d372d25+image_tiny+image_tiny.png

Es decir,

\ (\\ begin {array} {l}
\ lim _ {x\ fila derecha+\ infty}\ frac {1} {x} =0\\
\ lim _ {x\ fila derecha+\ infty}\ frac {1} {x} =0
\ end {array}\)

Ejemplos

Ejemplo 1

Anteriormente, se le hizo una pregunta sobre la compra de muchos lápices.

Solución

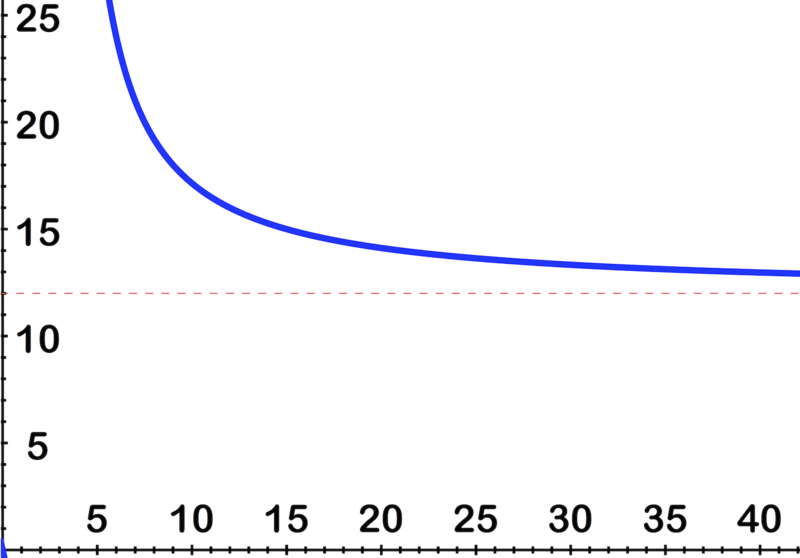
A medida que Spug compra cada vez más lápices, el costo de cada docena bajará rápidamente al principio, y se nivelará después de un tiempo, acercándose a los 12 dólares por docena.

Puedes ver el efecto en la gráfica aquí:

f-d_0e5c44b73a4afe1d566afa190c43d4b4ccb80181b06436a838607e1a+image_tiny+image_tiny.png

Ejemplo 2

Evalúa el límite haciendo una gráfica:$\ \lim _{x \rightarrow 3^{+}} \frac{x+6}{x-3}$

Solución

Al mirar la gráfica:

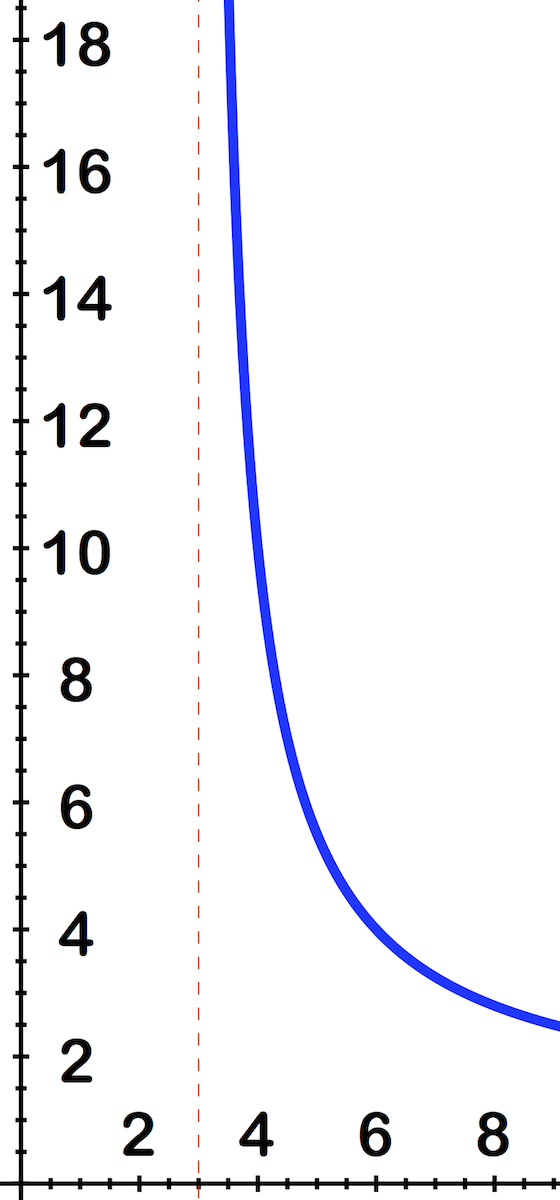
f-d_2ed9cc3b6c1496d1c454ee027600d2bcffc6289da4f8eb10b963f617+image_tiny+image_tiny.png

Podemos ver que a medida que x se acerca cada vez más a 3 desde el lado positivo, la salida aumenta justo fuera de la parte superior de la imagen, en su camino a ∞

Ejemplo 3

Evaluar el límite:$\ \lim _{x \rightarrow \infty} \frac{11 x^{3}-14 x^{2}+8 x+16}{9 x-3}$.

Solución

Para evaluar los límites de las funciones polinómicas, ayuda un poco de intuición. Pensemos esto a través de.

Primero, tenga en cuenta que ya que estamos viendo lo que sucede como la$\ x \rightarrow \infty$ mayoría de las cosas interesantes van a pasar ya que$\ x$ se pone realmente grande.

En la parte superior de la fracción, como x se vuelve realmente masiva, la$\ 11 x^{3}$ parte se hará más grande mucho más rápido que cualquiera de los otros términos. De hecho, aumenta mucho más rápido que los otros términos dejan de importar por completo una vez que x se vuelve realmente monstruoso. Eso significa que la parte importante de la parte superior de la fracción es solo la$\ 11 x^{3}$.

En la parte inferior, se desarrolla una situación similar. Como x se pone muy, muy grande, el -3 importa cada vez menos. Entonces el fondo bien puede ser justo$\ 9x$.

Eso nos da$\ \frac{11 x^{3}}{9 x}$ lo que reduce a$\ \frac{11 x^{2}}{9}$

Ahora podemos ver más fácilmente lo que sucede en los “extremos”. A medida que x se hace cada vez más grande, el numerador sigue creciendo más rápido que el denominador, por lo que la salida general también aumenta.

$\ \therefore \lim _{x \rightarrow+\infty} \frac{11 x^{3}-14 x^{2}+8 x+16}{9 x-3} \text { is }+\infty$

Ejemplo 4

Evaluar$\ \lim _{x \rightarrow 0} \frac{x+2}{x+3}$

Solución

¡Este es más fácil de lo que parece! Como x—>0, dejando solo la fracción: 2/3

Ejemplo 5

Hacer una gráfica para evaluar el límite$\ \lim _{x \rightarrow \infty} \frac{1}{\sqrt{x}}$ y$\ \lim _{x \rightarrow 0^{+}} \frac{1}{\sqrt{x}}$.

Solución

Al mirar la imagen, vemos que a medida que x se vuelve enorme, también lo hace lo$\ \sqrt{x}$ que significa que 1 está siendo dividido por un número cada vez mayor, y el resultado es cada vez más pequeño.

$\ \lim _{x \rightarrow \infty} \frac{1}{\sqrt{x}}=0$

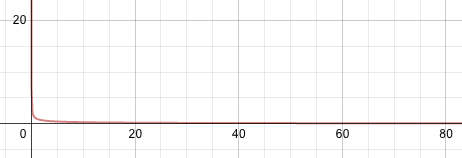
f-d_ecdaafc4cb447edc924f6b1316561ba52409c2e0a1d3429d419bdfea+image_tiny+image_tiny.png

En la misma imagen, podemos ver que a medida que$\ x$ se acerca cada vez más a cero, también lo hace lo$\ \sqrt{x}$ que significa que 1 se está dividiendo por un número cada vez menor, y el resultado se hace cada vez más grande.

$\ \lim _{x \rightarrow 0^{+}} \frac{1}{\sqrt{x}} \text { is }+\infty$

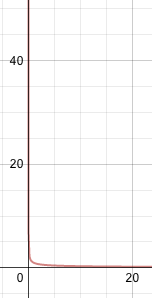
f-d_e07efe198e9ee2b280196f3f92ac48bf8853a5c4d99e633b85503ec5+image_tiny+image_tiny.png

Ejemplo 6

Graficar y evaluar el límite:$\ \lim _{x \rightarrow 2^{+}} \frac{1}{x-2}$.

Solución

Al mirar la imagen, podemos ver que a medida que x se acerca cada vez más a 2 desde la dirección positiva, 1 se divide por números cada vez más pequeños, por lo que el resultado se hace cada vez más grande.

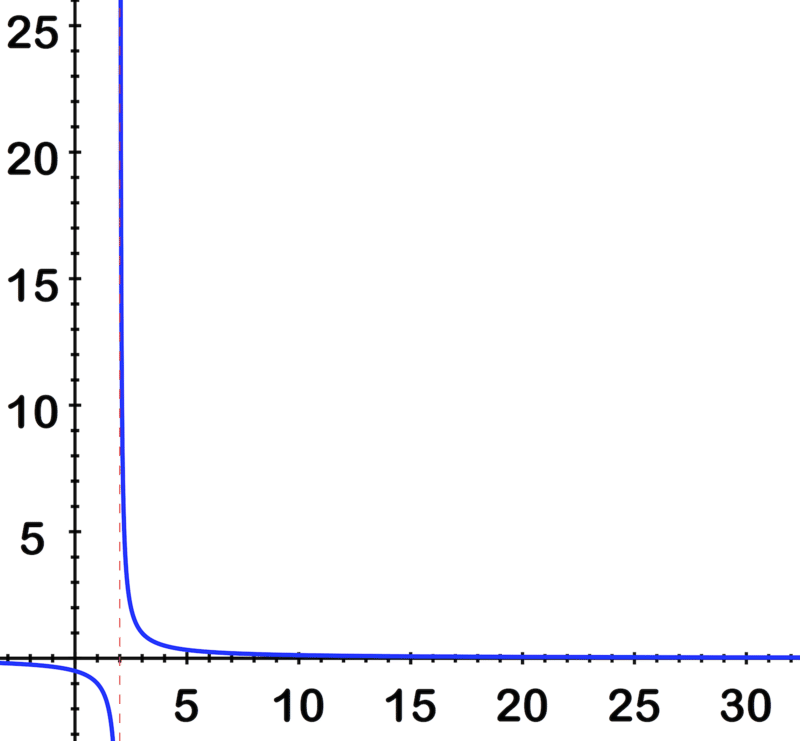
f-d_8cf47c13f17f1acb89275c566befe39ffb76766bcaacc6e46d196ece+image_tiny+image_tiny.png

$\ \lim _{x \rightarrow 2^{+}} \frac{1}{x-2} \text { is }+\infty$

Revisar

Evaluar los límites:

$\ \lim _{x \rightarrow 3^{-}} \frac{1}{x-3}$
$\ \lim _{x \rightarrow-4^{+}} \frac{1}{x+4}$
$\ \lim _{x \rightarrow-\left(\frac{8}{3}\right)^{+}} \frac{1}{3 x+8}$
$\ \lim _{x \rightarrow-5^{+}} \frac{\left(x^{2}+11 x+30\right)}{x+5}$
$\ \lim _{x \rightarrow-\infty} \frac{\left(x^{2}+11 x+30\right)}{x+5}$
$\ \lim _{x \rightarrow \infty} \frac{-11 x^{3}+20 x^{2}+15 x-17}{-9 x^{3}+5 x^{2}-x-17}$
$\ \lim _{x \rightarrow \infty} 13$
$\ \lim _{x \rightarrow \infty} \frac{-2 x+18}{17 x-3}$
$\ \lim _{x \rightarrow \infty} 15$
$\ \lim _{x \rightarrow \infty}-5 x^{2}+5 x+14$
$\ \lim _{x \rightarrow \infty} 7 x+12$
$\ \lim _{x \rightarrow \infty}-3 x+13$
$\ \lim _{x \rightarrow \infty} \frac{13 x-8}{19 x^{3}-11 x^{2}+x+4}$
$\ \lim _{x \rightarrow \infty}-17 x+14$
$\ \lim _{x \rightarrow \infty}-7 x^{2}-2 x-13$

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.3.

El vocabulario

Término	Definición
límite	Un límite es el valor que la salida de una función se acerca a medida que la entrada de la función se acerca a un valor dado.

Search

Text Color

Text Size

Margin Size

Font Type

Ejemplo 1

Ejemplo 2

Ejemplo 3

Ejemplo 4

Ejemplo 5

Ejemplo 6