3.12: Cuadrados Punnett
- Page ID
- 108197
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
¿Qué obtienes cuando cruzas una manzana y una naranja?
Aunque el fruto anterior puede no resultar, sería bueno predecir científicamente lo que resultaría. La predicción de los posibles genotipos y fenotipos a partir de un cruce genético suele ser ayudada por un cuadrado de Punnett.
Cuadrados Punnett
Un cuadrado de Punnett es un gráfico que permite determinar fácilmente el porcentaje esperado de diferentes genotipos en la descendencia de dos padres. Un ejemplo de un cuadrado Punnett para plantas de guisante se muestra en la siguiente figura. En este ejemplo, ambos progenitores son heterocigotos para el color de la flor (Bb). Los gametos producidos por el padre masculino están en la parte superior de la tabla, y los gametos producidos por el progenitor femenino están a lo largo del costado. Las diferentes combinaciones posibles de alelos en su descendencia se determinan rellenando las celdas del cuadrado Punnett con las letras correctas (alelos).
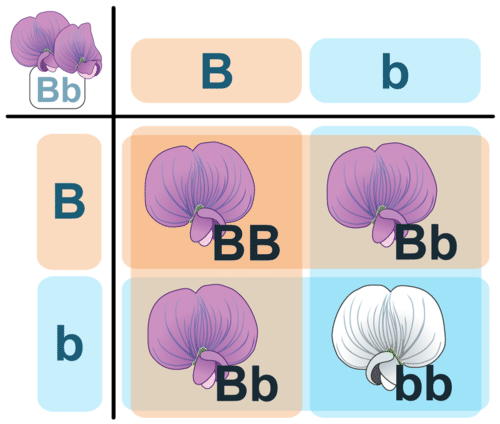Este cuadrado de Punnett muestra un cruce entre dos heterocigotos, Bb. ¿Sabes de dónde viene cada letra (alelo) en las cuatro celdas? Se cruzan dos plantas de guisante, ambas heterocigóticas para el color de la flor. La descendencia mostrará la coloración púrpura dominante en una proporción 3:1. O, alrededor del 75% de la descendencia será de color púrpura. Predicción de genotipos de descendencia
En el cruce mostrado en la Figura anterior, se puede observar que una de cada cuatro crías (25 por ciento) tiene el genotipo BB, una de cada cuatro (25 por ciento) tiene el genotipo bb, y dos de cada cuatro (50 por ciento) tienen el genotipo Bb. Estos porcentajes de genotipos son lo que esperarías en cualquier cruce entre dos progenitores heterocigóticos. Por supuesto, cuando solo se producen cuatro crías, los porcentajes reales de genotipos pueden variar por casualidad de los porcentajes esperados. No obstante, si consideraras cientos de cruces de este tipo y miles de crías, te acercarías mucho a los resultados esperados, al igual que lanzar una moneda.
Predicción de fenotipos de descendencia
Se pueden predecir los porcentajes de fenotipos en la descendencia de este cruce a partir de sus genotipos. B es dominante a b, por lo que las crías con el genotipo BB o Bb tendrán el fenotipo de flor morada. Solo las crías con el genotipo bb tendrán el fenotipo de flor blanca. Por lo tanto, en este cruce, se esperaría que tres de cada cuatro (75 por ciento) de las crías tuvieran flores moradas y una de cada cuatro (25 por ciento) tuviera flores blancas. Estos son los mismos porcentajes que obtuvo Mendel en su primer experimento.
Determinación de genotipos faltantes
También se puede utilizar un cuadrado Punnett para determinar un genotipo faltante basado en los otros genotipos involucrados en un cruce. Supongamos que tienes una planta madre con flores moradas y una planta madre con flores blancas. Debido a que el alelo b es recesivo, sabes que el progenitor de flores blancas debe tener el genotipo bb. El progenitor de flores púrpuras, por otro lado, podría tener el genotipo BB o el genotipo Bb. El cuadrado de Punnett en la Figura de abajo muestra esta cruz. Los signos de interrogación (?) en el gráfico podrían ser alelos B o b.
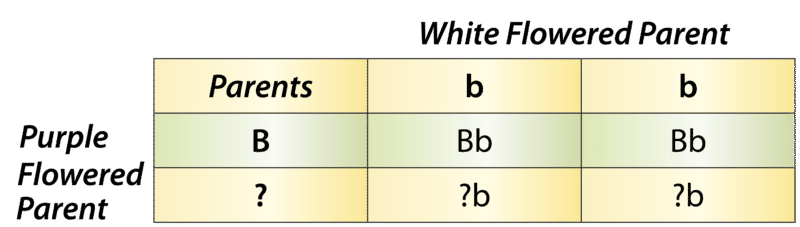Punnett Square: Cruce Entre Plantas De Guisantes De Flores Blancas y Moradas. Este cuadrado de Punnett muestra un cruce entre una planta de guisante de flores blancas y una planta de guisante de flores moradas. ¿Se pueden rellenar los alelos faltantes? ¿Qué necesitas saber sobre la descendencia para completar sus genotipos? ¿Se puede decir cuál es el genotipo del padre de flores moradas a partir de la información en la plaza Punnett? No; también es necesario conocer los genotipos de la descendencia en la fila 2. ¿Y si descubres que dos de las cuatro crías tienen flores blancas? Ahora ya sabes que la descendencia en la segunda fila debe tener el genotipo bb. Uno de sus alelos b obviamente proviene del padre de flores blancas (bb), porque ese es el único alelo que tiene este padre. El otro alelo b debe provenir del progenitor de flores púrpuras. Por lo tanto, el progenitor con flores moradas debe tener el genotipo Bb.
Punnett Square para dos características
Cuando consideras más de una característica a la vez, usar un cuadrado Punnett es más complicado. Esto se debe a que son posibles muchas más combinaciones de alelos. Por ejemplo, con dos genes cada uno teniendo dos alelos, un individuo tiene cuatro alelos, y estos cuatro alelos pueden ocurrir en 16 combinaciones diferentes. Esto se ilustra para las plantas de guisante en la Figura siguiente. En este cruce, conocido como cruce dihíbrido, ambos progenitores son heterocigotos para el color de vaina (Gg) y la forma de vaina (Ff).
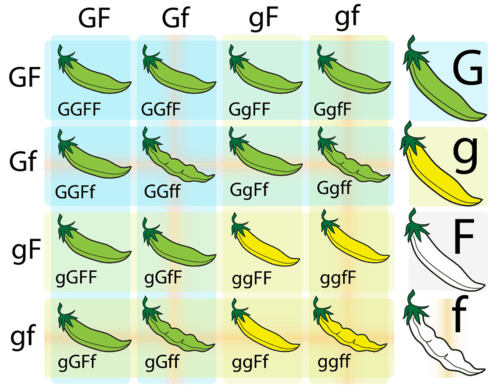Punnett Cuadrado para Dos Características. Este cuadrado de Punnett representa un cruce entre dos plantas de guisante que son heterocigóticas para dos características. G representa el alelo dominante para el color de vaina verde y g representa el alelo recesivo para el color amarillo de la vaina. F representa el alelo dominante para la forma de vaina completa, y f representa el alelo recesivo para la forma de vaina constreñida. Resumen
- Un cuadrado de Punnett es una gráfica que permite determinar los porcentajes esperados de diferentes genotipos en la descendencia de dos padres.
- Un cuadrado de Punnett permite la predicción de los porcentajes de fenotipos en la descendencia de un cruce de genotipos conocidos.
- Un cuadrado Punnett puede ser utilizado para determinar un genotipo faltante basado en los otros genotipos involucrados en un cruce.
Revisar
- ¿Qué es un cuadrado Punnett? ¿Cómo se usa?
- Dibuja un cuadrado Punnett de una cruz de Ss x ss. El alelo S codifica tallos largos en plantas de guisante y el alelo s codifica para tallos cortos. Si S es dominante a s, ¿qué porcentaje de la descendencia esperarías tener cada fenotipo?
- ¿Qué letra debe sustituir a los signos de interrogación (?) en esta plaza Punnett? Explique cómo sabe.
-
¿En qué se diferencian los cuadrados de Punnett para un cruce monohíbrido y un cruce dihíbrido?
- ¿Cuáles son los genotipos de gametos de una autopolinización de AAbB?
-
Mendel realizó un cruce dihíbrido para examinar la herencia de las características para el color y la forma de la semilla. El alelo dominante para el color amarillo de la semilla es Y, y el alelo recesivo para el color verde es y. El alelo dominante para semillas redondas es R, y el alelo recesivo para una forma arrugada es r. Las dos plantas que se cruzaron fueron los dihíbridos F1 RRyy. Identificar las proporciones de rasgos que Mendel observó en la generación F2. Crea un cuadrado Punnett para ayudarte a responder la pregunta.
| Imagen | Referencia | Atribuciones |
|
[Figura 1] | Crédito: Mariana Ruiz Villarreal (LadyOfHats) para Fundación CK-12 Fuente: Fundación CK-12 Licencia: CC BY-NC |
 |
[Figura 2] | Crédito: Mariana Ruiz Villarreal (LadyOfHats) para Fundación CK-12; Sam McCabe; Jodi So Fuente: Fundación CK-12 Licencia: CC BY-NC 3.0 |
|
[Figura 3] | Crédito: Jodi So; Sam McCabe Fuente: Fundación CK-12 Licencia: CC BY-NC 3.0 |
 |
[Figura 4] | Crédito: Mariana Ruiz Villarreal (LadyOfHats) para Fundación CK-12; Sam McCabe; Jodi So Fuente: Fundación CK-12 Licencia: CC BY-NC 3.0 |
|
[Figura 5] | Crédito: Mariana Ruiz Villarreal (LadyOfHats) para Fundación CK-12 Fuente: Fundación CK-12 Licencia: CC BY-NC |