3.11: Probabilidad
- Page ID
- 108164
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
¿Cuáles son las probabilidades de volver a aterrizar en 25?
No tan alto como heredar un alelo de un padre. La probabilidad juega un papel importante en la determinación de la posibilidad de heredar un alelo de un padre. Es similar a lanzar una moneda. ¿Cuál es la probabilidad de que la moneda aterrice en las cabezas?
Probabilidad
Supongamos que eres un obtentor de plantas tratando de desarrollar una nueva variedad de plantas que sea más útil para los humanos. Planeas polinizar de forma cruzada una planta resistente a insectos con una planta que crece rápidamente. Tu objetivo es producir una variedad de plantas que sean resistentes a los insectos y de rápido crecimiento. ¿Qué porcentaje de la descendencia esperarías que tuviera ambas características? Las leyes de Mendel pueden ser utilizadas para averiguarlo. No obstante, para entender cómo se pueden utilizar de esta manera las leyes de Mendel, primero hay que conocer la probabilidad.
La probabilidad es la probabilidad, o probabilidad, de que ocurra un determinado evento. La forma más fácil de entender la probabilidad es con los tirados de monedas (ver la Figura a continuación). Cuando arrojas una moneda, la probabilidad de que una cabeza gire hacia arriba es del 50 por ciento. Esto se debe a que una moneda solo tiene dos caras, por lo que existe la misma posibilidad de que una cabeza o una cola se vuelquen en cualquier lanzamiento dado.
Lanzar una Moneda. Las competencias a menudo comienzan con el tirar una moneda. ¿Por qué es esta una manera justa de decidir quién va primero? Si eliges cabezas, ¿cuál es la posibilidad de que el tiro salga a tu manera? Si arrojas una moneda dos veces, podrías esperar obtener una cabeza y una cola. Pero cada vez que arrojas la moneda, la probabilidad de una cabeza sigue siendo del 50 por ciento. Por lo tanto, es muy probable que consigas dos o incluso varias cabezas (o colas) seguidas. ¿Y si tiraste una moneda diez veces? Probablemente obtendrías más o menos de las cinco cabezas esperadas. Por ejemplo, podrías obtener siete cabezas (70 por ciento) y tres colas (30 por ciento). Cuantas más veces arrojes la moneda, sin embargo, más te acercarás al 50 por ciento de cabezas. Por ejemplo, si tiraste una moneda 1000 veces, podrías obtener 510 cabezas y 490 colas.
Probabilidad y Herencia
Las mismas reglas de probabilidad en el lanzamiento de monedas se aplican a los principales eventos que determinan los genotipos de descendencia. Estos eventos son la formación de gametos durante la meiosis y la unión de gametos durante la fertilización.
Probabilidad y formación de gametos
¿Cómo es la formación de gametos como lanzar una moneda? Considera nuevamente las plantas de guisantes de flores moradas de Mendel. Supongamos que una planta es heterocigota para el alelo de color flor, por lo que tiene el genotipo Bb (ver la Figura a continuación). Durante la meiosis, los cromosomas homólogos, y los alelos que portan, se segregan y van a diferentes gametos. Por lo tanto, cuando la planta de guisante Bb forma gametos, los alelos B y b se segregan y van a diferentes gametos. En consecuencia, la mitad de los gametos producidos por el padre Bb tendrán el alelo B y la mitad tendrá el alelo b. Con base en las reglas de probabilidad, cualquier gameto dado de este padre tiene un 50 por ciento de probabilidad de tener el alelo B y un 50 por ciento de probabilidad de tener el alelo b.
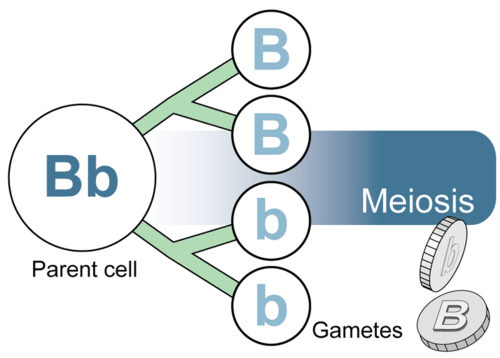Formación de gametos por meiosis. Los alelos emparejados siempre se separan y van a diferentes gametos durante la meiosis. Probabilidad y Fertilización
¿Cuál de estos gametos se une en la fertilización con el gameto de otra planta madre? Esto es una cuestión de azar, como lanzar una moneda. Así, podemos suponer que cualquier tipo de juego —uno con el alelo B o uno con el alelo b — tiene las mismas posibilidades de unirse con cualquiera de los gametos producidos por el otro progenitor. Ahora supongamos que el otro padre también es Bb. Si los gametos de dos padres Bb se unen, ¿cuál es la probabilidad de que la descendencia tenga uno de cada alelo como los padres (Bb)? ¿Cuál es la probabilidad de que tengan una combinación de alelos diferente a la de los padres (ya sea BB o bb)? Para responder a estas preguntas, los genetistas utilizan una herramienta sencilla llamada Cuadrado Punnett, que es el foco del siguiente concepto.
Resumen
- La probabilidad es la posibilidad de que ocurra un determinado evento. Por ejemplo, la probabilidad de que una cabeza gire hacia arriba en cualquier tirada de moneda dada es del 50 por ciento.
- La probabilidad se puede utilizar para predecir la probabilidad de que los gametos y la descendencia tengan ciertos alelos.
Revisar
- Definir probabilidad. Aplicar el término a un tiro de moneda.
- ¿Cómo es la formación de gametos como lanzar una moneda?
- Con un homocigoto BB, ¿cuál es la probabilidad de que un gameto tenga el alelo B? ¿El alelo b?
| Imagen | Referencia | Atribuciones |
|
[Figura 1] | Crédito: Mariana Ruiz Villarreal (LadyOfHats) para Fundación CK-12 Fuente: Fundación CK-12 Licencia: CC BY-NC 3.0 |
 |
[Figura 2] | Crédito: Image copyright Anneka, 2014 Fuente: http://www.shutterstock.com Licencia: Usado bajo licencia de Shutterstock.com |
 |
[Figura 3] | Crédito: Mariana Ruiz Villarreal (LadyOfHats) para Fundación CK-12 Fuente: Fundación CK-12 Licencia: CC BY-NC 3.0 |