1.1: Concepto de Límite
- Page ID
- 105966
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al aprender sobre el comportamiento final de una función racional, la describías como que tiene una asíntota horizontal en cero u otro número, o yendo al infinito. La notación límite es una forma de describir matemáticamente este comportamiento final.
Ya sabes que a medida que x se vuelve extremadamente grande entonces la función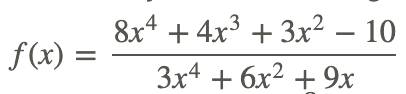
va 8/3 porque la mayor potencia son iguales y 8/3 es la ración de los coeficientes principales. ¿Cómo se representa esta declaración usando notación límite?
Introducción a los límites
La notación límite es una forma de afirmar una idea que es un poco más sutil que simplemente decir x=5 o y=3.
La letra a puede ser cualquier número o infinito. La función f (x) es cualquier función de x. La letra b puede ser cualquier número. Si la función va al infinito, entonces en lugar de escribir “=∞” deberías escribir que el límite no existe o “DNE”. Esto se debe a que el infinito no es un número. Si una función va al infinito entonces no tiene límite.
Tome el siguiente límite:
El límite de y=4x 2 a medida que x se acerca a 2 es 16
En notación límite, esto sería:
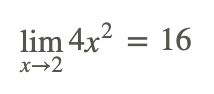
Si bien es posible que una función nunca alcance realmente una altura de b, se acercará arbitrariamente a b. Una forma de pensar sobre el concepto de límite es usar un ejemplo físico. Párese a cierta distancia de una pared y luego dé un gran paso para llegar a la mitad de la pared. Da otro paso para volver a ir a mitad de camino a la pared. Si sigues dando pasos que te llevan a mitad de camino a la pared entonces van a pasar dos cosas. Primero, te acercarás extremadamente a la pared pero nunca llegarás a la pared independientemente de cuántos pasos des. Segundo, un observador que desee describir su situación notaría que el muro actúa como un límite a lo lejos que puede llegar.
Ejemplos
Ejemplo 1
Anteriormente, se le preguntó cómo escribir la declaración “El límite de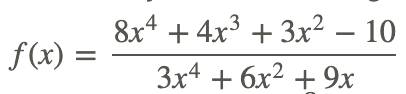
a medida que x se acerca al infinito es 8/3 "en notación límite.
Esto se puede escribir usando notación límite como:
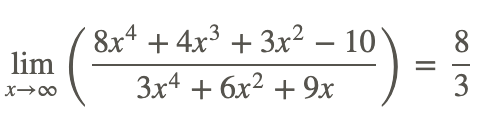
Ejemplo 2
Traducir la siguiente declaración matemática en palabras.
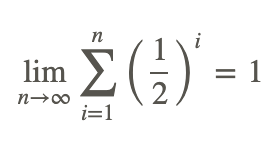
El límite de la suma de 1/2 + 1/4 + 1/8 +a medida que el número de términos se acerca al infinito es 1.
Ejemplo 3
Utilice la notación de límite para representar la siguiente declaración matemática.
1/3 + 1/9 + 1/27 += 1/2
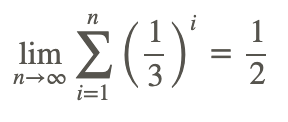
Ejemplo 4
Describir el comportamiento final de la siguiente función racional al infinito y al infinito negativo usando límites.
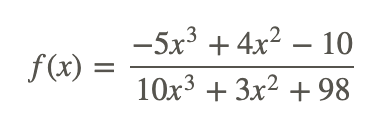
Dado que la función tiene potencias iguales de x en el numerador y en el denominador, el comportamiento final es − 1/2 ya que x va al infinito tanto positivo como negativo.
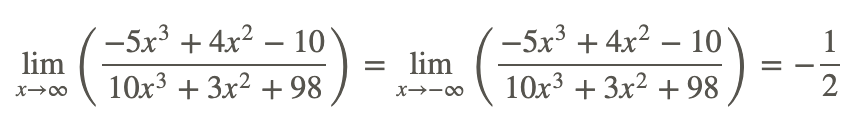
Ejemplo 5
Traduzca la siguiente expresión limit en palabras. ¿Qué notas sobre la expresión límite?
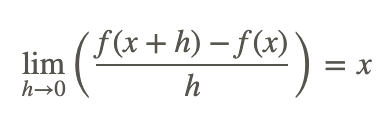
El límite de la relación de la diferencia entre f de cantidad x más h y f de x y h a medida que h se acerca a 0 es x.
Deberías notar que h→0 no significa h=0 porque si lo hiciera entonces no podrías tener un 0 en el denominador. También debes tener en cuenta que en el numerador, f (x+h) y f (x) van a estar súper cerca entre sí a medida que h se acerca a cero. El cálculo te permitirá lidiar con problemas que parecen parecerse a 0/0 y ∞/∞.
Revisar
Describir el comportamiento final de las siguientes funciones racionales al infinito y al infinito negativo usando límites.
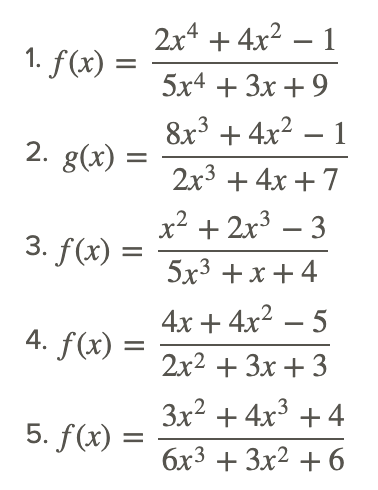
Traducir las siguientes declaraciones en notación límite.
6. El límite de y=2x 2 +1 a medida que x se acerca a 3 es 19.
7. El límite de y=e x a medida que x se acerca al infinito negativo es 0.
8. El límite de y= 1/x a medida que x se acerca al infinito es 0.
Utilice la notación de límite para representar las siguientes declaraciones matemáticas.
9. 1/4 + 1/16 + 1/64 += 1/3
10. La serie 1+ 1/2 + 1/3 + 1/4 +diverge.
11. 1+ 1/2 + 1/4 + 1/8 +=2
12. 9/10 + 9/100 + 9/1000 +=1
Traducir las siguientes declaraciones matemáticas en palabras.
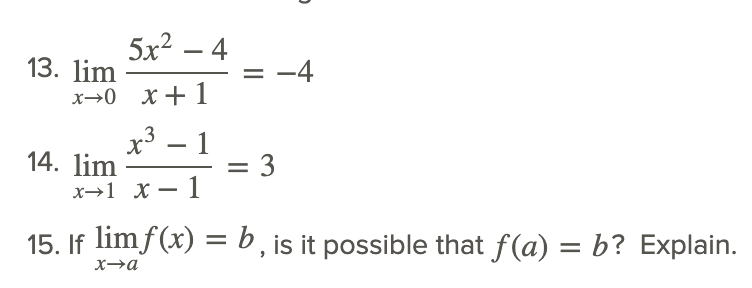
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 14.1.
El vocabulario
| Término | Definición |
|---|---|
| Comportamiento final | El comportamiento final es una descripción de la tendencia de una función ya que los valores de entrada se vuelven muy grandes o muy pequeños, representados como los 'extremos' de una función gráfica. |
| Asintota horizontal | Una asíntota horizontal es una línea horizontal que indica dónde se aplana una función ya que la variable independiente se vuelve muy grande o muy pequeña. Una función puede tocar o pasar a través de una asíntota horizontal. |
| notación límite | La notación límite es una forma de expresar el hecho de que una función se acerca arbitrariamente a un valor. |
Recurso Adicional
PLIX: Juega, aprende, interactúa, explora - Concepto de límite
Video: Introducción a los límites
Práctica: Concepto de límite
Mundo real: Suiting Up