4.6: Límites al infinito y asíntotas

Última actualización
Guardar como PDF

Page ID: 116505

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Calcular el límite de una función a medida que$x$ aumenta o disminuye sin límite.
Reconocer una asíntota horizontal en la gráfica de una función.
Estimar el comportamiento final de una función a medida que$x$ aumenta o disminuye sin límite.
Reconocer una asíntota oblicua en la gráfica de una función.
Analizar una función y sus derivadas para dibujar su gráfica.

Hemos mostrado cómo usar la primera y segunda derivada de una función para describir la forma de una gráfica. Para graficar una función$f$ definida en un dominio ilimitado, también necesitamos conocer el comportamiento de$f$ as$x→±∞$. En esta sección, definimos límites al infinito y mostramos cómo estos límites afectan la gráfica de una función. Al final de esta sección, esbozamos una estrategia para graficar una función arbitraria$f$.

Comenzamos examinando lo que significa para una función tener un límite finito en el infinito. Luego estudiamos la idea de una función con un límite infinito en el infinito. De vuelta en Introducción a Funciones y Gráficas, observamos asíntotas verticales; en esta sección tratamos asíntotas horizontales y oblicuas.

Límites en el infinito y asíntotas horizontales

Recordemos que$\displaystyle \lim_{x→a}f(x)=L$ los medios$f(x)$ se vuelven arbitrariamente cercanos a$L$ siempre y cuando$x$ esté suficientemente cerca de$a$. Podemos extender esta idea a límites al infinito. Por ejemplo, considere la función$f(x)=2+\frac{1}{x}$. Como se puede observar gráficamente en la Figura$\PageIndex{1}$ y numéricamente en la Tabla$\PageIndex{1}$, a medida que los valores de se$x$ hacen mayores, los valores de$f(x)$ aproximación$2$. Decimos el límite como$x$ aproximaciones$∞$ de$f(x)$ es$2$ y escribimos$\displaystyle \lim_{x→∞}f(x)=2$. De igual manera, para$x<0$, a medida que los valores se$|x|$ hacen mayores, los valores de$f(x)$ aproximación$2$. Decimos el límite como$x$ aproximaciones$−∞$ de$f(x)$ es$2$ y escribimos$\displaystyle \lim_{x→−∞}f(x)=2$.

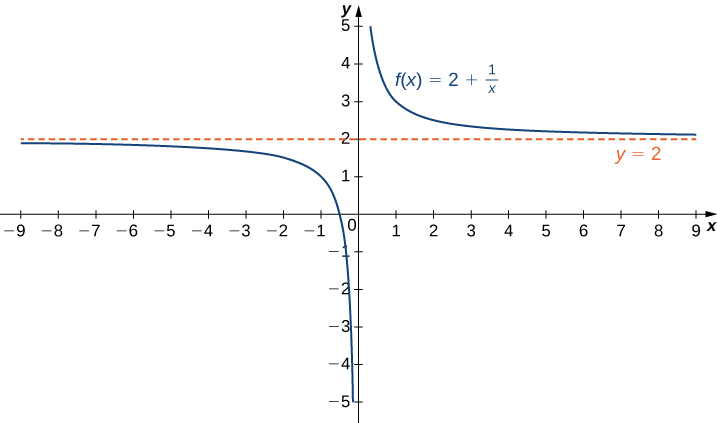
Se grafica la función f (x) 2 + 1/x. La función comienza negativa cerca de y = 2 pero luego disminuye a −∞ cerca de x = 0. La función luego disminuye desde ∞ cerca de x = 0 y se acerca a y = 2 a medida que x aumenta. Hay una línea horizontal que denota la asíntota y = 2. — Figura: La$\PageIndex{1}$ función se acerca a la asíntota a medida que se$y=2$ aproxima$x$.$±∞$

Tabla$\PageIndex{1}$: Valores de una función$f$ como$x→±∞$
$x$	10	100	1,000	10,000
$2+\frac{1}{x}$	2.1	2.01	2.001	2.0001
$x$	−10	−100	−1000	−10,000
$2+\frac{1}{x}$	1.9	1.99	1.999	1.9999

De manera más general, para cualquier función$f$, decimos que el límite a partir$x→∞$ de$f(x)$ es$L$ si$f(x)$ se vuelve arbitrariamente cercano a$L$ siempre y cuando$x$ sea suficientemente grande. En ese caso, escribimos$\displaystyle \lim_{x→∞}f(x)=L$. De igual manera, decimos que el límite a partir$x→−∞$ de$f(x)$ es$L$ si$f(x)$ se vuelve arbitrariamente cercano al$L$ tiempo$x<0$ y$|x|$ es suficientemente grande. En ese caso, escribimos$\displaystyle \lim_{x→−∞}f(x)=L$. Ahora nos fijamos en la definición de una función que tiene un límite en el infinito.

Definición: Límite al Infinito (Informal)

Si los valores de$f(x)$ llegar a ser arbitrariamente cercanos a$L$ como$x$ se vuelve suficientemente grande, decimos que la función$f$ tiene un límite en el infinito y escribimos

\[\lim_{x→∞}f(x)=L. \nonumber \]

Si los valores de$f(x)$ se vuelven arbitrariamente cercanos a$L$ for$x<0$ como$|x|$ se vuelve suficientemente grande, decimos que la función$f$ tiene un límite en el infinito negativo y escribimos

\[\lim_{x→−∞}f(x)=L. \nonumber \]

Si los valores$f(x)$ se acercan arbitrariamente a algún valor finito$L$ como$x→∞$ o$x→−∞$, la gráfica de$f$ se acerca a la línea$y=L$. En ese caso, la línea$y=L$ es una asíntota horizontal de$f$ (Figura$\PageIndex{2}$). Por ejemplo, para la función$f(x)=\dfrac{1}{x}$, ya que$\displaystyle \lim_{x→∞}f(x)=0$, la línea$y=0$ es una asíntota horizontal de$f(x)=\dfrac{1}{x}$.

La figura se divide en dos figuras etiquetadas como a y b. La figura a muestra una función f (x) acercándose pero nunca tocando una línea discontinua horizontal etiquetada como L desde arriba. La figura b muestra una función f (x) acercándose pero nunca una línea discontinua horizontal etiquetada M desde abajo. — Figura$\PageIndex{2}$: (a) As$x→∞$, los valores de$f$ se acercan arbitrariamente a$L$. La línea$y=L$ es una asíntota horizontal de$f$. b) Como$x→−∞$, los valores de$f$ se acercan arbitrariamente a$M$. La línea$y=M$ es una asíntota horizontal de$f$.

Definición: Asíntota horizontal

Si$\displaystyle \lim_{x→∞}f(x)=L$ o$\displaystyle \lim_{x→−∞}f(x)=L$, decimos que la línea$y=L$ es una asíntota horizontal de$f$.

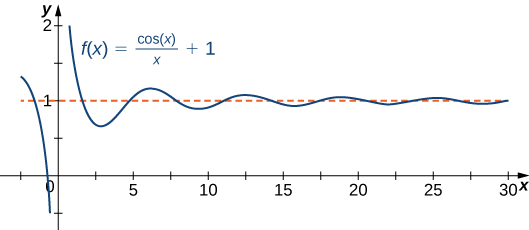
Una función no puede cruzar una asíntota vertical porque la gráfica debe acercarse al infinito (o$ −∞$) desde al menos una dirección cuando se$x$ acerca a la asíntota vertical. Sin embargo, una función puede cruzar una asíntota horizontal. De hecho, una función puede cruzar una asíntota horizontal un número ilimitado de veces. Por ejemplo, la función$f(x)=\dfrac{\cos x}{x}+1$ mostrada en la Figura$\PageIndex{3}$ cruza la asíntota horizontal$y=1$ un número infinito de veces a medida que oscila alrededor de la asíntota con amplitud siempre decreciente.

Se muestra la función f (x) = (cos x) /x + 1. Disminuye de (0, ∞) y luego procede a oscilar alrededor de y = 1 con amplitud decreciente. — Figura$\PageIndex{3}$: La gráfica de$f(x)=(\cos x)/x+1$ cruza su asíntota horizontal$y=1$ un número infinito de veces.

Las leyes algebraicas de límite y el teorema de squeeze que introdujimos en Introducción a los límites también se aplican a los límites al infinito. Ilustramos cómo usar estas leyes para computar varios límites al infinito.

Ejemplo$\PageIndex{1}$: Computing Limits at Infinity

Para cada una de las siguientes funciones$f$, evaluar$\displaystyle \lim_{x→∞}f(x)$ y$\displaystyle \lim_{x→−∞}f(x)$. Determinar las asíntotas horizontales para$f$.

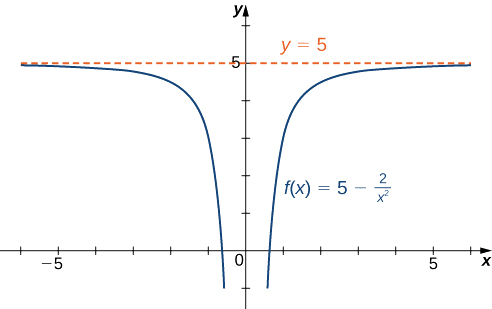
$f(x)=5−\dfrac{2}{x^2}$
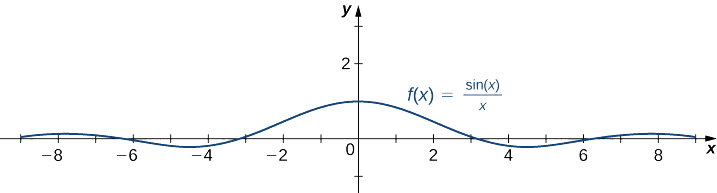
$f(x)=\dfrac{\sin x}{x}$
$f(x)=\tan^{−1}(x)$

Solución

a. Usando las leyes de límite algebraico, tenemos

\[\lim_{x→∞}\left(5−\frac{2}{x^2}\right)=\lim_{x→∞}5−2\left(\lim_{x→∞}\frac{1}{x}\right)\cdot\left(\lim_{x→∞}\frac{1}{x}\right)=5−2⋅0=5.\nonumber \]

De igual manera,$\displaystyle \lim_{x→−∞}f(x)=5$. Por lo tanto,$f(x)=5-\dfrac{2}{x^2}$ tiene una asíntota horizontal$y=5$ y$f$ se acerca a esta asíntota horizontal$x→±∞$ como se muestra en la siguiente gráfica.

Se grafica la función f (x) = 5 — 2/x2. La función se acerca a la asíntota horizontal y = 5 a medida que x se acerca a ±∞. — Figura$\PageIndex{4}$: Esta función se aproxima a una asíntota horizontal como$x→±∞.$

b. ya que$-1≤\sin x≤1$ para todos$x$, tenemos

\[\frac{−1}{x}≤\frac{\sin x}{x}≤\frac{1}{x}\nonumber \]

para todos$x≠0$. También, desde

$\displaystyle \lim_{x→∞}\frac{−1}{x}=0=\lim_{x→∞}\frac{1}{x}$,

podemos aplicar el teorema squeeze para concluir que

$\displaystyle \lim_{x→∞}\frac{\sin x}{x}=0.$

Del mismo modo,

$\displaystyle \lim_{x→−∞}\frac{\sin x}{x}=0.$

Así,$f(x)=\dfrac{\sin x}{x}$ tiene una asíntota horizontal$y=0$ y$f(x)$ se acerca a esta asíntota horizontal$x→±∞$ como se muestra en la siguiente gráfica.

Se muestra la función f (x) = (sin x) /x. Tiene un máximo global en (0, 1) y luego procede a oscilar alrededor de y = 0 con amplitud decreciente. — Figura$\PageIndex{5}$: Esta función cruza su asíntota horizontal varias veces.

c. Evaluar$\displaystyle \lim_{x→∞}\tan^{−1}(x)$ y$\displaystyle \lim_{x→−∞}\tan^{−1}(x)$, primero consideramos la gráfica de$y=\tan(x)$ sobre el intervalo$\left(−\frac{π}{2},\frac{π}{2}\right)$ como se muestra en la siguiente gráfica.

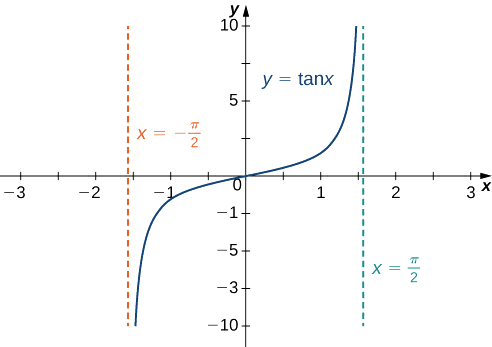
Desde

$\displaystyle \lim_{x→\tfrac{π}{2}^−}\tan x=∞,$

se deduce que

$\displaystyle \lim_{x→∞}\tan^{−1}(x)=\frac{π}{2}.$

Del mismo modo, dado que

$\displaystyle \lim_{x→-\tfrac{π}{2}^+}\tan x=−∞,$

se deduce que

$\displaystyle \lim_{x→−∞}\tan^{−1}(x)=−\frac{π}{2}.$

Como resultado,$y=\frac{π}{2}$ y$y=−\frac{π}{2}$ son asíntotas horizontales de$f(x)=\tan^{−1}(x)$ como se muestra en la siguiente gráfica.

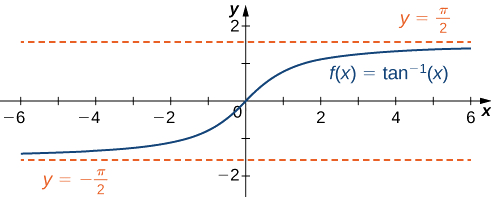
Se muestra la función f (x) = tan−1 x. Aumenta desde (−∞, −π/2), pasa por el origen y luego aumenta hacia (∞, π/2). Hay líneas discontinuas horizontales marcando y = ±π/2. — Figura$\PageIndex{7}$: Esta función tiene dos asíntotas horizontales.

Ejercicio$\PageIndex{1}$

Evaluar$\displaystyle \lim_{x→−∞}\left(3+\frac{4}{x}\right)$ y$\displaystyle \lim_{x→∞}\left(3+\dfrac{4}{x}\right)$. Determinar las asíntotas horizontales de$f(x)=3+\frac{4}{x},$ si las hubiere.

Pista: $\displaystyle \lim_{x→±∞}\frac{1}{x}=0$

Contestar: Ambos límites son$3.$ La línea$y=3$ es una asíntota horizontal.

Límites infinitos en el infinito

A veces los valores de una función$f$ se vuelven arbitrariamente grandes como$x→∞ $ (o como$x→−∞$). En este caso, escribimos$\displaystyle \lim_{x→∞}f(x)=∞$ (o$\displaystyle \lim_{x→−∞}f(x)=∞$). Por otro lado, si los valores de$f$ son negativos pero llegan a ser arbitrariamente grandes en magnitud como$x→∞$ (o como$x→−∞$), escribimos$\displaystyle \lim_{x→∞}f(x)=−∞$ (o$\displaystyle \lim_{x→−∞}f(x)=−∞$).

Por ejemplo, considere la función$f(x)=x^3$. Como se ve en Tabla$\PageIndex{2}$ y Figura$\PageIndex{8}$, a medida$x→∞$ que los valores$f(x)$ se vuelven arbitrariamente grandes. Por lo tanto,$\displaystyle \lim_{x→∞}x^3=∞$. Por otro lado, as$x→−∞$, los valores de$f(x)=x^3$ son negativos pero llegan a ser arbitrariamente grandes en magnitud. En consecuencia,$\displaystyle \lim_{x→−∞}x^3=−∞.$

Tabla$\PageIndex{2}$: Valores de una función de potencia como$x→±∞$
$x$	10	20	50	100	1000
$x^3$	1000	8000	125,000	1,000,000	1,000,000,000
$x$	−10	−20	−50	−100	−1000
$x^3$	−1000	−8000	−125.000	−1,000,000	−1,000,000,000

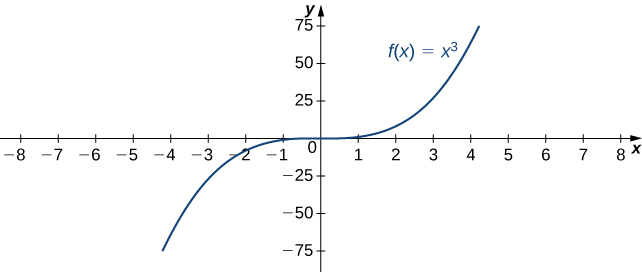
Se grafica la función f (x) = x3. Es evidente que esta función se acerca rápidamente al infinito a medida que x se acerca al infinito. — Figura$\PageIndex{8}$: Para esta función, los valores funcionales se acercan al$±$ infinito como$x→±∞.$

Definición: Límite Infinito en el Infinito (Informal)

Decimos que una función$f$ tiene un límite infinito en el infinito y escribimos

\[\lim_{x→∞}f(x)=∞. \nonumber \]

si$f(x)$ se vuelve arbitrariamente grande para$x$ suficientemente grande. Decimos que una función tiene un límite infinito negativo en el infinito y escribimos

\[\lim_{x→∞}f(x)=−∞. \nonumber \]

si$f(x)<0$ y$|f(x)|$ se vuelve arbitrariamente grande para$x$ suficientemente grande. Del mismo modo, podemos definir límites infinitos como$x→−∞.$

Definiciones formales

Anteriormente, utilizamos los términos arbitrariamente cerca, arbitrariamente grandes y suficientemente grandes para definir límites al infinito de manera informal. Aunque estos términos proporcionan descripciones precisas de los límites en el infinito, no son matemáticamente precisos. Aquí hay definiciones más formales de límites en el infinito. Luego analizamos cómo usar estas definiciones para probar resultados que involucran límites en el infinito.

Definición: Límite al infinito (Formal)

Decimos que una función$f$ tiene un límite al infinito, si existe un número real$L$ tal que para todos$ε>0$, existe$N>0$ tal que

\[|f(x)−L|<ε \nonumber \]

para todos$x>N.$ en ese caso, escribimos

\[\lim_{x→∞}f(x)=L \nonumber \]

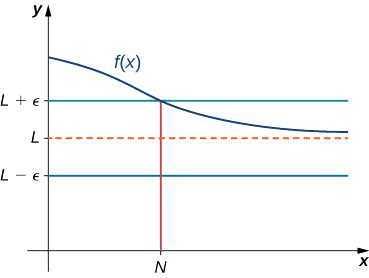
Se grafica la función f (x), y tiene una asíntota horizontal en L. L está marcada en el eje y, al igual que L + y L —. En el eje x, N se marca como el valor de x de tal manera que f (x) = L +. — Figura$\PageIndex{9}$: Para una función con límite al infinito, para todos$x>N, |f(x)−L|<ε.$

Anteriormente en esta sección, se utilizó evidencia gráfica en Figura$\PageIndex{1}$ y evidencia numérica en Tabla$\PageIndex{1}$ para concluir que$\displaystyle \lim_{x→∞}\left(2+\frac{1}{x}\right)=2$. Aquí utilizamos la definición formal de límite al infinito para probar rigurosamente este resultado.

Ejemplo$\PageIndex{2}$:

Utilizar la definición formal de límite al infinito para demostrarlo$\displaystyle \lim_{x→∞}\left(2+\frac{1}{x}\right)=2$.

Solución

Vamos$ε>0.$ a dejar$N=\frac{1}{ε}$. Por lo tanto, para todos$x>N$, tenemos

\[\left|2+\frac{1}{x}−2\right|=\left|\frac{1}{x}\right|=\frac{1}{x}<\frac{1}{N}=ε \nonumber \]

Ejercicio$\PageIndex{2}$

Utilizar la definición formal de límite al infinito para demostrarlo$\displaystyle \lim_{x→∞}\left(3-\frac{1}{x^2}\right)=3$.

Insinuación: Vamos$N=\frac{1}{\sqrt{ε}}$.

Contestar

Vamos$ε>0.$ a dejar$N=\frac{1}{\sqrt{ε}}$. Por lo tanto, por todo$x>N,$ lo que tenemos

\[\Big|3−\frac{1}{x^2}−3\Big|=\frac{1}{x^2}<\frac{1}{N^2}=ε \nonumber \]

Por lo tanto,$\displaystyle \lim_{x→∞}(3−1/x^2)=3.$

Ahora dirigimos nuestra atención a una definición más precisa para un límite infinito en el infinito.

Definición: Límite infinito en el infinito (Formal)

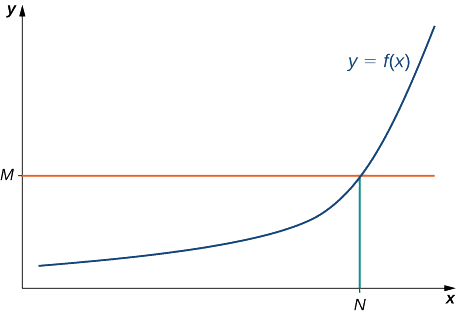
Decimos que una función$f$ tiene un límite infinito en el infinito y escribir

$\displaystyle \lim_{x→∞}f(x)=∞$

si por todos$M>0,$ existe$N>0$ tal que

$f(x)>M$

para todos$x>N$ (ver Figura$\PageIndex{10}$).

Decimos que una función tiene un límite infinito negativo en el infinito y escribimos

$\displaystyle \lim_{x→∞}f(x)=−∞$

si por todos$M<0$, existe$N>0$ tal que

$f(x)<M$

para todos$x>N$.

Del mismo modo podemos definir límites como$x→−∞.$

Se grafica la función f (x). Continúa aumentando rápidamente después de x = N, y f (N) = M. — Figura$\PageIndex{10}$: Para una función con un límite infinito en el infinito, para todos$x>N,\; f(x)>M.$

Anteriormente, se utilizó evidencia gráfica (Figura$\PageIndex{8}$) y evidencia numérica (Tabla$\PageIndex{2}$) para concluir que$\displaystyle \lim_{x→∞}x^3=∞$. Aquí utilizamos la definición formal de límite infinito al infinito para probar ese resultado.

Ejemplo$\PageIndex{3}$

Usa la definición formal de límite infinito en el infinito para demostrar que$\displaystyle \lim_{x→∞}x^3=∞.$

Solución

Vamos$M>0.$ a dejar$N=\sqrt[3]{M}$. Entonces, para todos$x>N$, tenemos

$x^3>N^3=(\sqrt[3]{M})^3=M.$

Por lo tanto,$\displaystyle \lim_{x→∞}x^3=∞$.

Ejercicio$\PageIndex{3}$

Usa la definición formal de límite infinito en el infinito para demostrar que$\displaystyle \lim_{x→∞}3x^2=∞.$

Insinuación: Vamos$N=\sqrt{\frac{M}{3}}$.

Contestar

Vamos$M>0.$ a dejar$N=\sqrt{\frac{M}{3}}$. Entonces, por todo$x>N,$ lo que tenemos

$3x^2>3N^2=3\left(\sqrt{\frac{M}{3}}\right)^2=\frac{3M}{3}=M$

Comportamiento final

El comportamiento de una función como$x→±∞$ se llama el comportamiento final de la función. En cada uno de los extremos de la función, la función podría exhibir uno de los siguientes tipos de comportamiento:

La función$f(x)$ se aproxima a una asíntota horizontal$y=L$.
La función$f(x)→∞$ o$f(x)→−∞.$
La función no se acerca a un límite finito, ni se acerca$∞$ ni$−∞$. En este caso, la función puede tener algún comportamiento oscilatorio.

Consideremos varias clases de funciones aquí y veamos los diferentes tipos de comportamientos finales para estas funciones.

Comportamiento final para funciones polinomiales

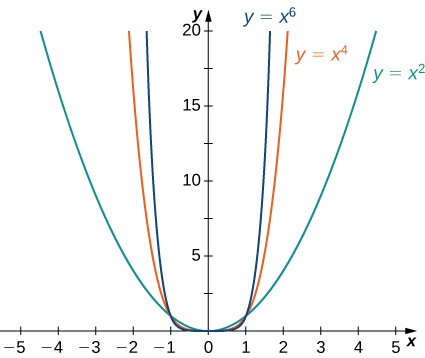
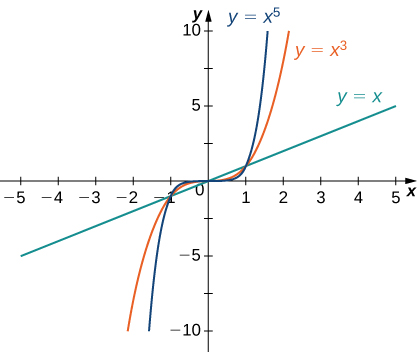
Considere la función power$f(x)=x^n$ donde$n$ es un entero positivo. De Figura$\PageIndex{11}$ y Figura$\PageIndex{12}$, vemos que

\[\lim_{x→∞}x^n=∞;\;n=1,2,3,… \nonumber \]

\[\lim_{x→−∞}x^n=\begin{cases}∞, & n=2,4,6,…\\−∞, & n=1,3,5,….\end{cases} \nonumber \]

Las funciones x2, x4 y x6 están graficadas, y es evidente que a medida que el exponente crece las funciones aumentan más rápidamente. — Figura$\PageIndex{11}$: Para funciones de potencia con una potencia uniforme$n$,$\displaystyle \lim_{x→∞}x^n=∞=\lim_{x→−∞}x^n$.

Se grafican las funciones x, x3 y x5, y es evidente que a medida que crece el exponente, las funciones aumentan más rápidamente. — Figura$\PageIndex{12}$: Para funciones de potencia con una potencia impar$n$,$\displaystyle \lim_{x→∞}x^n=∞$ y$\displaystyle \lim_{x→−∞}x^n=−∞.$

Utilizando estos hechos, no es difícil de evaluar$\displaystyle \lim_{x→∞}cx^n$ y$\displaystyle \lim_{x→−∞}cx^n$, donde$c$ está cualquier constante y$n$ es un entero positivo. Si$c>0$, la gráfica de$y=cx^n$ es un estiramiento vertical o compresión de$y=x^n,$ y por lo tanto

$\displaystyle \lim_{x→∞}cx^n=\lim_{x→∞}x^n$y$\displaystyle \lim_{x→−∞}cx^n=\lim_{x→−∞}x^n$ si$c>0$.

Si$c<0,$ la gráfica de$y=cx^n$ es un estiramiento vertical o compresión combinada con una reflexión alrededor del$x$ eje, y por lo tanto

$\displaystyle \lim_{x→∞}cx^n=−\lim_{x→∞}x^n$y$\displaystyle \lim_{x→−∞}cx^n=−\lim_{x→−∞}x^n$ si$c<0.$

Si$c=0,y=cx^n=0,$ en cuyo caso$\displaystyle \lim_{x→∞}cx^n=0=\lim_{x→−∞}cx^n.$

Ejemplo$\PageIndex{4}$: Limits at Infinity for Power Functions

Para cada función$f$, evaluar$\displaystyle \lim_{x→∞}f(x)$ y$\displaystyle \lim_{x→−∞}f(x)$.

$f(x)=−5x^3$
$f(x)=2x^4$

Solución

Dado que el coeficiente de$x^3$ es$−5$, la gráfica de$f(x)=−5x^3$ implica un estiramiento vertical y reflexión de la gráfica de$y=x^3$ alrededor del$x$ eje -eje. Por lo tanto,$\displaystyle \lim_{x→∞}(−5x^3)=−∞$ y$\displaystyle \lim_{x→−∞}(−5x^3)=∞$.
Dado que el coeficiente de$x^4$ es$2$, la gráfica de$f(x)=2x^4$ es un estiramiento vertical de la gráfica de$y=x^4$. Por lo tanto,$\displaystyle \lim_{x→∞}2x^4=∞$ y$\displaystyle \lim_{x→−∞}2x^4=∞$.

Ejercicio$\PageIndex{4}$

Vamos$f(x)=−3x^4$. Encuentra$\displaystyle \lim_{x→∞}f(x)$.

Insinuación: El coeficiente$−3$ es negativo.

Contestar: $−∞$

Ahora vemos cómo los límites en el infinito para las funciones de potencia se pueden usar$\displaystyle \lim_{x→±∞}f(x)$ para determinar para cualquier función polinómica$f$. Considerar una función polinómica

\[f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a^1x+a^0 \nonumber \]

de grado$n≥1$ para que$a_n≠0.$

Factoring, vemos que

\[f(x)=a_nx^n\left(1+\frac{a_{n−1}}{a_n}\frac{1}{x}+…+\frac{a_1}{a_n}\frac{1}{x^{n−1}}+\frac{a_0}{a_n}\frac{1}{x^n}\right). \nonumber \]

Como$x→±∞,$ todos los términos dentro de los paréntesis se acercan a cero excepto el primer término. Concluimos que

\[\lim_{x→±∞}f(x)=\lim_{x→±∞}a_nx^n. \nonumber \]

Por ejemplo, la función$f(x)=5x^3−3x^2+4$ se comporta$g(x)=5x^3$$x→±∞$ como se muestra en Figura$\PageIndex{13}$ y Tabla$\PageIndex{3}$.

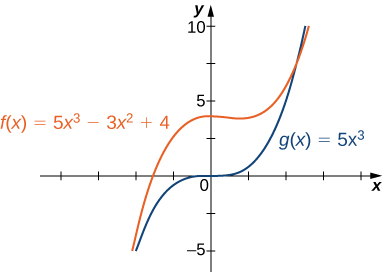
Se trazan ambas funciones f (x) = 5x3 — 3x2 + 4 y g (x) = 5x3. Su comportamiento para grandes números positivos y grandes negativos converge. — Figura$\PageIndex{13}$: El comportamiento final de un polinomio está determinado por el comportamiento del término con el mayor exponente.

Tabla$\PageIndex{3}$: El comportamiento final de un polinomio está determinado por el término con el mayor exponente
$x$	10	100	1000
$f(x)=5x^3−3x^2+4$	4704	4,970,004	4,997,000,004
$g(x)=5x^3$	5000	5,000,000	5,000,000,000
$x$	−10	−100	−000
$f(x)=5x^3−3x^2+4$	−5296	−5.029.996	−5,002,999,996
$g(x)=5x^3$	−5000	−5,000,000	−5,000,000,000

Comportamiento final para funciones algebraicas

El comportamiento final para funciones racionales y funciones que involucran radicales es un poco más complicado que para polinomios. En Ejemplo$\PageIndex{5}$, mostramos que los límites al infinito de una función racional$f(x)=\dfrac{p(x)}{q(x)}$ dependen de la relación entre el grado del numerador y el grado del denominador. Para evaluar los límites al infinito para una función racional, dividimos el numerador y el denominador por el poder más alto de$x$ aparecer en el denominador. Esto determina qué término en la expresión general domina el comportamiento de la función a grandes valores de$x$.

Ejemplo$\PageIndex{5}$: Determining End Behavior for Rational Functions

Para cada una de las siguientes funciones, determine los límites como$x→∞$ y$x→−∞.$ Luego, use esta información para describir el comportamiento final de la función.

$f(x)=\dfrac{3x−1}{2x+5}$(Nota: El grado del numerador y el denominador son los mismos.)
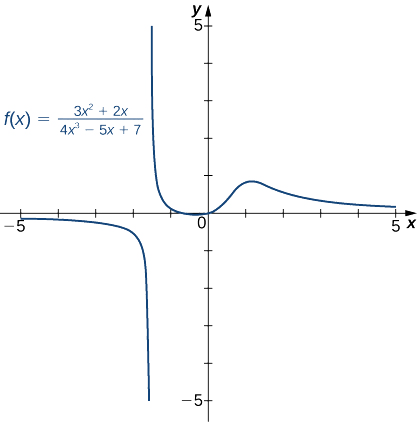
$f(x)=\dfrac{3x^2+2x}{4x^3−5x+7}$(Nota: El grado de numerador es menor que el grado del denominador.)
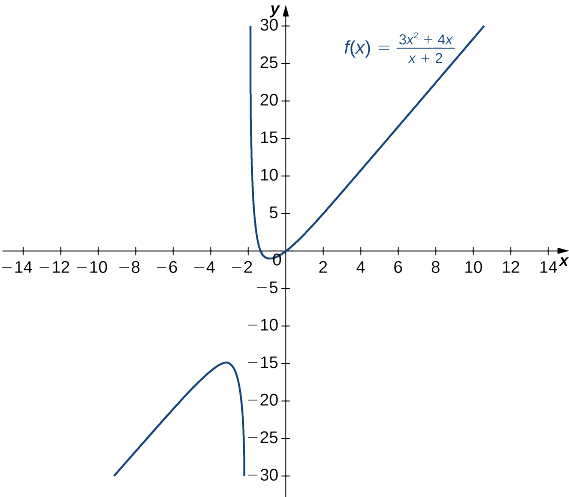
$f(x)=\dfrac{3x^2+4x}{x+2}$(Nota: El grado del numerador es mayor que el grado del denominador.)

Solución

a. El poder más alto de$x$ en el denominador es$x$. Por lo tanto, dividiendo el numerador y el denominador por$x$ y aplicando las leyes de límite algebraicas, vemos que

\[ \begin{align*} \lim_{x→±∞}\frac{3x−1}{2x+5} &=\lim_{x→±∞}\frac{3−1/x}{2+5/x} \\[4pt] &=\frac{\lim_{x→±∞}(3−1/x)}{\lim_{x→±∞}(2+5/x)} \\[4pt] &=\frac{\lim_{x→±∞}3−\lim_{x→±∞}1/x}{\lim_{x→±∞}2+\lim_{x→±∞}5/x} \\[4pt] &=\frac{3−0}{2+0}=\frac{3}{2}. \end{align*}\]

Ya que$\displaystyle \lim_{x→±∞}f(x)=\frac{3}{2}$, sabemos que$y=\frac{3}{2}$ es una asíntota horizontal para esta función como se muestra en la siguiente gráfica.

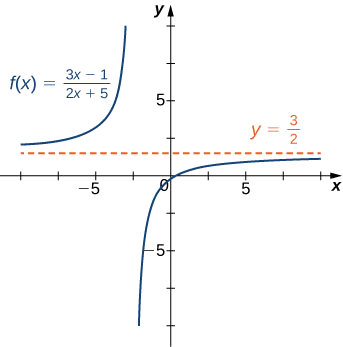
Un par de gráficas curvas. El primero comienza en el lado izquierdo de la figura, donde es casi plana con valor Y 3 sobre 2, luego se dobla a casi vertical, dejando la parte superior de la figura en X es igual a 5 mitades negativas. La otra curva se eleva casi verticalmente desde la parte inferior en X es igual a 5 mitades negativas, se nivela y se vuelve casi horizontal a la derecha con un valor Y cerca de 3 mitades — Figura$\PageIndex{14}$: La gráfica de esta función racional se aproxima a una asíntota horizontal como$x→±∞.$

b. Dado que el mayor poder de$x$ aparecer en el denominador es$x^3$, dividir el numerador y el denominador por$x^3$. Después de hacerlo y aplicar leyes de límite algebraico, obtenemos

\[\lim_{x→±∞}\frac{3x^2+2x}{4x^3−5x+7}=\lim_{x→±∞}\frac{3/x+2/x^2}{4−5/x^2+7/x^3}=\frac{3\cdot 0+2\cdot 0}{4−5\cdot 0+7\cdot 0}=\frac{0}{4}=0. \nonumber \]

Por lo tanto,$f$ tiene una asíntota horizontal de$y=0$ como se muestra en la siguiente gráfica.

La función f (x) = (3x2 + 2x)/(4x2 — 5x + 7) se traza como es su asíntota horizontal en y = 0. — Figura$\PageIndex{15}$: La gráfica de esta función racional se aproxima a la asíntota horizontal$y=0$ como$x→±∞.$

c. Dividiendo el numerador y el denominador por$x$, tenemos

\[\displaystyle \lim_{x→±∞}\frac{3x^2+4x}{x+2}=\lim_{x→±∞}\frac{3x+4}{1+2/x}. \nonumber \]

Como$x→±∞$, se acerca el denominador$1$. Como$x→∞$, se acerca el numerador$+∞$. Como$x→−∞$, se acerca el numerador$−∞$. Por lo tanto$\displaystyle \lim_{x→∞}f(x)=∞$, mientras que$\displaystyle \lim_{x→−∞}f(x)=−∞$ como se muestra en la siguiente figura.

Se grafica la función f (x) = (3x2 + 4x)/(x + 2). Parece tener una asíntota diagonal así como una asíntota vertical en x = −2. — Figura$\PageIndex{16}$: As$x→∞$, los valores$f(x)→∞$. Como$x→−∞$, los valores$f(x)→−∞.$

Ejercicio$\PageIndex{5}$

Evaluar$\displaystyle \lim_{x→±∞}\frac{3x^2+2x−1}{5x^2−4x+7}$ y utilizar estos límites para determinar el comportamiento final de$f(x)=\dfrac{3x^2+2x−1}{5x^2−4x+7}$.

Insinuación: Dividir el numerador y el denominador por$x^2$.

Contestar: $\frac{3}{5}$

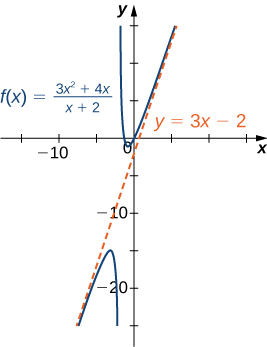
Antes de continuar, considere la gráfica de que$f(x)=\dfrac{3x^2+4x}{x+2}$ se muestra en la Figura$\PageIndex{16}$. Como$x→∞$ y$x→−∞$, la gráfica de$f$ aparece casi lineal. Aunque ciertamente no$f$ es una función lineal, ahora investigamos por qué la gráfica de$f$ parece estar acercándose a una función lineal. Primero, usando división larga de polinomios, podemos escribir

\[f(x)=\frac{3x^2+4x}{x+2}=3x−2+\frac{4}{x+2}. \nonumber \]

Ya que$\dfrac{4}{x+2}→0$ como$x→±∞,$ concluimos que

\[ \lim_{x→±∞}(f(x)−(3x−2))=\lim_{x→±∞}\frac{4}{x+2}=0. \nonumber \]

Por lo tanto, la gráfica de$f$ se acerca a la línea$y=3x−2$ como$x→±∞$. Esta línea es conocida como asíntota oblicua para$f$ (Figura$\PageIndex{17}$).

La función f (x) = (3x2 + 4x)/(x + 2) se traza como es su asíntota diagonal y = 3x — 2. — Figura$\PageIndex{17}$: La gráfica de la función racional$f(x)=(3x^2+4x)/(x+2)$ se aproxima a la asíntota oblicua$y=3x−2$ como$x→±∞.$

Podemos resumir los resultados de Ejemplo$\PageIndex{5}$ para hacer la siguiente conclusión con respecto al comportamiento final para funciones racionales. Considerar una función racional

\[f(x)=\frac{p(x)}{q(x)}=\frac{a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0}{b_mx^m+b_{m−1}x^{m−1}+…+b_1x+b_0},\nonumber \]

dónde$a_n≠0$ y$b_m≠0.$

Si el grado del numerador es el mismo que el grado del denominador$(n=m),$ entonces$f$ tiene una asíntota horizontal de$y=a_n/b_m$ como$x→±∞.$
Si el grado del numerador es menor que el grado del denominador$(n<m),$ entonces$f$ tiene una asíntota horizontal de$y=0$ as$x→±∞.$
Si el grado del numerador es mayor que el grado del denominador$(n>m),$ entonces$f$ no tiene una asíntota horizontal. Los límites en el infinito son infinitos positivos o negativos, dependiendo de los signos de los términos principales. Además, usando división larga, la función se puede reescribir como\[f(x)=\frac{p(x)}{q(x)}=g(x)+\frac{r(x)}{q(x)}, \nonumber \] donde el grado de$r(x)$ es menor que el grado de$q(x)$. Como resultado,$\displaystyle \lim_{x→±∞}r(x)/q(x)=0$. Por lo tanto, los valores de$[f(x)−g(x)]$ aproximación a cero como$x→±∞$. Si el grado de$p(x)$ es exactamente uno más que el grado de$q(x)$ (es decir,$n=m+1$), la función$g(x)$ es una función lineal. En este caso, llamamos$g(x)$ asíntota oblicua.

Ahora consideremos el comportamiento final para funciones que involucran a un radical.

Ejemplo$\PageIndex{6}$: Determining End Behavior for a Function Involving a Radical

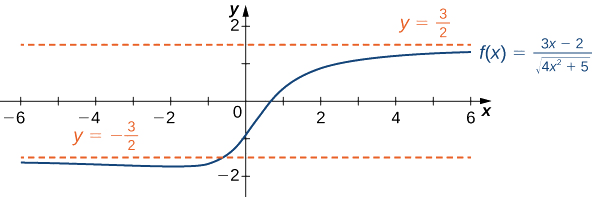
Encuentre los límites como$x→∞$ y$x→−∞$ para$f(x)=\dfrac{3x−2}{\sqrt{4x^2+5}}$ y describa el comportamiento final de$f$.

Solución

Usemos la misma estrategia que hicimos para las funciones racionales: dividir el numerador y el denominador por un poder de$x$. Para determinar el poder apropiado de$x$, considere la expresión$\sqrt{4x^2+5}$ en el denominador. Desde

\[\sqrt{4x^2+5}≈\sqrt{4x^2}=2|x| \nonumber \]

para grandes valores de$x$ en efecto$x$ aparece justo a la primera potencia en el denominador. Por lo tanto, dividimos el numerador y el denominador por$|x|$. Luego, usando el hecho de que$|x|=x$$x>0, |x|=−x$ para$x<0$, y$|x|=\sqrt{x^2}$ para todos$x$, calculamos los límites de la siguiente manera:

\ [\ begin {alinear*}\ lim_ {x→∞}\ frac {3x−2} {\ sqrt {4x^2+5}} &=\ lim_ {x→∞}\ frac {(1/|x|) (3x−2)} {(1/|x|)\ sqrt {4x^2+5}}\\ [4pt]
&=\ lim_ {x→∞}\ frac {(1/x) (3x−2)} {\ sqrt {(1/x^2) (4x^2+5)}}\\ [4pt]
&=\ lim_ {x→∞}\ frac {3−2/x} {\ sqrt {4+5/x^2}} =\ frac {3} {\ sqrt {4}} =\ frac {3} 2}\ final {alinear*}\]

\ [\ begin {alinear*}\ lim_ {x→−∞}\ frac {3x−2} {\ sqrt {4x^2+5}} &=\ lim_ {x→−∞}\ frac {(1/|x|) (3x−2)} {(1/|x|)\ sqrt {4x^2+5}}\\ [4pt]
&=\ lim_ {x→→→−∞}\ frac {(−1/x) (3x−2)} {\ sqrt {(1/x^2) (4x^2+5)}}\\ [4pt]
&=\ lim_ {x→−∞}\ frac {−3+2/x} {\ sqrt {4+5/x^2}} =\ frac {−3} {\ sqrt {4}} =\ frac {−3} {2}. \ end {alinear*}\]

Por lo tanto,$f(x)$ se acerca a la asíntota horizontal$y=\frac{3}{2}$ como$x→∞$ y a la asíntota horizontal$y=−\frac{3}{2}$$x→−∞$ como se muestra en la siguiente gráfica.

Se traza la función f (x) = (3x − 2)/(la raíz cuadrada de la cantidad (4x2 + 5)). Tiene dos asíntotas horizontales a y = ±3/2, y cruza y = −3/2 antes de converger hacia ella desde abajo. — Figura$\PageIndex{18}$: Esta función tiene dos asíntotas horizontales y cruza una de las asíntotas.

Ejercicio$\PageIndex{6}$

Evaluar$\displaystyle \lim_{x→∞}\frac{\sqrt{3x^2+4}}{x+6}$.

Insinuación: Dividir el numerador y el denominador por$x$.

Contestar: $\sqrt{3}$

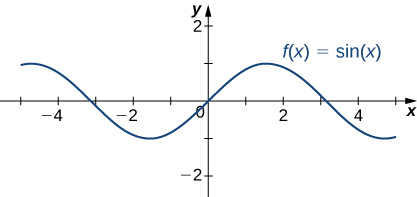
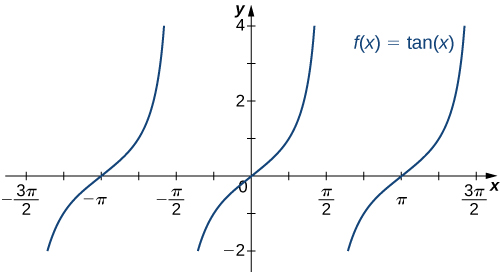
Determinación del Comportamiento Final para Funciones Trascendentales

Las seis funciones trigonométricas básicas son periódicas y no se acercan a un límite finito ya que$x→±∞.$ Por ejemplo,$\sin x$ oscila entre 1 y −1 (Figura$\PageIndex{19}$). La función tangente$x$ tiene un número infinito de asíntotas verticales ya que$x→±∞$; por lo tanto, no se acerca a un límite finito ni se acerca$±∞$$x→±∞$ como se muestra en la Figura$\PageIndex{20}$.

Se grafica la función f (x) = sin x. — Figura$\PageIndex{19}$: La función$f(x)=\sin x$ oscila entre$1$ y$−1$ como$x→±∞$

Se grafica la función f (x) = tan x. — Figura$\PageIndex{20}$: La función$f(x)=\tan x$ no se acerca a un límite y no se acerca$±∞$ como$x→±∞$

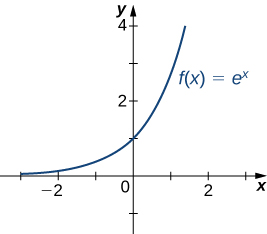
Recordemos que para cualquier base$b>0,\; b≠1,$ la función$y=b^x$ es una función exponencial con dominio$(−∞,∞)$ y rango$(0,∞)$. Si$b>1,\;y=b^x$ está aumentando sobre$(−∞,∞)$. Si$0<b<1, \; y=b^x$ es decreciente sobre$(−∞,∞).$ Para la función exponencial natural$f(x)=e^x, \; e≈2.718>1$. Por lo tanto,$f(x)=e^x$ está aumentando$(−∞,∞)$ y el rango es$(0,∞)$. La función exponencial$f(x)=e^x$ se aproxima$∞$ como$x→∞$ y se aproxima$0$$x→−∞$ como se muestra en Tabla$\PageIndex{4}$ y Figura$\PageIndex{21}$.

Tabla$\PageIndex{4}$: Comportamiento final de la función exponencial natural
$x$	−5	−2	0	2	5
$e^x$	0.00674	0.135	1	7.389	148.413

Se grafica la función f (x) = ex. — Figura$\PageIndex{21}$: La función exponencial se aproxima a cero como$x→−∞$ y se acerca$∞$ como$x→∞.$

Recordemos que la función logaritmo natural$f(x)=\ln(x)$ es la inversa de la función exponencial natural$y=e^x$. Por lo tanto, el dominio de$f(x)=\ln(x)$ es$(0,∞)$ y el rango es$(−∞,∞)$. La gráfica de$f(x)=\ln(x)$ es el reflejo de la gráfica de$y=e^x$ alrededor de la línea$y=x$. Por lo tanto,$\ln(x)→−∞$ como$x→0^+$ y$\ln(x)→∞$$x→∞$ como se muestra en la Figura$\PageIndex{22}$ y Tabla$\PageIndex{5}$.

Tabla$\PageIndex{5}$: Comportamiento final de la función logaritmo natural
$x$	0.01	0.1	1	10	100
$\ln(x)$	−4.605	−2.303	0	2.303	4.605

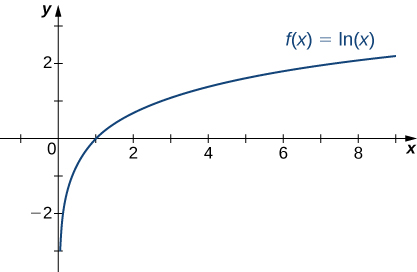
Se grafica la función f (x) = ln (x). — Figura$\PageIndex{22}$: La función logaritmo natural se aproxima$∞$ como$x→∞.$

Ejemplo$\PageIndex{7}$: Determining End Behavior for a Transcendental Function

Encuentre los límites como$x→∞$ y$x→−∞$ para$f(x)=\dfrac{2+3e^x}{7−5e^x}$ y describa el comportamiento final de$f.$

Solución

Para encontrar el límite como$x→∞,$ dividir el numerador y denominador por$e^x$:

\[ \begin{align*} \lim_{x→∞}f(x) &= \lim_{x→∞}\frac{2+3e^x}{7−5e^x} \\[4pt] &=\lim_{x→∞}\frac{(2/e^x)+3}{(7/e^x)−5.} \end{align*}\]

Como se muestra en la Figura$\PageIndex{21}$,$e^x→∞$ como$x→∞$. Por lo tanto,

$\displaystyle \lim_{x→∞}\frac{2}{e^x}=0=\lim_{x→∞}\frac{7}{e^x}$.

Se concluye que$\displaystyle \lim_{x→∞}f(x)=−\frac{3}{5}$, y la gráfica de$f$ se acerca a la asíntota horizontal$y=−\frac{3}{5}$ como$x→∞.$ Para encontrar el límite como$x→−∞$, utilizar el hecho de que$e^x→0$ como$x→−∞$ para concluir que$\displaystyle \lim_{x→-∞}f(x)=\frac{2}{7}$, y por lo tanto la gráfica de$f(x)$ se acerca a la asíntota horizontal $y=\frac{2}{7}$como$x→−∞$.

Ejercicio$\PageIndex{7}$

Encuentra los límites como$x→∞$ y$x→−∞$ para$f(x)=\dfrac{3e^x−4}{5e^x+2}$.

Insinuación: $\displaystyle \lim_{x→∞}e^x=∞$y$\displaystyle \lim_{x→-∞}e^x=0.$

Contestar: $\displaystyle \lim_{x→∞}f(x)=\frac{3}{5}, \quad\lim_{x→−∞}f(x)=−2$

Lineamientos para Dibujar la Gráfica de una Función

Ahora contamos con suficientes herramientas analíticas para dibujar gráficas de una amplia variedad de funciones algebraicas y trascendentales. Antes de mostrar cómo graficar funciones específicas, veamos una estrategia general para usar al graficar cualquier función.

Estrategia de resolución de problemas: dibujo de la gráfica de una función

Dada una función$f$, utilice los siguientes pasos para esbozar una gráfica de$f$:

Determinar el dominio de la función.
Localice las intercepciones$x$ - y$y$ -intercepciones.
$\displaystyle \lim_{x→−∞}f(x)$Evaluar$\displaystyle \lim_{x→∞}f(x)$ y determinar el comportamiento final. Si alguno de estos límites es un número finito$L$, entonces$y=L$ es una asíntota horizontal. Si alguno de estos límites es$∞$ o$−∞$, determinar si$f$ tiene una asíntota oblicua. Si$f$ es una función racional tal que$f(x)=\dfrac{p(x)}{q(x)}$, donde el grado del numerador es mayor que el grado del denominador, entonces se$f$ puede escribir como\[f(x)=\frac{p(x)}{q(x)}=g(x)+\frac{r(x)}{q(x),} \nonumber \] donde el grado de$r(x)$ es menor que el grado de$q(x)$. Los valores de$f(x)$ aproximación a los valores de$g(x)$ as$x→±∞$. Si$g(x)$ es una función lineal, se le conoce como asíntota oblicua.
Determinar si$f$ tiene alguna asíntota vertical.
Calcular$f′.$ Encuentra todos los puntos críticos y determina los intervalos donde$f$ esta aumentando y donde$f$ esta disminuyendo. Determinar si$f$ tiene algún extremo local.
Calcular$f''.$ Determine los intervalos donde$f$ es cóncavo hacia arriba y dónde$f$ es cóncavo abajo Utilice esta información para determinar si$f$ tiene algún punto de inflexión. La segunda derivada también se puede utilizar como medio alternativo para determinar o verificar que$f$ tiene un extremo local en un punto crítico.

Ahora usemos esta estrategia para graficar varias funciones diferentes. Comenzamos por graficar una función polinómica.

Ejemplo$\PageIndex{8}$: Sketching a Graph of a Polynomial

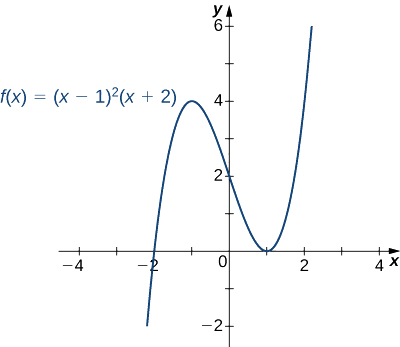
Esbozar un gráfico de$f(x)=(x−1)^2(x+2).$

Solución

Paso 1: Como$f$ es un polinomio, el dominio es el conjunto de todos los números reales.

Paso 2: Cuando$x=0,\; f(x)=2.$ Por lo tanto, la$y$ -intercepción es$(0,2)$. Para encontrar las$x$ -intercepciones, necesitamos resolver la ecuación$(x−1)^2(x+2)=0$, que nos da las$x$ -intercepciones$(1,0)$ y$(−2,0)$

Paso 3: Necesitamos evaluar el comportamiento final de$f.$ As$x→∞, \;(x−1)^2→∞$ y$(x+2)→∞$. Por lo tanto,$\displaystyle \lim_{x→∞}f(x)=∞$.

Como$x→−∞, \;(x−1)^2→∞$ y$(x+2)→−∞$. Por lo tanto,$\displaystyle \lim_{x→-∞}f(x)=−∞$.

Para obtener aún más información sobre el comportamiento final de$f$, podemos multiplicar los factores de$f$. Al hacerlo, vemos que

\[f(x)=(x−1)^2(x+2)=x^3−3x+2. \nonumber \]

Dado que el término principal de$f$ es$x^3$, concluimos que$f$ se comporta$y=x^3$ como$x→±∞.$

Paso 4: Dado que$f$ es una función polinómica, no tiene asíntotas verticales.

Paso 5: La primera derivada de$f$ es

\[f′(x)=3x^2−3. \nonumber \]

Por lo tanto,$f$ tiene dos puntos críticos:$x=1,−1.$ Dividir el intervalo$(−∞,∞)$ en los tres intervalos más pequeños:$(−∞,−1), \;(−1,1)$, y$(1,∞)$. Después, elija los puntos de prueba$x=−2, x=0$, y$x=2$ a partir de estos intervalos y evalúe el signo de$f′(x)$ en cada uno de estos puntos de prueba, como se muestra en la siguiente tabla.

Intervalo	Punto de prueba	Signo de Derivada$f'(x)=3x^2−3=3(x−1)(x+1)$	Conclusión
$(−∞,−1)$	$x=−2$	\ (f' (x) =3x^2−3=3 (x−1) (x+1)\)” style="text-align:center; ">$(+)(−)(−)=+$	$f$está aumentando
$(−1,1)$	$x=0$	\ (f' (x) =3x^2−3=3 (x−1) (x+1)\)” style="text-align:center; ">$(+)(−)(+)=−$	$f$decreciente
$(1,∞)$	$x=2$	\ (f' (x) =3x^2−3=3 (x−1) (x+1)\)” style="text-align:center; ">$(+)(+)(+)=+$	$f$está aumentando

De la mesa, vemos que$f$ tiene un máximo local en$x=−1$ y un mínimo local en$x=1$. Evaluando$f(x)$ en esos dos puntos, encontramos que el valor máximo local es$f(−1)=4$ y el valor mínimo local es$f(1)=0.$

Paso 6: La segunda derivada de$f$ es

\[f''(x)=6x. \nonumber \]

La segunda derivada es cero en$x=0.$ Por lo tanto, para determinar la concavidad de$f$, dividir el intervalo$(−∞,∞)$ en los intervalos más pequeños$(−∞,0)$ y$(0,∞)$, y elegir puntos de prueba$x=−1$ y$x=1$ determinar la concavidad de$f$ en cada uno de estos intervalos más pequeños como se muestra en la siguiente tabla.

Intervalo	Punto de prueba	Signo de$f''(x)=6x$	Conclusión
$(−∞,0)$	$x=−1$	\ (f "(x) =6x\)” style="text-align:center; ">$−$	$f$es cóncavo hacia abajo.
$(0,∞)$	$x=1$	\ (f "(x) =6x\)” style="text-align:center; ">$+$	$f$es cóncavo hacia arriba.

Observamos que la información de la tabla anterior confirma el hecho, encontrado en paso$5$, de que f tiene un máximo local en$x=−1$ y un mínimo local en$x=1$. Además, la información encontrada en el paso$5$ —es decir,$f$ tiene un máximo local en$x=−1$ y un mínimo local en$x=1$, y$f′(x)=0$ en esos puntos— combinada con el hecho de que$f''$ los cambios se firman solo en$x=0$ confirma los resultados encontrados en paso$6$ sobre el concavidad de$f$.

Combinando esta información, llegamos a la gráfica de que$f(x)=(x−1)^2(x+2)$ se muestra en la siguiente gráfica.

$Se grafica la función f (x) = (x −1) 2 (x + 2). Cruza el eje x en x = −2 y toca el eje x en x = 1.$

Ejercicio$\PageIndex{8}$

Esbozar un gráfico de$f(x)=(x−1)^3(x+2).$

Insinuación: $f$es un polinomio de cuarto grado.
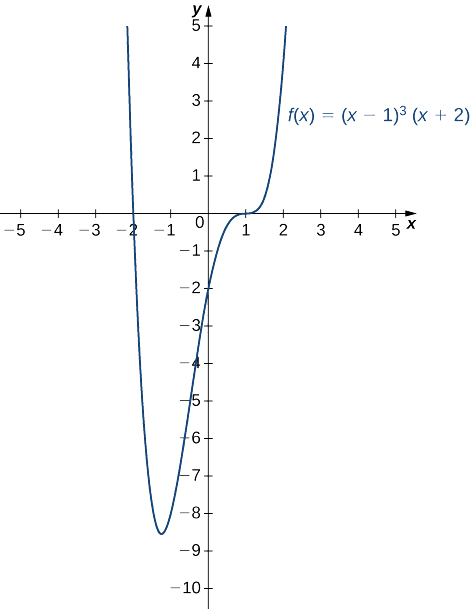
Contestar: $Se grafica la función f (x) = (x −1) 3 (x + 2).$

Ejemplo$\PageIndex{9}$: Sketching a Rational Function

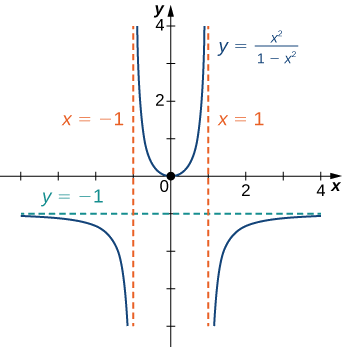
Esbozar la gráfica de$f(x)=\dfrac{x^2}{1−x^2}$.

Solución

Paso 1: La función$f$ se define siempre y cuando el denominador no sea cero. Por lo tanto, el dominio es el conjunto de todos los números reales$x$ excepto$x=±1.$

Paso 2: Encuentra las intercepciones. Si$x=0,$ entonces$f(x)=0$, también lo$0$ es una intercepción. Si$y=0$, entonces$\dfrac{x^2}{1−x^2}=0,$ lo que implica$x=0$. Por lo tanto,$(0,0)$ es la única intercepción.

Paso 3: Evaluar los límites al infinito. Dado que$f$ es una función racional, dividir el numerador y denominador por el poder más alto en el denominador:$x^2$ .Obtenemos

$\displaystyle \lim_{x→±∞}\frac{x^2}{1−x^2}=\lim_{x→±∞}\frac{1}{\frac{1}{x^2}−1}=−1.$

Por lo tanto,$f$ tiene una asíntota horizontal de$y=−1$ as$x→∞$ y$x→−∞.$

Paso 4: Para determinar si$f$ tiene alguna asíntota vertical, primero verifique si el denominador tiene algún cero. Encontramos que el denominador es cero cuando$x=±1$. Determinar si las líneas$x=1$ o$x=−1$ son asíntotas verticales de$f$, evaluar$\displaystyle \lim_{x→1}f(x)$ y$\displaystyle \lim_{x→−1}f(x)$. Al mirar cada límite unilateral como$x→1,$ vemos que

$\displaystyle \lim_{x→1^+}\frac{x^2}{1−x^2}=−∞$y$\displaystyle \lim_{x→1^−}\frac{x^2}{1−x^2}=∞.$

Además, al observar cada límite unilateral ya que$x→−1,$ encontramos que

$\displaystyle \lim_{x→−1^+}\frac{x^2}{1−x^2}=∞$y$\displaystyle \lim_{x→−1^−}\frac{x^2}{1−x^2}=−∞.$

Paso 5: Calcular la primera derivada:

$f′(x)=\dfrac{(1−x^2)(2x)−x^2(−2x)}{\Big(1−x^2\Big)^2}=\dfrac{2x}{\Big(1−x^2\Big)^2}$.

Los puntos críticos ocurren en puntos$x$ donde$f′(x)=0$ o$f′(x)$ es indefinido. Vemos que$f′(x)=0$ cuando$x=0.$ La derivada no$f′$ está indefinida en ningún momento del dominio de$f$. Sin embargo, no$x=±1$ están en el dominio de$f$. Por lo tanto, para determinar dónde$f$ está aumentando y dónde$f$ está disminuyendo, divida el intervalo$(−∞,∞)$ en cuatro intervalos más pequeños:$(−∞,−1), (−1,0), (0,1),$ y$(1,∞)$, y elija un punto de prueba en cada intervalo para determinar el signo de$f′(x)$ en cada uno de estos intervalos. Los valores$x=−2,\; x=−\frac{1}{2}, \;x=\frac{1}{2}$, y$x=2$ son buenas opciones para los puntos de prueba como se muestra en la siguiente tabla.

Intervalo	Punto de prueba	Signo de$f′(x)=\frac{2x}{(1−x^2)^2}$	Conclusión
$(−∞,−1)$	$x=−2$	\ (f′ (x) =\ frac {2x} {(1−x^2) ^2}\)” style="text-align:center; ">$−/+=−$	$f$está disminuyendo.
$(−1,0)$	$x=−1/2$	\ (f′ (x) =\ frac {2x} {(1−x^2) ^2}\)” style="text-align:center; ">$−/+=−$	$f$está disminuyendo.
$(0,1)$	$x=1/2$	\ (f′ (x) =\ frac {2x} {(1−x^2) ^2}\)” style="text-align:center; ">$+/+=+$	$f$va en aumento.
$(1,∞)$	$x=2$	\ (f′ (x) =\ frac {2x} {(1−x^2) ^2}\)” style="text-align:center; ">$+/+=+$	$f$va en aumento.

A partir de este análisis, se concluye que$f$ tiene un mínimo local$x=0$ pero no un máximo local.

Paso 6: Calcular la segunda derivada:

\ [\ begin {align*} f "(x) &=\ frac {(1−x^2) ^2 (2) −2x (2 (1−x^2) (−2x))} {(1−x^2) ^4}\\ [4pt]
&=\ frac {(1−x^2) [2 (1−x^2) +8x^2]}\ Grande (1−x^2\ Grande) ^4}\\ [4pt]
&=\ frac {2 (1−x^2) +8x^2} {\ Grande (1−x^2\ Grande) ^3}\\ [4pt]
&=\ frac {6x^2+2} {\ Grande (1−x^2\ Grande) ^3}. \ end {alinear*}\]

Para determinar los intervalos donde$f$ es cóncavo hacia arriba y dónde$f$ es cóncavo hacia abajo, primero necesitamos encontrar todos los puntos$x$ donde$f''(x)=0$ o$f''(x)$ es indefinido. Ya que el numerador$6x^2+2≠0$ para cualquiera nunca$x, f''(x)$ es cero. Además, no$f''$ está indefinido para ninguno$x$ en el dominio de$f$. Sin embargo, como se discutió anteriormente, no$x=±1$ están en el dominio de$f$. Por lo tanto, para determinar la concavidad de$f$, dividimos el intervalo$(−∞,∞)$ en los tres intervalos más pequeños$(−∞,−1), \, (−1,1)$, y$(1,∞)$, y elegimos un punto de prueba en cada uno de estos intervalos para evaluar el signo de$f''(x)$. Los valores$x=−2, \;x=0$, y$x=2$ son posibles puntos de prueba como se muestra en la siguiente tabla.

Intervalo	Punto de prueba	Signo de$f''(x)=\frac{6x^2+2}{(1−x^2)^3}$	Conclusión
$(−∞,−1)$	$x=−2$	\ (f "(x) =\ frac {6x^2+2} {(1−x^2) ^3}\)” style="text-align:center; ">$+/−=−$	$f$es cóncavo hacia abajo.
$(−1,1)$	$x=0$	\ (f "(x) =\ frac {6x^2+2} {(1−x^2) ^3}\)” style="text-align:center; ">$+/+=+$	$f$es cóncavo hacia arriba
$(1,∞)$	$x=2$	\ (f "(x) =\ frac {6x^2+2} {(1−x^2) ^3}\)” style="text-align:center; ">$+/−=−$	$f$es cóncavo hacia abajo.

Combinando toda esta información, llegamos a la gráfica de que$f$ se muestra a continuación. Tenga en cuenta que, aunque$f$ cambia la concavidad en$x=−1$ y$x=1$, no hay puntos de inflexión en ninguno de estos lugares porque no$f$ es continuo en$x=−1$ o$x=1.$

$Gráfica con 3 piezas. El más a la izquierda comienza a lo largo de una asíntota horizontal en Y es igual a 1 negativo en el lado izquierdo de la gráfica y se dobla hacia abajo a una asíntota vertical en X es igual a 1 negativo. La pieza media es vagamente parabólica, cayendo desde la parte superior de la gráfica en X equivale a 1 negativo al origen y luego se eleva de nuevo a la parte superior en X es igual a 1. La tercera pieza se eleva desde abajo en X es igual a 1 y se dobla para llegar al lado derecho a lo largo de una asíntota horizontal de Y es igual a 1 negativo.$

Ejercicio$\PageIndex{9}$

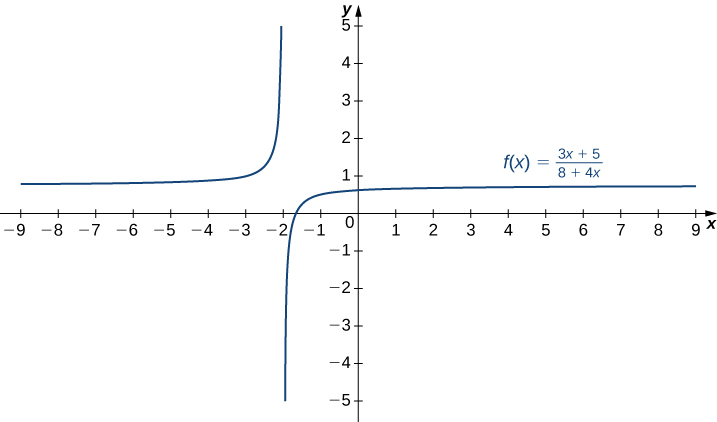
Esbozar un gráfico de$f(x)=\dfrac{3x+5}{8+4x}.$

Pista: Una línea$y=L$ es una asíntota horizontal de$f$ si el límite como$x→∞$ o el límite a partir$x→−∞$ de$f(x)$ es$L$. Una línea$x=a$ es una asíntota vertical si al menos uno de los límites unilaterales de$f$ como$x→a$ es$∞$ o$−∞.$

Contestar: $Se grafica la función f (x) = (3x + 5)/(8 + 4x). Parece tener asíntotas en x = −2 e y = 1.$

Ejemplo$\PageIndex{10}$: Sketching a Rational Function with an Oblique Asymptote

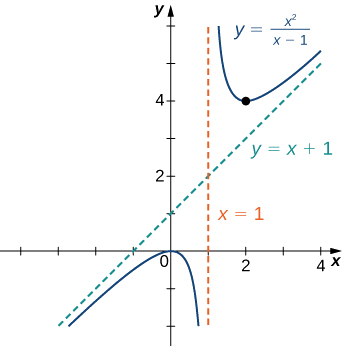
Esbozar el gráfico de$f(x)=\dfrac{x^2}{x−1}$

Solución

Paso 1: El dominio de$f$ es el conjunto de todos los números reales$x$ excepto$x=1.$

Paso 2: Encuentra las intercepciones. Podemos ver que cuando$x=0, \,f(x)=0,$ así$(0,0)$ es la única intercepción.

Paso 3: Evaluar los límites al infinito. Dado que el grado del numerador es uno más que el grado del denominador,$f$ debe tener una asíntota oblicua. Para encontrar la asíntota oblicua, utilice la división larga de polinomios para escribir

$f(x)=\dfrac{x^2}{x−1}=x+1+\dfrac{1}{x−1}$.

Ya que$\dfrac{1}{x−1}→0$ como$x→±∞, f(x)$ se acerca a la línea$y=x+1$ como$x→±∞$. La línea$y=x+1$ es una asíntota oblicua para$f$.

Paso 4: Para verificar si hay asíntotas verticales, mira donde el denominador es cero. Aquí el denominador es cero en$x=1.$ Mirando ambos límites unilaterales como$x→1,$ encontramos

$\displaystyle \lim_{x→1^+}\frac{x^2}{x−1}=∞$y$\displaystyle \lim_{x→1^−}\frac{x^2}{x−1}=−∞.$

Por lo tanto,$x=1$ es una asíntota vertical, y hemos determinado el comportamiento de$f$ como$x$ enfoques$1$ desde la derecha y la izquierda.

Paso 5: Calcular la primera derivada:

$f′(x)=\dfrac{(x−1)(2x)−x^2(1)}{(x−1)^2}=\dfrac{x^2−2x}{(x−1)^2}.$

Tenemos$f′(x)=0$ cuando$x^2−2x=x(x−2)=0$. Por lo tanto,$x=0$ y$x=2$ son puntos críticos. Dado que$f$ es indefinido en$x=1$, necesitamos dividir el intervalo$(−∞,∞)$ en los intervalos más pequeños$(−∞,0), (0,1), (1,2),$ y$(2,∞)$, y elegir un punto de prueba de cada intervalo para evaluar el signo de$f′(x)$ en cada uno de estos intervalos más pequeños. Por ejemplo, let$x=−1, x=\frac{1}{2}, x=\frac{3}{2}$, y$x=3$ ser los puntos de prueba como se muestra en la siguiente tabla.

Intervalo	Punto de prueba	Signo de$f'(x)=\dfrac{x^2−2x}{(x−1)^2}$	Conclusión
$(−∞,0)$	$x=−1$	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)” datos-valign="top"> (−) (−) /+=+	$f$va en aumento.
$(0,1)$	$x=1/2$	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)” datos-valign="top"> (+) (−) /+=−	$f$está disminuyendo.
$(1,2)$	$x=3/2$	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)” datos-valign="top"> (+) (−) /+=−	$f$está disminuyendo.
$(2,∞)$	$x=3$	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)” valign="top"> (+) (+) /+=+	$f$va en aumento.

De esta mesa, vemos que$f$ tiene un máximo local en$x=0$ y un mínimo local en$x=2$. El valor de$f$ al máximo local es$f(0)=0$ y el valor de$f$ al mínimo local es$f(2)=4$. Por lo tanto,$(0,0)$ y$(2,4)$ son puntos importantes en la gráfica.

Paso 6. Calcular la segunda derivada:

\ [\ begin {align*} f "(x) &=\ frac {(x−1) ^2 (2x−2) −2 (x−1) (x^2−2x)} {(x−1) ^4}\\ [4pt]
&=\ frac {2 (x−1) [(x−1) ^2− (x^2−2x)]} {(−1) ^4}\\ [4pt]
&=\ frac {2 [x^2-2x+1−x^2+2x]} {(x−1) ^3}\\ [4pt]
&=\ frac {2} {(x−1) ^3}. \ end {alinear*}\]

Vemos que nunca$f''(x)$ es cero o indefinido para$x$ en el dominio de$f$. Ya que$f$ es indefinido en$x=1$, para verificar la concavidad simplemente dividimos el intervalo$(−∞,∞)$ en los dos intervalos más pequeños$(−∞,1)$ y$(1,∞)$, y elegimos un punto de prueba de cada intervalo para evaluar el signo de$f''(x)$ en cada uno de estos intervalos. Los valores$x=0$ y$x=2$ son posibles puntos de prueba como se muestra en la siguiente tabla.

Intervalo	Punto de prueba	Signo de$f''(x)=\dfrac{2}{(x−1)^3}$	Conclusión
$(−∞,1)$	$x=0$	\ (f "(x) =\ dfrac {2} {(x−1) ^3}\)” style="text-align:center; ">$+/−=−$	$f$es cóncavo hacia abajo.
$(1,∞)$	$x=2$	\ (f "(x) =\ dfrac {2} {(x−1) ^3}\)” style="text-align:center; ">$+/+=+$	$f$es cóncavo hacia arriba

De la información recopilada, llegamos a la siguiente gráfica para$f.$

$Se grafica la función f (x) = x2/ (x − 1). Tiene asíntotas y = x + 1 y x = 1.$

Ejercicio$\PageIndex{10}$

Encuentra la asíntota oblicua para$f(x)=\dfrac{3x^3−2x+1}{2x^2−4}$.

Insinuación: Usar división larga de polinomios.

Contestar: $y=\frac{3}{2}x$

Ejemplo$\PageIndex{11}$: Sketching the Graph of a Function with a Cusp

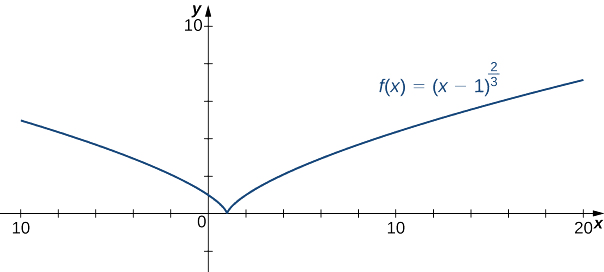
Esbozar un gráfico de$f(x)=(x−1)^{2/3}$

Solución

Paso 1: Dado que la función de raíz de cubo está definida para todos los números reales$x$ y$(x−1)^{2/3}=(\sqrt[3]{x−1})^2$, el dominio de$f$ es todos los números reales.

Paso 2: Para encontrar la$y$ -intercepción, evalúe$f(0)$. Ya que$f(0)=1,$ la$y$ -intercepción es$(0,1)$. Para encontrar la$x$ -intercepción, resolver$(x−1)^{2/3}=0$. La solución de esta ecuación es$x=1$, entonces la$x$ -intercepción es$(1,0).$

Paso 3: Dado que$\displaystyle \lim_{x→±∞}(x−1)^{2/3}=∞,$ la función sigue creciendo sin ataduras como$x→∞$ y$x→−∞.$

Paso 4: La función no tiene asíntotas verticales.

Paso 5: Para determinar dónde$f$ está aumentando o disminuyendo,$f′.$ calculamos Encontramos

\[f′(x)=\frac{2}{3}(x−1)^{−1/3}=\frac{2}{3(x−1)^{1/3}} \nonumber \]

Esta función no es cero en ninguna parte, pero es indefinida cuando$x=1.$ Por lo tanto, el único punto crítico es$x=1.$ Dividir el intervalo$(−∞,∞)$ en los intervalos más pequeños$(−∞,1)$ y$(1,∞)$, y elegir puntos de prueba en cada uno de estos intervalos para determinar el signo de$f′(x)$ en cada uno de estos intervalos más pequeños. Dejar$x=0$ y$x=2$ ser los puntos de prueba como se muestra en la siguiente tabla.

Intervalo	Punto de prueba	Signo de$f′(x)=\frac{2}{3(x−1)^{1/3}}$	Conclusión
$(−∞,1)$	$x=0$	\ (f′ (x) =\ frac {2} {3 (x−1) ^ {1/3}}\)” style="text-align:center; ">$+/−=−$	$f$está disminuyendo
$(1,∞)$	$x=2$	\ (f′ (x) =\ frac {2} {3 (x−1) ^ {1/3}}\)” style="text-align:center; ">$+/+=+$	$f$está aumentando

Concluimos que$f$ tiene un mínimo local en$x=1$. Evaluando$f$ en$x=1$, encontramos que el valor de$f$ al mínimo local es cero. Tenga en cuenta que no$f′(1)$ está definido, por lo que para determinar el comportamiento de la función en este punto crítico, necesitamos examinar$\displaystyle \lim_{x→1}f′(x).$ Mirando los límites unilaterales, tenemos

\[\lim_{x→1^+}\frac{2}{3(x−1)^{1/3}}=∞\text{ and } \lim_{x→1^−}\frac{2}{3(x−1)^{1/3}}=−∞.\nonumber \]

Por lo tanto,$f$ tiene una cúspide en$x=1.$

Paso 6: Para determinar la concavidad, calculamos la segunda derivada de$f:$

\[f''(x)=−\dfrac{2}{9}(x−1)^{−4/3}=\dfrac{−2}{9(x−1)^{4/3}}. \nonumber \]

Encontramos que$f''(x)$ está definido para todos$x$, pero es indefinido cuando$x=1$. Por lo tanto, divida el intervalo$(−∞,∞)$ en los intervalos más pequeños$(−∞,1)$ y$(1,∞)$, y elija puntos de prueba para evaluar el signo de$f''(x)$ en cada uno de estos intervalos. Como hicimos antes, vamos$x=0$ y$x=2$ ser puntos de prueba como se muestra en la siguiente tabla.

Intervalo	Punto de prueba	Signo de$f''(x)=\dfrac{−2}{9(x−1)^{4/3}}$	Conclusión
$(−∞,1)$	$x=0$	\ (f "(x) =\ dfrac {−2} {9 (x−1) ^ {4/3}}\)” style="text-align:center; ">$−/+=−$	$f$es cóncavo hacia abajo
$(1,∞)$	$x=2$	\ (f "(x) =\ dfrac {−2} {9 (x−1) ^ {4/3}}\)” style="text-align:center; ">$−/+=−$	$f$es cóncavo hacia abajo

De esta tabla, concluimos que$f$ es cóncavo hacia abajo en todas partes. Combinando toda esta información, llegamos a la siguiente gráfica para$f$.

$Se grafica la función f (x) = (x − 1) 2/3. Toca el eje x en x = 1, donde llega a algo así como una punta afilada y luego se ensancha a cada lado.$

Ejercicio$\PageIndex{11}$

Considera la función$f(x)=5−x^{2/3}$. Determinar el punto en la gráfica donde se encuentra una cúspide. Determinar el comportamiento final de$f$.

Pista: Una función$f$ tiene una cúspide en un punto$a$ si$f(a)$ existe, no$f'(a)$ está definida, uno de los límites unilaterales a partir$x→a$ de$f'(x)$ es$+∞$, y el otro límite unilateral es$−∞.$

Contestar: La función$f$ tiene una cúspide en$(0,5)$, desde$\displaystyle \lim_{x→0^−}f′(x)=∞$ y$\displaystyle \lim_{x→0^+}f′(x)=−∞$. Para el comportamiento final,$\displaystyle \lim_{x→±∞}f(x)=−∞.$

Conceptos clave

El límite de$f(x)$ es$L$ como$x→∞$ (o como$x→−∞)$ si los valores$f(x)$ se acercaran arbitrariamente a$L$ como$x$ se vuelve suficientemente grande.
El límite de$f(x)$ es$∞$ como$x→∞$ si$f(x)$ se volviera arbitrariamente grande como$x$ se vuelve suficientemente grande. El límite de$f(x)$ es$−∞$ como$x→∞$ si$f(x)<0$ y$|f(x)|$ se vuelve arbitrariamente grande como$x$ se vuelve suficientemente grande. Podemos definir el límite de$f(x)$ como$x$ enfoques de$−∞$ manera similar.
Para una función polinómica$p(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0,$ donde$a_n≠0$, el comportamiento final está determinado por el término principal$a_nx^n$. Si$n≠0, p(x)$ se acerca$∞$ o$−∞$ en cada extremo.
Para una función racional,$f(x)=\dfrac{p(x)}{q(x),}$ el comportamiento final está determinado por la relación entre el grado de$p$ y el grado de$q$. Si el grado de$p$ es menor que el grado de$q$, la línea$y=0$ es una asíntota horizontal para$f$. Si el grado de$p$ es igual al grado de$q$, entonces la línea$y=\dfrac{a_n}{b_n}$ es una asíntota horizontal, donde$a_n$ y$b_n$ son los coeficientes principales de$p$ y$q$, respectivamente. Si el grado de$p$ es mayor que el grado de$q$, entonces se$f$ acerca$∞$ o$−∞$ en cada extremo.

Glosario

comportamiento final: el comportamiento de una función como$x→∞$ y$x→−∞$

asíntota horizontal: si$\displaystyle \lim_{x→∞}f(x)=L$ o$\displaystyle \lim_{x→−∞}f(x)=L$, entonces$y=L$ es una asíntota horizontal de$f$

límite infinito en el infinito: una función que se vuelve arbitrariamente grande a medida que$x$ se vuelve grande

límite al infinito: una función que se acerca a un valor límite a$L$ medida que$x$ se vuelve grande

asíntota oblicua: la línea$y=mx+b$ si$f(x)$ se acerca a ella como$x→∞$ o$ x→−∞$

Intervalo	Punto de prueba	Signo de Derivada\(f'(x)=3x^2−3=3(x−1)(x+1)\)	Conclusión
\((−∞,−1)\)	\(x=−2\)	\ (f' (x) =3x^2−3=3 (x−1) (x+1)\)” style="text-align:center; ">\((+)(−)(−)=+\)	\(f\)está aumentando
\((−1,1)\)	\(x=0\)	\ (f' (x) =3x^2−3=3 (x−1) (x+1)\)” style="text-align:center; ">\((+)(−)(+)=−\)	\(f\)decreciente
\((1,∞)\)	\(x=2\)	\ (f' (x) =3x^2−3=3 (x−1) (x+1)\)” style="text-align:center; ">\((+)(+)(+)=+\)	\(f\)está aumentando

Intervalo	Punto de prueba	Signo de\(f''(x)=6x\)	Conclusión
\((−∞,0)\)	\(x=−1\)	\ (f "(x) =6x\)” style="text-align:center; ">\(−\)	\(f\)es cóncavo hacia abajo.
\((0,∞)\)	\(x=1\)	\ (f "(x) =6x\)” style="text-align:center; ">\(+\)	\(f\)es cóncavo hacia arriba.

Intervalo	Punto de prueba	Signo de\(f′(x)=\frac{2x}{(1−x^2)^2}\)	Conclusión
\((−∞,−1)\)	\(x=−2\)	\ (f′ (x) =\ frac {2x} {(1−x^2) ^2}\)” style="text-align:center; ">\(−/+=−\)	\(f\)está disminuyendo.
\((−1,0)\)	\(x=−1/2\)	\ (f′ (x) =\ frac {2x} {(1−x^2) ^2}\)” style="text-align:center; ">\(−/+=−\)	\(f\)está disminuyendo.
\((0,1)\)	\(x=1/2\)	\ (f′ (x) =\ frac {2x} {(1−x^2) ^2}\)” style="text-align:center; ">\(+/+=+\)	\(f\)va en aumento.
\((1,∞)\)	\(x=2\)	\ (f′ (x) =\ frac {2x} {(1−x^2) ^2}\)” style="text-align:center; ">\(+/+=+\)	\(f\)va en aumento.

Intervalo	Punto de prueba	Signo de\(f''(x)=\frac{6x^2+2}{(1−x^2)^3}\)	Conclusión
\((−∞,−1)\)	\(x=−2\)	\ (f "(x) =\ frac {6x^2+2} {(1−x^2) ^3}\)” style="text-align:center; ">\(+/−=−\)	\(f\)es cóncavo hacia abajo.
\((−1,1)\)	\(x=0\)	\ (f "(x) =\ frac {6x^2+2} {(1−x^2) ^3}\)” style="text-align:center; ">\(+/+=+\)	\(f\)es cóncavo hacia arriba
\((1,∞)\)	\(x=2\)	\ (f "(x) =\ frac {6x^2+2} {(1−x^2) ^3}\)” style="text-align:center; ">\(+/−=−\)	\(f\)es cóncavo hacia abajo.

Intervalo	Punto de prueba	Signo de\(f'(x)=\dfrac{x^2−2x}{(x−1)^2}\)	Conclusión
\((−∞,0)\)	\(x=−1\)	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)” datos-valign="top"> (−) (−) /+=+	\(f\)va en aumento.
\((0,1)\)	\(x=1/2\)	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)” datos-valign="top"> (+) (−) /+=−	\(f\)está disminuyendo.
\((1,2)\)	\(x=3/2\)	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)” datos-valign="top"> (+) (−) /+=−	\(f\)está disminuyendo.
\((2,∞)\)	\(x=3\)	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)” valign="top"> (+) (+) /+=+	\(f\)va en aumento.

Search

Definición: Límite al Infinito (Informal)

Definición: Asíntota horizontal

Ejemplo\(\PageIndex{1}\): Computing Limits at Infinity

Ejercicio\(\PageIndex{1}\)

Definición: Límite Infinito en el Infinito (Informal)

Definición: Límite al infinito (Formal)

Ejemplo\(\PageIndex{2}\):

Ejercicio\(\PageIndex{2}\)

Definición: Límite infinito en el infinito (Formal)

Ejemplo\(\PageIndex{3}\)

Ejercicio\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\): Limits at Infinity for Power Functions

Ejercicio\(\PageIndex{4}\)

Ejemplo\(\PageIndex{5}\): Determining End Behavior for Rational Functions

Ejercicio\(\PageIndex{5}\)

Ejemplo\(\PageIndex{6}\): Determining End Behavior for a Function Involving a Radical

Ejercicio\(\PageIndex{6}\)

Ejemplo\(\PageIndex{7}\): Determining End Behavior for a Transcendental Function

Ejercicio\(\PageIndex{7}\)

Estrategia de resolución de problemas: dibujo de la gráfica de una función

Ejemplo\(\PageIndex{8}\): Sketching a Graph of a Polynomial

Ejercicio\(\PageIndex{8}\)

Ejemplo\(\PageIndex{9}\): Sketching a Rational Function

Ejercicio\(\PageIndex{9}\)

Ejemplo\(\PageIndex{10}\): Sketching a Rational Function with an Oblique Asymptote

Ejercicio\(\PageIndex{10}\)

Ejemplo\(\PageIndex{11}\): Sketching the Graph of a Function with a Cusp

Ejercicio\(\PageIndex{11}\)

\(x\)	10	100	1,000	10,000
\(2+\frac{1}{x}\)	2.1	2.01	2.001	2.0001
\(x\)	−10	−100	−1000	−10,000
\(2+\frac{1}{x}\)	1.9	1.99	1.999	1.9999

\(x\)	10	20	50	100	1000
\(x^3\)	1000	8000	125,000	1,000,000	1,000,000,000
\(x\)	−10	−20	−50	−100	−1000
\(x^3\)	−1000	−8000	−125.000	−1,000,000	−1,000,000,000

\(x\)	10	100	1000
\(f(x)=5x^3−3x^2+4\)	4704	4,970,004	4,997,000,004
\(g(x)=5x^3\)	5000	5,000,000	5,000,000,000
\(x\)	−10	−100	−000
\(f(x)=5x^3−3x^2+4\)	−5296	−5.029.996	−5,002,999,996
\(g(x)=5x^3\)	−5000	−5,000,000	−5,000,000,000

Intervalo	Punto de prueba	Signo de\(f''(x)=\dfrac{2}{(x−1)^3}\)	Conclusión
\((−∞,1)\)	\(x=0\)	\ (f "(x) =\ dfrac {2} {(x−1) ^3}\)” style="text-align:center; ">\(+/−=−\)	\(f\)es cóncavo hacia abajo.
\((1,∞)\)	\(x=2\)	\ (f "(x) =\ dfrac {2} {(x−1) ^3}\)” style="text-align:center; ">\(+/+=+\)	\(f\)es cóncavo hacia arriba