2.3: Límites de las Funciones Polinómicas y Racionales
- Page ID
- 105918
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Funciones polinómicas
Recordemos que una función f (x) polinomio función si satisface:
\[f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{2} x^{2}+a_{1} x+a_{0}\]
para todos x, donde n es un entero no negativo y\(a_0\),\(a_1\),\(a_2\),...,\(a_n\) son coeficientes constantes.
Como actualización, use las propiedades limit para encontrar el límite de (x 2 −3x+4) como x→20, es decir, el límite a medida que x se acerca a un valor particular.
La función es un polinomio, un trinomio cuadrático que se grafica a continuación, y puede tratarse como la suma de tres funciones. Esto significa que podemos utilizar la regla “el límite de la suma es la suma de los límites” en la determinación del límite.
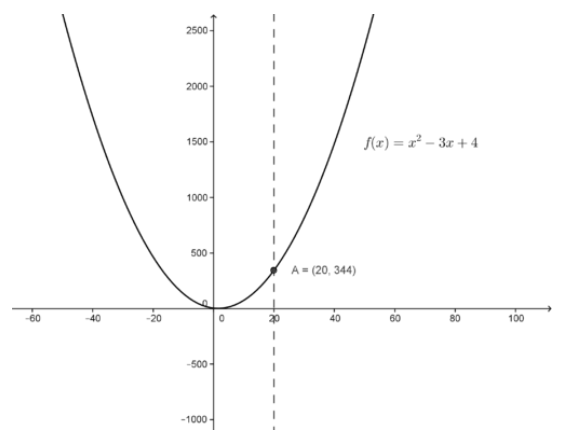
CC BY-NC-SA
Ya que, el polinomio puede tratarse como la suma de tres funciones, podemos utilizar la propiedad “el límite de la suma es la suma de los límites” en la determinación del límite.
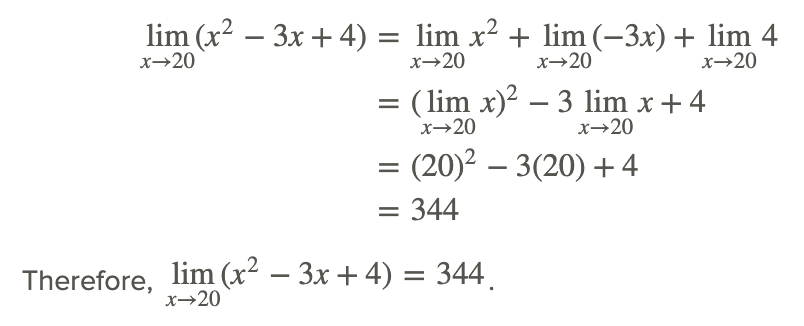
Obsérvese que el valor de este límite podría haberse encontrado por sustitución directa de x=1 en la función polinómica.
Ahora, encuentra
\[\lim _{x \rightarrow \infty}\left(x^{2}-3 x+4\right)\]
es decir, el límite a medida que x se acerca al infinito. Esto es mirar al final del comportamiento.
El polinomio puede ser tratado como el producto de dos funciones. Esto significa que podemos utilizar la regla “el límite del producto de funciones es producto de los límites de cada función” en la determinación del límite.
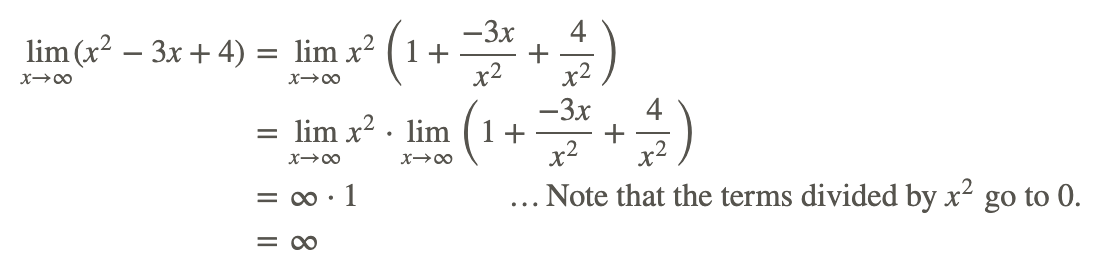
Por lo tanto,
\[\lim _{x \rightarrow \infty}\left(x^{2}-3 x+4\right)=\infty.\]
Una evaluación similar muestra que
\[\lim _{x \rightarrow-\infty}\left(x^{2}-3 x+4\right)=\infty.\]
Este comportamiento representa el hecho de que el comportamiento final de los polinomios va como el término con el grado más alto, y los valores crecen sin límite.
Los resultados de estos dos ejemplos pueden generalizarse a las siguientes propiedades:
Dada la función polinómica f (x) =p (x):
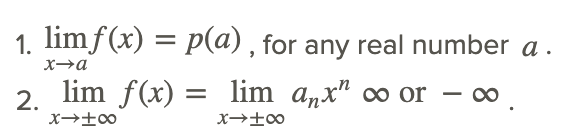
Funciones racionales
Ahora consideremos los límites de las funciones racionales. Una función racional es la relación de dos polinomios. En el caso de una sola variable, x, una función se denomina función racional si y solo si se puede escribir en la forma:
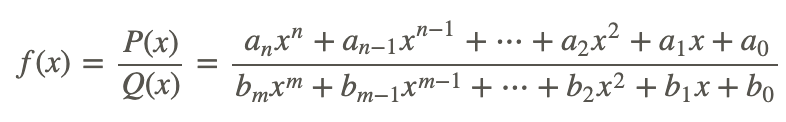
donde P (x) y Q (x) son funciones polinómicas en x y Q (x) no es cero. El dominio de f es el conjunto de todos los valores de x para los cuales el denominador Q (x) no es cero.
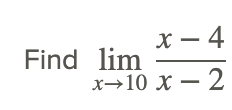
La función se muestra en la gráfica a continuación.
CC BY-NC-SA
Observamos primero que el denominador de la función racional no es cero en el valor x=10. Por lo tanto, la regla del cociente se puede utilizar para iniciar la evaluación de la función de la siguiente manera:
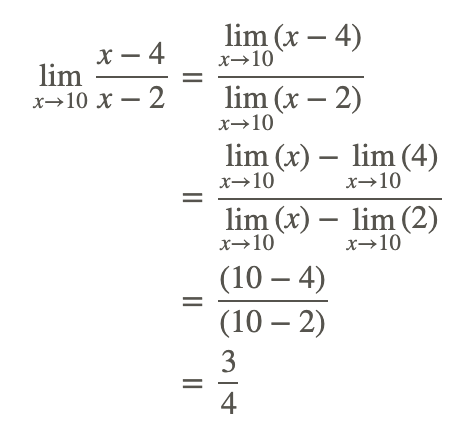
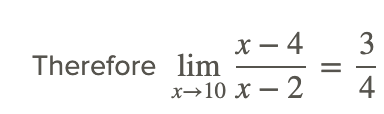
Obsérvese que debido a que el denominador no es igual a 0 en x=10, el límite podría haberse encontrado por sustitución directa de x=10 en la función racional.
Ahora, encuentra el comportamiento final de esa misma función, es decir, encontrar
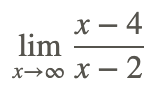
Los siguientes pasos se utilizan para evaluar el límite a medida que x se acerca al infinito.
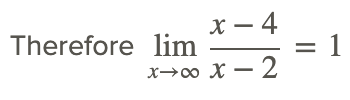
Los problemas anteriores ilustran la evaluación del límite de una función racional a un valor de x para el cual el denominador no es igual a 0. A veces encontrar el límite de una función racional f (x) en algún x=a puede implicar más trabajo que solo sustitución directa porque el denominador es igual a cero en x=a. ¿Y si el denominador es igual a 0?
Observe que la función aquí es indeterminada en x=2, por lo que la sustitución directa no funciona. Sin embargo, en este caso es posible eliminar el cero en el denominador factorizando el numerador y cancelando el factor (x−2) tanto del numerador como del denominador.
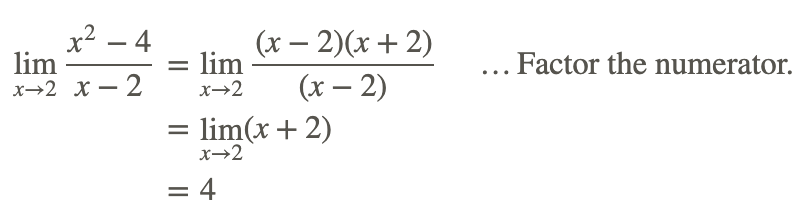
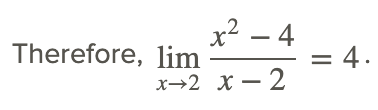
El factorización del numerador mostrado anteriormente, y luego cancelar cualquier factor común en el denominador, es una técnica común utilizada para encontrar los límites de las funciones racionales en puntos donde el denominador es 0. Siempre verifique para ver si la función se puede simplificar para eliminar el cero en el denominador, especialmente cancelando común un factor que elimina una discontinuidad.
Ahora, encuentra
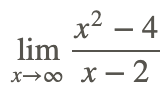
Observamos el comportamiento final de la función como x va al infinito de la siguiente manera:
Por lo tanto,
\[\lim _{x \rightarrow \infty} \frac{x^{2}-4}{x-2}=\infty\]
El comportamiento final a medida que x va a −∞ se puede determinar mediante un enfoque similar, y se encuentra que es −∞.
Definición del límite de las funciones racionales
Para la función racional f (x) = p (x)/q (x) y cualquier número real a,
\[\lim _{x \rightarrow a} f(x)=\frac{p(a)}{q(a)}\) if \(q(a) \neq 0\]
Si q (a) =0, entonces la función puede tener o no un límite.
Para la función racional
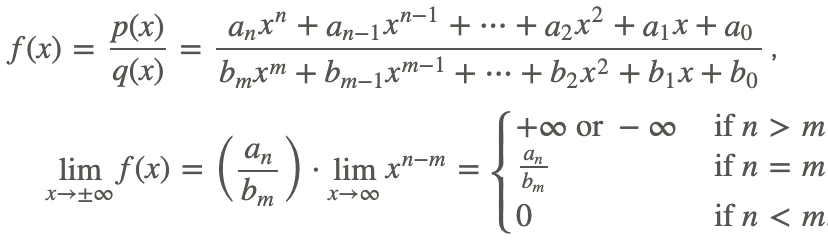
Ejemplos
Ejemplo 1
Anteriormente, se le preguntó sobre las respectivas dificultades de encontrar el límite de las funciones polinomiales y racionales. Encontrar el límite de una función polinómica es relativamente fácil porque una función polinómica puede evaluarse en cualquier valor de la variable independiente para que el límite en un valor específico pueda ser evaluado por sustitución directa. El límite a medida que la variable independiente va a ±∞ es solo ±∞ dependiendo de si el grado del polinomio es par o impar.
Evaluar el límite de una función racional puede ser más difícil porque la sustitución directa puede conducir a una forma indefinida o indeterminada que requiere un enfoque diferente, y el límite como variable independiente va a ±∞ depende de cuál es mayor, el grado del polinomio numerador o el grado de polinomio denominador.
Ejemplo 2
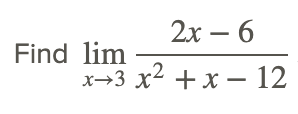
El numerador y el denominador son iguales a cero en x=3, pero hay un factor común x−3 que se puede eliminar (es decir, podemos simplificar la función racional):
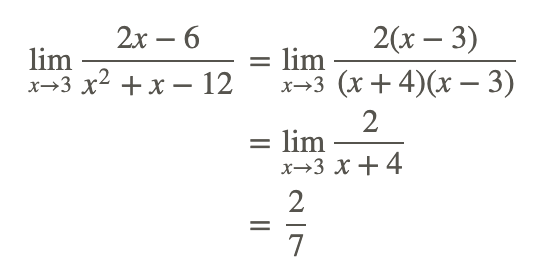
Ejemplo 3
Encuentra
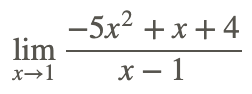
para encontrar
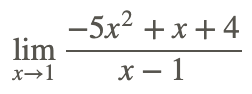
... Comience por factorizar el numerador
Como tenemos (x−1) tanto en el numerador como en el denominador, sabemos que la función original es igual a solo −5x−4 excepto donde no está definida (1).
Por lo tanto, cuanto más nos acercamos a la entrada 1, más nos acercamos al mismo valor, ya sea del lado + o -.
Para encontrar el valor, solo resuelve
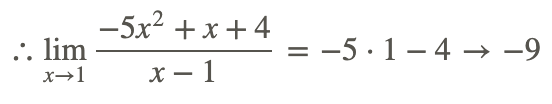
Ejemplo 4
Encuentra
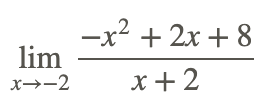
para encontrar
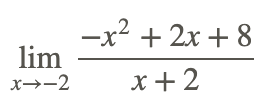
... Comience por factorizar el numerador
Como tenemos (x+2) tanto en el numerador como en el denominador, sabemos que la función original es igual a solo −x−4
Por lo tanto, cuanto más nos acercamos a sustituir -2, más nos acercamos al mismo valor de salida, ya sea desde el lado + o -.
Para encontrar el valor, solo resuelve −x−4 para x=−2
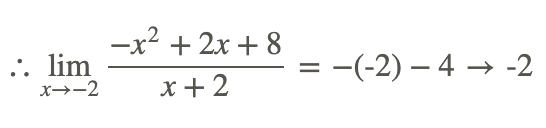
Revisar
Resolver los siguientes límites de función racional.
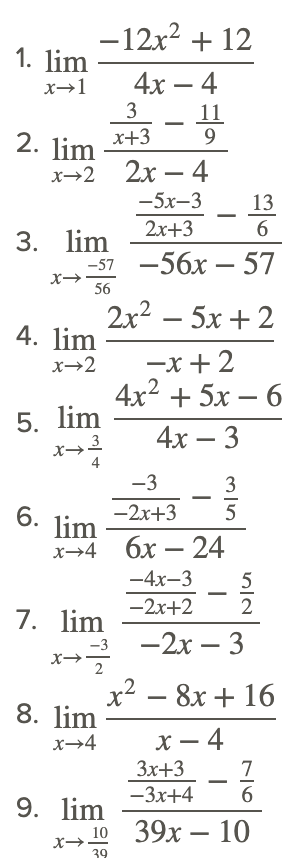
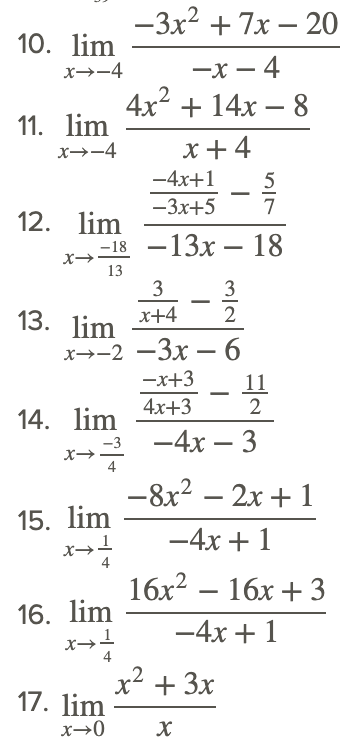
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.5.
El vocabulario
| Término | Definición |
|---|---|
| discontinuo | Una función es discontinua si la función presenta roturas o agujeros cuando se grafica. |
| límite | Un límite es el valor que la salida de una función se acerca a medida que la entrada de la función se acerca a un valor dado. |
| Función polinómica | Una función polinómica es una función definida por una expresión con al menos un término algebraico. |
| Función Racional | Una función racional es cualquier función que pueda escribirse como la relación de dos funciones polinómicas. |
Recursos adicionales
PLIX: Juega, aprende, interactúa, explora - Evaluando los límites de las funciones racionales
Video: Ejemplos de límite
Práctica: Límites de funciones polinomiales y racionales
Mundo real: Webslingers