2.4: Límites trigonométricos básicos

Las funciones trigonométricas pueden ser un componente de una expresión y, por lo tanto, estar sujetas a un proceso límite. ¿Cree que la naturaleza periódica de estas funciones, y el rango limitado o infinito de funciones trigonométricas individuales dificultarían la evaluación de los límites que involucran estas funciones?

---

Límites con funciones trigonométricas

Las reglas de límite presentadas en conceptos anteriores ofrecen algunas, pero no todas, de las herramientas para evaluar límites que involucran funciones trigonométricas.

Encontremos los siguientes límites:

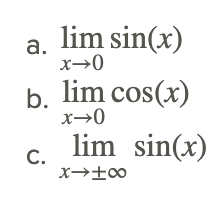
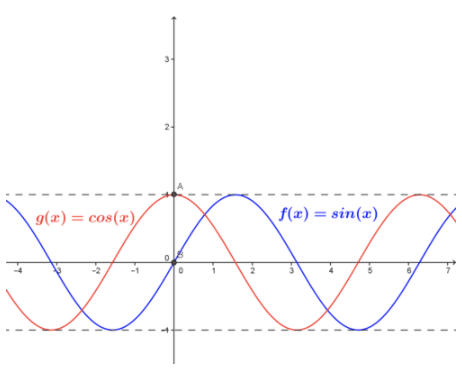
Podemos encontrar estos límites evaluando la función a medida que x se acerca a 0 a la izquierda y a la derecha, es decir, evaluando los dos límites unilaterales. A continuación se muestran los valores de gráficos y tablas.

CC BY-NC-SA

x (rad)	-0.001	-0.0001	0	0.0001	0.001
sin (x)	-0.001	-0.0001	0	0.0001	0.001
cos (x)	0.999	0.9999	1	0.9999	0.999

La inspección de la gráfica a continuación, y tabla de valores en las proximidades de x=0, indica que:

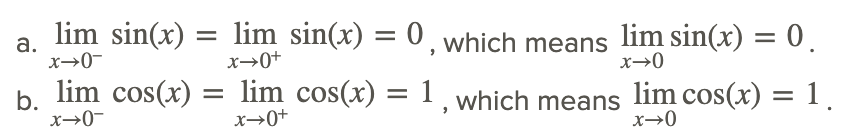
Tenga en cuenta que los límites se pueden encontrar usando sustitución directa.

3. Debido a que sin (x) es una función periódica, a medida que x se hace más grande (más pequeño) y más grande (más pequeño), su valor oscilará entre 1 y -1, y nunca se asentará en un solo valor. Por lo tanto, podemos decir que eso
   
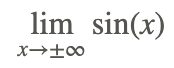
   no existe.

Podemos generalizar y ampliar los hallazgos anteriores y presentar las siguientes propiedades:

Propiedades de límite para funciones trigonométricas básicas

• Límite como x→a para cualquier a real:

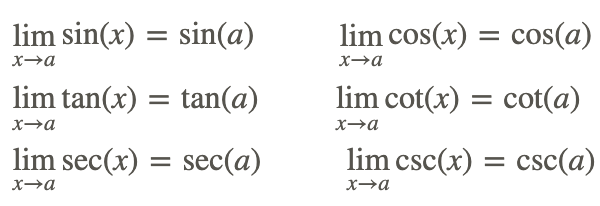
• Límite como x→±∞:

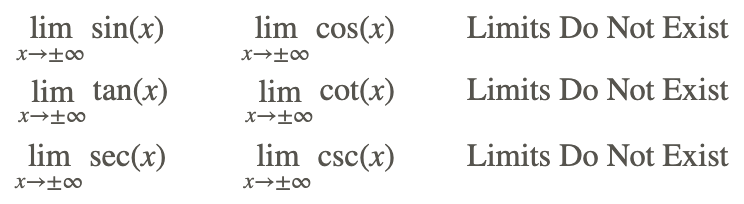
Vamos a encontrar

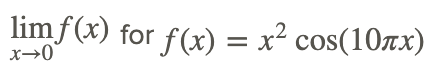
A continuación se muestra la gráfica de la función.

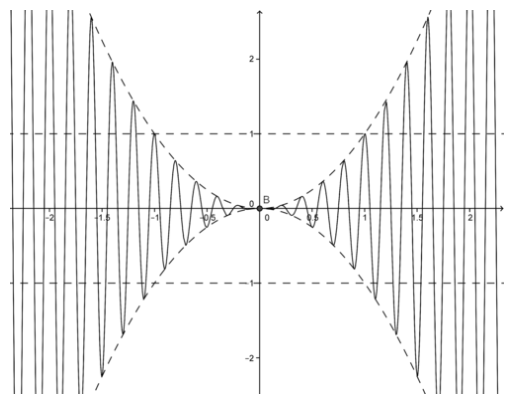
CC BY-NC-SA

Como sabemos que existen el límite de x ² y cos (x), podemos encontrar el límite de esta función aplicando la Regla de Producto, o sustitución directa:

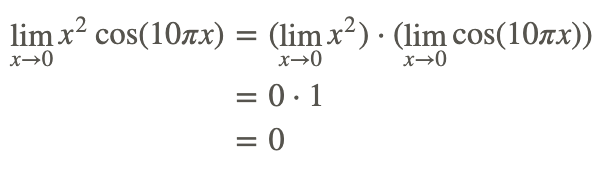
Por lo tanto,

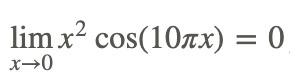
Además, a partir de la gráfica de la función, observamos que la función está delimitada por las gráficas de x2 y −x2, que ambas son 0 en x=0. Tiene sentido que el límite de la función original sea 0.

El teorema del apretón

Esta característica, que el límite de una función puede resultar de que la función esté delimitada o apretada por otras dos funciones, es la base del Teorema de Squeeze. El Teorema de Squeeze (también conocido como el Teorema Sandwich) establece:

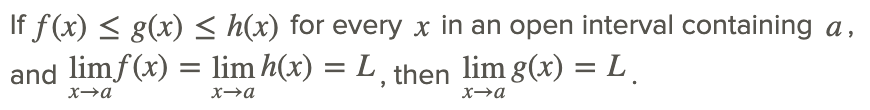
Es decir, si podemos encontrar límites para una función que tenga el mismo límite, entonces el límite de la función que vincularon debe tener el mismo límite. Tenga en cuenta que a y L pueden ser cualquier constante o incluso ∞ o −∞.

Uno de los límites trigonométricos importantes que se pueden probar, en parte, utilizando el Teorema de Squeeze es:

Es decir, si podemos encontrar límites para una función que tenga el mismo límite, entonces el límite de la función que vincularon debe tener el mismo límite. Tenga en cuenta que a y L pueden ser cualquier constante o incluso ∞ o −∞.

Uno de los límites trigonométricos importantes que se pueden probar, en parte, utilizando el Teorema de Squeeze es:

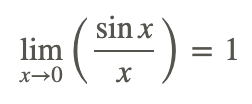
donde x está en medida de radianes.

Otro límite trigonométrico importante es

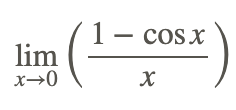
La sustitución directa no puede ser utilizada para evaluar el límite porque produce la forma indeterminada ⁰/₀. En cambio, transforma el problema a una forma diferente y resuelve.

---

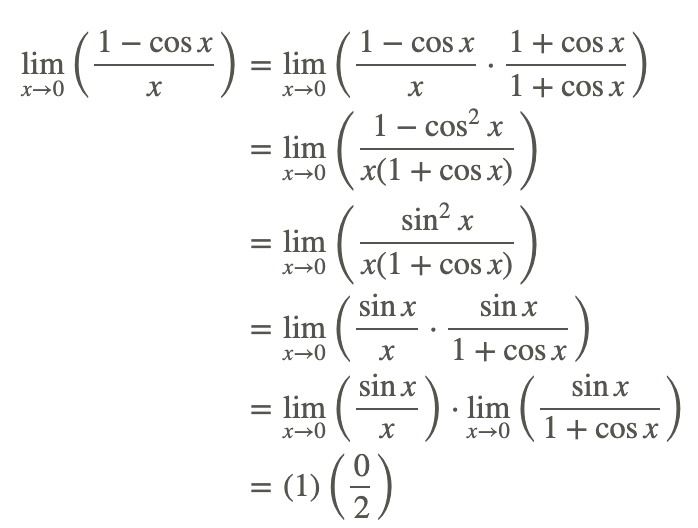
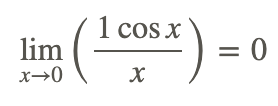
Ejemplos

Ejemplo 1

Anteriormente, se le preguntó si la naturaleza periódica de las funciones trigonométricas y el rango limitado o infinito de funciones trigonométricas individuales dificultan la evaluación de límites que involucran funciones trigonométricas.

Como puedes imaginar y haber visto en este concepto, algunos límites que involucran funciones trigonométricas pueden ser fácilmente evaluados por sustitución directa, y algunos evolucionan mucho trabajo para cambiar de forma de una forma indeterminada o indefinida. Determinar el comportamiento final de una expresión que involucra una función trigonométrica también puede ser difícil, y requerir la aplicación de principios como el Teorema de Squeeze para obtener un resultado. ¡No es una respuesta fácil!

Ejemplo 2

Encuentra

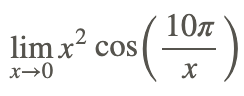
La sustitución directa no se puede usar para evaluar el límite porque ^10π/_x no está definido cuando x=0.

Sin embargo, el Teorema Squeeze se puede utilizar de la siguiente manera:

1. Sabemos que el coseno se mantiene entre -1 y 1, entonces

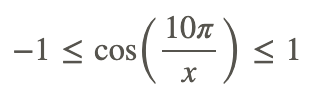
para cualquier x en el dominio de la función (es decir, cualquier x≠ 0).

2. Dado que x ² es siempre no negativo, podemos multiplicar la desigualdad anterior por x ²:

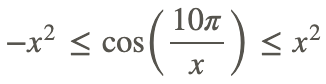
3. La función original está limitada por x ² y −x ² y

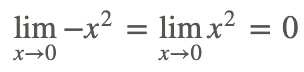
4. Por lo tanto, por el Teorema Squeeze:

---

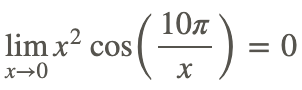
Revisar

---

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.7.

---

El vocabulario

Término	Definición
indeterminado	En matemáticas, una expresión es indeterminada si no se define con precisión. Hay siete formas indeterminadas: 00,0∞, ∞, ∞ −∞, ∞ −∞, ∞, ∞ 0, y 1^\ infty.
límite	Un límite es el valor que la salida de una función se acerca a medida que la entrada de la función se acerca a un valor dado.
teorema de squeeze	El teorema squeeze (también conocido como teorema sandwich) se utiliza para encontrar el límite de una función delimitándola entre otras dos funciones que cada una tiene el mismo límite.

---

Recursos adicionales

PLIX: Juega, aprende, interactúa, explora - Evaluando los límites del bronceado (x)

Video: Determinación de límites que involucran funciones trigonométricas

Práctica: Límites trigonométricos básicos

Mundo real: Volaré lejos